分数槽切向磁路永磁电机齿顶漏磁分析
赵 佳,张树刚
(呼伦贝尔职业技术学院 机电工程系,呼伦贝尔 021000)
0 引 言
分数槽切向磁路永磁电机有两个永磁体截面对气隙提供每极磁通,可提高气隙磁密[1],非常适用于矿山、水泥、钢厂、金属冶炼等需要低速大转矩的驱动场合。电机的齿顶漏磁对电机有不利影响[2],严重的齿顶漏磁会降低永磁材料的利用率,进而降低电机的平均电磁转矩,当电机旋转时还会引起与各相绕组相交链的磁通发生周期性波动,使电机绕组感生的反电动势发生波动,产生纹波转矩,从而影响系统的控制精度。因此,有必要研究电机的齿顶漏磁,然而在现有研究中[3-4],少有适用于分数槽切向磁路永磁电机齿顶漏磁的计算方法。
本文对极靴表面磁密分布进行等效划分,计算一个极下齿顶漏磁导,引入单元电机齿顶漏磁概念,得到一个单元电机下各个磁极的齿顶漏磁,并分析了定子齿顶与定子槽口宽度的比值对单元电机齿顶漏磁的影响。最后运用有限元法对30极72槽切向磁路永磁电机齿顶漏磁进行分析,验证了研究内容的准确性。
1 分数槽电机齿顶漏磁通特性分析
分数槽电机各个极下的齿顶漏磁呈现一定的周期性[5]。针对这种周期性,本文引入单元电机齿顶漏磁概念。每台电机都可分为若干单元电机,每个单元电机由沿旋转方向相邻且齿顶漏磁各不相同的磁极和对应的定子组成,如图1所示。
单元电机齿顶漏磁是其包含的所有磁极的齿顶漏磁之和。分数槽电机的齿顶漏磁以单元电机为变化周期,单元电机之间齿顶漏磁完全相同。单元电机个数是电机定子槽数与极数的最大公约数(GCD)。
2 齿顶漏磁计算方法
2.1 一个极下的齿顶漏磁通
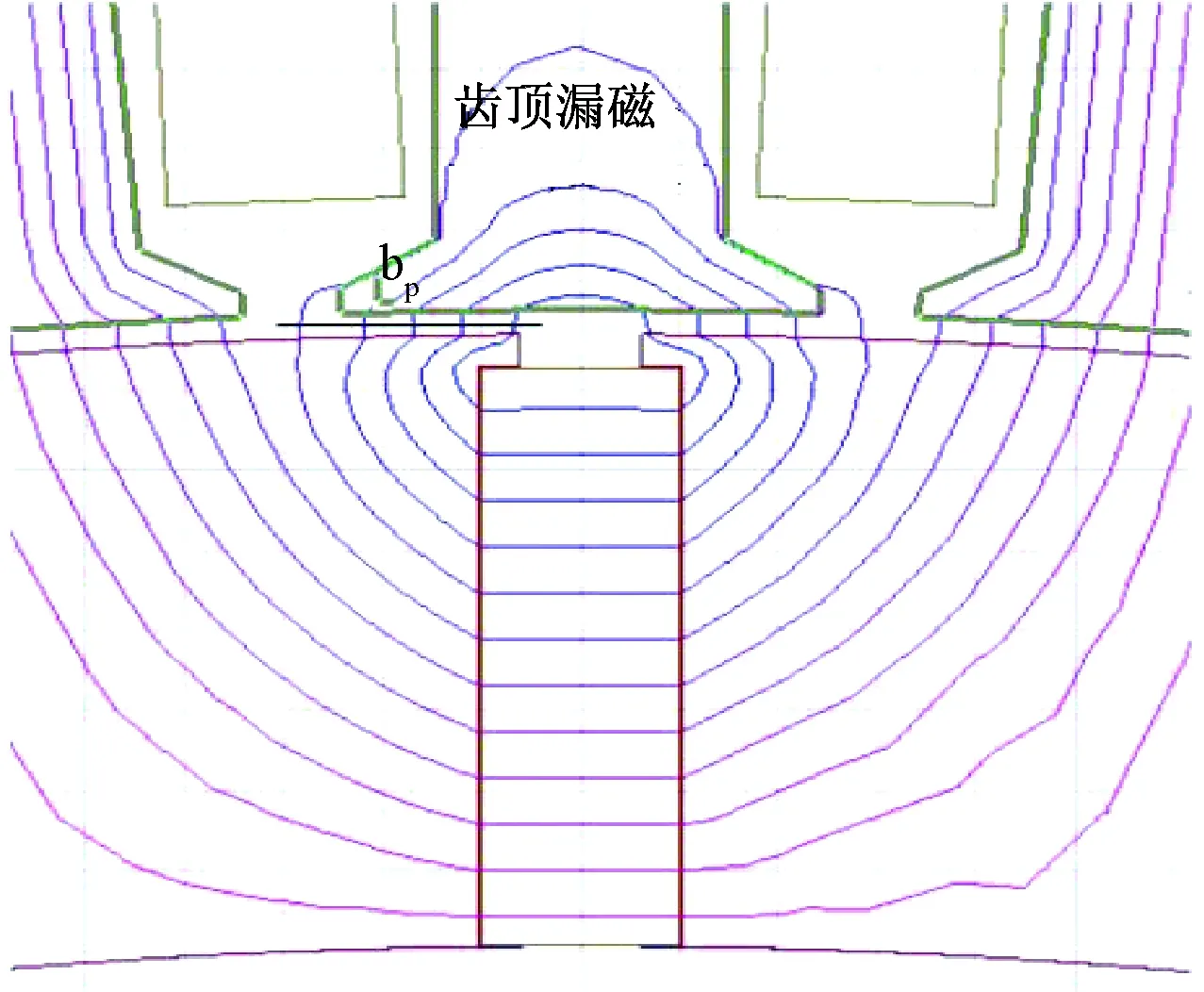
在切向磁路永磁电机中,齿顶漏磁通由永磁体发出,经转子铁心、气隙进入定子齿顶,再经气隙和转子铁心回到永磁体[6],整个过程不与绕组发生交链。考虑气隙的边缘效应,对一个极下齿顶漏磁提出如下简化模型:在定转子铁心相对部分,磁密分布相同,在定转子开槽部分,磁密分布各不相同[7]。
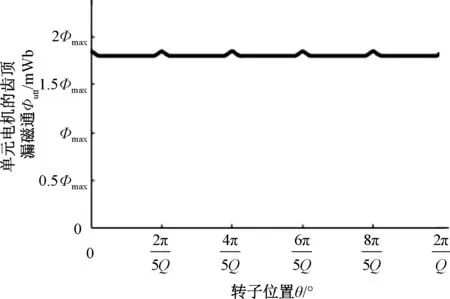
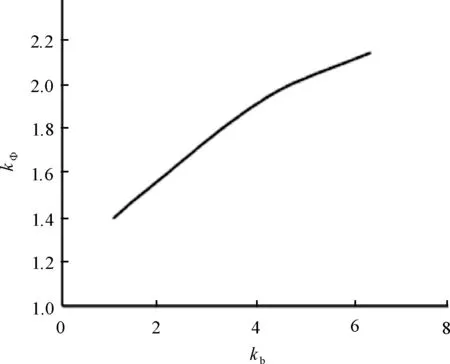
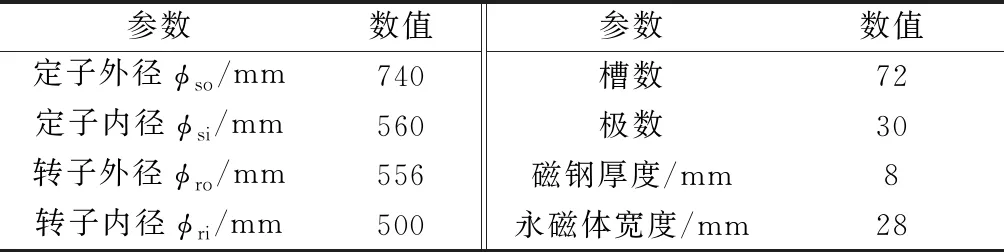
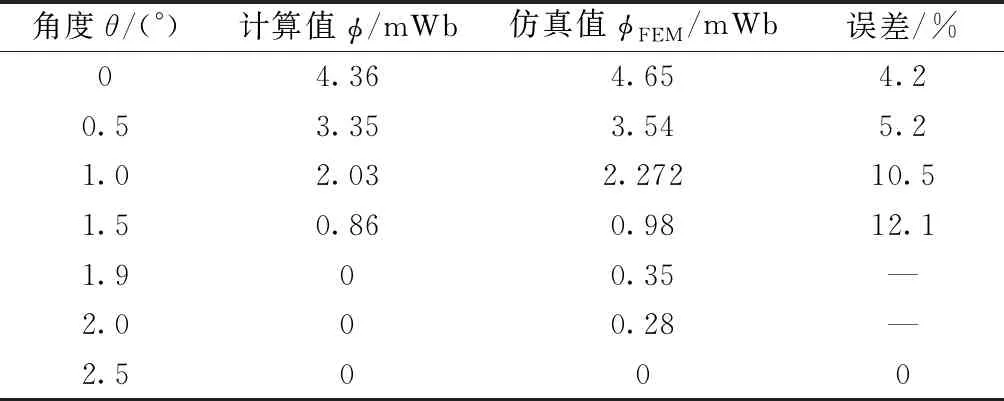
分数槽切向磁路电机一个极下结构图,如图2所示。图2中,b1和b2分别是定、转子槽口宽度,bx是定子齿顶宽度,bm为永磁体激磁方向厚度,δ为气隙长度。对于设计合理的切向磁路永磁电机,记电机齿距为τ,则有2δ 图2 分数槽切向磁路电机一个极下结构图 对定、转子开槽处极靴磁密做等效处理,将其等效为磁密大小为Bav、所占宽度为kδδ的等效磁密,其余部分的磁密为0。kδ为气隙系数,是因定、转子开槽而使齿顶漏磁通路径宽度增加的系数,kδ>0。 在切向磁路永磁电机中,永磁体提供的磁通一部分进入气隙[8],另一部分从转子转轴处回到永磁体。提供磁通进入气隙部分的永磁体宽度bm近似等于极靴宽度的1/2,参与到齿顶漏磁永磁体的宽度与参与齿顶漏磁的极靴宽度可认为相同。齿顶漏磁通从r侧进入定子齿顶的路径宽度bp=(r-b2/2+2kδδ),则参与齿顶漏磁的永磁体宽度也是bp。 为提高计算速度,假设定转子铁心不饱和[9],磁导率为无穷大,且忽略端部的影响[10]。转子q轴轴线与右侧距离最近的定子齿轴线之间的距离记为x(0≤x (1) 式中,a、b、c满足: (2) 同理,可得到永磁体的齿顶漏磁导ΛPM,忽略定转子铁心磁导,整个齿顶漏磁路径的总磁导满足: Λ=Λδ‖ΛPM (3) 磁路总的磁势F由永磁体提供,那么,一个极下的齿顶漏磁通Φtt即可得到: Φtt=FΛ=Hcbm (4) 式中:Hc是永磁体的矫顽力。 由式(1)和式(3)可知,Φtt是关于x的周期函数,表示一个极下齿顶漏磁通Φtt随该磁极从一个定子齿轴线到下一个过程的变化情况。 定子槽数为Q,极数为2p的三相分数槽永磁电机,单元电机个数为GCD,每个单元电机所包含磁极个数为n=2p/GCD。相邻磁极的机械角度ap=π/p,相邻定子齿轴线的机械角度aQ=π/Q。一个单元电机中,记沿着旋转方向的第一个磁极为1号磁极,1号磁极q轴与右侧最近的定子齿轴线间的夹角为θ,0≤θ<2π/Q。在同一时刻,同一单元电机下,第i(1≤i≤GCD)个磁极q轴与右侧距离最近的定子齿轴线的夹角为θi,θi可由式(5)计算: (5) 式中:α=π(n-1)mod(2π/Q)/p+θ,mod()为取余函数。 单元电机齿顶漏磁是单元电机包含的所有磁极齿顶漏磁叠加的结果,因此可得到单元电机在一个周期内齿顶漏磁通Φutt与定转子相对位置θ的曲线关系,如图3所示。可看出,单元电机的齿顶漏磁随θ变化的波动程度较低,可取其平均值作为单元电机齿顶漏磁。 图3 单元电机齿顶漏磁变化曲线 随着定子齿顶宽度bx与槽口宽度b1的比值kb的增加,齿顶漏磁通Φutt与一个极下齿顶漏磁最大值Φmax的比值kΦ也增加。根据提出的模型,得到图4所示的kΦ随kb变化的关系曲线。 图4 切向磁路永磁电机kb与kΦ关系曲线 kb确定后,仅需计算出一个极下最大的齿顶漏磁通,即可得到单元电机的齿顶漏磁,进一步得到整台电机的齿顶漏磁通。 对一台30极72槽切向磁路永磁电机齿顶漏磁进行有限元分析,电机参数如表1所示。 表1 电机参数 一个极下齿顶漏磁二维有限元计算模型如图5所示。有限元计算与数值计算的结果对比如表2和图6所示。 图5 齿顶漏磁二维有限元计算模型 角度θ/(°)计算值ϕ/mWb仿真值ϕFEM/mWb误差/%04.364.654.20.53.353.545.21.02.032.27210.51.50.860.9812.11.900.35—2.000.28—2.5000 图6 齿顶漏磁计算值与有限元结果对比 从表2和图6中可以看出,随着转子q轴与定子齿轴线的夹角θ越接近2.5°,计算误差的比例就越大。这是因为磁场的边缘效应对齿顶漏磁的影响所占的比例越来越大,但误差精度能够满足工程需要。 本文对分数槽切向磁路永磁电机的齿顶漏磁进行分析,建立一个极下齿顶漏磁随定转子相对位置变化的数学模型;引入单元电机齿顶漏磁概念,研究了一个单元电机下各个磁极齿顶漏磁的关系,通过绘制曲线的方法,得到一个单元电机齿顶漏磁随定转子相对位置的变化情况。结合模型发现,定子齿顶与定子槽口的比值和单元电机的平均齿顶漏磁与一个极下最大齿顶漏磁的比值存在联系,并绘制了30极72槽电机下这两个比值的关系,通过查曲线的方法,得到电机的齿顶漏磁。最后,对一台30极72槽切向磁路永磁电机进行理论计算,计算结果和有限元仿真结果验证了该理论的准确性。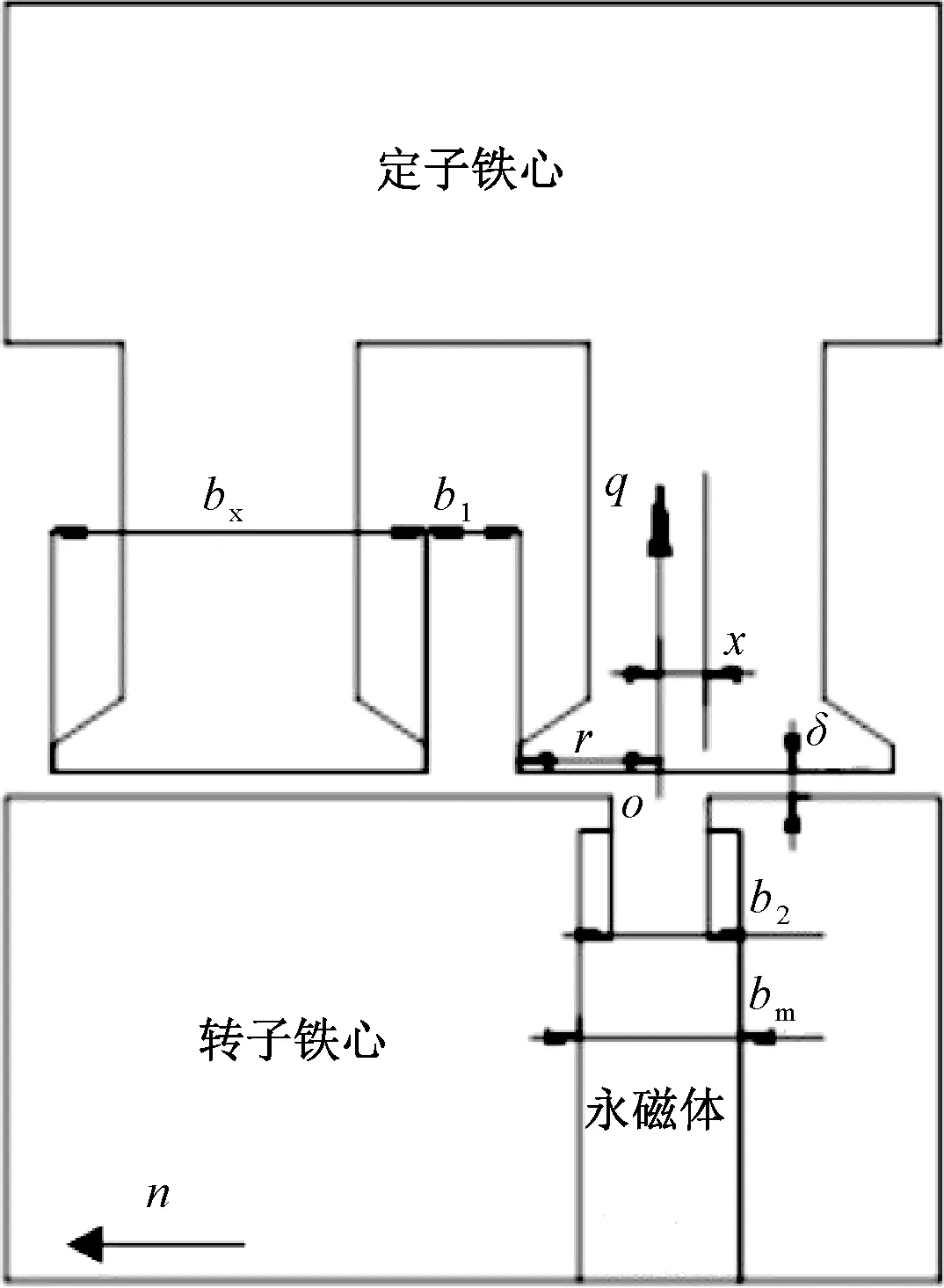
2.2 单元电机齿顶漏磁
3 有限元验证

4 结 语

