语言“转译”
蒋碧云+叶飞
[摘 要]儿童在生活与学习过程中会形成自己的认识,教学中教师可通过各种语言的“转译”,使儿童的这些“自发概念”为同伴所感知、所理解,并使之逐渐科学化。教学是一个独特的、系统的过程,在这一过程中教师应从语言的“转译”入手,让儿童的“自发概念”被激发,生成系统化概念;“自发概念”被唤醒,进入抽象化理解;“自发概念”被进化,开启可视化模式,从而助力儿童“自发概念”科学化。
[关键词]语言转译;自发概念;科学化
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2017)20-0029-03
每个儿童在首次接触一个新知时,都会有自己的数学认识,会从整体上对思维对象进行考察,调动自己的全部知识经验,通过丰富的想象作出假设、猜想或判断,虽然采取了“跳跃式”的思维形式,却常能触及事物的本质,这种认识可称为“自发概念”。儿童会运用自身的语言或者不规范、不完整的数学语言阐述和表达自己的“自发概念”,在此基础上,受变化着的外部条件和内部认知的影响,一些“自发概念”会成功转型为科学概念。作为教师,教学时应顺应儿童的思维特点,从语言的转译入手,让儿童在语言的转译过程中逐步能表达自己的所感、所想及所思,从而催生他们的“自发概念”,为儿童“自发概念”的科学化而助力。
一、儿童语言和文字语言的“转译”:“自发概念”被激发,生成系统化概念
“自发概念”的形成是一瞬间的思维火花,是灵感和顿悟,更是思维过程的高度简化,能触及知识的本质。在儿童语言和文字语言的“转译”中,教师可把儿童“自发概念”中的“火花”放大,并引导他们将其运用于认识新事物,通过将知识系统化,生成科学概念。维科斯基说过:“系统化的萌芽首先是通过儿童与科学概念的接触而进入他的心灵的,然后再被转移到日常概念,从而完全改变了他们的心理结构。”只有当概念成为一个系统的组成部分时,它才能隶属于意识并被有意地控制。概念是否具有系统性,是“自发概念”成功过渡成科学概念的标志。
1.认知积累:语言系统化
2.经验唤醒:比对系统化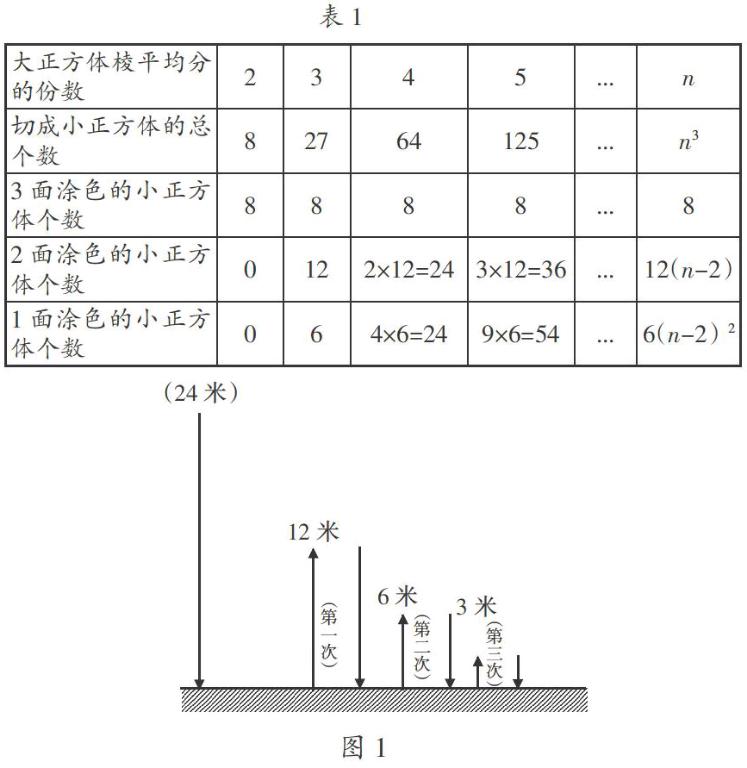
例如,苏教版三年级下册练习中的“巧算法”:在计算一个数与15相乘时,有一种简便的算法——“加半添0”法,如计算24×15,先用24的一半(即12)与24相加,得36;再在36的末尾添0,得360,这个得数即是24×15的积。
学生对于这一简便算法很感兴趣,他们尝试用“加半添0”法计算了26×15、32×15、48×15……发现计算非常简便,随即提出问题:为什么可以这样计算呢?是否跟15这个数有关系?至此,学生已经产生了猜想的“火花”,教师随即放大这一“火花”,并唤醒学生已有的乘法笔算经验。
师:计算到这里你能发现什么?
……
(让学生笔算26×15、32×15、48×15,并与“加半添0”法进行比对。)
师:现在你会解释一个数与15相乘时为什么可以用“加半添0”法计算了吗?
……
经验唤醒和适当比对,使儿童的“自我概念”被激发:“添0”就是乘10,再“加半”就是加上5个这样的数,为了便于计算可以先“加半”再“添0”。当学生学会自我表述这一方法时,“加半添0”的概念才能被他们所接受,进而系统化。
二、符号语言和文字语言的“转译”:“自发概念”被唤醒,进入抽象化理解
符号语言有其独有的精确、简约、深刻的特性,便于学生进行推理、运算和归纳,对一些数学问题的解决有着重要的作用。符号语言有利于促进学生思维的“自由”创造,当学生达到一定程度的认知时,就会自发地给思维对象以恰当的符号,亦可自由地对“思维的自由想象和创造物”进行研究,并用文字语言来进行解释。可以说,给儿童“自发概念”觉醒的一个空间,他会还你一个抽象化的数学世界。
1.顺应思维:唤醒符号表象
例如,学习苏教版四年级下册“乘法分配律”时,学生都会根据等式的特征自主仿写等式,但总结规律时,却表达不清,即使教师出示乘法分配律的文字内容让学生照本宣科,学生也深感困难。这时教师要引导学生说出:“既然这么难说,不如我们用字母符号来表示。”大部分学生都能用字母符号来表示,如“ab+ac=a(b+c)”,還有些学生会用图形来表示。教师追问:“你们怎么想到这样表示呢?”学生:“因为在学习加法的交换律和结合律时,用字母表示很简单。”学生的回答说明了符号化的思想已经在学生的数学世界中“萌芽”了,教师只需唤醒学生记忆中的符号表象,让学生自主进入抽象化的数学世界,再请学生用语言叙述,有据可依,轻而易举就实现了符号语言向文字语言的转译。
2.自主归纳:逐层抽象化
例如,苏教版六年级上册“表面涂色的正方体”是一节数学实践活动课,学生通过参加多样化的活动会生成“自发概念”,并且自然而然地想到用符号语言来归纳这一发现,沟通与长方体相关知识间的联系。对此,教师可设计符合学生认知规律和思维发展的教学活动,让学生在活动中体验,逐层抽象归纳,形成知识的双向建构。具体如下:
(1)分别探究每条棱平均分成2份、3份的正方体表面涂色情况并填表。
(2)重点观察并思考:3面涂色、2面涂色、1面涂色的小正方体分别在什么位置?每种小正方体各有几个?
(3)探究每条棱平均分成4份的正方体表面涂色情况并填表。
(4)猜想每条棱平均分成5份的正方体表面涂色情况并验证猜想。
(5)结合已学的正方体的特征、表面积和体积的计算方法观察表格,你能发现什么?你想怎样表示你的发现?
学生通过自主归纳,得出了如表1所示的结论。
三、文字语言和图形语言的“转译”:“自发概念”被进化,开启可视化模式
科学概念的形成乃是教学与发展的问题,儿童与成人间独特的合作正是科学概念形成的一个重要方面。在数学学习中,“第三次弹起”“便宜”“提高”等数学语言往往会造成儿童阅读的障碍,一些公式的拓展应用也会形成儿童理解的盲区。对此,不妨让学生用自己的“方式”来转译这些词语,从而理解公式的由来,用灵动的数学眼光抓住问题的本质,自由地表达“自发概念”,形成动态化思维,从而催生科学概念的生长。
1.厘清脉络:认知直观化
例如,苏教版三年级上册“解决问题的策略”中的练习:球每次弹起的高度都是下落高度的一半,球从24米高度落下,第三次弹起的高度是多少?
学生大多得出了“6米”这一答案,他们认为只需列式24÷2÷2就可求解,因为从什么高度弹起就从什么高度落下,如第三次弹起和第三次落下的高度是一样的。殊不知,第三次弹起的高度其实是第四次落下的高度。这时教师可鼓励有不一样想法的学生进行汇报,有的学生会用手势表示每次弹起高度是前一次的一半;有的学生则会画图来表示弹起高度是前一次的一半(如图1)。当学生能够逐步把文字语言转译成图形语言,也就说明他们已经厘清了弹起和落下间次数不同的问题。图形语言与其他两种语言相比,更加直观和形象,能够帮助学生建立全局意识,发现事物之间的关系,使学生的“自发概念”逐步科学化。
2.激发图感:推理动态化
例如,苏教版五年级下册“解决问题的策略”中的练习:铅笔架里有10层铅笔,最上层15支,最下层6支,每相邻的两层都相差1支,求一共有多少支铅笔?(铅笔架如图2所示)
学生看到梯形图后很容易就想到可以用(15+6)×10÷2来计算铅笔的总支数,但当教师问“为什么可以这样计算?”时却说不清楚,只是直觉告诉他们可以像计算梯形面积S=(a+b)×h÷2那樣计算。这时,教师可适当提醒:“梯形的面积计算公式是怎样推导出来的?”进而和学生一起回忆公式推导过程,并结合本题进行动态展示(如图3)。
学生进一步归纳:借助图形,我们发现可以把“几个连续自然数相加”转化为“(首项+尾项)×项数÷2”来计算。教师促发学生将“自发概念”产生的符号语言转译成图形语言,又把图形语言转译成通俗易懂的文字语言,进而实现对公式的描述与解释,取得良好的教学效果。在这一过程中,三种语言的综合应用,缺一不可。
叶圣陶先生说过:“教育是农业而不是工业。”意思是教育就像栽培植物那样,要让学生合乎自身规律地自然成长。要让儿童的“自发概念”上升为确切的数学概念,促进儿童数学思维的发展,教师的教学应符合教育教学规律和学生的认知发展规律,以生本课堂为终极目标,以数学知识发生发展的原过程与学生认知过程相融合为本质,以语言的转译为手段,助力儿童的“自发概念”科学化,从而实现师生思维碰撞、智慧交锋与价值共享。
[1] 列夫·维果茨基.思维与语言[M].北京:北京大学出版社,2015.
[2] 余震球.维果茨基教育论著选[M].北京:人民教育出版社,2005.
(责编 黄春香)

