超大型集装箱船参数横摇全面校核与安全评估
马骋远,马宁,王廷昊,顾解忡
1上海交通大学船舶海洋与建筑工程学院,上海200240
2高新船舶与深海开发装备协同创新中心,上海200240
3上海交通大学海洋工程国家重点实验室,上海200240
超大型集装箱船参数横摇全面校核与安全评估
马骋远1,2,马宁2,3,王廷昊1,2,顾解忡2,3
1上海交通大学船舶海洋与建筑工程学院,上海200240
2高新船舶与深海开发装备协同创新中心,上海200240
3上海交通大学海洋工程国家重点实验室,上海200240
[目的]由于超大型集装箱船在波浪中稳性高的变化较为显著,对其参数横摇校核与安全评估要求较高,因此,[方法]基于参数横摇模式,针对在迎浪中航行的某10 000 TEU集装箱船,对其各个装载状况逐一并逐级进行计算。自主开发基于典型弱非线性三自由度模型的数值预报方法,对不满足第2层衡准要求的载况进行时域模拟,并综合考虑航速、波况的影响,全面探索其可能发生参数横摇的工况。[结果]根据衡准结果,得出相应的安全性评估与规避措施:降低重心高度、适当提高航速、尽量避免船舶横摇固有周期约等于2倍遭遇周期等均能有效避免参数横摇的发生。[结论]对10 000 TEU集装箱船进行的参数横摇全面校核评估能够更好地指导超大型集装箱船的总体设计,提高安全水平,具有较高的工程应用及参考价值。
超大型集装箱船;参数横摇;直接计算;安全性评估
0 引 言
国际海事组织(IMO)正在制定包括参数横摇、纯稳性丧失、骑浪/横甩、瘫船稳性和过度加速度这5种稳性失效模式的第2代完整稳性规则[1]。作为第2代完整稳性衡准中的一个重要部分,参数横摇衡准的制定和实施将对船舶性能与设计产生重大影响[2]。对于在纵浪中航行的船舶,当横摇固有周期接近2倍的遭遇周期,且入射波长范围与船长尺度接近时,水线面积会随波浪与船体的相对位置变化发生大幅波动,进而引起初稳性高GM的变化。此时,若船舶横摇阻尼较小,在很小的初始横向扰动下将会出现大幅横摇运动,即发生参数横摇现象[3-5]。这类情况多发生于渔船、客滚船和大型集装箱船[6]。
根据参数横摇的研究成果并考虑工程应用的方便,IMO将衡准划分为了3个层次,即第1层衡准、第2层衡准和直接计算衡准。这3个层次的衡准被设计为从简单的经验公式到采用单自由度非线性力学方法,直至采用较为复杂的三自由度及以上运动数值模拟手段预报参数横摇,依次提高复杂程度并预报精度[7]。在实船设计中,仅当设计方案无法通过低层次衡准时才需要进行更高层次的衡准计算。
大型集装箱船对于参数横摇比较敏感,从对包括APL CHINA号(C11集装箱船)在内的若干实船事故的调查报告可以发现[5],大幅横摇甚至是倾覆所带来的人员伤亡与财产损失将更为惨重。傅超等[8]结合第2代完整稳性参数横摇前2层衡准和七〇二所开发的稳性评估软件平台,就舭龙骨面积与重心高度对C11集装箱船的参数横摇敏感因素进行分析,并对船艏和船艉的型线进行改进,达到了改善参数横摇的目的。但对此类船型开展3个层次的全面校核工作的并不多。因此,在远洋货轮航行安全性更受关注的当代,对万箱级集装箱船舶进行安全性评估的意义将显得格外突出,也可以更好地指导超大型集装箱船总体设计,为提高安全水平提供更具基础性的研究。
IMO参数横摇第2代完整稳性规则预计将于2019年定稿,其中第1、第2层衡准规则已趋成熟,公式体系也已逐渐被众多研究机构所认可。Umeda等[9]将参数横摇简化为单自由度横摇运动模型,其中非线性回复力采用与波陡相关的非线性函数进行表达。梁海滨等[2]基于参数横摇衡准,采用多元线性回归方法计算了静水中的回复力系数,并运用二分法求解横摇幅值,根据对某渔政船的计算结果,为其航行安全性提供了操作指导。但是对于第3层衡准,不同计算方法与模型的提案较多,且依旧处于样船计算阶段,还未形成较为系统与完整的衡准框架。因此在定稿前,丰富第3层衡准的样船信息与校核资料就变得十分具有研究价值。
针对此,Bulian[10]考虑通过静水力计算得到的垂荡和纵摇运动对参数横摇的影响,提出一种1.5自由度模型,得到了一种较为准确的参数横摇时域模拟方法。Spanos和 Papanikolaou[11]采用基于脉冲响应函数法的六自由度模型对渔船和滚装船进行了数值模拟,结果显示横摇与纵摇耦合,非线性回复力对参数横摇计算结果影响较大。Sadat-Hosseini等[12]采用 CFD 方法研究了一艘水面舰艇的参数横摇问题,发现在迎浪下模拟结果与实验结果吻合较好,但采用CFD计算耗时巨大。
本文拟根据在迎浪中航行的某10 000 TEU集装箱船的装载及稳性计算书,对各个装载工况逐一进行计算。先对第1层衡准进行判定,若不符合要求,则需要进行第2层衡准的1stcheck与2ndcheck判定。鉴于参数横摇的强非线性,其受横摇阻尼、非线性回复力计算等因素的影响较大,又考虑到工程实际问题计算的相对简便与实用性,提出并自主研发了基于典型的弱非线性三自由度(横摇、垂荡和纵摇)模型,以对不满足第2层衡准要求的载况进行迎浪规则波中的参数横摇时域模拟。最后,将对10 000 TEU集装箱船在不同航速、波高和波频时发生参数横摇的情况进行数值模拟,并分析敏感工况的特征,进行航行安全性评估,提出规避措施。
1 IMO参数横摇第1 层薄弱性衡准
第1层衡准基于经验公式[7]。若一艘船满足以下条件,则可判定该船对于参数横摇不敏感:

式中:ΔGM为当波浪通过船体时船舶稳性高的变化幅度;GM为船舶在静水条件下计算所得载况的初稳性高;RPR为标准值,具体计算公式如下:
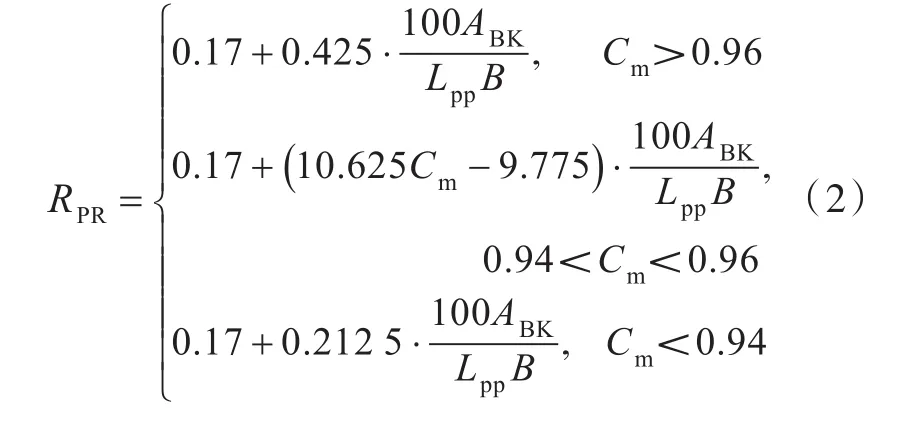
式中:Cm为舯横剖面系数;ABK为不计入附体的舭龙骨侧投影面积之和,m2。
10 000 TEU集装箱船的主尺度如表1所示。

表1 10 000 TEU集装箱船主尺度Table 1 Main dimensions of 10 000 TEU container ship
校核计算结果如图1和图2所示。经对比可知,对于吃水较小(d<10 m)的空船以及各种情形下的压载工况,其重心高度远低于载况,GM值较大(GM>12 m),ΔGM/GM计算值较小,更容易通过衡准。

图1 参数横摇第1层薄弱性衡准结果Fig.1 The first level criterion results of parametric roll

图2 ΔGM/GM随初稳性高GM的变化Fig.2 Variation of ΔGM/GMwithGM
对于吃水d较大的载况,GM的值主要取决于重心G的高度,即甲板上集装箱装载的层高。研究表明,集装箱布置层高越低,整船重心越低,GM越大,ΔGM/GM计算值越小,参数横摇第1层衡准校核通过率越高。在不改变集装箱布置形式的前提下,亦可通过将重型集装箱尽可能往货舱堆积,轻型集装箱往甲板堆放的方式来降低全船重心。
经计算校核,在10 000 TEU集装箱船的89个载况中,有14个载况通过了参数横摇第1层薄弱性衡准,剩余的75个载况未通过,需要进行第2层衡准。
2 IMO参数横摇第2 层薄弱性衡准
根据参数横摇草案[7],用于实船敏感性预报的入射波条件采用国际船级社协会(IACS)推荐的不规则波散布图,所有海况将采用Grim[13]的等效波理论换算为等效规则波。第2层薄弱性衡准相对于第1层衡准更加严密。若一艘船舶满足以下任意一个条件,可以认为其不会发生参数横摇:
1)1stcheck计算所得的C1值小于RPR0;
2)1stcheck计算所得的C1值大于RPR0,且2ndcheck所得的C2值小于RPR1。
2.1 1stcheck算法
1stcheck算法通过对第1层衡准的入射波条件进行拓展,通过对若干等效规则入射波进行加权计算,确定船舶对于参数横摇的敏感性指数。

式中:C1为敏感性指数;RPR0为1stcheck标准值。当满足式(3)的条件时,认为船舶能够满足1stcheck的要求,具体计算过程参见文献[9]。
2.2 2ndcheck算法
2ndcheck采用了基于非线性力学方法的单自由度(1-DOF)横摇运动方程,用于参数横摇幅值的预报,并在此基础上进行敏感性分析。运动方程为

式中:φ为船舶横摇角;GMmean为波浪中稳性高变化的平均值;GMamp为波浪中稳性高变化量的幅值;ωφ为横摇固有圆频率;ωe为遭遇频率;l2k+1为采用最小二乘法拟合静水中的GZ曲线得到的拟合系数,其中k为拟合阶数;α,γ分别为线性和三次横摇阻尼系数,对于缺乏横摇衰减试验结果的情况,可采用简化的Ikeda方法[14]计算。
对于不同的傅汝德数Fr,在顶浪状态下,计算船舶横摇角度超过25°的概率,取概率的平均值即得到敏感性指数C2。若

则判定船舶校核的该载况对于参数横摇现象不敏感。
C2的计算公式为
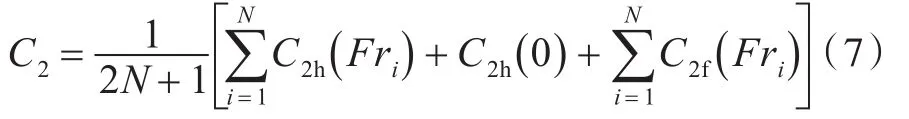
式中,C2h(Fri)和C2f(Fri)分别为以Fri迎浪和随浪航行时C2的分量。其中,Fri的取法如下:

式中:L为船长;g为重力加速度;Vs为服务航速;N为浪向间距数,IMO最新建议取N=3[15]。
2.3 校核结果
经过第1层薄弱性衡准的校核与筛选,将剩余未通过的75个载况进行第2层衡准,分别进行1stcheck与2ndcheck的计算。
1stcheck校核计算结果如图3所示。结果的分布基本上呈现出GM值越大,计算值C1也越大的情况。

图3 参数横摇第2层衡准1stcheck校核计算结果Fig.3 The second level criterion 1stcheck results of parametric roll
2ndcheck校核计算结果如图4所示。结果显示,75个载况的敏感性指数C2均小于RPR1=0.06。

图4 参数横摇第2层衡准2ndcheck校核计算结果Fig.4 The second level criterion 2ndcheck results of parametric roll
对于初稳性高大于4.33 m的10个载况,图3中的计算显示,其虽然未通过1stcheck的衡准要求,但在2ndcheck的校核计算中,它们的敏感性指数C2均为0,因此可以认为它们对参数横摇并不敏感。
另外,由于APL CHINA号(C11集装箱船)在太平洋海域开展商业运营的航行中发生了严重的参数横摇事故[5],因次,C11船成为IMO制定参数横摇衡准失效模式的唯一标准样船。本文选取C11船设计吃水载况(吃水d=11.5 m,初稳性高GM=1.928 m)下计算结果C2(C2=0.067 6)与本船的校核结果进行了横向对比(图4),发现本船各载况下的C2值均小于C11船对应的结果。
对于静水中GZ曲线的拟合(式(5)),其拟合范围为从正浮至30°横倾角的部分,GZ曲线的计算以2°为间距,拟合误差应小于5%或0.005 m中的较大值[15]。但经过计算发现,载况14TAS(14T/TEU Arrival at Scantling Draft)的静水GZ曲线在6°,8°,10°的拟合误差分别为 5.98%,5.51%和5.43%,未达到精度要求,因此该载况未通过参数横摇第2层衡准,需要进行直接计算。同时,因该载况接近满载,GM=1.24 m,C2=0.051 3,较接近衡准值0.06,偏于危险,因此有必要继续对其进行直接计算衡准。
3 参数横摇直接计算相关理论
目前,IMO对于参数横摇直接衡准计算的规则尚未完成制定,仅给出了用于直接计算衡准运动的初步要求指南[16]。
本节将采用基于势流理论方法的弱非线性时域三自由度运动预报模型作为直接计算衡准的校核方法。该方法在三维频域势流方法的基础上应用了脉冲响应函数理论,并采用三维压力积分方法考虑了由船体瞬时湿表面积所引起的Froude-Kriloff力和回复力的非线性效应。运动方程式[17]如下:

式中:M和Ixx,Iyy分别为船舶质量和惯性矩;η3,η4,η5分别为船舶的垂向位移、横摇角和纵摇角;c55为纵摇回复力系数;g为重力加速度;t为时间;τ为时间被积参数;μjk(j,k=1,2,3,分别代表垂向、横向和纵向)为附加质量和附加惯性矩,在平均湿表面下求解三维边值问题得到;为横摇粘性阻尼力矩,采用Ikeda方法[14]进行计算;FIS为Froude-Kriloff力与回复力的合力,基于三维压力积分方法计算,且考虑了由船体瞬时湿表面积所引起的非线性效应;辐射力(积分项)和绕射力FD的计算基于三维频域线性水动力方法,辐射力中Kjk的计算基于脉冲响应函数理论,以考虑时延效应

式中:Bjk(ωe)为频域理论计算的兴波阻尼;bjk为对辐射力应用脉冲响应函数理论引起的阻尼项。
4 计算载况与工况
4.1 计算装载
第2节末已提及,14TAS载况由于其GZ曲线的拟合精度不满足第2层衡准的要求,且其敏感性指数C2的计算值接近衡准值,偏于危险,因此需要进行第3层的直接计算。本载况的相关浮态信息如表2所示。

表2 14TAS装载工况浮态信息Table 2 Floating information about loading condition 14TAS
4.2 计算参数与工况设置
计算参数中,Fr从小到大依次选取值为0.05,0.1和0.218(对应的Vs=23.75 kn)。对于入射的规则波,在选取波长时考虑到了3种形式:
1)波长等于船长(λ=Lpp),波陡的选择参考参数横摇第1和第2层衡准[7],对应每种航速下的1~2号工况。
2)根据参数横摇发生的充分条件(船舶的横摇固有周期约等于2倍的波浪遭遇周期Tφ≈2Ti)与波浪色散关系(,其中ωwave为波频,kwave为波数)换算得到波长,波陡的选择参考参数横摇第1和第2层衡准[7],对应每种航速下的3~6号工况。
3)Grim[13]等效入射波浪表中权重占比(根据北大西洋波浪统计数据显示不同波况出现的概率)最大的规则波(λ=287.931 m,H=4.031 m),对应每种航速下的7号工况。
5 直接计算结果与讨论
5.1 瞬时湿表面积分程序验证
本研究中,参数横摇数值模拟程序采用基于NURBS曲面的瞬时湿表面压力积分法来计算非线性回复力和Froude-Kriloff力。
船舶在波浪中水线面积的变化是参数横摇发生的重要原因,主要由初稳性高GM的变化导致。因此,本文采用程序计算了10 000 TEU集装箱船在14TAS载况时与波浪不同相对位置下的GM值,并与通用软件NAPA的计算结果进行了对比,如图5所示。由图可见,两者的结果相差较小,进一步验证了基于NURBS曲面的瞬时湿表面压力积分程序的准确性与有效性。

图5GM随船体与波浪相对位置的变化情况Fig.5 Variation ofGMwith hull and waves'relative position
5.2 校核结果与分析
采用上述波浪条件与航速设置的组合形式进行典型工况的数值模拟分析,输出三自由度(垂荡、横摇、纵摇)时历曲线,给定初始扰动横摇角为0.2°,模拟时长1 200 s。表3所示为不同工况下参数横摇的计算结果,其中,若干算例的“倾覆”被定义为横摇角在某时刻超过了90°。
对于波长等于船长(λ=Lpp=320 m)的工况Ⅰ-1,Ⅰ-2,Ⅱ-1,Ⅱ-2,Ⅲ-1和Ⅲ-2,波陡的取值合理,仅在Fr=0.05低航速的2个工况(Ⅰ-1,Ⅰ-2)出现了微幅的参数横摇现象。工况Ⅰ-2下的三自由度时域模拟曲线如图6所示。从中可以看出,在400 s时横摇开始显现并逐渐增大,600 s后,趋于稳定幅值(2.98°)下的参数横摇、垂荡与纵摇运动在后期在小范围内稳定振荡。
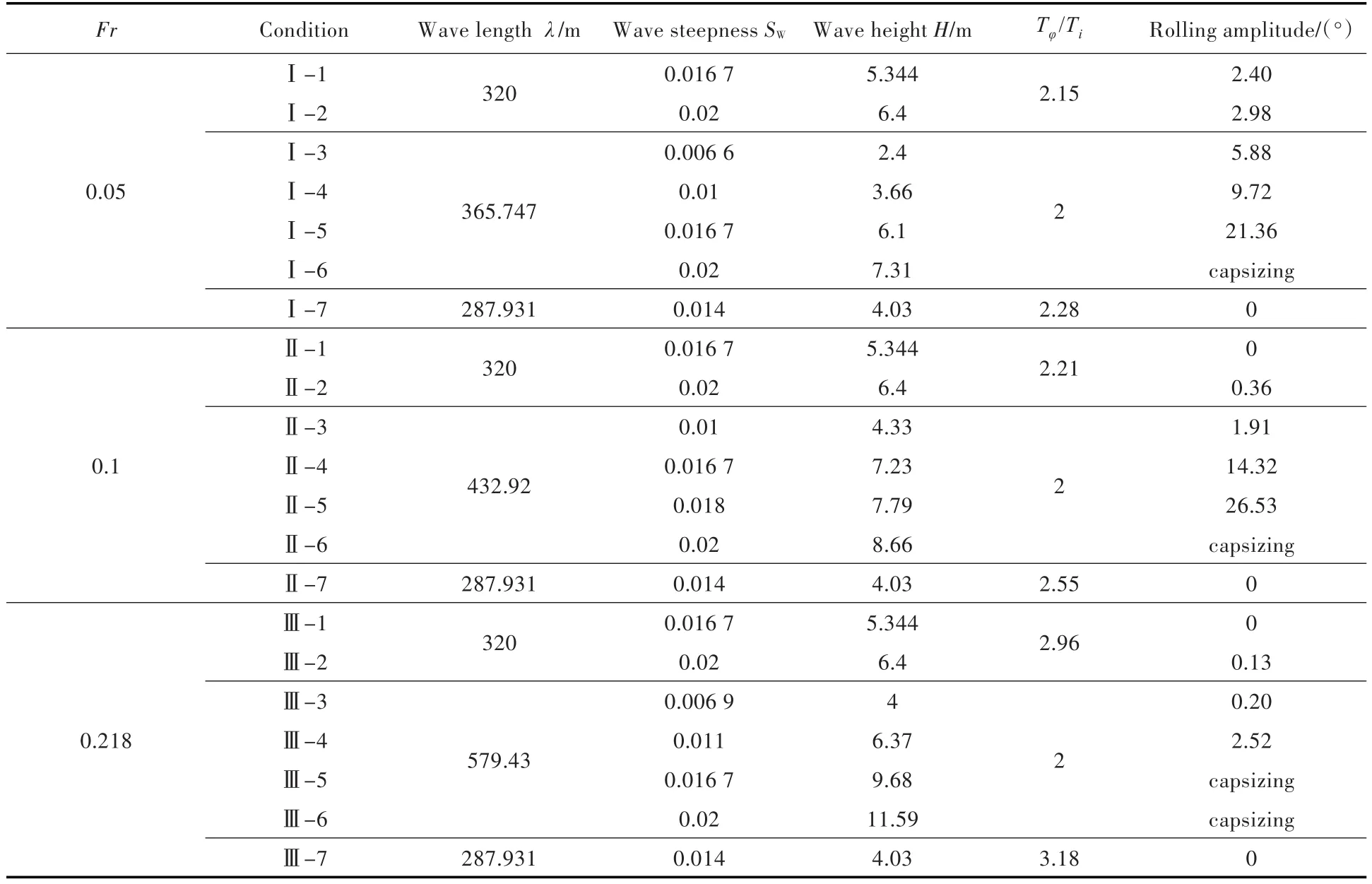
表3 规则波下不同工况参数横摇计算结果表Table 3 Parametric roll results of different conditions in regular waves

图6Ⅰ-2工况下的垂荡、横摇、纵摇时历曲线Fig.6 Time history curves of heaving,rolling and pitching at conditionⅠ-2
当横摇固有周期约等于波浪遭遇周期的2倍时,更易发生参数横摇,在相似波高下,横摇幅值远大于λ=Lpp的波况。图7所示为Ⅱ-6工况下的三自由度时域模拟曲线。由图可见,在时域模拟的前、中期,垂荡与纵摇较为剧烈,横摇微弱;在倍频关系与较大波高的联合激励下,600 s后,垂荡与纵摇开始出现强非线性效应,横摇亦不断增大,直至800 s后出现倾覆。对这2个工况(Ⅰ-2和Ⅱ-6)而言,出现显著参数横摇的时间均较晚。

图7 Ⅱ-6工况下的垂荡、横摇、纵摇时历曲线Fig.7 Time history curves of heaving,rolling and pitching at conditionⅡ-6
5.3 直接计算衡准中危险工况的特征分析
根据表3的计算结果不难发现,当船舶处于迎浪规则波条件下航行,且在规则波波长满足λ=Lpp入射时,10 000 TEU集装箱船从低到高的3个航速对参数横摇均显示出不敏感;而当规则波波长满足其横摇固有周期约等于2倍的波浪遭遇周期时,参数横摇的发生最为明显,事实上这也是参数横摇发生的条件之一。
图8所示为在入射波满足倍频关系的条件下,不同航速时,发生参数横摇的横摇幅值随波陡与波高的变化情况。对参数横摇的直接计算,一般认为在较长时间的时域模拟中,船舶横摇角超过25°即发生了参数横摇[17],因此在图8中给出了各航速下发生参数横摇的临界波陡与临界波高。

图8 不同航速下横摇幅值随波陡与波高的变化(Tφ≈2Ti)Fig.8 Variation of amplitude of rolling with wave steepness and wave height at different speeds(Tφ≈ 2Ti)
由图可以发现,当以临界波陡作为标准分析各工况参数横摇的敏感性时,不同航速下临界波陡值的分布缺少规律;而当以临界波高为标准分析时,临界波高与航速的分布具有较好的相关性,因此,应以波高条件作为超大型集装箱船参数横摇衡准计算时危险工况的选择标准。当船舶处于低航速(Fr=0.05)时,发生参数横摇的临界波高相对较小(H=6.2 m),属于相对危险工况,且相比其他航速,此时对应的入射波波长与Grim[13]的等效入射波浪表中权重占比最大的规则波最为接近,意即更加接近实海域条件。
5.4 实海域航行安全性评估
基于弱非线性时域三自由度运动预报模型,对于10 000 TEU集装箱船而言,低航速对参数横摇现象的发生更加敏感。在实际航行过程中,若遇长波高幅的连续规则涌浪,则需要提高航速,避开倍频区间,以保持在横向干扰小的纵浪下航行,避免大幅横摇。
实际上,对14TAS载况参数横摇的危险性评估相对来说较为保守。首先,计算所得的敏感工况几乎都满足倍频条件;其次,只有当航速较低且大于临界波高时才有机会发生参数横摇。实际航行中若遇此恶劣海况,驾驶员需要更改艏向至迎浪,必要时,需要采取减速停船、集装箱稳固绑扎等相应的措施来避免失稳或倾覆。
危险工况中出现的大幅参数横摇现象几乎都发生在时域模拟的后期,且前、中期已经开始逐渐显现横摇增大的现象。此时,考虑到参数横摇的情形,驾驶员需按航行手册与操作指南及时采取相应的规避措施,以避免横摇的进一步增大。而降低重心高度、适当提高航速、尽量避免波浪倍频关系的满足等均能有效规避参数横摇的发生。
6 结论
鉴于超大型集装箱船对参数横摇安全性评估要求较高,校核意义突出,本文以一艘10 000 TEU集装箱船实船为研究对象,对其各载况进行了IMO第2代完整稳性的参数横摇薄弱性全面校核计算,得到以下主要结论:
1)根据第1层衡准结果,降低船舶重心高度可显著减小波浪中稳性高的变化幅度,对改善参数横摇作用明显。
2)参考第2层衡准的结果,对于初稳性高GM越大的载况,敏感性指数C1也越大;敏感性指数C2较大载况的GM值分布在约1 m外。
3)随着波陡的增加,由于波浪中回复力变化大,参数横摇幅值也变大。对于满足倍频关系的危险波况,需要针对特定的船舶选择不同航速下的临界波高作为校核的计算取值。
4)航速对参数横摇的影响较大,根据直接计算结果,航速增大在一定程度下会对参数横摇存在抑制作用。
5)Grim[13]的等效入射波浪表为基于北大西洋波浪的统计数据,在迎浪状态下,对于其中权重占比最大的规则波,10 000 TEU集装箱船在3个航速下对参数横摇均不敏感。
[1]International Maritime Organization(IMO).Develop⁃ment of second generation intact stability criteria[C]//Sub-committee on stability and load lines and on fish⁃ing vessels safety(SLF)55th session.London:Interna⁃tional Maritime Organization,2013.
[2]梁海滨,马坤.基于参数横摇的航行安全性研究[J].中国造船,2015,56(增刊1):185-192.LIANG H B,MA K.Research of navigation safety based on parametric roll[J].Shipbuilding of China,2015,56(Supp 1):185-192(in Chinese).
[3]DALLINGA R P,BLOCK J J,LUTH H R.Excessive rolling of cruise ships in head and following waves[C]//RINA International Conference on Ship Motions&Ma⁃neuverability.London,UK:[s.n.],1998.
[4]CHU J L,WU C S,LU J,et al.Study on a 3D time-domain method to predict parametric rolling of a ship in regular head seas[J].Journal of Ship Mechan⁃ics,2016(12):1513-1522.
[5]FRANCE W N,LEVADOU M,TREAKLE T W,et al.An investigation of head-sea parametric rolling and its influence on container lashing systems[J].Marine Technology,2003,40(1):1-19.
[6]LEVADOU M,VEER R V.Parametric roll and ship de⁃sign:contemporary ideas on ship stability and capsiz⁃ingin waves[M].Netherlands:Springer,2011:307-330.
[7]International Maritime Organization(IMO).SDC 1/INF.8.Information collected by the correspondence group on intact stability regarding the second genera⁃tion intact stability criteria development[C]//Ship De⁃sign and Construction(SDC)1st Session.London:In⁃ternational Maritime Organization,2013.
[8]傅超,马山,段文洋,等.C11集装箱船参数横摇发生敏感性因素分析和改善措施研究[C]//2014年全国船舶稳性学术研讨会论文集.无锡:中国造船工程学会,2015.
[9]UMEDA N,HASHIMOTO H,VASSALOS D,et al.Nonlinear dynamics on parametric roll resonance with realistic numerical modelling[J].International Ship⁃building Progress,2004,51(2/3):205-220.
[10]BULIAN G.Nonlinear parametric rolling in regular waves—a general procedure for the analytical approxi⁃mation of the GZ curve and its use in time domainsimulations[J].Ocean Engineering,2005,32(3/4):309-330.
[11]SPANOS D,PAPANIKOLAOU A.Numerical simula⁃tion of parametric roll in head seas[J].International Shipbuilding Progress,2007,54(4):249-267.
[12]SADAT-HOSSEINI H,STERN F,OLIVIERI A,et al.Head-wave parametric rolling of a surface combatant[J].Ocean Engineering,2010,37(10):859-878.
[13]GRIM O.Beitragzudem problem der sicherheit des schiffesimseegang[J].Shiff und Hafen,1961,6:490-497(in German).
[14]KAWAHARA Y,MAEKAWA K,IKEDA Y.A simple prediction formula of roll damping of conventional car⁃go ships on the basis of Ikeda's method and its limita⁃tion[C]//Proceedings of the 10th International Confer⁃ence on Stability of Ships and Ocean Vehicles.Neth⁃erlands:Springer,2009:387-398.
[15]International Maritime Organization(IMO).Finaliza⁃tion of second generation intact stability criteria,amendments to Part B of the 2008 IS code on towing,lifting and anchor handling operations[C]//Ship De⁃sign and Construction(SDC)3rd session.London:In⁃ternational Maritime Organization,2016.
[16]International Maritime Organization(IMO).Informa⁃tion collected by the correspondence group on intact stability regarding the second generation intact stabili⁃ty criteria development[C]//Ship Design and Con⁃struction(SDC)1st session.London:Internation Mar⁃itime Organization,2014.
[17]周耀华,马宁,顾解忡.集装箱船横摇惯性矩计算方法对参数横摇敏感性预报影响研究[J].中国造船,2013,54(3):11-20.ZHOU Y H,MA N,GU X C.Effect of calculation methods of roll moment of inertia on sensitivity predic⁃tion of parametric rolling for container ships[J].Ship⁃building of China,2013,54(3):11-20(in Chinese).
Comprehensive calculation and safety assessment of parametric roll of very large container ship
MA Chengyuan1,2,MA Ning2,3,WANG Tinghao1,2,GU Xiechong2,3
1 School of Naval Architecture,Ocean&Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China
2 Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration,Shanghai 200240,China
3 State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China
As the significant variation of GM in waves for very large container ships,strict demands are raised for this ship type in the evaluation and safety assessment of parametric roll.Targeting a 10 000 TEU container ship sailing in head sea,this study conducts a series of calculations and evaluations on parametric roll motion in which each loading condition is calculated step-by-step.Direct calculation is conducted if neither Level 1 nor Level 2 is satisfied.In this paper,an independently developed time-domain simulation is conducted for loading conditions that fail to match the Level 2 criteria,which is based on a typical 3-DOF weakly nonlinear numerical model.Ship velocity and wave conditions are taken into consideration to explore sensible conditions concerning parametric roll.Finally,according to the results,corresponding safety assessments and several avoidance measures are proposed,such as reducing the height of the center of gravity and raising the speed moderately.In addition,if wave predictions can be detected in advance,the circumstance of the natural rolling period being twice as great as the encountering period should be avoided,which isthe most sensible factor for inducing parametric roll.Comprehensive calculation and checking for the 10 000 TEU ship can instruct the general design and improve safety for very large container ships;as a result,remarkable engineering applications and reference value can be recognized.
very large container ship;parametric roll;direct calculation;safety assessment
U661.32
:ADOI:10.3969/j.issn.1673-3185.2017.03.002

http://kns.cnki.net/kcms/detail/42.1755.TJ.20170512.1301.038.html期刊网址:www.ship-research.com
马骋远,马宁,王廷昊,等.超大型集装箱船参数横摇全面校核与安全评估[J].中国舰船研究,2017,12(3):7-15.
MA C Y,MA N,WANG T H,et al.Comprehensive calculation and safety assessment of parametric roll of very large container ship[J].Chinese Journal of Ship Research,2017,12(3):7-15.
2016-11-28< class="emphasis_bold">网络出版时间
时间:2017-5-12 13:01
财政部、教育部重大科研专项基金资助项目(GKZY010004);国家自然科学基金资助项目(51579144)
马骋远,男,1992年生,硕士生。研究方向:波浪中的船舶稳性与安全性设计。E-mail:sjtumcy@163.com
马宁(通信作者),男,1961年生,博士,教授,博士生导师。研究方向:船舶与海洋结构物耐波性及安全性,海洋波浪数值模拟预报。E-mail:ningma@sjtu.edu.cn

