规则波浪中舰船纯稳性丧失计算研究
朱军,刘瑞杰,葛义军,王智宇,黄昆仑
1海军工程大学舰船工程系,湖北武汉430033
2海军装备研究院,北京100073
规则波浪中舰船纯稳性丧失计算研究
朱军1,刘瑞杰2,葛义军1,王智宇1,黄昆仑1
1海军工程大学舰船工程系,湖北武汉430033
2海军装备研究院,北京100073
[目的]波浪中纯稳性丧失是第二代舰船完整稳性中稳性薄弱性的衡准之一。针对波浪中大倾斜角稳性计算发散问题,[方法]以静水面坐标系为基准,定义了广义纵倾角和广义吃水变量,推导出物理含义清晰的波面方程。在Froude-Krylov假定条件下,结合AutoCAD二维图形面域计算技术和VBA编程方法,提出了规则波浪中舰船纯稳性丧失的计算方法。针对一艘具有阶梯式甲板的舰船,计算了规则波浪中舰船复原力臂曲线,证明大横倾状态具有一致收敛性。[结果]计算得到了规则波浪中稳性变化规律:纵向波浪中,波面高于甲板或低于船底导致有效水线面消失是稳性降低的主要原因;斜浪和正横浪中,波面相对船体横剖面倾斜引起的不对称性,是稳性大幅度降低的主要原因。[结论]计算收敛一致性表明,基于广义纵倾角定义的计算方法可成为评估舰船波浪中纯稳性丧失的有效手段。
舰船;纯稳性丧失;规则波浪
0 引 言
20世纪30年代,Kempf[1]通过不断调查和分析发现,当船舯位于波峰附近时,船舶稳性相比静水会有所下降,反之,当船舯位于波谷附近时,稳性有所上升。1961年,Paulling等[2-3]研究了波浪中船舶的稳性,其后通过在旧金山湾中进行随浪、尾斜浪和横浪环境中的大尺度比船舶试验,并结合时域模拟分析方法,发现了船舶在波浪环境中的倾覆机理。Grim[4]提出了有效波的观点,将海洋中的随机波转化为规则波。上世纪80年代,Hamamoto等[5-6]对尾斜浪的船舶稳性计算方法进行了研究,但是大横倾角计算时出现发散情况,随后他建立了一个新的坐标转换体系研究船舶在波浪中的操纵性[7]。Fang等[8]在 Froud-Krylov假定的基础上考虑散射和绕射的影响,计算了船舶在斜浪中的复原力臂。Kreuzer等[9]在考虑船舶横摇、纵摇及垂荡的基础上对船舶倾覆问题进行了研究。
国内孔祥金等[10]为了解决大横倾角下计算的发散问题,采用摄动法计算波面下船体横剖面积和中心;谢微[11]对稳性薄弱性的纯稳性丧失进行了研究;周耀华等[12-13]对纯稳性丧失薄弱性的一、二层衡准进行了计算分析;胡丽芬等[14]综述了参数激振横摇的研究现状。朱军等[15]应用AutoCAD的图形面域技术数值计算了舰船在静水中的稳性与破损稳性。
研究发现,波浪中大横倾角的稳性计算出现发散的原因,在于绕船体坐标轴定义的纵倾角与纵向倾斜力矩(重力与浮力构成的力矩)方向不一致,横倾角越大偏差也越大。在横倾角为90°的极端情况下,纵倾角在水平面内转动,而纵向倾斜力矩则始终是垂直水平面的。这导致大横倾角下纵倾力矩平衡方程式的不匹配。
本文将定义绕静水面轴线转动的广义纵倾角,以及垂直静水面的广义吃水,保证纵向倾斜力矩平衡方程式的匹配性。
1 船体坐标系下的波面方程
1.1 坐标系定义
静水面固定坐标系O-xyz如图1所示,平面Oxy与静水面重合,Oz坐标轴垂直向上,波面方程为

式中:λ为波长;Hw为波高;χ为浪向角;ξ0为波峰位置。当ξ0=0时,波峰线通过坐标原点,当ξ0=λ/2时,波谷线通过坐标原点。

图1 静水面固定坐标系Fig.1 Fixed coordinate system of static surface
船体固定坐标系B-xByBzB如图2所示,以左右对称面、龙骨基面和船舯面的3面交点B为坐标系原点,BxB轴指向船艏,ByB轴指向右舷,BzB轴垂直向上。T为静水船舯处的吃水,得到静水面固定坐标系与船体坐标系的转换关系为


图2 船体坐标系Fig.2 Coordinate system on hull
令静水面坐标系绕O点转动ϕ角度(图3(a)),再令静水面坐标系绕沿静水面平移ΔT(图3(b),相当于船体下沉),最后令静水面坐标系绕Oy轴旋转θ角(相当于船体绕静水线面轴线转动),则转动后两坐标系的转换关系为
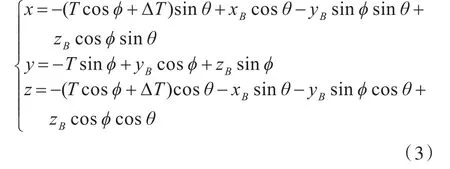


图3 坐标系旋转与平移Fig.3 Coordinate systems transformed by rotation and shift
1.2 船体坐标系下波面方程
令式(3)的第3项z=0,则到船体坐标下静水面方程为

将式(1)代入到式(3)的第3项中,得到船体坐标下的波面方程为

式中,x和y由式(3)的第1项和第2项确定,这是一个隐式方程。
式(5)为波面在船体坐标系下的表达式,当吃水T、吃水增量ΔT、横倾角ϕ和纵倾角θ一定时,波面方程唯一确定。值得注意的是,T和ϕ与通常的定义是一致的,但吃水增量ΔT是垂直静水面的变化量,即广义吃水,θ则是绕船舯剖面与静水面交线的转动角度,即广义纵倾角。
2 复原力臂计算公式
2.1 舰船平衡条件
平衡条件为舰船重量等于瞬时波面下的浮力,且作用在同一条铅垂线上(垂直静水线面),平衡方程为

式中:ρ为水的密度;g为重力加速度;为瞬时波面下船体的排水体积;(xBb,yBb,zBb)为船体排水体积中心;W和(xBg,yBg,zBg)为船体的重力和重心。排水体积和浮心坐标按二维切片法计算:

式中:A(xB)为瞬时波线下船体横剖面面积;yBc,zBc为对应的面积中心。
2.2 瞬时波面下船体复原力臂
当船体横倾角为ϕ时,在满足式(7)中的第1式(重力与浮力平衡)和第3式(纵倾力矩平衡)条件下,瞬时波面下船体复原力臂GZ为

上述平衡条件和复原力臂计算式是基于瞬时波面下静水压力(Froude-Krylov)的假定,忽略了史密斯的动压修正项(e-kz)。为了简化计算,取波面以下的排水重量作为瞬时浮力,将流体压力近似成p=ρg[z+ςzcos(kx)]。该近似相当于在波峰区域高估了压力,在波谷区域低估了压力,即有效波陡应该比几何波陡略小,通常的近似方法是修正几何波陡,即动压部分取为ςze-kd/2cos(kx),其中d为吃水。因此,修正将不会影响运动的变化规律。
3 数值计算及分析
3.1 图形面域计算技术
本文应用AutoCAD二维图形面域的计算方法[15],通过编程语言VBA二次开发了波浪中舰船稳性计算程序。计算步骤如下:
1)绘制船体横剖面图,形成船体剖面图形面域;
2)按式(5)在对应的剖面处绘制波线,形成包含船体剖面的波线图形面域;
3)提取船体面域和波线图形面域并集的面域特征值(面积和形心坐标);
4)按式(7)积分得到排水体积和体积中心坐标,在满足式(6)第1式和第3式的条件下,由式(8)计算复原力臂。
3.2 波浪中稳性数值计算
本文计算舰船的水线长为125 m,艏楼计入稳性部分,艉部有阶梯型甲板。波浪中稳性计算范围为:浪向角χ分别为 0°,30°,60°和90°;波长船长比λ/L分别为 0.5,1.0和 1.5;波陡Hw/λ为0.01~0.1,波峰相位(2π/λ×ξ0)为0~2π。
3.3 舰船波浪中稳性分析
1)纵向波浪中纯稳性丧失计算分析。
图4为纵向波浪中(浪向角χ=0°)复原力臂计算曲线图。波峰相位(2π/λ×ξ0)=0表示波峰位于船舯,(2π/λ×ξ0)=π表示波谷位于船舯。计算结果表明,波高显著导致稳性丧失,复原力臂的最大值和稳性范围均显著减少;另一个特征是中垂状态(波谷位于船舯)也有显著的稳性丧失。

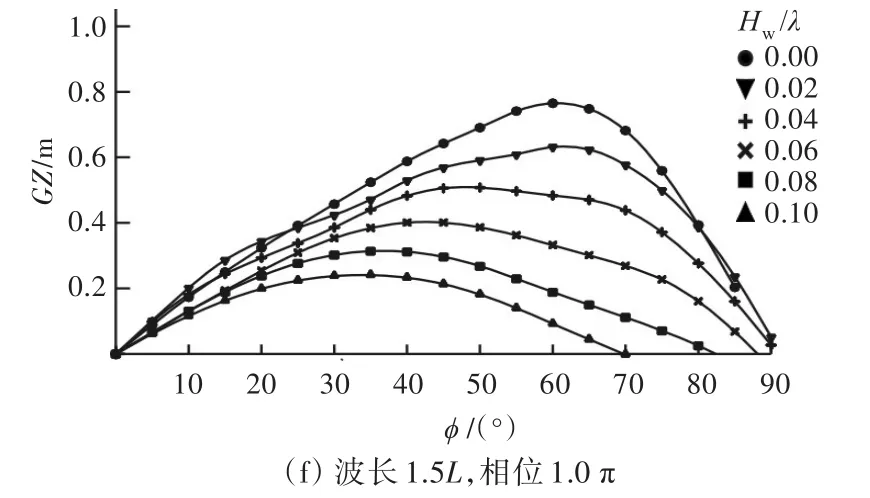
图4 纵向波浪中复原力臂计算曲线(χ=0°)Fig.4 Calculating curves of righting arm in longitudinal waves(χ=0°)
当λ/L=1.0和Hw/λ=0.06时,船体与波面相交位置如图5所示。说明波峰位于船舯时,有效水线面(提供稳性)位于船体中部,船艏和船艉的底部高出波面导致有效水线面丧失;波谷位于船舯时,只有船舯后和船舯前2部分区域为有效水线面,船舯部因波谷低于船体而丧失了有效水线面,船艏和船艉上甲板因波浪淹没也导致有效水线面的丧失。

图5 船体与波面相交位置图(λ/L=1.0,Hw/λ=0.06)Fig.5 The interface between hull and waves on crest and trough(λ/L=1.0,Hw/λ=0.06)
2)正横波浪中纯稳性丧失计算分析。
图6为正横波浪中(浪向角χ=90°)复原力臂计算曲线图,图6给出了波峰相位分别为0.5π和0.75π下2种稳性丧失较为严重的情况。计算结果表明,波高也是导致稳性丧失的主要影响因素,稳性丧失表现在最大复原力臂值随波高增加而大为减少,其次是稳性范围也大为减少。由于波面相对船体横剖面成倾斜状,类似于船体存在初始横倾角,复原力臂曲线呈现左右不对称性,导致最大复原力臂值和稳性范围减少。
3)斜浪中纯稳性丧失计算分析。
图7为斜浪中(浪向角χ=30°)复原力臂计算曲线图。计算结果表明,斜浪状态的稳性特征介于纵向波浪和正横浪之间。波长较短时复原力臂左右不对称性不明显,这是由于波长较短时,波面相对船体横剖面的倾斜方向相反,抵消了倾斜的不对称性。随着波长的增加,倾斜的不对称性变得显著,最大复原力臂值随波高增加明显降低。
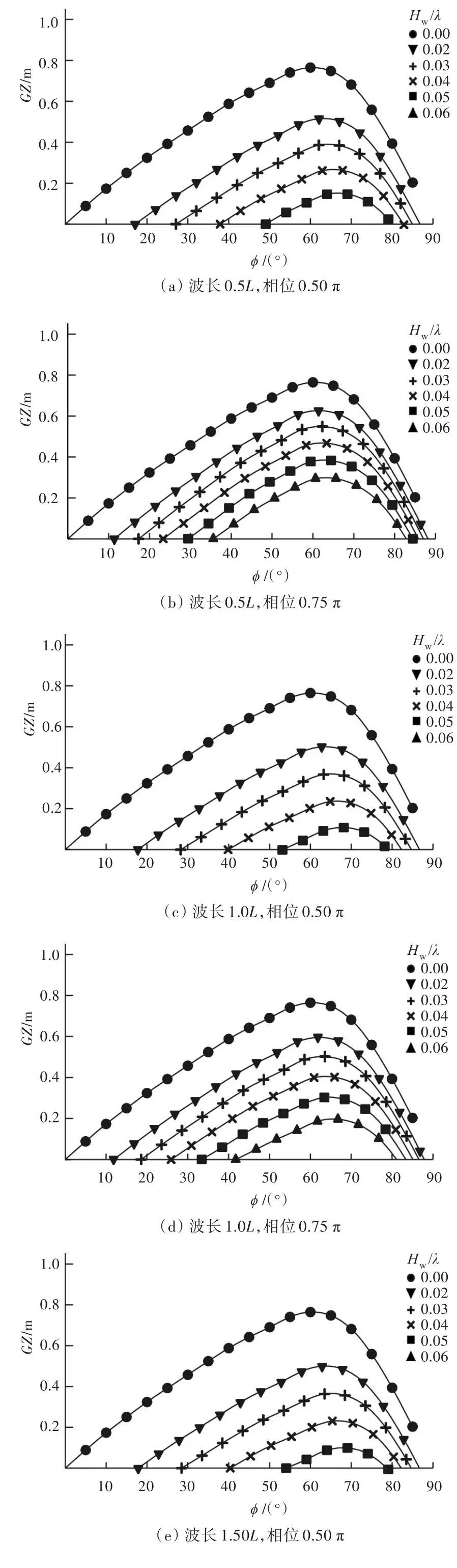

图6 正横波浪中复原力臂计算曲线(χ=90°)Fig.6 Calculating curves of righting arm in beam seas(χ=90°)


图7 斜浪中复原力臂计算曲线(χ=30°)Fig.7 Calculating curves of righting arm in oblique waves(χ=30°)
4 结 论
本文定义了广义纵倾角θ和广义吃水ΔT,推导出了船体坐标系下的波面方程。导出的船体坐标系下的波面方程由5项构成,各物理含义明确,且吃水增量ΔT、横倾角ϕ和纵倾角θ分别主要影响到浮力、横向力矩和纵向力矩,从而使得迭代计算具有稳定收敛特性。在Froude-Krylov假定条件下,对阶梯式甲板舰船波浪中复原力臂计算结果的对比和分析表明:
1)λ/L=1.0是舰船波浪中纯稳性丧失的主要波浪环境,波高是导致稳性丧失的主要因素。
2)纵向波浪中,波谷位于船舯时(某些波高较大时)稳性也会大幅度降低,波面高于甲板或低于船底导致有效水线面消失是其主要原因。
3)正横浪和斜浪情况下,因波面相对船体横剖面的倾斜形成的不对称性是稳性大幅度丧失的主要原因,正横浪情况最为严重。
本文提出的规则波浪中舰船纯稳性丧失直接计算的方法具有稳定收敛特性,且可扩展至船舶摇荡耦合运动计算方法中。
[1]KEMPF G.Die stabilitätsbeanspruchung der schiffe durch wellen und schwingungen[J].Werft Reederei Hafen,1938,19:200-202.
[2]PAULLING J R.The transverse stability of a ship in a longitudinal seaway[J].Journal of Ship Research,1961,4(4):37-49.
[3]PAULLING J R,KAESTNER S,SCHAFFRAN S.Ex⁃perimental studies of capsizing of intact ships in heavy seas[R].U.S.Coast Guard Technical Report,1972.
[4]GRIM O.Beitrag zu dem problem der Sicherheit des Schiffes im seegang[J].Schiff und Hafen,1961,6:490-497.
[5]HAMAMOTO M,UMEDA N,SHIGEHIRO R,et al.Transverse stability of a ship in following sea[J].The Japan Society of Naval Architects and Ocean Engi⁃neers,1982,185:49-56.
[6]浜本剛実,金潤洙,松田秋彦,等.斜め追波中の船の転覆とその原因の分析[J].日本造船学会論文集,1992,172:135-145.HAMAMOTO M,KIM Y S,MATSUDA A,et al.An analysis of a ship capsizing in quartering seas[J].The Society of Naval Architects of Japan,1992,172:135-145(in Japanese).
[7]浜本剛実,金潤洙.波浪中の操縦運動を記述する新しい座標系とその運動方程式[J].日本造船学会論文集,1993,173:209-220.HAMAMOTO M,KIM Y S.A new coordinate system and the equations describing manoeuvring motion of a ship in waves[J].The Society of Naval Architects of Ja⁃pan,1993,173:209-220(in Japanese).
[8]FANG M C,LEE C K.On the dynamic stability of a ship advancing in longitudinal waves[J].International Shipbuilding Progress,1993,40(422):177-197.
[9]KREUZER E,WENDT M.Ship capsizing analysis us⁃ing advanced hydrodynamic modelling[J].Philosophi⁃cal Transactions of the Royal Society A:Mathemati⁃cal,Physical and Engineering Sciences,2000,358(1771):1835-1851.
[10]孔祥金,曹振海.尾斜浪中船舶复原力计算[J].中国造船,1994(2):32-41.KONG X J,CAO Z H.Calculation of righting arm for ships in quartering seas[J].Shipbuilding of China,1994(2):32-41(in Chinese).
[11]谢微.船舶纯稳性丧失薄弱性衡准研究[D].大连:大连理工大学,2014.XIE W.Research on the draft vulnerability criteria of the pure loss of stability of ship[D].Dalian:Dalian University of Technology,2014(in Chinese).
[12]周耀华,张高峰,牛业兴,等.纯稳性丧失衡准实船分析研究[J].中国造船,2015,56(增刊 1):37-47.ZHOU Y H,ZHANG G F,NIU Y X,et al.Study on full-scale ships based on pure loss of stability criteria[J].Shipbuilding of China,2015,56(Supp 1):37-47(in Chinese).
[13]马坤,甘鄂,谢微.船舶纯稳性丧失薄弱性衡准样船计算分析[J].中国造船,2015,56(增刊 1):193-200.MA K,GAN E,XIE W.Sample calculations and analysis on vulnerability criteria of pure loss of stabili⁃ty[J].Shipbuilding of China,2015,56(Supp 1):193-200(in Chinese).
[14]胡丽芬,鲁江,顾民.船舶波浪稳性研究现状分析[J].中国造船,2015,56(增刊1):211-216.HU L F,LU J,GU M.Status analysis of research on ship's stability in waves[J].Shipbuilding of China,2015,56(Supp 1):211-216(in Chinese).
[15]朱军,黄昆仑.舰船稳性与破损稳性的二维图形面域计算法[C]//第九届全国海事技术研讨会论文集.上海:上海市海事交流协会,2003:99-104.ZHU J,HUANG K L.The calculating method of tow-dimension region for ship stability and dam⁃aged-stability[C]//Proceedings of the Ninth National Conference on Maritime Technology.Shanghai:ShanghaiMaritimeExchangeAssociation, 2003:99-104(in Chinese).
Pure loss of stability calculation of naval ship in regular waves
ZHU Jun1,LIU Ruijie2,GE Yijun1,WANG Zhiyu1,HUANG Kunlun1
1 Department of Naval Architecture Engineering,Naval University of Engineering,Wuhan 430033,China
2 Naval Academy of Armament,Beijing 100073,China
The pure loss of stability of a ship is one of the failure modes of the second-generation intact stability criteria.Based on the static surface coordinate system,the generalized pitch angle and draught variable are defined,and a wave equation with clear physical meaning is deduced.Based on the Froude-Krylov hypothesis,combined with AutoCAD 2D surface area computing technology and the VBA programming method,a calculation method of the loss of pure stability of ships in regular waves is proposed.For a naval ship,the righting arm is calculated in regular waves,and the large heel ship state is shown to have an identical convergence.The results of the calculations show that a significant reduction in the meta centric height of the maximum righting arm occurs not just in a wave crest but also in a trough.By analyzing the wave profile under the hull,it can clearly be seen that wave amplitude above the deck or below the bottom of the hull causes the pure loss of stability,and in oblique waves or beam seas,the pure loss of stability is caused the asymmetry of the wave profile on the hull.The coinciding convergence of the calculations shows that the process of the definition of generalized pitch can be employed to assess the pure loss of stability of naval ships in regular waves.
naval ship;pure loss of stability;regular waves
U661.2+2
:ADOI:10.3969/j.issn.1673-3185.2017.03.001

http://kns.cnki.net/kcms/detail/42.1755.TJ.20170512.1303.040.html期刊网址:www.ship-research.com
朱军,刘瑞杰 ,葛义军,等.规则波浪中舰船纯稳性丧失计算研究[J].中国舰船研究,2017,12(3):1-6,15.
ZHU J,LIU R J,GE Y J,et al.Pure loss of stability calculation of naval ship in regular waves[J].Chinese Journal of Ship Research,2017,12(3):1-6,15.
2017-02-16< class="emphasis_bold">网络出版时间
时间:2017-5-12 13:03
朱军,男,1959年生,博士,教授。研究方向:船舶操纵性。E-mail:zhjun101@sina.com
刘瑞杰(通信作者),男,1987年生,博士,工程师。研究方向:船舶水动力。E-mail:jackrygy@126.com

