基于NURBS的球艏构型参数优化与分析

张文山，卢晓平，王中

海军工程大学舰船工程系，湖北武汉430033

基于NURBS的球艏构型参数优化与分析

张文山，卢晓平，王中

海军工程大学舰船工程系，湖北武汉430033

［目的］设计优良的球艏构型能够改变船舶在水中航行时的船艏兴波，对阻力产生影响来改善整个船体的阻力性能，为此需对球艏构型参数进行优化。［方法］基于球艏参数化表达和NURBS理论，对母型球艏构型进行数据点网格生成和定义点反算，根据参数优化需要，利用优化算法对定义点进行优化调整后，给出优化船型球艏，并利用CFD软件进行仿真计算，与母型构型进行阻力和波形对比，将以球艏重心为代表的球艏参数阻力特征直接体现到构型优化结果中。［结果］结果表明，借助于NURBS曲线可有效将球艏参数优化特征体现出来，方法形象直观，可显著提高球艏构型表示和优化的效率。［结论］该方法简化了整个优化过程，并取得预期的减阻效果。

NURBS；兴波阻力；球艏构型参数；优化；CFD

0 引 言

一般来说，安装有减阻型球艏的船型具有较好的水动力性能。船舶兴波阻力有时对船体型线的微小改变反应敏感，而设计优良的球艏构型恰恰能够改变船舶在水中航行时的船艏兴波，从而改善整个船体的阻力性能。船舶水动力性能研究一般包括对水动力性能指标的预报和优化。通过较为便捷的船型建模方法可以简化球艏优化和设计流程。结合参数化CAD设计和利用CFD软件进行性能研究的分析方法与思路在实际应用中具有显著的优势，被广泛应用于球艏和船体优化研究［1］。

早期的研究多是通过比较不同构型参数对球艏阻力性能的影响来得出球艏参数优化的依据，但是缺乏自动生成目标模型的能力［2］。文献［3］基于非线性理论，以阻力性能分析结果对球艏构型进行参数优化，研究方法虽然具有综合性，但没有结合曲线曲面表达工具，优化模型的生成具有短板。文献［4-5］根据参数分析结果对船体整体和局部进行了优化，研究方法和思路具有很好的借鉴意义，但在球艏建模过程中缺少对样条曲线形状的精确控制，导致得到的优化数值结果离散化。文献［6］通过阻力比较和波形分析对球艏的减阻效果进行了验证，具有很好的借鉴意义。

本文将采用具有较强图形处理和三维显示功能的建模软件Rhinoceros，利用其面元生成方法进行球艏型值数据点的可视化表达，并与等参化的NURBS曲面节点相互转换。整个参数优化的过程包括4个环节：

1）对母型球艏构型进行数值读入和数据点网格生成，并对球艏构型进行参数化表达，形成沿球艏3个方向的截面曲线。

2）根据这些截面数据点，反算NURBS曲线定义点。

3）根据已有的研究结果，对截面曲线定义点进行目标性优化，主要是通过改变横截面的重心高度来实现，再重新导入建模软件中生成优化构型。

4）将生成的优化构型运用CFD软件进行计算，并与母型球艏船型的阻力和兴波进行对比。

1 球艏参数化描述

非均匀有理B样条（Non-Uniform Rational B-Spline，NURBS）方法侧重于使用统一的数学模型来表达船体局部或整体的型线特征，并能减小不规则模型建模放样和导入CFD软件过程中所造成的不准确和不便捷［1］。本文简化了曲线表达的难度，只做简单探索，故而将权因子设置为常数，取用简化的NURBS曲线曲面来处理所遇到的问题。NURBS在船舶设计中的应用不仅能够减小面元逼近船体局部曲面时的计算误差，而且其将仿真计算和模型建立在球艏优化和设计的研究过程中有机结合起来，提高了方案优化和阻力预报的效率。

在球艏优化和设计过程中，一般的步骤是先将船体型值参数作为表征船体形状的主要依据，借助CAD软件调用功能来实现模型建立，再利用CFD软件进行仿真运算来预报和验证船体的水动力性能参数。而在明确了球艏参数［7］对船体阻力影响规律的情况下，进行球艏参数化描述，是通过控制参数变化来实现构型优化和表达的基础。

参数化是截面曲线表达的数值简化形式。设计优良的截面曲线能够较好地表达和控制球艏体积在纵向、横向和垂向3个方向上的几何分布，而这些体积分布特征恰恰会影响到球艏波的波幅值［6］，其具体的影响能在阻力和波形分析中体现出来［4］。为便于球艏形状的表达，描述球艏形状的参数需要少而精、简洁明快又能精准表达结构特征。Kracht［7］对描述球艏形状的定量性参数予以了总结，其中包括3个线尺度参数和3个体/面尺度参数：

1）球艏宽度系数CBB：球艏部分最大宽度BB与船宽BMS的比值；

2）长度参数CLPR：球艏最大长度LPR与船体水线面长度LWL的比值；

3）深度参数CZB：球艏横截面重心高度ZB与船体在艏垂线处吃水TFP的比值；

4）横剖面截面参数CABT：球艏横截面积ABT与船舯截面积AMS之间的比值；

5）纵剖面参数CABL：球艏在中纵剖截面上的面积ABL与船体中纵剖截面面积AMS之间的比值；

6）体积参数C∀PR：球艏体积∀PR与船体排水体积∀WL之间的比值。

简言之，球艏的截面形状和体积参数影响着球艏的整个形状和体积分布。其中，体积参数在球艏纵向、横向和垂向3个方向截面形状的投影，表征为球艏在3个方向的几何分布。

举例来说，横剖面的重心高度（均匀分布球体截面面积分布的垂向高度）决定了横剖面形状，当重心高度更接近水面时，横剖面形状趋向于呈倒三角型，反之则呈正三角型，重心数值介于二者则呈“○”型。根据参数化表示的原则，可以利用球艏垂向重心的高度来进行描述，亦可看做是球艏在垂向的体积分布［4］，还可以根据定义点的分布特征来确定。而这又可以通过控制角来区分，其中倒三角型截面具有比其他两者更大的船底斜角。因而在下文进行实例演示时，将采取球艏重心垂向平移的方式来展示型线优化与参数优化之间的关联。

2 球艏曲面表达与样条曲线生成

2.1 三阶NURBS基本理论与运算

NURBS基函数是按照de Boor-Cox递推公式给出，为方便应用，现采用次数直接给出［8］。

设U={u0，...，um} 为递推函数的实数序列，即ui≤ui+1(i=0，...，m-1)，ui称为节点，U为节点矢量，则第i个n次NURBS基函数定义为：

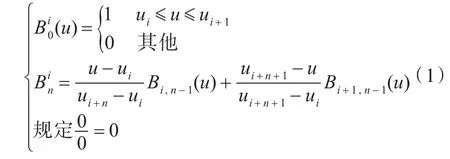
故而可得n次NURBS曲线可表示为如下形式：

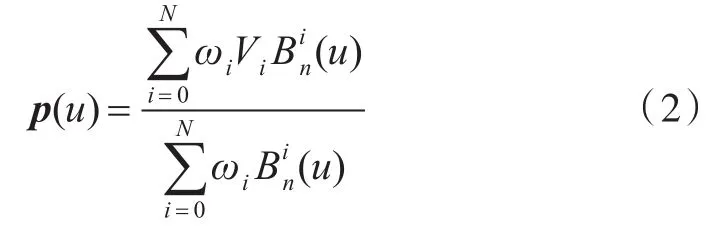
式中：Vi(0≤i≤N)为定义点，定义点顺序连接即构成控制多边形，又称特征多边形；ωi(0≤i≤N)为定义点Vi(0≤i≤N)的权因子，为简化文中的计算，所有的权因子均取值为1(即ωi=1;i=0，...，N)；为由节点矢量U={u0，...，un+N+1} 决定的n次规范NURBS基函数，且满足

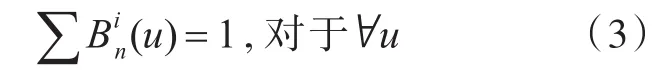
由式（2）和式（3），可得

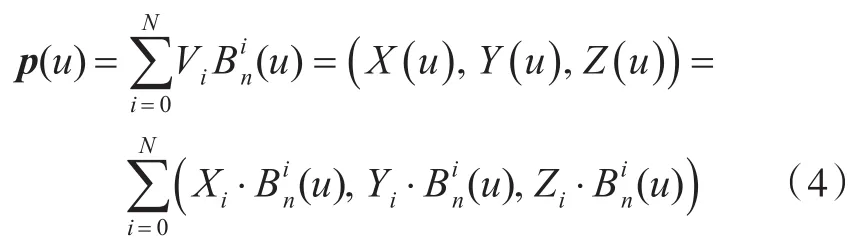
这里，Vi=(Xi，Yi，Zi)(i=0，...，N)，为 NURBS定义点的坐标。假设给定船舶型值参数，利用三次NURBS曲线理论，若原曲线设置有4个数据点，便可相应求得定义点Vi(N=3)。进行定义点反算，即可求解点集(X(u)，Y(u))，其表达式为

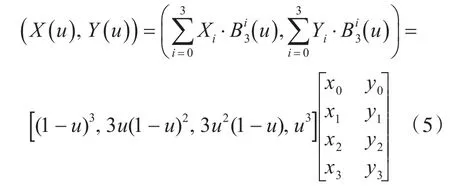
易得第1定义点V0(x0，y0)和第4定义点V3(x1，y1)与样条曲线的首末数据点重合。对于三次NURBS开曲线，方程组的数目不足以决定未知定义点，通常需要增加额外的边界条件来构成附加方程，以满足线性方程组个数与未知数相同。本文选用常用的切矢边界条件，取曲线区段两端节点重复度r=4，故而三次NURBS曲线的首末定义点即为首末数据点，即

且在首末端点处分别有切矢和，令为u的一阶向前差分，则得附加方程：

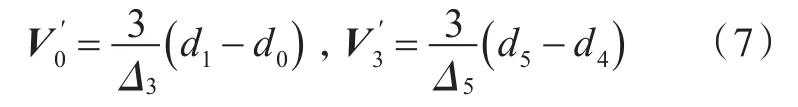
在实际计算中，定义点反算需考虑实际生成的曲线和几何体形状的，同时，还需要考虑实际插值计算的误差，以避免计算的不稳定。

然而实际的数学运算必然会存在一定的数值误差，如果运算误差在允许的范围内，则可忽略不计；若计算误差过大，则需要根据偏差趋向（在模型放样过程中体现为曲线曲面的不光顺或者变形）来调整约束条件和算法的合理性［9］。

2.2 球艏曲面数据点网格化和定义点计算实例

NURBS曲面亦可写成2个参数方向上的形式，即

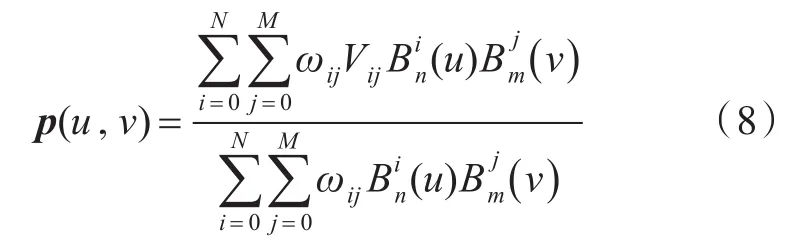
在曲面定义点反算问题中，由于可能出现相邻位置曲线上数据点对应的节点矢量不能保证相等，所以需要将曲线参数予以规范。实际计算过程中，曲面和曲线定义点反算问题的基本步骤相同，其中用于求解定义点线性方程组系数矩阵的阶数较高，计算略繁琐。本文中涉及到的构型为球艏局部，故不会出现类似的问题［5］。

图1所示为球艏三维轮廓线示意图。球艏的站位划分在曲率变化较大的位置要求适当加密，以满足型值点插值计算的精度，同时还需避免最终的定义点计算过于复杂。

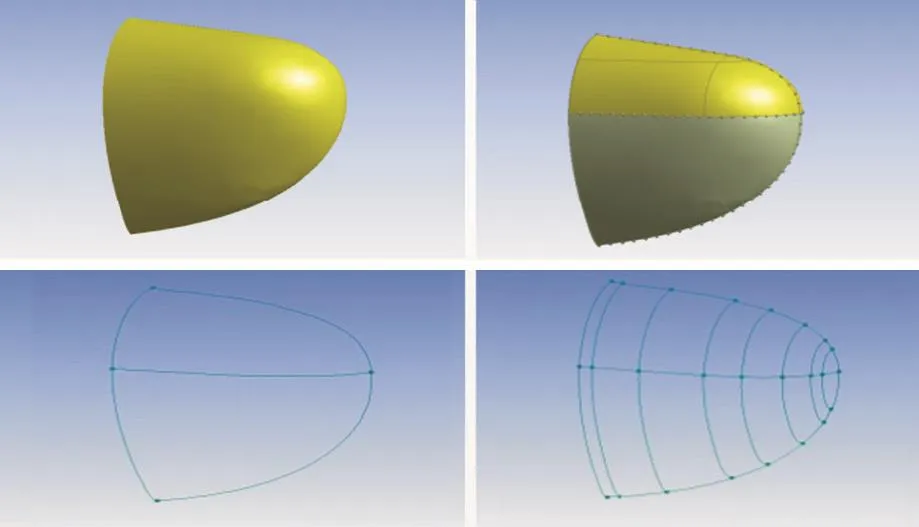
图1 球艏轮廓线Fig.1 Outline curves of bulbous bow

如图2和图3所示，通过已有的艏部型线，明确球艏在垂向、纵向和横向等3个不同方向的型线曲线分段、数据点的数目及端点处的切矢，利用这些数据，可按照之前的方法对定义点进行反算。图中Pi（i=1，2，3，…）为数据点。

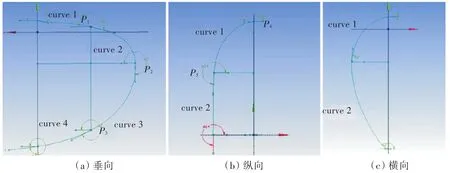
图2 球艏曲线在3个维度上的截面曲线和点的数目与切矢数值Fig.2 The number of curves，points，and angle of end tangent for end points in three dimensions

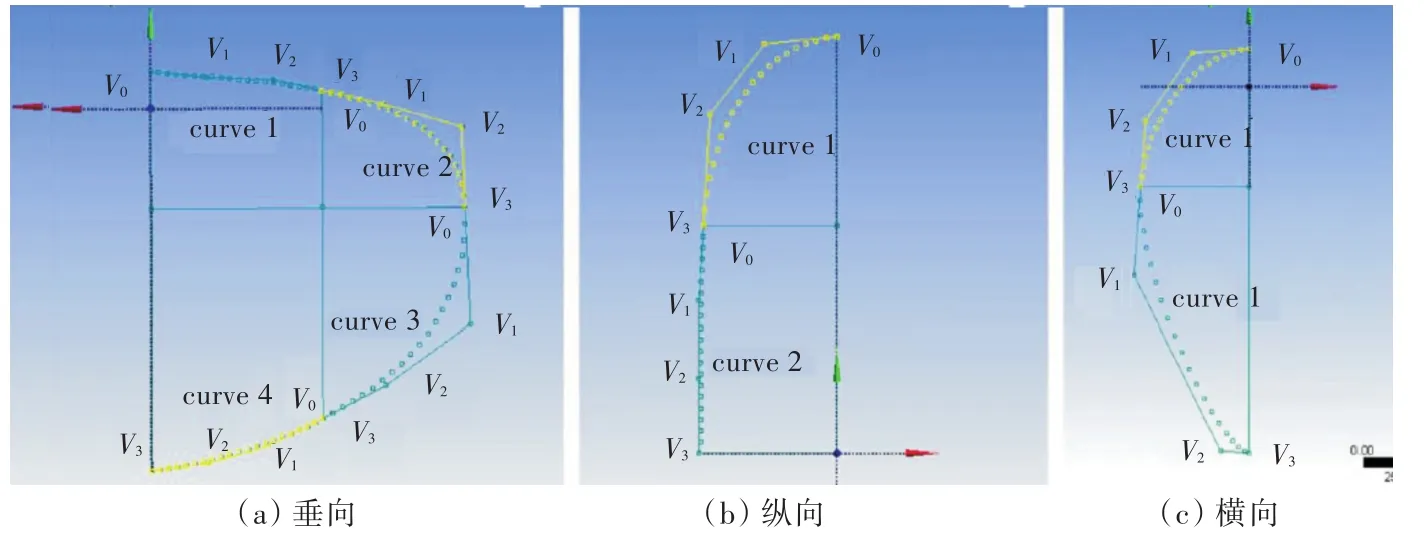
图3 球艏在3个视图的型线分段和定义点示意图Fig.3 Control points and subsection curves of bulbous bow in three planes

其中，所有的曲线分段均取4个定义点，内部定义点V1，V2可根据端点定义点和切矢求出：

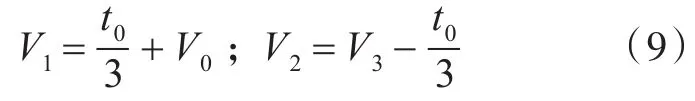
现有的椭圆柱型母型球艏，其横剖面截面长半轴a=0.141 0 m，短半轴b=0.103 5 m，根据文献［2，5］可知，相比重心偏上和居中，球艏重心垂向偏低能够有效改善球艏的阻力性能，即球艏在垂向体积分布的改变会影响球艏船型的阻力特性，因此需进行试算和验证。在进行球艏型线优化的同时，保持原有球艏底部与船底相切的几何特征，不改变球艏纵向等宽可延展部分的长度（球艏前伸量），只对球艏端部和等宽可延展部分的截面形状进行优化。

由于NURBS曲线只取决于定义点而与坐标原点无关，故将球艏单独建模进行构型优化。如图4所示，将球艏在3个维度上进行定义点求取，图4（a）中的线条为原有的型值曲线（数据点曲线拟合），图4（b）中的点为求取的定义点，图4（c）中曲线为利用NURBS方法求取的定义点曲线。经过初步估计，满足曲面生成的精度要求。

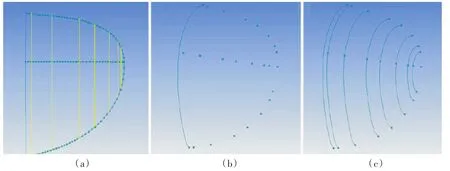
图4 截面曲线定义点反算及曲线生成Fig.4 Procedure of control points calculation on the curve-plane intersection and curves generation

3 基于优化算法的球艏构型优化与效果分析

3.1 利用单纯性算法的定义点优化

单纯性算法（Nelder-Mead simplex algorithm）是一种常用于多维空间中以求解最值为目标函数的数值计算方法，并还应用于导数未知条件下的非线性优化问题中。基于单纯性算法，对球艏进行空间体积分布的优化计算，保证在体积偏移的过程中球艏外形不会产生大的不利变形［10］。对于空间体积分布的偏移，采用调整原型球艏型线中纵切面、横切面和宽度系数最大处的水平切面等3个截面样条曲线定义点的偏移来实现。借助于NURBS理论，为实现在较少输入参数数量的条件下精确控制定义点位置，利用Matlab，在编写的优化算法中引入控制球艏截面面积分布重心的方式。采用调节球艏重心垂向高度来优化球艏横截面形状，亦是探索和尝试球艏垂向体积分布对球艏减阻性能的影响。在实际算法中，将优化构型的几何特征作为算法的约束条件和优化函数，其中包括：

1）球艏横截面积变化小于1%；

2）保证球艏宽度和垂向高度不变；

3）截面积重心偏移量小于5%；

4）保证曲线光顺的约束条件为保证曲线的一阶导数单调变化，二阶导数无拐点。

上述约束条件中，在保证球艏宽度和球艏高度不变的情况下，保证球艏截面积变化较小，即是保证球艏优化前后湿表面积不会变化太大。同时需要注意的是，球艏的重心偏移量不宜过大，否则会产生不必要的几何变形，曲线的光顺也较难实现。

3.2 优化构型的几何生成

图5中的3个图形分别为原型横截面（B31）和2个优化球艏的横截面（B32和B33）图形，其中蓝色曲线为优化定义点曲线，红色离散点为反算所得定义点，绿色曲线为经过插值优化后得到的便于建模的曲线。

根据对经过优化前后所得球艏横截面的对比，从中可以看出曲线有明显的光顺效果。参考文献［11］，对球艏优化前后的构型进行分析，并进行阻力和波形计算。

在球艏横截面优化过程中，球艏的重心发生变化时，球艏的体积分布也随之发生变化，在描述球艏的6个参数中，随之发生变化的只有球艏的深度参数，如表1所示。截面积的变化数量级保持在10-8以下，体积和湿表面积变化也在10-3以下，故可将此类变化忽略不计。

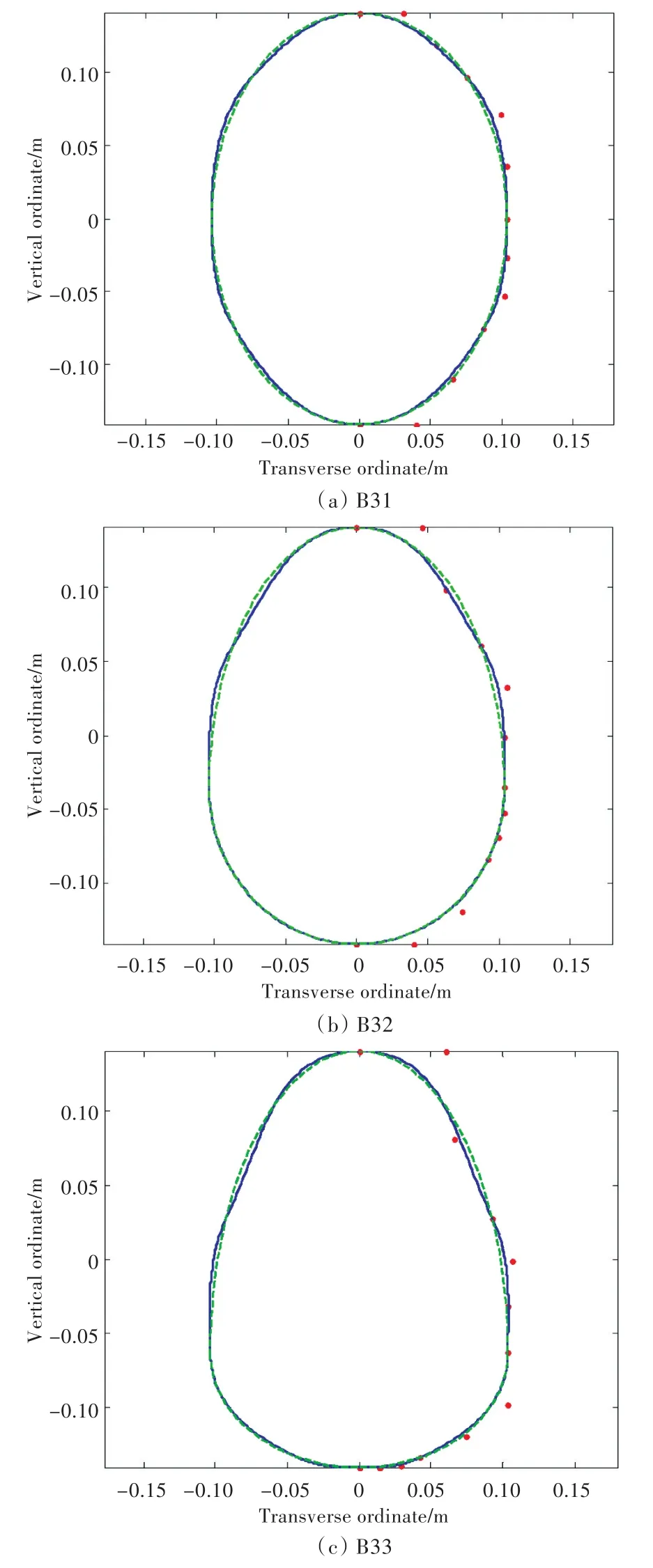
图5 球艏优化前后横截面示意图Fig.5 The crosssection diagrams before and after bulbous bow optimization

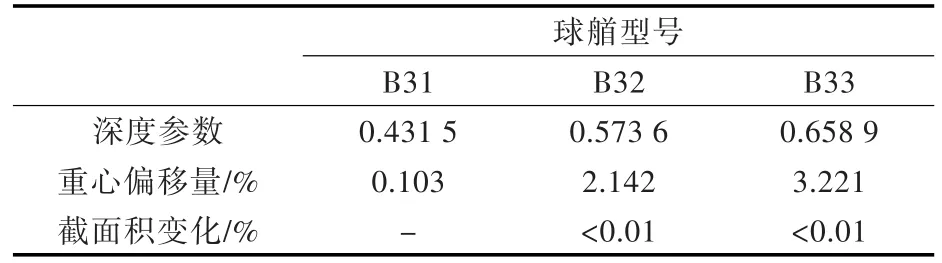
表1 球艏优化前后构型参数对比Table 1 Configuration parameters comparison before and after bulbous bow optimization

如图6和图7所示，对于横切面上下对称的构型B31，其重心的偏移量应为0，表中出现的0.1%的偏移量为样条插值和曲面光顺过程中造成的误差，在实际运算过程中可忽略由此误差造成的影响。同时计算结果显示，在截面积变化不大的情况下，B32湿表面积的相对最大偏差小于1%，B33湿表面积的相对最大偏差小于2.4%，故由此引起的最大摩擦阻力变化小于5%。

图6 优化前后球艏构型图对比Fig.6 Comparison of the oblique view before and after bulbous bow optimization

图7 优化前后球艏侧视图对比Fig.7 Comparison of the side view before and after bulbous bow optimization

3.3 船型阻力和波形计算分析

将球艏加装到削去声呐导流罩的标准船模DTMB 5415进行船型的阻力计算和波形计算［12］。如图8和图9所示，作为改型船，DTMB 5415 31具有一定的减阻效果，但此减阻效果仅限于高速段，因而有一定的改进空间。

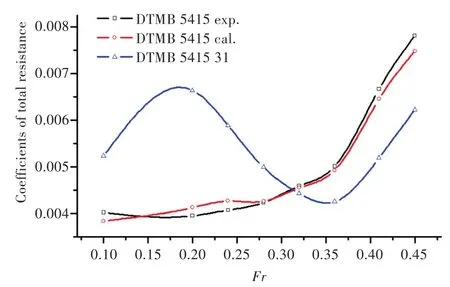
图8 船型DTMB 5415 31与船型DTMB 5415总阻力系数对比Fig.8 Comparison of total resistance coefficients between DTMB 5415 31 and DTMB 5415

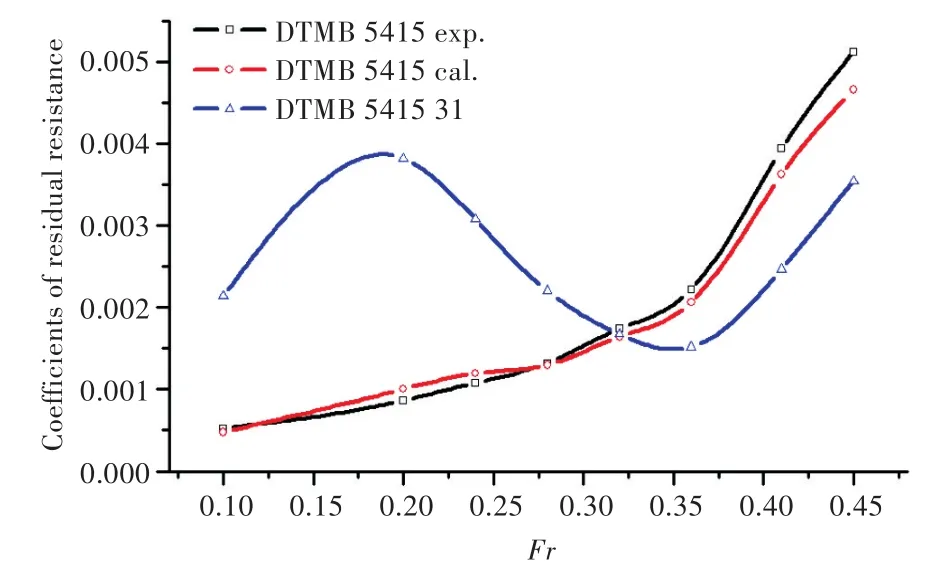
图9 船型DTMB 5415 31与DTMB 5415剩余阻力系数对比Fig.9 Comparison of residual resistance coefficients between DTMB 5415 31 and DTMB 5415

对由构型B31衍生出来的2个球艏B32和B33进行相同的处理，并加装到同样削去了声呐导流罩的标准船模DTMB 5415上，得到相应的球艏船型DTMB 5415 32和DTMB 5415 33。对这2个优化球艏船型进行数值仿真，可得出相应的阻力和波形曲线。将二者的阻力值与DTMB 5415 31进行对比，绘制出相对总阻力系数和相对剩余阻力系数随傅汝德数（Fr）的变化趋势，如图10和图11所示。图12和图13为船体中纵剖面上波形沿船长变化的波形曲线。

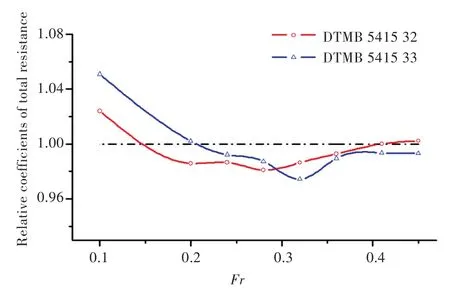
图10 优化球艏船型的相对总阻力系数曲线Fig.10 The relative total resistance coefficient curves of optimization bulbous bow based on B31

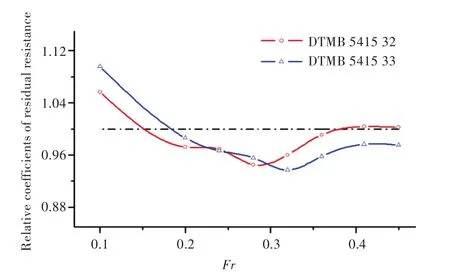
图11 优化球艏船型的相对剩余阻力系数曲线Fig.11 The relative residual resistance coefficient curves of optimization bulbous bow based on B31

图10和图11的结果显示，2个优化球艏在原有球艏基础上构型的微小改变，在中、高速段对船体阻力产生了一定的积极影响。其中，优化球艏B33比B32具有更大的减阻速度区间，且最大减阻幅度也更大，但是B32的减阻速度区间起点更早。

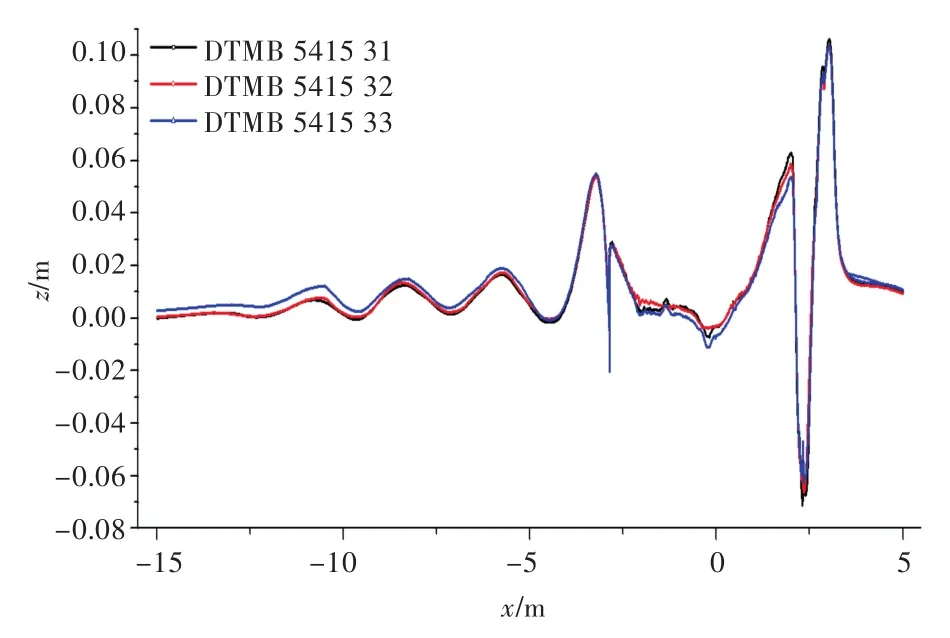
图12 3组球艏模型在Fr=0.28时船体中纵剖面上的波形图Fig.12 Wave profiles of bulbous bow models in central longitudinal section atFr=0.28

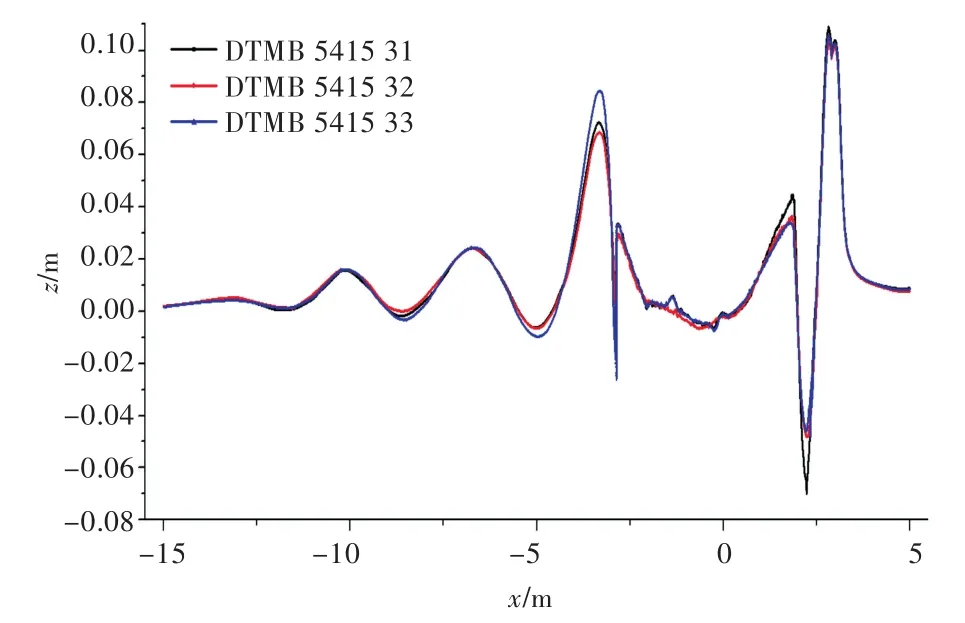
图13 3组球艏模型在Fr=0.32时船体中纵剖面上的波形图Fig.13 Wave profile of bulbous bow model in central longitudinal section atFr=0.32

由图12和图13可看出，在船体中纵剖面波形图中，优化球艏船型的波幅小于初始船型，此种效果在首波系中表现得尤为明显，且改型DTMB5415 33的效果比改型DTMB 5415 32更加明显。

4 结 语

本文运用球艏参数化表达理论，采用NURBS方法对给定型值参数的球艏进行了曲线曲面表达和定义点的反算。利用单纯性算法，结合球艏重心高度对球艏阻力性能影响的规律，目标性地优化球艏形状，并将参数减阻特征直接体现了出来，简化了整个优化过程，取得了预期的减阻效果。

［1］仵大伟，林焰，纪卓尚.船体曲面的NURBS表达与设计［J］.大连理工大学学报，2002，42（5）：569-573.WU D W，LIN Y，JI Z S.Ship hull surface's NURBS representation and design［J］.Journal of Dalian Univer⁃sity of Technology，2002，42（5）：569-573（in Chinese）.

［2］杨凤章.中高速舰船超大型球鼻设计［J］.船舶，1994（1）：22-35.

［3］SHARMA R，SHA O P.Practical hydrodynamic de⁃sign of bulbous bows for ships［J］.Naval Engineers Journal，2005，117（1）：57-76.

［4］PÉREZ F，SUÁREZ J A，CLEMENTE J A，et al.Geo⁃metric modelling of bulbous bows with the use of non-uniform rational B-spline surfaces［J］.Journal of Marine Science and Technology， 2007， 12（2）：83-94.

［5］CHRISMIANTO D，KIM D J.Parametric bulbous bow design using the cubic Bezier curve and curve-plane intersection method for the minimization of ship resis⁃tance in CFD［J］.Journal of Marine Science and Tech⁃nology，2014，19（4）：479-492.

［6］王中，卢晓平.水面舰船加装减阻节能球鼻艏研究［J］.水动力学研究与进展，2006，21（6）：789-795.WANG Z，LU X P.Research on high speed surface warship with bulbous bow［J］.Journal of Hydrodynam⁃ics，2006，21（6）：789-795（in Chinese）.

［7］KRACHT A M.Design of bulbous bows［C］//Paper Pre⁃sented at SNAME Annual Meeting.Jersey：SNAME，1978，86：197-217.

［8］吉贝·德芒热，让皮尔·晡热.曲线与曲面的数学：贝济埃模型、B-样条模型、NURBS模型［M］.王向东，译.北京：商务印书馆，2000.

［9］申玫，林焰，管官.船体NURBS曲线修改方法研究［J］.船舶工程，2009，31（增刊1）：1-3，135.SHEN M，LIN Y，GUAN G.Method for ship hull mod⁃ification of NURBS curves［J］.Ship Engineering，2009，31（Supp 1）：1-3，135（in Chinese）.

［10］MCKINNON K I M.Convergence of the Nelder-Mead simplex method to a nonstationary point［J］.SIAM Journal on Optimization，1998，9（1）：148-158.

［11］VALDENAZZI F，HARRIES S，JANSON C E，et al.The fantastic roro：CFD optimization of the forebody and its experimental verification［C］//Proceedings of NAV2003.Palermo， Italy： Chalmers Publication Library，2003.

［12］张文山，卢晓平.基于圆球型球鼻艏构型的兴波阻力减阻特性分析［J］.中国舰船研究，2017，12（1）：21-26.ZHANG W S，LU X P.Wave-making resistance reduction characteristicsbased on sphericalbow configuration［J］.Chinese Journal of Ship Research，2017，12（1）：21-26（in Chinese）.

NURBS-based parametric optimization and design of bulbous bow

ZHANG Wenshan，LU Xiaoping，WANG Zhong
Department of Naval Architecture Engineering，Naval University of Engineering，Wuhan 430033，China

The well-designed bulbous configuration influences making-waves created by ship，which can be utilized to improve the resistance performance of whole ship，thus the configuration parameters should be optimized.In this research,the data-point mesh generation and control-point calculation of parent-bulb configuration were carried out on the basis of the bulb parametric description and B-spline theory.According to the needs of the optimization,control points were improved to produce a preferable bulb.Next,CFD software was utilized to simulate and calculate models to directly compare the resistance and waveform of the parent-ship to embody the parametric resistance characteristics shown by the orthocenter in the optimization results.The results show that,with the help of B-spline to effectively present the parametric optimization characteristic,the method obtains a vivid and visual pattern,and the efficiency of bow configuration description and optimization is clearly improved.The method simplifies processes of optimization，and the expected goal of resistance reducing has been achieved.

NURBS；wave-making resistance；bow configuration parameter；optimization；CFD

U661.11

：ADOI：10.3969/j.issn.1673-3185.2017.03.003

http://kns.cnki.net/kcms/detail/42.1755.TJ.20170512.1300.036.html期刊网址：www.ship-research.com

张文山，卢晓平，王中.基于NURBS的球艏构型参数优化与分析［J］.中国舰船研究，2017，12（3）：16-22.

ZHANG W S，LU X P，WANG Z.NURBS-based parametric optimization and design of bulbous bow［J］.Chinese Journal of Ship Research，2017，12（3）：16-22.

2016-10-06< class="emphasis_bold">网络出版时间

时间：2017-5-12 13:00

国家自然科学基金青年科学基金资助项目（51609253）

张文山，男，1991年生，硕士生。研究方向：舰船水动力性能。E-mail：zwsrn0706@163.com

卢晓平（通信作者），男，1957年生，博士，教授。研究方向：舰船水动力性能。E-mail：luxiaoping100@163.com

王中，男，1981年生，博士，讲师。研究方向：舰船水动力性能。E-mail：wangzhonghj@sohu.com