“有趣的乘法计算”教学研究报告

一、問题

“有趣的乘法计算———两位数×11”是人教版小学数学三年级下册两位数乘两位数笔算中的一道练习题。我们之所以对一道习题大做文章，是因为运用数的运算规律进行简便计算，是数的运算教学重要的组成部分，既有利于提高学生的学习兴趣，发展数学思维能力，也是培养数感和渗透数学思想方法的重要手段。

在人教版教材的编排中，“两位数×11”是以习题的形式出现（图1），而苏教版教材中则安排为教学专题（图2）。不同教材都是将此内容编排在两位数乘两位数笔算之后，以巩固笔算方法，让学生经历“计算—猜想—分析—验证”的探究过程，积累探索数学规律的活动经验。

在教学实践中，我们发现，学生学过这个知识后不能学以致用，少数学生也只是根据记住的口诀机械地运算，说不清规律和算理。尤其在探索类似数学规律的活动中缺乏自主探究的方法和能力，仅仅满足于表面的规律，不善于探究深层次的原因。

是什么原因导致学生出现这些问题？经过仔细分析，我们认为主要原因如下：一是教师对此类习题的价值挖掘不够，只是把它当做一道巩固练习题，而学生仅仅是记住了口诀，依葫芦画瓢解几道题，停留在表面；二是教师在教学中重口诀“两头一拉，中间相加”、轻算理，没有让学生结合竖式发现规律背后的道理；三是教师把关注点放在得出结论和解题训练上，没有放手让学生自主探索，学生缺乏充分的观察、计算、交流讨论、比较归纳的时间，没有经历探究过程，无法积累数学活动经验。

基于此，我们对“两位数×11”这道习题进行了深度开发，引导学生通过计算、观察、比较、归纳等活动，探索并发现“两位数×11”的计算规律，以丰富对乘法计算过程和特点的认识，并让学生经历探索规律和发现规律的过程，在过程中感受探索性学习的乐趣，积累数学活动经验，培养初步的分析能力和合情推理能力。

二、实践

（一）竞赛置疑，激发兴趣

师：同学们，今天我们将进行一场人机大战，挑战两位数乘两位数的计算，请一个同学用计算器算，我直接口算，其他同学当评委。比赛规则是：屏幕随机出示题目，你们一起喊停，看到题目后我和他同时算，谁最先算出正确答案并大声报出得数就获胜。明白了吗？看屏幕，PK赛正式开始！

屏幕随机出题：第一局：36×11；第二局：65×65；第三局：89×11。

生1：哇，都是老师胜了！

师：我算得比用计算器还快，想知道其中的奥秘吗？今天，我们就一起研究有趣的乘法计算。（板书课题：有趣的乘法计算）

评析：通过人机大战导入新课，学生产生了探索规律的欲望，从而主动参与到学习的活动中。

（二）探索规律，经历过程

师：其实在刚才PK赛的题库中有这样一类题目（课件出示：23×11，54×11，62×11），仔细观察它们有什么共同点？

生2：这3个算式中都有一个因数是11，另一个因数是两位数。

师：观察得真仔细，一下就找到了这类算式的共同特点，都是两位数×11。（板书：两位数×11）这类算式的积有什么秘密呢？请大家用竖式计算，再观察比较每一个算式的积与第一个因数，你有什么发现？请在学习小组内交流你的发现。

学生独立计算、思考，然后进行小组交流。

师：谁来汇报你计算的结果和你们组的发现？

生3：我们计算的结果依次是253、594、682。（课件同步出示竖式及正确答案，如图3所示）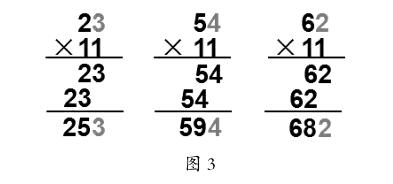

师：观察比较每一个算式的积与第一个因数，你们有什么发现？

生4：我们组发现每个算式的积的个位上的数等于第一个因数个位上的数，积的百位上的数等于第一个因数十位上的数。（对照图3中的竖式一一验证）

师：太厉害了，找到了积的个位、百位上的数的规律。还有别的发现吗？

生5：我们组发现积的十位上的数也有规律，它们等于第一个因数个位和十位上的数的和。

师：真的吗？我们一起算算。（对照3个竖式一一验证，如图4所示）在计算23×11时，为什么个位上的3会和十位上的2相加呢？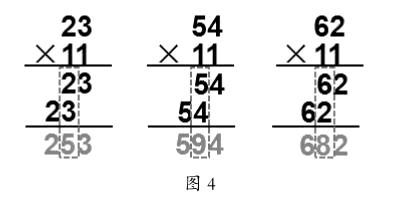

生6：因为个位上的3是去乘第二个因数十位上的1，乘积为3个十，所以与十位上的2相加。

师：听了你的精彩分析，我明白了为什么积的十位会有这样的规律了。还有哪个组想分享吗？

生7：我们组发现每个算式的积其实就是把第一个因数分开，中间加了一个数，这个数就是第一个因数个位与十位上的数之和。（师将他的发现板书：23×11=253，54×11=594，62×11=682）

师：同学们刚才都发现这3个算式的积有共同的规律，积的个位上的数，与第一个因数个位上的数一样。（课件同步闪烁）积的百位上的数，与第一个因数十位上的数一样。（课件同步闪烁）积十位上的数等于第一个因数十位与个位上的数之和。（如图5所示）同学们还用更简洁的语言概括了：把不是11的这个因数两边一拉，中间相加。（板书：两边一拉，中间相加）这是通过观察这3个竖式发现的规律，是不是其他的两位数×11都有这样的规律呢？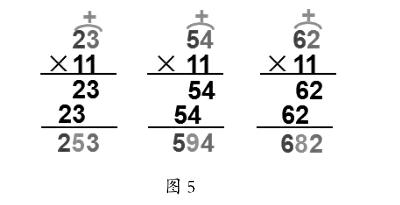

生8：我认为还需要通过举例验证。

师：那好，现在请同桌两人共编一道两位数×11的算式，一人用规律直接写出答案，另一人用竖式计算，看答案是否一致。（课件出示验证活动要求）

学生动手计算并验证。

师：都验证完了，哪组愿意展示一下你们出的题和验证的结果？

生9：我们组出的题是35×11，我用规律“两边一拉，中间相加”写出的得数是385，同桌用竖式计算的得数也是385。符合这个规律。

生10：我们组出的题是68×11，我用规律“两边一拉，中间相加”写出的得数是748，同桌用竖式计算的得数也是748。符合这个规律。

师：68×11=748，积的百位上的数与第一个因数十位上的数不一样了，这是怎么回事？

生11：因为个位上的数与十位上的数相加满十了。当个位上的数与十位上的数相加满十时，就要像竖式计算那样，向百位进一。（板书：满十进一）

师：大家都明白他的意思吗？其他同学验证的结果符合这个规律吗？

学生纷纷点头。

师：祝贺大家经历了观察比较、发现规律、计算验证，探索出了两位数×11的计算规律，数学家们也证明了这个规律是正确的。现在知道我在PK赛中算这类题目获胜的秘诀是什么了吗？

生：知道了，秘诀就是：两边一拉，中间相加，满十进一。

评析：在探究两位数×11的积的规律过程中，学生不仅经历了观察比较、大胆猜想、计算验证等活动，掌握探究计算规律的一般方法，体验到数学的严谨与简洁，还弄清楚了规律背后的道理，获得对规律的深层次理解。

（三）PK大战，应用规律

师：运用规律计算可以算得又对又快。现在你们也来进行一场两位数×11的PK赛。看屏幕，准备出题了！（课件出示：17×11；42×11；53×11；46×11；39×11；11×58）

学生汇报得数，集体订正反馈。

师：在写得数时要注意些什么？

生12：写得数时要注意看是否个位和十位上的数相加满十了，如果满十了就要记得向百位进一。

生13：我建议大家可以先从个位写起，因为不管是否相加满十，积的个位上的数总是等于不是11的这个因数的个位上的数。

师：谢谢大家的提醒。那请继续计算97×11。

学生汇报得数，集体订正反馈。

师：1067，怎么答案不是三位数呢？

生14：因为十位满十，要向百位进一，百位又满十，向千位进一了。

师：哦，我明白了，这道题是出现了连续进位。接下来请解决这道题：□□×11=528。请做得最快的学生回答。

学生动笔计算，不一会就有学生举手。

师：答案是多少？你做得这么快，是怎么想的？

生15：答案是48。我是先看积的个位是8，因为根据规律，积的个位上的数与第一个因数个位上的数一样，所以第一个因数的个位肯定是8；然后看积的百位上的数是5，我以为是58，后来发现58的个位和十位上的数之和的尾数不是2，所以我判断肯定是进位变成5的，原数应该是48。

师：你真是个思维缜密的孩子。他做对了吗？怎么检验？

生16：把48×11用规律算一下看是否等于528，我算了是对的。

评析：在获得规律的基础上，学生自主运用规律进行计算，感受到了数学的神奇和美妙。

（四）回顾反思，拓展延伸

师：同学们，今天的学习你有哪些收获？

生17：我们今天是通过观察一组两位数×11的算式的积与第一个因数，发现了它们具有共同的规律，再通过举例验证其他的两位数×11也符合这个规律，最后总结出两位数×11的计算规律。

生18：我知道了两位数×11的计算规律———两边一拉，中间相加，满十进一。掌握了计算规律，再计算两位数×11，可以算得又对又快。

师：其实数的运算中还藏着很多有趣的计算规律，之前题库中还有两类题目也是有计算规律的。（课件出示图6）大家可以课后尝试找出规律。只要用心观察比较、大胆猜想、计算验证，你就能得到规律。应用规律计算，你也能成为速算高手。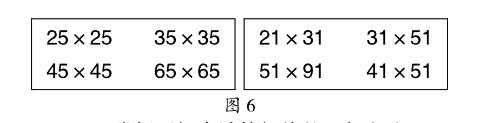

评析：掌握了探索计算规律的一般方法，学生运用该方法可以探索更多的计算规律，将研究延伸到课外。

三、讨论

数的运算是小学数学的重要内容之一，是整个数学教学的基础。但是长期以来，部分教师过分强化了计算技能的训练，以确保计算结果准确无误和计算速度的提高为价值取向，忽视了学生合理、灵活的计算能力的培养，使学生体会不到计算教学的价值。我们认为，在计算教学中应当淡化对运算熟练度的要求，注重培养学生选择正确的计算方法，准确地得到运算结果的能力。这就需要教师在教学的过程中不仅关注计算的方法和结果，更要关注得到方法和结果的思维过程。

1.领悟算理是培养学生运算能力的基础。

算理是指运算中的道理，解决为什么这样算的问题。它是运算的依据，是使学生学会算法的桥梁。要使学生会算，首先必须使学生明白为什么可以这样算，也就是加强算理的理解。在这一课的教学中，教师在学生用竖式正确计算出两位数×11的基础上，通过提出“这类算式的积有什么秘密”“观察比较每一题的积与第一个因数，你有什么发现”等问题，引导学生反思自己的思维过程。学生通过反思，领悟到“每个算式中的积其实就是把第一个因数分开，中间加了一个数，这个数就是第一个因数个位与十位的数之和”。这其实就是两位数×11计算算理的核心。

2.明确算理是培养学生运算能力的关键。

算法是依据算理提炼出来的方法和规则，是解决问题的操作程序。算法使复杂的思维过程得到简化，使运算更加简便、准确。因此在重视理解算理的基础上，还要重视算法的教学，让学生经历探究算法、提炼算法的过程。这节课在探究两位数×11的简便方法时，通过对算式的大胆猜想及课件的动态演示，孩子们逐渐发现：两位数×11，积的个位上的数，与第一个因数个位上的数一样；积的百位上的数，与第一个因数十位上的数一样；积的十位上的数等于第一个因数十位与个位上的数之和。在此基础上，他们初步概括出两位数×11的计算方法是“两边一拉，中间相加”。这个结论只是通过观察3个算式得到的，是否适应所有的两位数×11的算式呢？教师带着孩子们继续验证，最终确认了两位数×11的计算方法。在这一过程中，教师注重引导学生对两位数×11计算方法的探究以及算理的理解，提高了学生的计算意识和计算能力，培养了学生合理、灵活运用计算方法的思维品质。

（本文系湖南省教育科学“十三五”规划一般资助课题《小学数学“三味课堂”研究》階段性成果（课题批准号：XJK016BZXX034））