让学生深度学习
姜湾小学创建于20世纪50年代初。五十余载沧桑砥砺,风雨兼程,姜湾小学从一棵在风雨中摇曳的幼苗成长为枝繁叶茂的大树。十多年来,学校以新课程理念为导向,深入开展“实践新课程,构筑新课堂”活动,对新课程背景下的课堂教学进行了扎实有效的探索。学校数学组全体成员也一直在思考和践行新课程背景下如何让学生深度学习数学,并积累了一些教学经验。
一、促进学生深度学习的教学措施
经过调研,数学组老师们发现,目前,小学数学学习浅层化现象严重,表现在课堂教学形式化,程序化,碎片化,比如凡课必探,凡课必合作学习,课堂生活味浓厚,等等。老师们一致认为,数学深度学习具有理解与批判、联系与构建、迁移与应用三个特点。这意味着,在教学中教师应该引导学生弄清数学知识的来龙去脉、感悟数学思想与方法、构建自身的数学体系,还要将深度延伸至课外。只有这样,才能将数学教学落到实处。
1.引领学生追根溯源,弄清数学知识的来龙去脉。
数学是一门系统性、逻辑性很强的学科,知识之间的联系十分紧密。然而,新课程改革以来,很多老师忽视了数学的这些特性,课堂上热闹非凡,学生却并没有体会到数学的严谨、抽象。这是数学学习浅层化的典型表现。数学组老师们认为,数学教学要消除这些现象,返璞归真,让学生经历数学知识的形成过程,让数学课有“数学味”。因此,教学前,老师们都会查找相关资料,理清新旧知识间的联系,然后做教学法的加工,力图让数学知识自然呈现。
比如,角的度量一课,原来许多老师教学时,总是让学生背口诀(诸如中心对顶点,O线对一边等),然后模仿量角。学生不理解量角原理,自然错误百出。在教学“角的度量”一课时,老师们认为要追根溯源,让学生经历量角器的形成原理,才能正确地量角。因此,教学时,执教老师先在黑板上出示大小明显的∠1和∠2,提问:“除了可以通过观察比较两角的大小之外,还可以怎么比?”在学生用活动角比出大小之后,老师追问:“还有其他方法吗?老师这儿还有些小角(在黑板上贴出若干个10°的木制小角学具),你能用这些小角比较出这两个角的大小吗?”学生的认知平衡第一次被打破,他们带着明确的指向投入到自主活动之中。此问题的解决,让学生比出了两个角的大小,初步形成化整为零的基本思想。“不过这样比还是比较麻烦。能不能想个办法,既保留它的准确性,又改变它操作麻烦的缺点呢?”这一提问驱动学生的思维进一步深入,重新审视并调整自己已建立起来的方法体系,想出“把小角拼起来”“用胶带把小角粘起来”等方法。这时量角器的雏形已经形成。练习题中三个角尤其是∠3的度量,再次把学生带入一种矛盾境地,认知平衡又一次被打破,迫使学生对已经发明的工具加以改进。这时,“可以把每个小角再分成若干個小小角”的想法再次显示了化整为零这一数学思想的威力。随之,“1°角”“把半圆平均分成180份”等量角器的核心要素相继浮出水面。随后,开口方向一右一左的55°角和30°角的度量中,教师精心设计的“怎么才能一眼就看出它的大小呢?”“要是能从图中一下子读出来,那该多好啊!可以怎么办呢?”等问题,使内圈刻度和外圈刻度的呈现水到渠成。
2.让学生获得一些数学思想方法。
数学思想方法是数学的灵魂和精髓,它往往隐含于数学基础知识和解决问题的过程之中。然而,现在许多数学课都只注重教知识,忽视方法的教学和渗透。比如数学广角的教学,许多老师总是希望得出一些公式。这样教学就偏离了轨道,学生自然谈不上深度学习。教学时,如果能充分挖掘教学内容背后的数学思想方法,有意识性地加以渗透,那么,学生所掌握的知识才是鲜活的、可迁移的,学生的数学素养才能得到提升。基于此,数学组老师认为数学思想方法的渗透与数学知识的教学应同步。
(1)备课时把掌握数学知识和学习数学思想方法同时纳入教学目标中,认真钻研教材,不仅要理解知识内容,更要弄清内容中所体现的思想方法。例如,结合认数教学,渗透数形对应,可以设计相应的练习;结合几何公式推导,渗透化归思想等。
(2)掌握数学知识与思想方法的有效结合点,明确每个数学知识应渗透哪些数学思想方法。如解方程渗透了转化思想等。
(3)教学时,应以学生现有的思维发展水平为依据,让学生积极参与整个教学过程,开展主动探索活动,提高学习能力,更好地掌握数学思想方法。
3.让学生构建自身的数学体系。
让学生构建自身的数学体系,这也是深度学习的最终表现。教师作为课堂的主导者,应通过有效的方式方法,引导学生在经历、体验的基础上形成知识体系。
例如,教学人教版五年级上册“梯形的面积”一课时,数学组老师在拓展应用环节设计了如下练习:计算下面图形的面积,你发现了什么?这些图形的面积是否可以用同一个面积计算公式计算?如果能,你认为可以用哪个公式计算?为什么?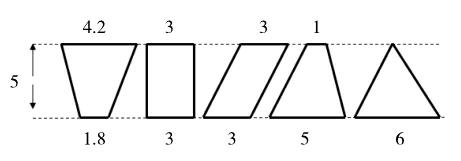
学生通过计算发现这些图形的面积都相等,还发现形状不同的梯形,如果上下底的和与高相等,它们的面积就相等;以上图形的面积都可以用梯形的面积计算公式进行计算。学生通过比较、分析,还发现了:三角形可看作是上底为0的梯形;长方形、平行四边形可看作是上底和下底相等的梯形。
这样教学,学生不仅能深入理解梯形面积的计算公式,还沟通了长方形、平行四边形、三角形和梯形之间的关系,加深了对平面图形特征和面积计算公式的理解,真正透彻理解并建立了平面图形的知识体系。
二、将深度学习延伸至课外
课外作业是小学数学教学的重要组成部分,但传统的课外作业存在着单一性、机械性、重复性、封闭性等弊端,不利于学生的个性化发展。为了突破传统的课外作业模式,将深度延伸到课外,数学组老师们进行了创意作业设计,并在设计的形式、数量、内容上进行改革与创新。
所谓创意作业设计,就是能满足学生个性化特点,具有弹性、生活化的,学生可自主选择、大胆实践、勇于创新的一种课外作业形式。通过创意作业的设计,将学生的深度学习延伸到课外,是我们教学改革的又一新举措。
例如,学习了2、5的倍数的特征和3的倍数的特征后,张晓含同学提出:为什么2和5的倍数只要看个位,而3的倍数要看各位上数字的和呢?是呀!这是为什么呢?孩子们都感到十分好奇。老师抓住这一契机,将其作为当天的创意课外作业,鼓励孩子们课后查找资料,深入思考。课后,刘语菥同学做出了如下解释:比如64是否是2的倍数,我们可以利用原来的知识:A是B的倍数,C也是B的倍数,那么A+C的和也是B的倍数,因为60是2的倍数、4也是2的倍数,所以(60+4)是2的倍数。5也一样,如35,30是5的倍数,5也是5的倍数,那么(30+5)是5的倍数。张晓含同学的解释更是与众不同,她说:一个三位数ABC=100A+10B+C,如果C是2的倍数,假设C=2n,那么100A+10B+C= 100A+10B+2n=2×(50A+5B+n),则这个数一定是2的倍数。从这一解释中可以看出学生思考的深度,这就是将深度学习延伸到课外的成果。
类似这样的创意作业设计,给学生的深度思考拓宽了时空领域,培养了学生深度思考的良好习惯。
经过多年实践,姜湾小学的数学老师们认识到,让学生深度学习,是学生的个体思维从狭隘走向广阔、从肤浅走向深刻必不可少的一种学习方式。学生的学习不仅能识记、理解、应用,更能分析、评价和创造。让学生深度学习,我们将会继续坚持,一路前行!

