Quantum storage of orbital angular momentum states

Shi Bao-Sen*,Ding Dong-Sheng,Zhang Wei

1.CAS Key Laboratory of Quantum Information, University of Science and Technology of China,Hefei,Anhui,230026 2.Synergetic Innovation Center of Quantum Information&Quantum Physics, University of Science and Technology of China,Hefei,Anhui,230026

Quantum storage of orbital angular momentum states

Shi Bao-Sen1,2*,Ding Dong-Sheng1,2,Zhang Wei1,2

1.CAS Key Laboratory of Quantum Information, University of Science and Technology of China,Hefei,Anhui,230026 2.Synergetic Innovation Center of Quantum Information&Quantum Physics, University of Science and Technology of China,Hefei,Anhui,230026

Light carrying orbital angular momentum(OAM)has many exciting applications in the studies of fundamental quantum physics,optical manipulation and trapping of particles,astrophysics,high-precision optical measurements and optical communication both in classical and quantum fi elds,etc.In quantum information fi eld,a photon encoded with information in its OAM degrees of freedom enables networks to carry signi fi cantly more information and increase their capacity greatly due to the inherent in fi nite degrees of freedom for OAM.In order to realize a long-distance quantum communication,quantum repeaters have to be used to overcome the problem of communication fi delity decreasing exponentially with the channel length for,where,quantum memories for photons,used for storing quantum information,are key components of a quantum repeater.So far,there are many works reporting on storing quantum states encoded in for example degree of polarization,path,time bin,etc,however,there have been very few works realizing the storage of OAM states.During the past years,our group has been focusing on the experimental realization of quantum memories for OAM states.In this review, after brie fl y introducing the main benchmarks for quantum memories,we will show a series of important progresses achieved along this research direction in our group,including the storage of OAM qubit and qutrit,of OAM entanglement in a two-dimensional and a high-dimensional space,of hyperentanglement and hybrid entanglement consisting of OAM and other degree of freedom.We believe that all results are very promising for realizing a high-dimensional quantum network in the future.

quantum storage;orbital angular momentum(OAM);quantum memory;atomic ensemble;quantum information

I.INTRODUCTION

It is well known that photons can carry both spin angular momentum(SAM)and orbital angular momentum(OAM).The SAM is related to the polarization. Light with linear polarization carries no SAM,whereas right or left circularly polarized light carries a SAM of ±}per photon.The OAM arises from the helical phase structure in the paraxial regime[1].It was shown by Allen et al.[1]that a photon with a phase form of eilθin the traverse plane carries l}OAM,where θ is angular coordinate and l can be any integer value,positive or negative,respectively.Such beams have helical phase fronts with the number of intertwined helices and the handedness depending on the magnitude and the sign of l[1].OAM light can be described by Laguerre-Gaussian (LG)mode,the normalized wave function of a LG modein the cylindrical coordinates is given by[2]

Where l and p are the azimuthal and radial indexes respectively;w(x)is the beam radius at position x,x is the axial distant from the beam waist;L|l|pis the generalized Laguerre polynomials;k=2π/λ is the wave number.R(x)is the radius of curvature of the beam’s wavefront;φ represents the azimuthal angle;ς(x)is called Gouy phase,which is an extra spatial contribution to the phase.

FIG.1.(color online)Intensity((a),(c))and phase((b), (d))plots of di ff erent LG mode.

Light carrying OAM has stimulated considerable research interest in both classical and quantum optical fi elds,has many exciting applications in for example optical manipulation and trapping[3,4],high-precision optical measurements[5−7],astrophysics[8]and studies of fundamental quantum physics[9−12].Besides,OAM modes with di ff erent l values are orthogonal,which can form a higher-dimensional space.If a photon could be encoded in this high-dimensional space,the information carried by each photon could be increased from a bit to log2d bits,where d is the dimension of the Hilbert space in which the photon is described,in contrast to the case of photon encoded with for example polarization modes,which can only form a two-dimensional space,a photon encoded in such a space only carries a bit information.Therefore encoding a photon with OAM can signi fi cantly increase its information-carrying capability and enlarge the network capacity[13,14],so it is very useful in high-capacity free-space and fi ber optic communications,both in classical and quantum communications.Therefore there is no surprise that many groups and researchers are active in building up a high-dimensional quantum network and many important progresses have been achieved during the past years.

To realize long-distance quantum communication,a quantum repeater has to be used to overcome the problem of communication fi delity decreasing exponentially with the channel length,where,quantum memories for photons,used for storing quantum information,are key components of a quantum repeater.For the establishment of high-dimensional OAM-based quantum network,realizing the quantum storage of di ff erent OAM states including OAM qudit and OAM entanglement is indispensable.Bright light carrying OAM or a spatial structure has been stored in di ff erent physical systems by using di ff erent storage protocols[15−23].Besides,work has begun on storing such light at near single-photon levels[24,25].However,there have been works neither reporting on the storage of a true single photon with OAM nor realizing quantum memories for OAM entanglement in any physical system.Constructing such quantum memories is a big challenge.Our group is devoted to solving the above problems,and achieves several big progresses along this research direction recently:realizing quantum memories for true single photons carrying OAM and for OAM entanglement in cold atomic ensembles[26−30],making a big step towards building up high-dimensional quantum networks.

In this review,we focus on the experimental progresses achieved on the realization of quantum memories in our group recently,review our series of works about the quantum storage of OAM states,including the storage of OAM qubit[26]and qutrit[27],of OAM entanglement in a two-dimensional[28]and in a highdimensional space[29],of hyper-entanglement and hybrid entanglement consisting of OAM and other degree of freedom,such as path or polarization[30].All results are very promising towards to a high-capacity quantum network in the future.

The outlines of paper are as follows:the fi rst section is an introduction,where the main benchmarks and physical systems and quantum storage protocols for quantum memories are brie fl y shown;then we will show how to store OAM qubit and qutrit in the second and the third sections respectively.In section 4,we will show the realization of quantum memories for OAM entanglement in a two-dimensional space;then we will show the progress about the quantum storage of OAM states entangled in a high-dimensional space in the section 5.In section 6,we will show the experimental realization of quantum memories for hyper-entanglement and hybrid entanglement.Finally,we will give close remarks in the last section.

II.BENCHMARKS,PHYSICAL SYSTEMS AND QUANTUM STORAGE PROTOCOLS FOR QUANTUM MEMORIES[31,32]

A.Benchmarks for quantum memories

We brie fl y discuss the required performance criteria for quantum memories.

1. Fidelity.The fi delity measures quantitatively how close the recalled state from memory resembles the input state.The fi delity between two pure states|ϕ⟩and|φ⟩is given by the formula F=⟨ϕ|φ⟩.The fi delity can be also a good measure of“how quantum”a memory is.;

2.Efficiency.The efficiency measures the energy ratio between the recalled and input signals.For an input at single-photon level,it means the success probability of the memory process.

3.On-demand readout.An important requirement of quantum memories for quantum repeaters is the probability to retrieve the signal on demand, i.e.the possibility to determine the storage time after the storage has occurred.This guarantees that the signal attenuation can be improved from original exponential decay to polynomial decay with quantum repeaters.

4.Memory time or time-bandwidth product.The memory time is the time over which the quantum state remains faithfully in the memory.The decoherence inside the memory reduces the storage time and also a ff ects the storage efficiency and fi delity.A more inclusive measure is the timebandwidth product,where the bandwidth refers to the inverse of the input state duration.It describes quantitatively how many logical operations can be done before the quantum memory decoheres.

5.Appropriate working wavelength.The realization of quantum repeaters requires the storage of quantum entanglement at local nodes and swapping the entanglement between adjacent nodes, which can be achieved by combining the two photons from di ff erent nodes intermediately.Therefore,the photon travelling from the node to the location where Bell state measurement is performed is in the low-loss window of optical fi ber is preferred.By this way,the number of repeaters could be reduced signi fi cantly.However this is very hard to be realized in common schemes due to the lack of the accessible atomic levels of the material.

6.Multimode capacity.The rate of quantum com

munication will increase with the number of information carriers that can be processed in parallel,therefore the number of signals which can be stored in parallel inside the memory is also very important.We have to say that all performance criteria shown before cannot be met in a single physical system at present,therefore the development of a quantum memory suitable for quantum repeaters still remains a big challenge.It is fortunate that di ff erent applications have their speci fi c set of requirements,one can choose di ff erent quantum memories according to their goals.

B.Physical systems used for quantum memories

The used physical candidates for quantum memories can be divided into two categories,according to whether they rely on single quantum emitters or large ensembles of particles.Among the quantum memories based on single quanta,one natural candidate is the single atoms in cavities.Another candidate is the individual trapped ions.The third candidate is the nitrogen-vacancy center in diamond.Quantum dot is also regarded as suitable candidates for the quantum memory.Among the ensemble-based candidates,lasercooled atomic ensembles are currently one of the most advanced systems.Hot gasses support memory protocols similar to the ones implemented in cold ensembles, whose room-temperature operation constitutes an important advantage when considering a large-scale implementation of quantum repeaters due to its simplicity.Rare-earth doped solids are good candidates for quantum memories because they take advantage of the long optical and spin coherence times of impurity ions in a crystalline host cooled to cryogenic temperatures.

C.Storage protocols

Quantum memories can be divided into two di ff erent categories according to the scheme used:one is based on the optically-controlled memories and the other is engineered absorption memories.In the fi rst category, an intensity control light beam is used to record and recall the signal.The second category relies on a large inhomogeneous broadening of an optical absorption line, which is structured to produce the desired absorption and resubmission characteristics.There are many protocols for photon storage,including electromagnetically induced transparency(EIT),far o ff-resonant two-photon transitions(Raman scheme),controlled reversible inhomogeneous broadening,atomic frequency combs,photon echo,optomechanical storage and the o ff-resonant Faraday e ff ect.Of which,EIT,far o ffresonant two-photon transitions,optomechanical storage and o ff-resonant Faraday e ff ect schemes belong tothe fi rst category,the others can be classi fi ed into second category.Each protocol has its own advantages and disadvantages,you can choose it according to your requirement and fi nal goal[31,32].

In our series of experiments reviewed here,we use a cold atomic ensemble trapped in a magneto-optical trap(MOT)as the memory media,EIT or Raman schemes as the storage protocols.Cold atoms are the earliest media used for light storage.Very pure gases of alkali atoms are prepared via laser cooling at di ff erent temperature,from a few milikelvins in MOTs to microkelvins in dipole traps and even tonanokelvinsin Nose-Einstein condensates.The trapped cold atoms can be used to implement various protocols.Cold atoms are ideal systems,they o ff er clean platforms that are isolated from the environment,and are also well-controlled.The ground hyper fi ne sub-levels of cold atoms feature long coherence time and thus are excellent candidates as matter qubit acting as memory.Besides,atomic systems are spectroscopically identical, which is critical for direct interface between remotely located quantum nodes through light.EIT-based storing light in atomic ensembles is the fi rst procedure proposed and used to realize a quantum memory,and it is still one of the most promising avenues towards quantum memories[31,32].Raman protocol uses the o ffresonance atomic con fi guration,has the ability to store a short-time pulse and can operate at high speeds.See Refs[31,32]for a review about EIT and Raman protocols.

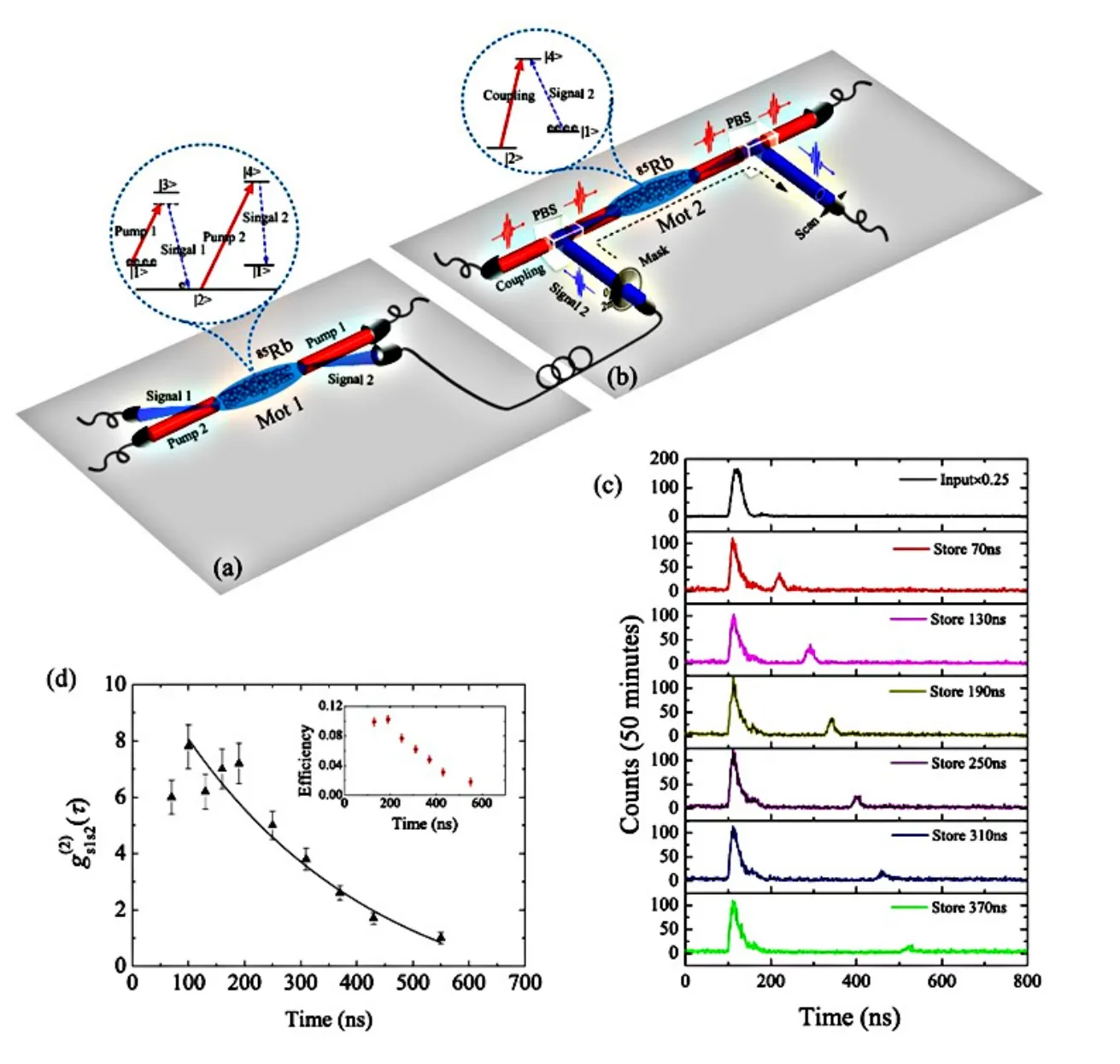
FIG.2.Storage of a single photon.(a)Simpli fi ed diagram depicting the generation of non-classical photon correlations using SFWM.MOT:magneto-optical trap.Inset:energy level diagram for SFWM;(b)Photon storage diagram.PBS:Glan-Taylor polarisation beam splitter with the extinction ratio of 105:1.Inset:energy level diagram for EIT;(c)Coincidence counts between the retrieved signal and the trigger as a function of storage time.(d)Cross-correlation function gs1,s2(τ)between the retrieved signal and the trigger photons against the storage time.The solid line is the exponential fi t Ae−τ/T+g0to(where A=13.3,T=348,g0=−1.89).The inset shows the efficiency function against storage time.All data are raw,without noise correction.Error bars represent±one standard deviation,and are calculated based on the count statistics of single photons.

III.QUANTUM STORAGE OF OAM QUBIT[26]

In this experiment,we prepare non-classical correlated photon pairs using spontaneous four-wave mixing (SFWM)via a double lambda con fi guration in a cold85Rb atomic ensemble trapped in a two-dimensional MOT[33].One photon of each pair is used as a trigger;the other with}OAM is mapped and stored in a second cold atomic ensemble via EIT.After a programmed storage time,the photon is retrieved.We not only prove experimentally that the non-classical correlation between the trigger photon and the retrievedphoton is maintained,but also demonstrate that the spatial structure of the photon is also very well preserved during storage.More importantly,we show with the aid of a Sagnac interferometer that coherence of the single photon is also preserved.

FIG.3.Storage of a true single photon carrying an OAM.(a)Image of a laser beam after traversing the spiral phase plate. The red line is the power distribution curve along the transverse direction.(b)cross-correlation between input signal and trigger photons,obtained by scanning the transverse position of the input signal;(c)cross-correlation function between retrieved signal and the trigger photons.The solid lines in b and c are theoretical fi ts.All data are raw,without noise correction.

In the simpli fi ed experimental setup in Fig.2(a),photon signal 1 at 780 nm is used as a trigger and photon signal 2 at 795 nm is stored for subsequent treatment. We fi rst proved the existence of a non-classical correlation between these two photons by demonstrating a strong violation of the Cauchy-Schwarz inequality[34]. The single-photon property of the signal photon was demonstrated by performing the Hanbury-Brown and Twiss(HBT)experiment on the trigger photon[35,36].A pure single photon has the anti-correlation parameter α=0 and a two-photon state has α=0.5.Therefore α<0.5 suggests the near-single-photon character.Experimentally,we obtained an α value of 0.025±0.005 for the signal photon.

We next stored single photons not carrying any spatial structure via EIT in the second atomic ensemble (see Fig.2(b)).Cross-coincidence counts were measured between the trigger photon and the leaked signal photon and the retrieved signal photon(Fig.2(c)).We also measured the efficiency of storage against storage time (Fig.2(d)).An α value of 0.32±0.08 was obtained for the retrieved signal photon having been stored for about 190 ns,con fi rming clearly that the single-photon nature is preserved during storage.

In our experiment,α changed from 0.025(before storage)to 0.32(after storage),we estimated that the noise from the scattering of coupling contributed about 0.16 to α.More strict fi ltering could reduce this kind of noise further.The remaining contribution to α was mainly from the attenuation of the single photon during the storage,retrieval and the measurement.The noise generated through delayed four-wave mixing process could be negligible due to the large detuning of 3 GHz in our experimental energy level con fi guration and the small optical depth(OD)of the memory[37]in our system.

We inserted a spiral phase plate(VPP-1c,RPC Photonics,transmission coefficient>95%)in the optical path along which the signal photon is transmitted.The signal photon now carried}OAM,showing a donut-shape structure shown in Fig.3(a).After approximately 100-ns storage in MOT 2,the signal photon was retrieved and collected into a single-mode fi ber. We scanned the transverse position of the tip of the receiver fi ber and measured the cross-correlation function between the input signal and the trigger photons, obtaining a donut-shape curve,as shown in Fig.3(b); Fig.3(c)shows the cross-correlation function,also donut-shaped,between the retrieved signal and the trigger photons.To compare Fig.3(b)and(c),we calculated image visibility and similarity. The former is obtained fromwhere gs1,s2,max(gs1,s2,min)are the maximal(minimal)crosscorrelation values,was 0.9 for the input signal and 0.88 for the retrieved signal.We also analyzed the fidelity of the retrieved image by calculating the similaritywhere A and B are the gray-scale matrices of the two images to be compared[22].High similarity means high fi delity.The calculated similarity of the retrieved image was 0.996.

Fig.3 provides clear experimental evidence that an image memory at the true single-photon level can be realized using a cold atomic ensemble,the main features of the image had been preserved during storage.The main noise which reduced the signal-to-noise ratio was from the photon generated through the atomic transition of 5P1/2(F′=3)→ 5S1/2(F=3).Dephasing between the two ground states induced by Earth’s magnetic fi eld had an e ff ect during storage,which shortened the storage time and reduced the storage efficiency.It is theoretically predicted that the efficiency of the EIT-based memory could approach unity in an atomic en-semble at high OD[38].In our experiment,the OD is about 10,so we could improve the efficiency by increasing OD.The storage efficiency can be substantially improved by optimizing the pulse shape to match the EIT bandwidth[39,40].One main issue a ff ecting the retrieved image quality was atomic di ff usion,seen as softening at the edges of the image[39,40].This problem can be solved using a 4-f imaging system that Fourier-transforms the image which is then stored,instead of the image itself, in the atomic ensemble.Thus,di ff usion can be reduced signi fi cantly[15]and the image can be stored for a much long time.

FIG.4.Schematic of the simpli fi ed experimental setup demonstrating coherence of a single photon.λ/2(λ/4):a half-wave plate(a quarter-wave plate).PBS:Glan-Taylor polarisation beam splitter with the extinction ratio of 105:1.

A Sagnac interferometer(Fig.4)is used to store OAM qubit.Using such a con fi guration,two orthogonal polarisations,either forward or backward directed, of an input state were stored in the atomic ensemble. We inserted the two phase plate(VPP-2,RPC Photonics)into the two optical paths and the photon state of the input signal,

With l=2 was prepared for storage.The output state evolves intowith a 45◦rotation after the retrieved signal passes a quarter-wave plate.Next,a half-wave plate rotates the photon polarisation to yield the output state,

Where ÛHWP(θ)is the transformational matrix of the half-wave plate with θ the angle of the fast axis with respect to the vertical axis.The output state can be written:

Here,interference between two terms in equation(4) gives rise to a characteristic pattern comprising four spots.Shifting the relative phase of the two terms causes this pattern to rotate.In our experiment,rotating the half-wave plate shifts the phase,i.e.changing θ continuously.We fi rst used weak coherent light (∼104photons per pulse)as the input signal.We set the angle of the half-wave plate at θ=22.5◦,67.5◦, 112.5◦,and 157.5◦respectively,and using a CCD camera(1024×1024,iStar 334T series,Andor)monitored the spatial shape of the light.The results,given in Fig.5,show theoretical simulations and experimental data are in good accord.In addition,we focused the photons in a single spot into a fi ber and detected these using a photon detector(Avalanche diode,PerkinElmer SPCM-AQR-15-FC).From equation(4),we know that the detected intensity of the interference pattern will vary sinusoidally as sin(4θ)as the plate angle changes. In this experiment,we used the true single photon(signal 2 photon,generated through SFWM in MOT 1) as the input signal.Storage time was programmed at 100 ns.The integrated coincidence counts per second in a 50-ns coincidence window with background noise subtracted showed a clear interference pattern against plate angle(Fig.5)with a visibility of 0.74±0.1,the error being statistical arising mainly from noise from the coupling laser and the multi-photon events.Again, experiment and theory agreed well.The results presented clearly demonstrate that coherence between two di ff erent OAM photon states is preserved during storage.

After our work[26]was published in 2013,a group from Universit´e Pierre et Marie Curie,lead by Laurat reported on a similar work[41],they also realized the storage of OAM qubit in a cold atomic ensemble. What we want to emphasize is that the weak coherent light strongly attenuated to single photon level was used there.After that,this group further realized the quantum storage of the vector vortex beams at the single photon level,demonstrating the preservation of the phase and polarization singularities after retrieved. These results are promising for the applications in classical data processing and quantum information protocols based on vector beams,such as alignement-free quantum communications[42].

IV.QUANTUM STORAGE OF QUTRIT[27]

Refs.[26]and[41]reported on the storage of light at the single-photon level,imprinted with an OAM state;however,the photon was still encoded in a twodimensional space,carrying a qubit information.In 2014,our group made the fi rst step towards the experimental realization of a quantum memory that stores true single photons encoded with a high-dimensional quantum state[27].This stored single photon is a heralded single photon prepared by the way similar to previous section in a cold atomic ensemble.It carried an OAM imprinted through a spatial light modulator (SLM)and is stored in another cold atomic ensemble acting as a quantum memory via EIT.We recon-structed the storage process density matrix of a threedimensional state(qutrit)by quantum process tomography with a fi delity of 85.3%±1.8%using a 4-f imag-ing system,proving the feasibility of storing a qutrit in this kind of memory.Figure 6 shows the simpli fi ed experimental setup.

FIG.5.Storing a superposition state of OAM.(a)Rotated interference patterns at di ff erent angle settings of the half-wave plate(see Supplementary Movie1).The left column represents the experimental angle settingsof the half-wave and the quarter-wave plates.The middle column is the experimental results and the right column is the theoretical simulations;(b) interference pattern of the input signal photon as a function of plate angle;(c)interference of retrieved signal with plate angle.Blue and red lines are fi ts of the sinusoid sin(4θ).The background noise has been subtracted.Error bars represent ±one standard deviation,and are obtained based on the count statistics of single photons.

FIG.6.Simpli fi ed experimental setup.(a)Schematic diagram depicting the generation of non-classical photon pairs using SFWM and the storage of a single photon encoded as a high-dimensional state.MOT:magneto-optical trap; Lens:lens with focus length of 300 mm;FC: fi ber coupler;SLM:spatial light modulator;PBS:polarization beam splitter;λ/2:half-wave plate.Inset:energy level diagrams for SFWM and EIT,respectively;(b)Cross-correlation between the input signal and the trigger.The data were scaled by 0.25.(c)Cross-correlation function between the retrieved signal and the trigger after a programmed storage time.(b) and(c)are obtained without both SLMs.

FIG.7.Reconstructing quantum storage process density matrix.(a)The intensity(left panel of each pair)and the phase(right panel)distributions of the input OAM states. (b)and(c)are the real and imaginary parts of the reconstructed quantum storage process density matrix.λ1−9is a basis set for operators[27].

FIG.8.Storing photonic qutrits.(a)The phase(left panel of each pair)and the intensity(right panel)distributions of the photonic qutrit state|Ψ1>=(|L>−|G>+|R>)/31/2. (b)and(c)are the real and imaginary parts of the reconstructed density matrix of the retrieved photonic qutrit |Ψ1>.(d),(e),and(f)are similar to(a),(b),and(c)but for photonic qutrit state|Ψ2>=(|L>−|G>+|R>)/31/2.

The storing and later release of an input state can be considered as a state transfer process,and represented by a quantum process density matrix χ.The main focus now is to reconstruct this matrix by performing quantum process tomography.We take the storage of a qutrit state as an example.For that,we input one of nine di ff erent states|ψ1−9>corresponding to the states|L>,|G>,|R>,(|G>+|L>)/21/2,(|G>+ |R>)/21/2,(|G>+i|L>)/21/2,(|G>−i|R>)/21/2, (|L>+|R>)/21/2,(|L>+i|R>)/21/2to MOT 2 for storage,respectively,where|L>,|G>,and|R>are states corresponding to a well-de fi ned OAM of 1~,0 and−1~respectively.These input states,having different phases and intensity distributions(see Fig.7(a)) were prepared though SLM1(HOLOEYE,PLUTO,an active area of 15.36 mm×8.64 mm,the pixel pitch size is 8µmand the total pixels are 1920×1080.).The SLM is of re fl ective type with 60%efficiency.After the programmed storage time,the stored state was retrieved and measured in nine di ff erent OAM basis vectors,the same as the nine input states[43].These basis vectors for measurements were prepared by another SLM 2.In addition,a 4-f imaging system was used that was the key in reconstructing correctly the density matrix(see Ref.27 for details.).

By inputting nine input states,measuring each retrieved input state in the nine basis vectors,and then integrating coincidence counts in a 50-ns coincidence window with background noise subtracted in each measurement(the background noise is the coincidence count with no input photon for storage in MOT 2.),we obtained a set of 81 data points and reconstructed the quantum process density matrix for our quantum memory system[44,45].The results are shown in Fig.7(b)and (c).Compared with the ideal quantum storage process density matrix,the fi delity obtained for our density matrix was 85.3%±1.8%.We conclude that our system can store a photonic qutrit.

To further illustrate this storage capability,we performed experiments where we stored two special photonic qutrits|Ψ1>=(|L>+|G>+|R>)/31/2and |Ψ2>=(|L>−|G>+|R>)/31/2as examples.The phase structures and the intensity distributions of these two states are given in Fig.8(a)and(d).By projecting these two states on the nine basis vectors de fi ned before,we obtained the corresponding nine coincidence counts and using them reconstructed the density matrix of the retrieved state,shown in Fig.8(b),(c),(e), and(f).We calculated the fi delities of the reconstructed density matrices by comparing them with the ideal density matrices,obtaining 77%±3%for state|Ψ1>and 80%±2%for state|Ψ2>.

The fi delity of the storage process is below 100%,we believe the main reasons are from various mismatches in the experiments,please see Ref.27.Our method could be extended to reconstruct quantum process density matrices corresponding to high-dimensional OAM states(d≥4).In this case,the big challenge we face in the experimental demonstrations is further improvements in technique,such as how to achieve higher signal-to-noise ratio and how to stabilize the system over long periods.This is because we will have to takemore data.For example,for d=4,256 data points need to be obtained to reconstruct the process density matrix,which require much longer experimental time.

V.QUANTUM STORAGE OF OAM ENTANGLED IN A TWO-DIMENSIONAL SPACE[28]

Refs.[26,41,27]reported on the storage of OAM qubit and qutrit,however,there have been no any experimental progresses for storing entangled OAM states via any protocol in any physical memory system before 2015.In 2015,we reported on the fi rst experimental realization of quantum storage of OAM entanglement in cold atomic ensembles.We establish the OAM entanglement between the anti-Stokes photon and the collective spin excited state of one cold atomic ensemble by spontaneous Raman scattering(SRS) fi rstly[35].Then we send this anti-Stokes photon to and store it via Raman scheme in another cold atomic ensemble acting as the quantum memory.By this way,an OAM entanglement is established between two atomic ensembles. We demonstrate this OAM entanglement by mapping the spin excited states in two ensembles to two photons and checking their entanglement.We prove the entanglement existed in a space consisted of m= ± 1~.We reconstruct the density matrix of the OAM entangled photon pair with a fi delity of 90.3% ± 0.8% and obtain the Clauser,Horne and Shimony and Holt (CHSH)inequality parameter of S=2.41±0.06 after a programmed storage time.All results clearly show the preservation of the entanglement in our memory.

The layout of our experiment was depicted by Fig.9. Pump 1 was applied fi rstly for generating an anti-Stokes photon at 795 nm called signal 1 by a non-collinear SRS process in an optically thick Rb ensemble,which was trapped in MOT1[33].Then the signal 1 photon was delivered into the second MOT 2 for subsequent storage.A coupling pulse laser with orthogonal polarization to signal 1 was used to store the signal 1 via Raman scheme.After the signal 1 photon was retrieved from MOT 2,the pump 2 laser was switched on for converting the collective spin excited state of the atomic ensemble in MOT 1 to a Stokes photon at 780 nm called signal 2.

FIG.9.(Color online)Simpli fi ed energy level diagram of the SRS(a)and setup depicting the storage of entanglement of OAM state.MOT:magneto-optical trap;FC: fi bre coupler;SLM:spatial light modulator;PBS:polarisation beam splitter;λ/2:half-wave plate.

We built up the OAM entanglement between the anti-Stokes photon and the collective spin excited state of the atomic ensemble in MOT 1 speci fi ed by the formula ofwhich is a high-dimensional entangled state.Where subscripts s1 and a1 labeled the signal 1 photon and the atomic ensemble in MOT 1 respectively,|cm|2is the excitation probability,|m⟩is the OAM eigenmode with quanta of m.The initial state of the system has zero linear and angular momentum.Due to the fact that the SRS process conserves momentum,so that the resulting joint state of the anti-Stokes photon and the atomic spin wave has zero total angular momentum,which enforces the OAM correlations between them.After we stored signal 1 photon in the atomic ensemble in MOT 2,an OAM entangled state between two atomic ensembles was established.We demonstrate this OAM entanglement by mapping the spin excited states in two ensembles to two photons and checking their entanglement.In this section we only demonstrated the storage of the OAM entanglement post-selected in a twodimensional subspace(|m>and|−m>basis),thus the photonic entanglement state becomes to be|Ψ>= (|m>|m>+|−m>|−m>)/21/2.Two-qubit state tomography was performed to reconstruct the density matrix of state.We set the delayed time of the applied pump 2 to be 260 ns.Before pump 2 was applied, the OAM entanglement between signal 1 photon and the ensemble in MOT 1 was established,we veri fi ed it by mapping the OAM of the ensemble in MOT 1 to signal 2 photon,and checking OAM entanglement between signal 1 and signal 2 photons.By projecting signal 1 and signal 2 photons on basis vectors of|L>,|R>,(|L>−i|R>)/21/2,(|L>+|R>)/21/2by using two SLMs,we obtained corresponding 16 coincidence rates,then used them to reconstruct the density matrix of the state shown in Fig.10(a)/(b).By using the formula ofwe calculated the fi delity of the reconstructed density matrix by comparing it with the ideal density matrix, which was of 91.0%±1.8%.Where ρidealwas the density matrix corresponding to the ideal OAM entangled state of|Ψ>=(|L>|L>+|R>|R>)/21/2,ρinputwas the reconstructed density matrix.Next we sent the signal 1 photon to MOT 2 for subsequent storage via Raman scheme.After a programmed storage time of 150 ns,the signal 1 was retrieved by switching on the coupling light again.Then we applied the pump 2 to map the spin excited state of the ensemble in MOT 1 to signal 2 photon.We reconstructed the density matrix shown by Fig.10(c)/(d).The fi delity of the density matrix calculated was 84.6%±2.6%by comparing it with the ideal density matrix ρideal,and was 90.3%±0.8%compared with the reconstructed density matrix ρinputbefore storage by using the formula ofwhere ρoutputwas the reconstructed density matrix after storage.

We further characterized the degree of entanglement after storage through checking CHSH inequality[48]:

Where θA,θBwere the angles of the phase distributions on the surfaces of SLMs(see Ref.28).E(θA,θB)can be calculated from the coincidence rates at particular orientations,

We selected θA=0,θB=π/8,θ′A=π/4,θ′B=3π/8. The calculated S was of S=2.48±0.04 before storage and S=2.41±0.06 after storagewith background subtraction(S=2.16±0.04 before storage and S= 2.10±0.06 after storagewithout any background subtraction).The inequality is violated when the values of S are greater than 2 and the violation of inequality means that there exists the entanglement between photons after storage.

Moreover,we checked the two-photon interference. If the visibility of the two-photon interference was> 70.7%[49],then CHSH inequality would be violated, proving the entanglement existed between two photons. We fi xed the phase angle of SLM 1 to be θA=0◦or 45◦respectively,measured the coincidence rate at di ff erent angles of θBof the SLM 2.The storage time was set to be of 150 ns.The experimental results were shown by Fig.11,visibility was 85.2%±3.0%(71.8%±3.3%) at θA=0◦and 86.8%±3.3%(72.9%±3.0%)at θA= 45◦with(without)noise corrections,both were larger than 70.7%,clearly proved the preservation of the OAM entanglement in storage again.

VI.QUANTUM STORAGE OF A HIGH-DIMENSIONAL ENTANGLEMENT[29]

FIG.10.(Color online)The real(a)/(c)and imaginary (b)/(d)parts of the reconstructed density matrix of the state before/after storage respectively.The background noise has been subtracted,which was estimated by repeating the experiment without input signal 1 photon to MOT 2.The measurement time for each data was 500 s in(a)and(b) and 1000 s in(c)and(d).

FIG.11.(Color online)The measured coincidence rate at θA=0◦and 45◦with di ff erent θB.The red(blue)curve represents the correlated coincidence rate with the orientations of θA=0(45◦).The background noise has been subtracted. Error bar is±1 standard deviation.The background noise was estimated by repeating the experiment without input signal 1 photon to MOT 2.The measurement time for each data was 1000 s.

Wehavereported on thecreation ofatwodimensional OAM entanglement between two atomic ensembles[28],but the realization of a high-dimensional entanglement between di ff erent quantum memories is non-trivial,and is not a straightforward extension of establishing a two-dimensional entanglement.There are many challenges,especially in proving the highdimensional entanglement,determining the dimensionality of entanglement,etc.In the following,we reported on the experimental establishment of highdimensional OAM entanglement between two quantum memories in 2014.In our experiment,we entangled high-dimensional OAM states of a photon and a collective spin-excited state in a cold atomic ensemble by SRS[28],and then sent the photon to be stored in another cold atomic ensemble using the Raman protocol.In this way,we established high-dimensional OAM entanglement between two atomic ensembles.We confi rmed the entanglement by mapping the spin-excited states in the two ensembles to two photons and checked their entanglement.We reconstructed the density matrices of the three-dimensional OAM entangled photons.The fi delity of entanglement was calculated to be 83.9±2.9%.We then used an entanglement witness to characterize the nature of the higher dimensional entanglement,concluding that there is at least a four-dimensional entanglement within the two memories.Using the dimensionality witness,we con fi rmed a seven-dimensional entanglement between these two memories.

The experimental media are optically thick atomic ensembles of85Rb trapped in two MOTs[33],separated 1 m apart and working independently.A schematic of the energy levels involved and the experimental setup are shown in Fig.12(a)and(b).The producers for preparing a high-dimensional entanglement between two atomic ensembles,speci fi ed byare the same with the previous section.Where|om|2is the amplitude probability for the di ff erent modes m,and subscript a1/a2 refers to the atomic collective spin-excited state in MOT 1/2.Firstly,we veri fi ed the entanglement with d=3.By projecting the signal-1 and signal-2 photons,retrieved from MOTs 1 and 2,onto SLM 1 and SLM 2,respectively,with nine di ff erent phase states |ψ1−9>de fi ned as the previous section,we reconstruct the density matrix before[Fig.13(a)and(b)]and after[Fig.13(c)and(d)]storage.The di ff erence between the states before and after storage is owing to the di ff erent storage efficiencies for the|R>(|L>) mode and|G>mode[see Ref.29].Using the formulawhere x represents the input and output,ρidealis the density matrix of the ideal three-dimensional OAM entangled state of|Ψideal>= (|R>a1|R>a2+|G>a1|G>a2+|L>a1|L>a2)/31/2, we calculated the fi delity of the reconstructed density matrix before storage and after storage,which were 76.7%±2.8%and 71.7%±2.8%,respectively.Both exceed the threshold of 2/3[43,50]for a maximally entangled state of Schmidt rank 3,i.e.,the Schmidt number of the density matrix must be equal to or greater than 3 before and after storage.All error bars in this experiment were estimated using Poisson statistics and performing Monte Carlo simulations using Mathematica software.We calculated the fi delity of entanglement withwhich gives 83.9%±2.9%.

In principle,the density matrices of the higherdimensional entanglement can be reconstructed using the above method,but the amount of data of order d4needed for a d-dimensional entangled state makes the reconstruction of the density matrix impractical,so we have to seek a di ff erent way to characterize the entanglement.Basically,there are three methods to check whether a system is in high-dimensional entanglement:1)Using unbiased basis states that span the whole subspace[51,52];2)Checking inequalities in higher dimensions directly[53,54];3)Finding a violation that is stronger than allowed within a two-dimensional state space,thereby hinting at entanglement in(untested)higher dimensions.Here,we used method 3 to characterize the entanglement.We used the entanglement witness[55,56]to prove whether there is a high-dimensional entanglement,and the dimensionality witness[57]to characterize the dimensionality of the entanglement.To calculate the witnesses,correlations in three mutually unbiased bases, including diagonal/anti-diagonal,left/right,and horizontal/vertical bases,need to be measured,with the amount of data needed being reduced to 3d(d−1)[60]. The entanglement and dimensionality witnesses can be calculated from the sum of the visibilities M=Vx+Vyand N=Vx+Vy+Vzrespectively,in each 2×2 subspace,where the visibilities are de fi ned as Vi= |⟨σi⊗σi⟩|,i=x,y,z.Here,σx,σy,σzrepresent themeasurements in the three mutually unbiased bases shown above,respectively.The superposition is calculated by adding equal amounts of the two modes and the phase is calculated just from the argument of the resultant complex[61].Figure 14(a)shows an example of mutually unbiased bases formed from the OAM modes m=5 and m= −1.For a separable state within a d-dimensional subspace,a product state of a(d−1)-dimensional maximum entangled state and a single state ψsystem=ψd−1⊗ψ1maximizes the sum of the visibilities.Because the allowed maximum visibility of entanglement in a two-dimensional subspace is 2 (M=Vx+Vy=2,Vx=Vy=1),the allowed maximum visibilities can be calculated as(d−1)(d−2)for a (d−1)-dimensional entanglement.The maximum visibilities for the remaining separable state are(d−1)[56]. Hence,the maximum bound for high-dimensional entanglement is given as:

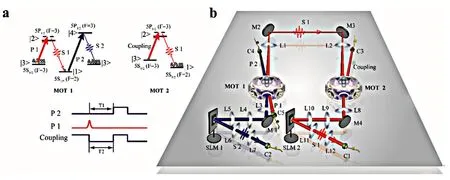
FIG.12.(a)Energy level diagrams and the time sequence for creating and storing entanglement.(b)Experimental setup. Lenses L1 and L2 are used to focus signal 1 on the center of MOT 2.L3,L4,and L5 are used to focus the phase structure of signal 2 on the center of MOT 1 onto the surface of SLM 2.L6 and L7 are used to couple the OAM mode of signal 2 to C2.There is an asymmetric optical path for coupling signal 1 into C1 in the right half of the fi gure.P 1/2:Pump 1/2;S 1/2:Signal 1/2;C: fi ber coupler;M:mirror;L:lens.

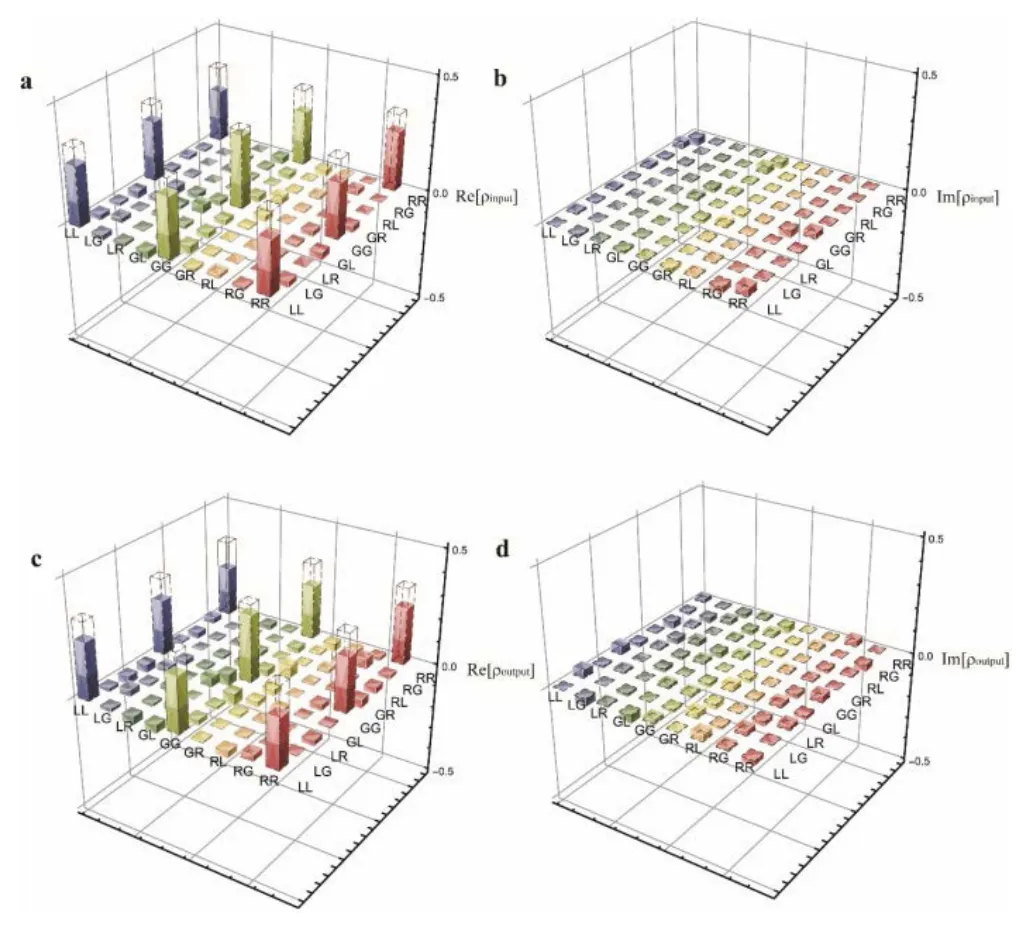
FIG.13.Constructed density matrix of three-dimensional entanglement.(a)and(b)Real and imaginary parts before storage;(c)and(d)those after storage.The dotted bars added in each density matrix correspond to the expected value of the ideal density matrix.

If there is a d-dimensional entanglement,the maximum bound of Mdshould be violated.For a state comprising m=2,1,0,−1,the maximum bound is M4=9.The measured M′is 9.30±0.06 and 9.19±0.06 before and after storage.These values clearly suggest that there is at least a four-dimensional entanglement between these two distant memories.

We also sum the visibilities N for each of the bases to calculate a witness value W to determine the dimensionality of high-dimensional entanglement.All experimentally measured visibilities N are shown in Fig.14(b)and(c),corresponding to quantities before and after storage respectively.The dimensional witness value[62]is given by:

Where D is the number of OAM modes in the measurement.If W>Wdholds,the memories are entangled in at least d+1-dimensions.In our experiment,the measured number of modes is 11(m=−5→ 5);the obtained W of 123.9±0.8 for the input state and 112.8±0.8 for the output state violates the bound of 121 for an input of d=7 and 110 for an output of d=6,both by 3 standard deviations,demonstrating that there exists a seven-dimensional entanglement in our memories.

Ref.63 also reports a quantum storage of a 3 dimensional entanglement in a rare-earth-ion-doped crystal. The properties of the entanglement and the storage process are con fi rmed by the violation of the Bell-type inequality generalized to three dimensions after storage.

VII.REALIZATION OF ENTANGLEMENT IN MULTIPLE DEGREES OF FREEDOM[30]

Acting as information carriers,photons can be entangled not only in a single degree of freedom(DOF), such as in polarization[64],spatial-mode[10],timebin[65]and path[66]entanglement,but also in multiple DOFs independently,as in hyperentanglement[67,68], or in multiple DOFs mutually, as in hybrid entanglement[69].Entanglement in multiple DOFs offers many advantages over entanglement in a single DOF;for example,multi-DOF hyperentanglement enables more efficient Bell measurements[70−72], makes superdense coding that breaks the conventional linear-optics threshold achievable[73,74],and have other applications[13,62,75−78].Alternatively,entanglement in multiple DOFs can exploit the advantages of di ff erent DOFs;for example,photons entangled in the polarization or time-bin DOF can be efficiently transmitted through an optical fi bre,whereas photons encoded in OAM o ff er improved channel capacity in the fi elds of both classical[11]and quantum[26,79]information,so entanglement in multiple DOFs is very promising for quantum networks[42]in terms of enhancing channel capacity and improving compatibility.Such a quantum network requires quantum storage to establish entanglement between di ff erent nodes.Over the past decade, the quantum storage of entanglement in single DOFs has been achieved in many di ff erent quantum memory systems[28,29,80−82];however,the storage of entanglement in multiple DOFs is still a challenge because of the difficulty of simultaneously achieving coherent control of multiple DOFs.Recently,the quantum storage of 2⊗2 hyperentanglement in the polarization and timebin DOFs in a solid memory was reported[83];However,memory-memory entanglement in multiple DOFs,which would represent a critical step towards a multi-DOF quantum network,has not yet been reported. In 2016,our group reported on the realization of the quantum storage of both hyper-and hybrid entanglement in multiple degrees of freedom,including path(K-vector)and orbital angular momentum,between two separated atomic ensembles.Our experimental results demonstrate the successful creation of memory-memory entanglement in multiple DOFs.

FIG.14.(a)The diagonal/anti-diagonal,left/right,and horizontal/vertical bases in the phase and intensity spaces with OAM modes m=5 and m=−1.The superposition is calculated by adding equal amounts of the two modes and the phase is calculated from the argument of the resultant complex[56]with the function Arg(LG5+eiθLG−1),where LG5and LG−1are the amplitudes of OAM states with azimuthal index of 5 and−1,θ represents the relative phase.(b)and(c)are the visibilities before and after storage.The sum of the visibilities in three arbitrary OAM modes of larger than six means the existence of two-dimensional entanglement.

FIG.15.Generation and storage of entanglement in multiple DOFs.(a)Energy diagram and time sequence.Pump 1 and Pump 2 are pulses with durations of∆t1=30 ns and∆t2=200 ns,respectively.The storage time set by∆T for the spin wave in MOT A is 200 ns,and the storage time set by∆t3for the spin wave in MOT B is 100 ns.∆,which represents single-photon detuning,is set to+70 MHz,|1> =|5S1/2,F=2>,|2>=|5S1/2,F=3>,|3>=|5P1/2, F=3>,|4>=|5P3/2,F=3>.(b)Simpli fi ed experimental set-up.PBS:polarizing beam splitter;λ/2:half-wave plate; λ/4:quarter-wave plate;SLM:spatial light modulator;BD: beam displacer;U(D/M/N):represents the path.Pump 1 is obliquely incident on the atomic ensemble with the same angle(1.5◦)with respect to path U and path D in MOT A,and Pump 2 counter-propagates with Pump 1 through the atomic ensemble.The coupling light is also obliquely incident on the atomic ensemble in MOT B with the same angle of 1.5◦with respect to path M and path N.The setup depicted in the region enclosed by the dotted rectangle on the left is used for preparing hybrid entanglement.The powers of the Pump 1,Pump 2,and coupling light beams are 0.1 mW,4 mW,and 24 mW,respectively.

The medium used here to generate entanglement in multiple DOFs is still an optically thick ensemble of85Rb atoms trapped in a 2D MOT.A simpli fi ed illustration of the experimental set-up is presented in Figure 15.Signal 1 photon at a 795-nm wavelength hyperentangled with the spin wave in MOT A is created with the aid of a beam displacer(BD)after illumination with light(Pump1).The BD here is used to coherently superpose the state of Signal 1 from a di ff erent K-vector space to the same path.This hyperentangled state is expressed as shown in Eq.8(hereafter, we use the term “path”to represent the corresponding K-vector throughout the text).Signal 1 photon is then delivered to the second atomic ensemble in MOT B for storage.BD3 and BD4,which form an interferometer,are used to guarantee the same memory efficiency for di ff erently polarized states of the Signal 1 photon. When we shut o ffthe coupling light,the Signal 1 photon is stored in MOT B as an atomic spin wave,thus establishing hyperentanglement between the spin waves of the two atomic ensembles.After a 100ns storage of the spin wave in MOT B and a 200ns storage of the spin wave in MOT A,we retrieve both spin waves to single photons by turning on the coupling light and the Pump 2 light,respectively.Before being collected,both the Signal 1 and Signal 2(retrieved from the spin wave in MOT A)photons are sent to two analysers:a polarization analyser consisting of a polarizing beam splitter (PBS),waveplates,and a SLM.Afterwards,both single photons are fi ltered through cavities(not depicted in Figure 15)and conducted to single-photon detectors through fi bres.We reconstruct the density matrices of the photon-photon states before and after the storage of Signal 1 and check the CHSH inequality to describe the entanglement in the polarization DOF and the OAM DOF.When we exchange the regions surrounded by dotted lines as depicted in Figure 15(b)and simultaneously block the vertical memory path M in MOT B, hybrid entanglement in the path and OAM DOFs between the two atomic ensembles can be experimentally established.

Hyperentanglement,consisting of path-polarization entanglement between a spin wave and a single photon as well as OAM entanglement between a spin wave and a single photon,is directly generated by illumination with Pump 1 through the SRS process in MOT A.The generated state(unnormalized)can be expressed as

FIG.16.Density matrices for hyperentanglement.The real parts of the constructed density matrices for the 2D polarization entanglement(a,b)and the 3D OAM entanglement (c,d),before(a,c)and after(b,d)storage.The values of the imaginary parts of the constructed density matrices are very low;they are distributed in the ranges of 0±4.8% before storage and 0±4.4%after storage for the 2D polarization entanglement and within the ranges of 0±3.5% before storage and 0±5.3%after storage for the 3D OAM entanglement.

where|DA>and|UA>refer to the spin waves related to paths U and D,respectively,in MOT A;|HS1>and |VS1>represent the generated horizontal and vertical polarizations,respectively,of the Signal 1 photon;and θ1is the phase di ff erence between paths U and D,which is set to zero in this experiment.|−mA>represents the OAM eigenmode of the atomic spin wave in MOT A, with quanta of−m,and|mS1>is the OAM eigenmode of the Signal1 photon,with quanta of m.|cm|2is the excitation probability.Here,the value of m ranges from−1 to 1.Usually,cm=c−m.

With the aid of the Mach-Zehnder interferometer formed by BD3 and BD4 and two half-waveplates,the generated Signal1photon that is hyperentangled with the spin wave in MOT A is stored in MOT B.Thus, hyperentanglement between the two atomic ensembles is established as follows:

Where|NB>and|MB>refer to the spin waves related to path N and M,respectively,in MOT B; α=cm=0/cm=1;and cm=1=cm=−1.Hereafter,we use|L>,|G>,and|R>to represent the states|−1>, |0>,and|1>,respectively.After a 100ns storage of Signal 1 in MOT B and a 200ns storage the spin wave in MOT A,we turn on the coupling light and the Pump2 light to retrieve both spin waves to single photons.The resulting photon-photon state can be expressed as

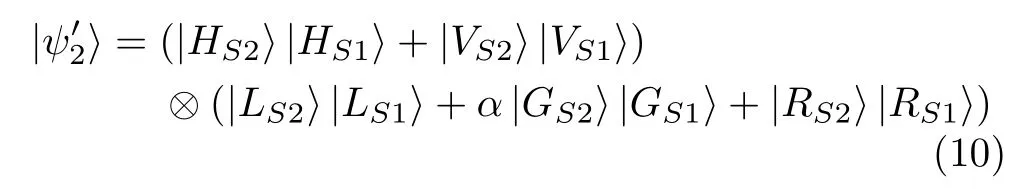
We fi rst reconstruct the density matrices of the photon-photon entanglement in the polarization DOF and the OAM DOF using the standard method[84].For the 2D polarization entanglement,the real parts of the density matrices beforeand afterstorage re shown in Figure 16(a)and(b).For the 3D OAM entanglement,the real parts of the constructed density matrices beforeand afterstorage are shown in Figure 16(c)and(d).

For the 2D polarization entanglement,the fi delity of the polarization-entangled state before storage compared with the ideal state is 87.7± 2.4%,and the fidelity,which quanti fi es how closely the state after storage resembles the state before storage,is 89.7±3.8%. For the 3DOAM entanglement,the corresponding fidelities are 79.7±2.7%and 91.1±4.5%,respectively, where the low fi delity value of 79.7± 2.7%is due to the existence of α,which is equal to∼ 1.1 in our experiment.

Secondly,we demonstrate the entanglement before and after storage by checking whether the CHSH Bell inequality is violated.For the polarization entanglement,we obtain the CHSH parameter SP=2.6± 0.03 before storage and 2.51± 0.05 after approximately100ns of storage time without any noise correction,with θ2=0,θ1=π/8,θ2′=π/4 and θ1′=3π/8. For the 3D OAM entanglement,we check the CHSH inequality in the subspace(listed below)by varying the phase angles of SLM 1 and SLM 2:

Using the same method used in[28],the calculated SOAM−2Dvalues are 2.47± 0.05 before storage and 2.32±0.08 after storage without noise correction.

The average visibilities of interference shown in Fig.17 for the polarization entanglement are 92.4%before storage and 88.4%after storage.For the 2D OAM entanglement,the average visibility is 84.0%before storage and 77.5%after storage.All visibility valuesare larger than the threshold of 70.7%,which clearly proves that entanglement is created and preserved in our quantum memory system.

FIG.17.Interference curves for entanglement.The interference curves before(a,c)and after(b,d)storage,for the 2D polarization(a,b)and 2D OAM(c,d)entanglements.The curves in a and b represent the coincidence rates for di ff erent values of θ1when the Signal2 photon is projected into the states|H>,|V>,(|H>−|V>)1/2,and(|H>+|V>)1/2.The curves in c and d represent the coincidence rates for di ff erent values of θSLM−1when the Signal2 photon is projected into the states|L>,|R>,(|L>−|R>)1/2,and(|L>+|R>)1/2.The error bars are estimated from Poisson statistics and represent ± s.d.

It is obvious from Eq.(8)that the entanglements in the two DOFs are independent of each other.Therefore,a sufficient demonstration of hyperentanglement requires completely independent measurements for every DOF[83]or joint measurements including multiple DOFs[85].However,because of the low count rate of photons in cold atomic media and the di ff erent memory efficiencies between di ff erent DOFs,the ability to employ joint measurements including multiple DOFs is limited because this method requires quite a long measurement time and is subject to low fi delity.Therefore,we adopt the method of measuring entanglement in every DOF independently.Our SLMs are applicable to horizontally polarized light only.The power of the SLMs is shut down when we measure the entanglement between the spin wave and photonic polarization before and after storage;thus,this is a polarizationindependent measurement.However,when we measure the data to construct the density matrices of the 3D OAM entanglement or to check the Bell inequality for the 2D OAM entanglement in the subspace,we must ensure that the photons passing through the SLMs are horizontally polarized,as depicted in Figure 14(b).In this case,the measurement of OAM entanglement is NOT independent of polarization.For completeness,we check the polarization entanglements in the subspace of the OAM DOF to verify the independence.

Another important type of state that takes advantage of multiple DOFs is hybrid entanglement.Whereas hyperentanglement is the entangling of states in multiple DOFs independently,hybrid entanglement is the entangling of states in multiple DOFs mutually.With a small change in the experimental set-up,we can generate polarization-path entanglement between the Signal1 photon and the spin wave in MOT A.Then,using a suitably designed Sagnac interferometer,we convert the photonic polarization information into OAM information.In this way,we establish hybrid entanglement between the photon in the OAM DOF and the spin wave in the path DOF;this state is expressed as |ψ1−hybrid⟩.We input this photon encoded in the OAM DOF into the atomic ensemble in MOT B for storage as a spin wave,thereby establishing hybrid entangle-ment between the two spin waves in the two separated atomic ensembles,which is expressed as|ψ2−hybrid⟩.

To characterize the nature of the hybrid entanglement between the two separated atomic ensembles,we map the state of the spin waves in these memories onto the photonic state(|ψ′2−hybrid⟩)by turning on the Pump 2 and coupling pulse fi elds after 100ns of storage in MOT B and 200ns of storage in MOT A.For entanglement without storage,we turn on only the Pump 2 light to convert this entanglement into photon-photon entanglement(|ψ′1−hybrid⟩),while blocking the coupling light and the ensemble in MOT B.We obtain density matrices for|ψ′1−hybrid⟩and|ψ′2−hybrid⟩through projection measurements,with the results shown(only the real parts)in Figure 18(a)and(b).The related states are expressed as follows:

FIG.18.Density matrices for hybrid entanglement.The real parts of the constructed density matrices for hybrid entanglement before(a)and after(b)storage.The values of the imaginary partsare very low;they are distributed within ranges of 0± 2.9%before storage and 0± 3.8% after storage.

We calculate the fi delity of this entanglement by comparingwith an ideal maximum entangled state,thereby obtaining a value of 94.6±1.4%before storage.After storage,we perform quantum tomography forand obtain the density matrix shown in Figure 18(b).By comparing the density matrices ofandwe calculate the fi delity of hybrid entanglement to be 93.6±1.4%.

At the same time,we measure the two-photon interference to characterize the hybrid entanglement property.The coincidence rates of the two photons are measured in di ff erent bases for Signal 1 and Signal 2.In the bases of(|H>−|V>)/21/2/|H>−i|V>)/21/2for Signal 2,we change the relative phase between|R> and|L>for Signal 1 and obtain the interference curves shown in Figure 19(a)and(b),which correspond to the interference before and after storage,respectively.The average visibility is 93.1%before storage and 84.6%after storage.Both visibility values are larger than the threshold of 70.7%,which is the benchmark for Bell’s inequality,demonstrating that the two memories are truly entangled in these hybrid DOFs.

FIG.19.Interference curves for hybrid entanglement.The interference of the two-photon correlations before(a)and after(b)storage.The error bars are estimated from Poisson statistics and represent± s.d.All the data are raw and notsubjected to noise correction.

We also use an entanglement witness to characterize whether the two memories exhibit hybrid entanglement.The witness is expressed as Where V1and V2are the visibilities of two-photon interference in the diagonal/anti-diagonal and leftcircular/right-circular bases,respectively,of the Signal 2 photon.If there is no entanglement,then the measured witness should not be violated,which would mean that the state is separable.Our experimental results indicate that W=V1+V2=1.861±0.007≫1 before storage and W=V1+V2=1.691±0.025≫1 afterstorage,hinting that there must be hybrid entanglement between our separated memories.

VIII.CLOSE REMARKS

We have realized the quantum storage of a true single photon with OAM and also OAM entanglement,making the fi rst step towards a high-dimensional quantum network.Of course,there are still many basic problems remaining which need to be solved to build the future quantum internet.How to store a qudit(d>3) and a state entangled in a higher dimensional space, especially how to characterize the coherence of the qudit and the entanglement of the high-dimensional entanglement directly determine the possible dimensionality used in quantum networks.Besides,the storage efficiency achieved in all experiments is quite low,the storage time is also quite short,therefore how to improve these important indexes are keys for making the quantum memories applicable in practice.De fi nitely our quantum memories can store a quantum qudit with d>3,but two things need to be considered:1.Achieving the same storage efficiency for di ff erent OAM[27]; 2.Improving and optimizing the experimental system for shortening the experimental period,this is because we have to take more data for a qudit[27].The storage of a two-dimensional entanglement with higher OAM values m/−m could be realized,the storage efficiency decreases with the increase of value m[27],but the fidelity could still keep high.For the storage of a twodimensional entanglement in di ff erent subspaces,the di ff erent storage efficiency for di ff erent OAM will result in low storage fi delity.The larger the OAM value di ff erence is,the worse the fi delity is.So achieving the same storage efficiency for di ff erent OAM is required. This memory could store OAM entangled states in a higher dimensional space in principle:the number of dimension of per photon√ can be simply estimated by the formula of w(z)=m+1w0(z),where,w(z)is the beam waist of a light carrying OAM of m at the center of the atomic vapor in MOT 2,and w0(z)is the beam waist of a Gaussian light.In our experiment, w0(z)100µm,and the radius of the atomic vapor in MOT 2 is∼1 mm,therefore m∼100,i.e.,the maximal OAM dimension of per photon could be stored in our system was limited to be 200.This number is also limited by other factors,such as the Fresnel number and the optical depth of the atomic ensemble[47],the angle of signal fi eld and the control fi eld in MOT 2, etc.,which need further investigation.The storage effi ciency was mainly limited by the reabsorption of the stored photon that was retrieved in the forward direction.Therefore,the maximum efficiency that could be achieved is∼60%.This limitation could be overcome by using a backward direction retrieval,where above 90%efficiency could be achieved[94].The memory time can be improved by compensating the magnetic fi eld or by using magnetic fi eld-insensitive states and reducing atomic motion by using optical lattice,a millisecond even hundred millisecond storage time could be achieved.In addition,the dynamic decoupling method can also be used to improve the storage time.

Anyway, these worksrepresentan important progress,demonstrating that the quantum memories can store di ff erent OAM states,enabling quantum information to be processed at a higher channel capacity. We believe the progresses achieved make an important step for the realization of high-capacity quantum communications.

ACKNOWLEDGMENTS

This work was supported by the National Fundamental Research Program of China(Grant No.2 011CBA00200),the National Natural Science Foundation of China(Grant Nos.11174271,61275115, 61435011,61525504).

REFERENCES

[1]Allen L,Beijersbergen MW,Spreeuw RJC,Woerdman J P.Phys.Rev.A,1992,45:8185-8189

[2]Yao AM,Padgett M J.Adv.Opt.Photonics,2011,3: 161–204

[3]Dholakia K,ˇCiˇzm´ar T.Nat.Photon.,2011,5:335–342

[4]Parterson L,Macdonald MP,Arlt J,Sibbett W,Bryant PE,Dholakia K.Science,2001,292:912-914

[5]D’Ambrosio V,Spagnolo N,Re LD,Slussarenko S,Li Y,et al.Nat.Commun.,2013,4:2432

[6]Lavery MPJ,Speirits FC,Barnett SM,Padgett MJ. Science,2013,341:537-540

[7]Zhou ZY,Li Y,Ding DS,Zhang W,Shi S et al.Opt. Lett.,2014,39:5098-5101

[8]Boyed R W,Townes C H.Appl.Phys.Lett.,1997,31: 440-442

[9]Leach J,Jack B,Romero J,Jha AK,Yao AM,et al. Science,2010,329:662-665

[10]Mair A,Vaziri A,Weihs G,Zeilinger A.Nature,2001, 412:313-316

[11]Fickler R,Lapkiewicz R,Plick WN,Krenn M,Schae ff C,et al.Science,2012,338:640-643

[12]Dada AC,Leach J,Buller G S,Padgett M J,Andersson E.Nat.Phys.,2011,7:677-680

[13]Wang J,Yang JY,Fazal IM,Ahmed N,Yan Y,et al. Nat.Photon.,2012,6:488-496

[14]Bozinovic N,Yue Y,Ren YX,Tur M,Kristensen P,et al.Science,2013,340:1545-1548

[15]Vudyasetu P K,Camacho R M,Howell J C.Phys.Rev. Lett.,2008,100:123903

[16]ShukerM,Firstenberg O,Pugatch R,Ron A,Davidson N.SPhys.Rev.Lett.,2008,100:223601

[17]Wu J H,Liu Y,Ding D S,Zhou Z Y,Shi B S,Guo G C.Phys.Rev.A,2013,87:013845

[18]Ding D S,Wu J H,Zhou Z Y,Shi B S,Zou X B,Guo G C.Phys.Rev.A,2013,87:053830

[19]Heinze G,Rudolf A,Beil F,Halfmann T.Phys.Rev. A,2010,81:011401(R)

[20]Hosseini M,Sparkes B M,Campbell G,Lam P K,Buchler B C.Nature Comm.,2011,2:174

[21]Higginbottom D B,Sparkes B M,Rancic M,Pinel O, Hosseini M,Lam P K,Buchler B C.Phys.Rev.A,2012, 86:023801

[22]Glorieux Q,Clark J B,Marino A M,Zhou Z F,Lett P D.Opt.Express,2012,20:12350-12358

[23]Afzelius M,Simon C,de Riedmatten H,Gisin N.Phys. Rev.A,2009,79:052329

[24]Ding D S,Wu J H,Zhou Z Y,LiuY,Shi B S,Zou X B,Guo G C.Phys.Rev.A,2013,87:013835

[25]Veissier L,Nicolas A,Giner L,Maxein D,Sheremet A S,Giacobino E.Opt.Lett.,2013,38:712-714

[26]Ding D S,Zhou Z Y,Shi B S,Guo G C.Nat.Commun., 2013,4:2527

[27]Ding D S,Zhang W,Zhou Z Y,Pan J S,Xiang G Y, Shi B S,Guo G C,Phys.Rev.A,2014,90:042301

[28]Ding D S,Zhang W,Zhou Z Y,Shi S,Xiang G Y, Wang X S,Jiang Y K,Shi B S,Guo G C.Phys.Rev. Lett.,2015,114:050502

[29]Ding D S,Zhang W,Shi S,Zhou Z Y,Li Y,Shi B S, Guo G C.Light:Sci.&Appl.2016,5:e16157

[30]Zhang W,Ding D S,Dong M X,Shi S,Wang K,Liu S L,Li Y,Zhou Z Y,Shi B S,Guo G C.Nat.Commun., 2016,7:13514

[31]Bussieres F,Sangouard N,Afzelius M,de Riedmatten H,Simon C,J.Mod.Opt.,2013,60:1519–1537

[32]Heshami K,et al.J.Mod.Opt.,2016,63:2005-2028

[33]Liu Y,Wu J H,ShiBS,Guo G C.Chin.Phys.Lett., 2012,29:024205

[34]Kuzmich A,Bowen W P,Boozer A D,Boca A,Chou C W,Duan L M,Kimble H J.Nature,2003,423:731-734

[35]Chanelie‘re T,Matsukevich D N,Jenkins S D,Lan SY, Kennedy T A B,Kuzmich A.Nature,2005,438:833-836

[36]Grangier P,Roger G,Aspect A.Europhys.Lett.,1986, 1:173-179

[37]Chen Y H,Lee M J,Wang I C,Du S W,Chen Y F, Chen Y C,Yu I A,Phys.Rev.Lett.,2013,110:083601

[38]Gorshkov A V,Andr´e A,Fleischhauer M,Sørensen A S,Lukin M D.Phys.Rev.Lett.,2007,98:123601

[39]Phillips N B,Gorshkov A V,Novikova I.Phys.Rev.A, 2008,78:023801(2008)

[40]Zhou S Y,Zhang S C,Liu C,Chen J F,Wen J M,Loy M M T,Wong G K L,Du S W.Opt.Express,2012, 20:24124-24131

[41]Nicolas A,Veissier L,Giner L,Giacobino E,Maxein D, Laurat J A.Nature Photonics,2015,8:234

[42]Parigi V,D’Ambrosio V,Arnold C,Marrucci L,Sciarrino F,Laurat J.Nature Communications,2015,6: 7706

[43]Inoue R,Yonehara T,Miyamoto Y,Koashi M,Kozuma M.Phys.Rev.Lett.,2009,103:110503

[44]Thew R T,Nemoto K,White A G,Munro W J.Phys. Rev.A,2002,66:012303

[45]Chuang I L,Nielsen,M A,J.Mod.Opt.,1997,44: 2455-2467

[46]Grodecka-Grad A,Zeuthen E,and Sørensen A S.Phys. Rev.Lett.,2012,109:133601

[47]Inoue R,Kanai N,Yonehara T,Miyamoto Y,Koashi M,Kozuma M,Phys.Rev.A,2006,74:053809

[48]Leach J,Jack B,Romero J,Ritsch-Marte M,Boyd R W,Jha A K,Barnett S M.Optics Express,2009,17: 8287-8293

[49]Rarity J G and Tapster P R.Phys.Rev.Lett.,1990, 64:2495

[50]Sanpera A,Bruß D,Phys.Rev.A,2001,63:050301(R)

[51]Spengler C,Huber M,Brierley S,Adaktylos T,Hiesmayr B C.Phys.Rev.A,2012,86:022311

[52]Hiesmayr B C,L¨offler W.New J.Phys.,2013,15: 083036

[53]Collins D,Gisin N,Linden N,Massar S,Popescu S.Phys.Rev.Lett.,2002,88:040404

[54]Romero J,Leach J,Jack B,Barnett S M,Padgett M J,Franke-Arnold S.New J.Phys.,2010,12:123007

[55]G¨uhne O,T´othc G.Physics Reports,2009,474:1–75

[56]Fickler R,Krenn M,Lapkiewicz R,Ramelow S, Zeilinger A.Sci.Rep.,2013,3:1914

[57]Bruß D.J.Math.Phys.(N.Y.),2002,43:4237

[58]G¨uhne O,Hyllus P,Bruß D,Ekert A,Lewenstein M, Macchiavello C.Phys.Rev.A,2002,66:062305

[59]Agnew M,Salvail J Z,Leach J,Boyd R W.Phys.Rev. Lett.,2013,111:030402

[60]Agnew M,Leach J,Boyd R W.Eur.Phys.J.D.,2012, 66:156

[61]Franke-Arnold S,Leach J,Padgett M J,Lembessis V E,Ellinas D,Wright A J,Girkin J M,˝Ohberg P,Arnold A S.Optics Express,2007,15:8619–8625

[62]Krenn M,Huber M,Fickler R,Lapkiewicz R,Ramelow S,Zeilinger A.PNAS.,2014,111:6243-6247

[63]Zhou Z Q,Hua Y L,Liu X,Chen G,Xu J S,Han Y J, Li C F,Guo G C.Phys.Rev.Lett.,2015,109:070502

[64]Kwiat P G et al.Phys.Rev.Lett.,1995,75:4337-4341

[65]Brendel J,Gisin N,Tittel W,Zbinden H.Phys.Rev. Lett.,1999,82:2594-2597

[66]Rossi A,Vallone G,Chiuri A,Martini F D,Mataloni P.Phys.Rev.Lett.,2009,102:153902

[67]Kwiat P G.J.Mod.Opt.1997,44:2173-2184

[68]Barreiro J T,Langford N K,Peters N A&Kwiat P G. Phys.Rev.Lett.,2005,95:260501

[69]Schuck C,Huber G,Kurtsiefer C,Weinfurter H.Phys. Rev.Lett.,2006,96:190501

[70]Walborn S P,P´adua S,Monken C H.Phys.Rev.A, 2003.68,042313

[71]Calsamiglia J et al.Appl.Phys.B:Lasers Opt.,2001, 72,67-71.

[72]Barreiro J T,Wei T C,Kwiat P G.Nat.Phys.,2008, 4:282-286

[73]Graham T M et al.Nat.Commun.,2015,6:7185

[74]Nagali E and Fabio S.Opt.Express,2010,18:18243-18248

[75]Gao W B,Lu C Y,Yao X C,Xu P,G¨uhne O,Goebel A,Chen Y A,Peng C Z,Chen Z B,Pan J W.Nat. Phys,2010,6:331-335

[76]Simon C,Pan J W.Phys.Rev.Lett,2002,89:257901

[77]Chen K,Li C M,Zhang Q,Chen Y A,Goebel A,Chen S,Mair A,Pan J W.Phys.Rev.Lett,2007,99:120503

[78]Barbieri M,De Martini F,Mataloni P,Vallone G,Cabello A.Phys.Rev.Lett,2006,97:140407

[79]V´ertesi T,Pironio S,Brunner N.CPhys.Rev.Lett, 2010,104:060401

[80]Choi K S,Deng H,Laurat J,Kimble H J.Nature,2008, 452:67-71

[81]Clausen C,Usmani I,Bussi`eres F,Sangouard N, Afzelius M,de Riedmatten H,Gisin N.Nature,2011, 469:508–511

[82]Saglamyurek E,Jin J,Verma V B,Shaw M D,Marsili F,Nam S W,Oblak D,Tittel W.Nat.Photon,2015, 9:83-87

[83]Tiranov A,Lavoie J,Ferrier A,et al.Optica,2015,2: 279-287

[84]James D F V,Kwiat P G,Munro W J,White A G.Phys.Rev.A,2001,64:052312

[85]Nagali E,Sciarrino F,Martini F D,Marrucci L,Piccirllo B,Karimi E,Santamato E.Phys.Rev.Lett,2009, 103:013601

[86]Surmacz K,Nunn J,Reim K,Lee K C,Lorenz V O, Sussman B,Walmsley I A,Jaksch D.Phys.Rev.A, 2008,78:033806

轨道角动量态的量子存储

史保森1,2，丁冬生1,2，张 伟1,2
1.中国科学院量子信息重点实验室，中国科学技术大学，合肥，安徽，230026 2.量子信息与量子科技前沿协同创新中心，中国科学技术大学，合肥，安徽，230026

轨道角动量(OAM)光束在精密测量、微小粒子的操控以及基础物理研究等领域具有重要的应用。基于OAM编码的光信息处理由于其大信道容量的优点成为经典和量子通信领域的研究热点，并已在近几年取得了许多突破性进展。在量子信息领域，量子中继是克服通信保真度随传输距离呈指数衰减、实现长距离量子通信的关键技术，其中用于存储量子信息的光量子存储器是组成量子中继的关键器件。尽管人们已成功实现了编码于偏振、路径、time bin等自由度的量子态的存储，然而到2013年以前，存储编码于OAM自由度的量子态的量子存储器仍未实现。近年来我们研究组一直专注于OAM量子态的存储实验研究。本文在概述了量子存储器的各项性能标准后，着重介绍我们组在OAM量子态存储方面取得的一系列研究进展：包括OAM量子比特(qubit)和量子三维态(qutrit)、二维和高维OAM纠缠态以及包含OAM自由度的超纠缠和杂化纠缠的量子存储。这些进展为未来构建高维量子信息网络奠定坚实的基础。

量子存储，轨道角动量，量子存储，原子系综，量子信息

1000-0542(2017)3-0098-21

O47 Document Code：A

10.13725/j.cnki.pip.2017.03.002

date:2016-12-06

drshi@ustc.edu.cn