例谈一类数阵图的填法

文︳李艳华

例谈一类数阵图的填法

文︳李艳华

数阵图是一类非常有趣的数学问题，它变化多端，引人入胜，奇妙无穷。许多喜欢探究数字规律的人对数阵图十分着迷，以至有些人留连其中，用毕生的精力研究它的变化。大数学家欧拉对它都有着浓厚的兴趣，数阵图的魅力由此可见一斑。在给学生讲解数阵图的教学中，笔者尝试用浅显易懂的方法，带学生进行了探究。

诸如下面的数阵图，要将所给定的数填入圆圈内，使各线上的数字之和相等，我们无需盲目去套，按下面的方法即可轻而易举地填出。

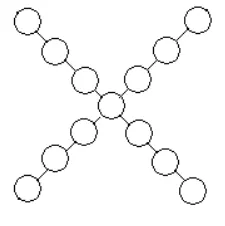
图1 填入1～13

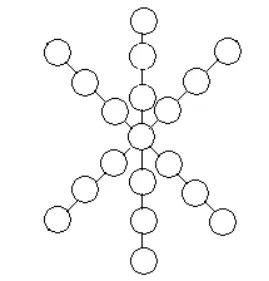
图2 填入1～19

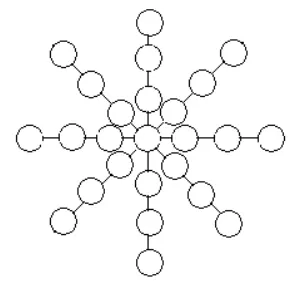
图3 填入1～25

图1：由于1+2+3+…+13＝（1+13）×13÷2＝91，91需减去一个奇数才能被2整除，所以交叉处的可填1，3，5，7，9，11，13，共有7种基本填法。

图2：由于1+2+3+…+19＝（1+19）×19÷2＝190，190需减去1，4，7，10，13，16，19，即减去除以3余1的数才为3的倍数，所以交叉处的可填这7个数，故共有7种基本填法。

图3：由于1+2+3+…+25＝（1+25）×25÷2＝325，325需减去1，5，9，13，17，21，25，即减去除以4余1的数才为4的倍数，所以交叉处的可填这7个数，故共有7种基本填法。

第二步：按如下顺序填入。先填好交叉处的A，再将其他数由小到大按图以B，C，D，E，F…的顺序（似8字形）依次填入即可（如图4、5、6所示）。

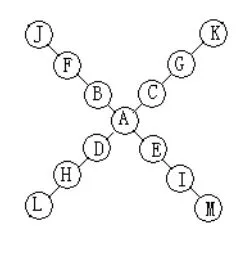
图4

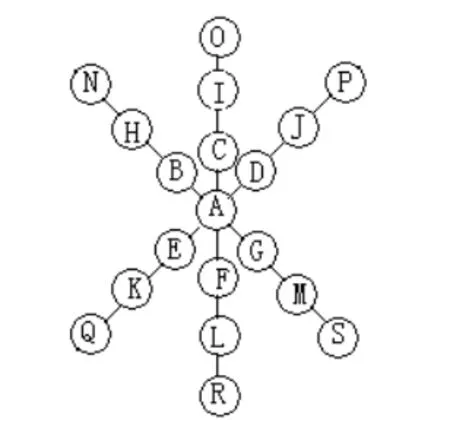
图5

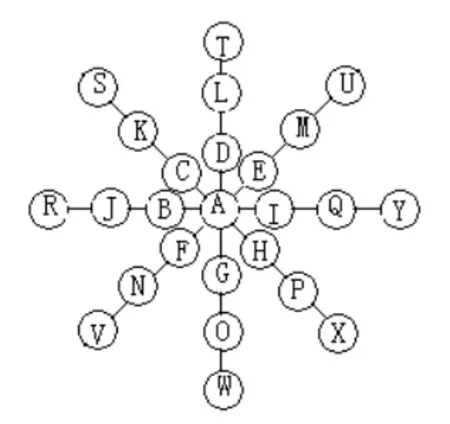
图6

下面给出图4、图5中的A为7，图6中的A为9时的一种填法（如图7、8、9所示）。

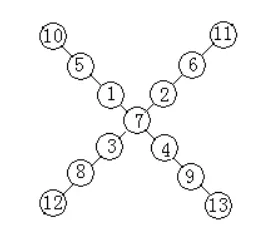
图7

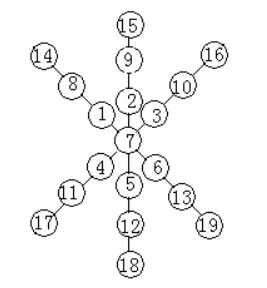
图8

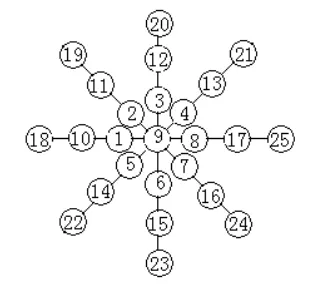
图9

对于这类数阵图，我们还可以得出这样的规律：基本填法的种数与线上的个数相同。

对于图3，如要求三个大的圆上的数之和也要相等，我们需将按上法填好的数进行对调。不过此时的基本填法减少了：因为325减去5，9，17，21时不是3的倍数，亦即交叉处的内只能填1，13，25才能使三个圆上的数之和也相等。具体填法较易，下面仅以13为例填之（如图10所示）。

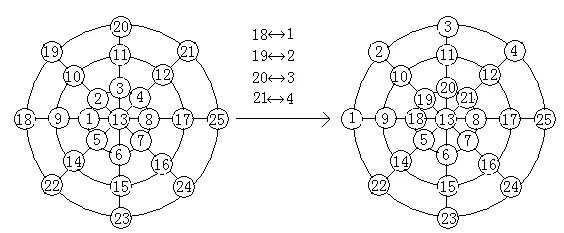
图10

（作者单位：绥宁县民族小学）