走出精讲多练的误区
文︳周自祥
走出精讲多练的误区
文︳周自祥
随着新课改的不断深入,许多教师对精讲多练还存在片面的认识,导致课讲得不细、不透、不深,学生对基本知识理解不透,甚至根本就不理解。那么,教师如何走出理解的误区,实现真正意义的精讲多练呢?
一、精讲不能片面地理解为少讲
一些教师在讲课时,不引入、不探究,直接给出知识点或公式、定理,然后就进行大量的练习。事实上,精讲并非少讲。精讲需要教师在备课时根据教学目标,预设学生学习新知时会遇到的困难,精心设计好问题,在课上引导学生积极主动地进行观察、思考、操作、交流、归纳等。对教材的重点、难点,教师要做到少讲、精讲。精讲要根据知识的难易程度、学生的已有水平等而定。
比如,讲一次函数平移这节课时,可以让学生通过画一次函数图像,从中找到平移的规律。
第一步:学生在平面直角坐标系中画出函数y=x的图像,再将y=x的图像向上、下、左、右分别平移1个单位,然后利用图像与坐标轴的交点确定平移后的一次函数解析式。
第二步:在新的平面直角坐标系中画出y=2x的图像,再将y=2x的图像向上、下、左、右分别平移2个单位,然后利用图像与坐标轴的交点确定平移后的一次函数解析式。
第三步:学生选几个简单的一次函数按以上的步骤画出图像,确定解析式。
第四步:通过观察函数图像与x轴、y轴的交点,学生在教师的引导下总结出函数图像平移时解析式变化的规律。
由于课前教师进行了精心的设计,课堂上师生通过互动对新知进行了总结归纳。学生不仅顺利地掌握了本节课的知识,也为学习二次函数图像的平移打下了良好的基础。
二、注重练习的质量而不是数量
多练是指学生在教师指导下,充分地动口、动手、动脑,进行各种形式的练习活动。设计练习时要充分考虑题目的难度和梯度,应由浅入深、难易适中、逐步提高,突出重点与关键,使学生牢固地掌握知识,培养观察力、思考力和想象力。
练习的形式要多样。教师可以在练习的方式上进行适当的变化。如计算练习时,以小组为单位进行比赛,看哪一组完成得最快;还可以设计成“闯关大比拼”,看谁能最先闯关成功。对于实践操作题,学生可以4人一组进行探讨、交流。对于一些概念题,可以让同桌互相交换着出题。
练习的层次要分明。练习的设计要面向全体学生,注重发展学生个性。教师根据教材内容的需要,精选不同层次的题目,按照不同能力要求编成题组,使思考坡度循序渐进,恰到好处。比如,运用公式法分解因式一节可设计三个层次的练习。
第一层次:基本练习题。
1.下列多项式中,哪些是完全平方式?
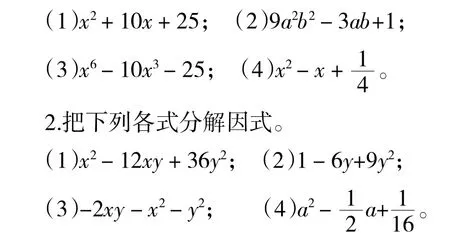
第二层次:提高练习题。
1.将4-12(x-y)+9(x-y)2分解因式。
2.分解因式:-0.25(x+y)2+0.81(x-y)2。
第三层次:深化巩固题。

2.当x取何值时,x2-12x+25取最小值,并求出它的最小值。
注重变式练习。教学时,可以根据教学需要和学生实际情况,设计改变条件或问题与条件同时改变的练习。学生通过练习沟通知识间的内在联系,将知识内化。
(作者单位:新邵县潭溪镇中学)

