找准切入点才能事半功倍
——一道习题的教学思考
文︳袁仁平
找准切入点才能事半功倍
——一道习题的教学思考
文︳袁仁平
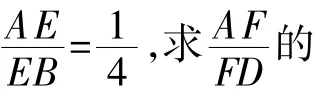
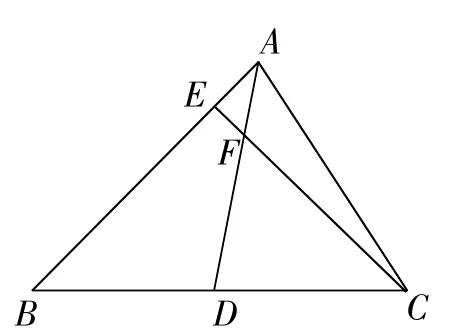
图1
生1:可以求出的值,必须将AF,FD的长度单位统一。

生2:有平行线分线段成比例定理及其推论,还有相似三角形、相似多边形的对应边成比例。
师:不错,我们先看图中有无相似三角形,△AEF和△ABD包含了已知与要求的绝大多数线段,最值得我们关注,但是它们相似吗?
生3:不一定。因为除了公共角相等外,没别的条件了。
师:那怎么办?还有别的三角形吗?
生4:还有△AEF和△CDF,只是也没有充足的理由说明它们相似。
师:的确是这样,图中没有一对三角形是一定相似的。那我们该如何解决呢?
生5:我们可以作平行线构造相似的条件。
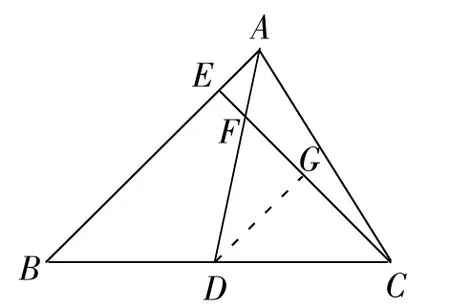
图2
师:是的。平行线可直接或间接得到比例线段。下面我们就过D作DG∥AB交CE于G(如图2),会得到哪些比例线段呢?
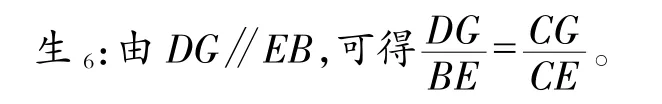
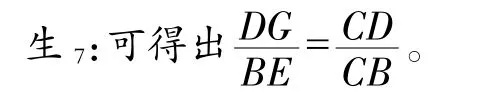
师:这个结论对不对呢?我们一起来分析。因为DG∥EB,所以△CDG△CBE,这是根据平行线分线段成比例定理的推论2,再根据相似三角形的对应边成比例,∠CGD的对边是CD,∠CGD的对应角∠CEB的对边是CB,即可得。因为,所以。你们看,D是BC的中点的条件不就发挥了作用吗?不过我们要求的并不是这个已知条件怎么用上呢?其中的两个比例前项AE与DG之间有何关联?
生8:因为DG∥AE,根据平行线分线段成比例定理的推论2可知△AEF△DGF,再由相似三角形的对应边成比例可得。
师:完全正确。从刚才的学习中我们看到,在作出辅助线之前,已知与未知之间并无明显联系,但作了DG之后,情况完全变了,就好像在已知之间架起了一座桥,加强了它们之间的联系,最终获解。看来作辅助线是关键。下面我再给出一种辅助线的作法(如图3),你们能够求出的值吗?
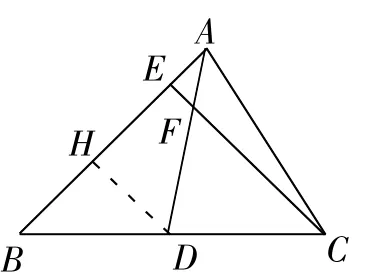
图3
学生动笔求解。教师指名汇报。

师:思路清晰,逻辑严密,很好。那DH与△BCE有什么关系呢?
生:DH是△BCE的中位线。
师:两种辅助线的作法都是作平行线,这样的平行线有什么共同点吗?
生11:都是经过图中的某个交点作某条线段的平行线。
师:观察很细致,但是所作的平行线能否成为连接已知与未知的桥梁和纽带才是最重要的。接下来请同学们尝试作辅助线再求解。
学生纷纷动笔求解,大致有以下几种辅助线的作法。
1.过B作BK∥CE,交AD的延长线于K(如图4)。
2.过C作CL∥AB,交AD的延长线于L(如图5)。
3.过E作EM∥AD,交BC于M(如图6)。
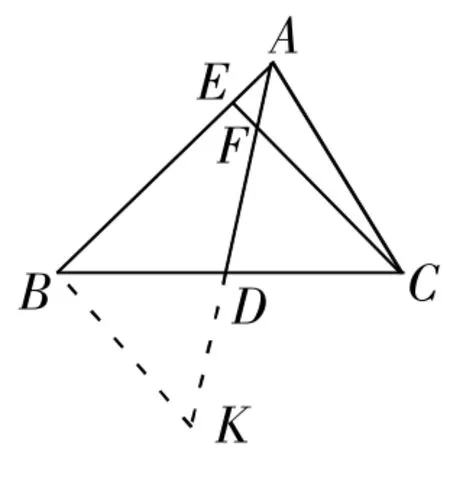
图4
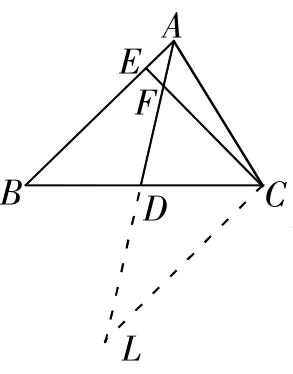
图5
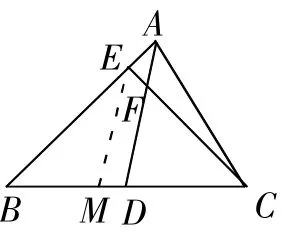
图6
师总结:以上方法都是可行的,值得提出的是,本题都是经过某一交点作某一线段的平行线,但由于辅助线作法的不同,其求解的难易程度也是有很大差异的,有时甚至无法求解。本题的解法还有好几种,只要你大胆尝试、小心求证,一定会有新的收获。本题中的辅助线尽管都是作的平行线,但这并不意味着作平行线是这类题作辅助线的唯一方法,但它的确是一种最基本、最重要的方法。
这是一道经典的习题。由于涉及的知识和方法较多,要想达到预期目标,难度不小。案例中,教师引导学生根据题意找出解题的突破口,当两线段的比值不能直接求出,怎样通过作辅助线构成比例线段,将已知线段比转化为所求线段比,让学生对解决求两线段比值的问题有了比较清晰的思路。
数学习题浩如烟海,在解题教学中,教师的选题要精当,要选取那些有代表性、典型性、针对性、辐射性强的习题,讲深讲透,使学生能够举一反三、触类旁通。习题课教学更重要的是通过解题培养学生的思维。因此,教师在平时要注意积累,才能在教学中发现典型习题,引导学生归纳解题规律,有效地培养学生的解题技能和思维能力。
(作者单位:洞口县五中)

