一个三角形三内角半角余切和不等式的加强——兼擂题(110)的解答

一个三角形三内角半角余切和不等式的加强
——兼擂题(110)的解答

1 背景

在△ABC中，有Kooistra不等式[1]：

(1)

等号成立当且仅当△ABC为正三角形时.

1992年，马统一把这个不等式加强为[2]：

(2)

其中R、r分别为△ABC的外接圆与内切圆半径.

在(2)的形式的启发下，周才凯[3]与宋庆[4]分别进一步证明了更强的结果：

(3)

(4)

(5)

上述不等式即为擂题(110).

2 擂题(110)的证明

只需证

通分后只需证：

∑x5(y+z)+6x2y2z2-xyz∑x2(y+z)-2∑x3y3=

(x+y+z)[∑x4(y+z)+2xyz∑xy-∑x3(y2+z2)-2xyz∑x2]≥0，

即证

∑x4(y+z)+2xyz∑xy-∑x3(y2+z2)-2xyz∑x2≥0，

用增量法，不妨设x≥y≥z，记x=y+u,y=z+v,u、v≥0.

上式展开为：

9z2u2v+2z3v2+2z2v5+2z5u5+4z2u3+2v5u2+3v2u3+2u4z+u4v+2z5vu+8v2u2z+8zu3v+3z2v2u.

因为上述展开式系数全为正，命题得证.

证法2 (山东，张树胜)设R、r分别是△ABC中的外接圆半径，内切圆半径，则

证毕.

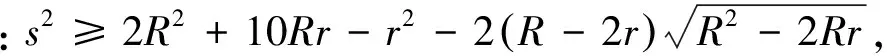
注意到Euler不等式R≥2r,有

从而欲证不等式获证.

3 评注

(点评人，郭要红，2017年5月23日)到目前为止，共收到擂题(110)解答7份，所有解答均是正确的.按时间顺序，作者依次是万惠华(上海，2017年4月19日)，黎建平(四川武胜县，2017年4月20日)，张树胜(山东龙口经济开发区孙家学校，2017年4月21日)，董林(山东高青县教学研究室，2017年4月24日)，严复卓(甘肃省武威市第十八中学，2017年4月26日)，令标(安徽省当涂县青山中学，2017年4月26日)，易桂如(2017年5月20日). 我们刊登其中有代表性的三种风格不同的解答. 本擂题的获奖者是万惠华老师.

1 [荷兰]O.Bottema等著. 几何不等式[M]. 单墫，译. 北京：北京大学出版社，1991

2 马统一. 两个不等式的加强[J]. 中学数学(苏州) 1992(7)：13-14

3 周才凯. 一个三角形不等式的加强及其它[J]. 中学教研(数学)1993(2)：28-29

4 宋庆. 一个三角形不等式的再加强[J]. 中学数学(苏州) 1992(11)：36

5 陈计. 谈一个三角不等式的加强及其它[J]. 中学教研(数学)1993(7)：29-30

6 郭要红. 一个Finsler-Hadwiger型不等式的加强[J].数学通报,2017，56(1): 60-61

有奖解题擂台(111)

文武光华数学工作室褚小光田开斌潘成华

题设Q是△ABC内一点,满足∠QBC=∠QCA=∠QAB=α,P是△ABC所在平面上任意一点,记BC=a,CA=b,AB=c.求证

第一位正确解答者将获得奖金100元.

擂题提供与解答请电邮至guoyaohong1108@163.com，解答认定时间以电子邮件时间为准. 欢迎广大读者踊跃提供擂题.