微研究 让试卷讲评课更有效

安徽省五河县第一中学 (邮编：233300)

微研究 让试卷讲评课更有效

安徽省五河县第一中学张同语(邮编：233300)

试卷讲评课是高三复习教学的重要组成部分，每次考试，总有有些题会让教师和学生都难以释怀，怎么办？我校高三数学备课组的做法是，将一份试卷中大家觉得比较难但又有一定教学研究价值的题选择出来，同一备课组从商讨题目求解、商讨命题意图、商讨试题讲解等三个方面进行微研究.这样做不仅能破解前面的困境，而且能发挥备课组的集体智慧，使得试卷讲评课更加有效.

1 一个案例

图1

(Ⅰ)求直线y=kx+1被椭圆截得的线段长(用a、k表示)；

(Ⅱ)若任意以A(0,1)为圆心的圆与椭圆至多有3个公共点，求椭圆离心率的取值范围.

本题是我校2017届高三年级一道联考试题，选自2016年高考数学浙江卷理科第19题，考后统计发现此题得分率非常低，尤其是第(Ⅱ)问，绝大多数学生因此问涉及的字母多，运算量大而中途放弃.

通过考后访谈，发现多数学生对该题的纠结是：图形中的几何关系如何转化为代数关系；从数值或者方程的不同视角、以及选择不同的解题策略，其运算量差距较大，如何在解题过程中多角度地获取信息、运用信息，进而选择恰当的解题路径是学生的最大障碍.于是，我们高三数学备课组全体老师对此题进行了微研究.

1.1 商讨题目求解

学生在解答问题(Ⅰ)时，困难不大，容易求得直线y=kx+1被椭圆截得线段长

经过商讨，备课组一致认为，为了突破问题(Ⅱ)的解题障碍，通过备课组的集体研究认为，本题的思路可先从题目的条件开始：如何理解“圆与椭圆至多有三个公共点呢？这句话意味着椭圆与圆有0个、1个、2个、3个公共点，也就是说明4个交点的情况不存在，这就暗示我们可从它的反面入手寻找解题的突破口，由此可得：

如果我们在解题时，注意到第(Ⅰ)问的结论，又不难想到另一思路.

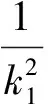
数学需要运算，通过对问题的再认识可缩小运算量，换一个角度，从方程角度思考，我们又可得如下思路.

视角3 (方程思想)：

得(a2-1)y2+2y+r2-1-a2=0，

①

剖析视角3，将问题转化为方程解的问题，使得运算量得以简化，可见，目标的合理确定对运算的路径设计有很大影响，一个合理的运算不仅要求运算是正确的，而且过程也是简捷的.

如果我们将解题视角继续扩大，看看在函数视角下的运算是否更加简捷.

视角4 (函数思想)，设M(x,y)是椭圆上任意一点，连结MA，

则|MA|2=x2+(y-1)2=a2(1-y2)+(y-1)2=(1-a2)y2-2y+a2+1，

剖析从函数角度入手，将问题转化为函数在给定区间上的单调性问题，视角4运算量相对较少，但思维要求较高，真正抓住了问题的本质.

1.2 商讨命题意图

经过商讨，备课组一致认为，本题表面上看是一道常规的解析几何试题，意在考查直线与椭圆的位置关系，数形结合思想、转化化归思想、以及学生运算能力.同时还可以看出，高考对运算能力的考查是分“层次”的，准确、熟练是基本要求，运算的技能要过关，重点是“合理”，根据具体条件合理确定运算目标，设计运算路径，在可能的情况下，利用概念、法则和教学思想方法得到“简捷”的路径.高考考查运算能力，不是进行繁难的运算，而是通过增加思维考核深度，让考生去想怎么算，因为运算素养的关键是“想”不是“算”.因此，本题考查的重点不在知识上，而在思维能力、数学素养上，思维的深度决定视角的宽度.

1.3 商讨试题讲解

备课组全体成员认为， 试题讲解须有界，把哪种解法拿进课堂，拿几种，则应该由教学要求和学生水平来决定.不能教师知道多少种解法就教学生多少种，佳肴虽好，若不顾吸收能力，贪吃无度，则影响健康，适得其反，解法虽多，若不顾学生认知实际，全盘传授，则一厢情愿，广种薄收.

本题的几种思路视角，虽然决定了方法的优劣与运算的繁简程度，但就教学价值而言，前三种思路学生更易接受，思路1，思维起点低，入口宽，学生易于接受.思路2，因其对解题过程相对深入和全方位的思考，对解答高考题具有普遍性的指导意义.思路3思维切入自然，将问题转化为方程根的分布问题目标合理，运算量不大值得重点讲解，思路4思维层次很高，思维切入点隐而难求，且方法的迁移性不强，因而不适合以班级为单位的集体教学，可针对部分学科基础好，思维能力强的学生进行扶优教学.

2 点滴思考

2.1 试卷讲评课，要走集体备课路线

在试卷讲评课之前，通过微研究，加强同一备课组教师间的业务交流，充分发挥集体智慧，其目的是提高试卷讲评课的有效性，同时也能提高数学教师的基本技能，促进备课组成员的共同成长.

2.2 重视题目的选择，让微研究更具针对性

微研究，题目的选择很重要，要尽量选择当次考试中师生求解都相对比较困难，导向性好，具有一定研究价值的问题，为此，最好在集体阅卷完成后，由全组成员共同来确定.

开展微研究，能将题目求解、命题意图、试题讲解有机结合起来，教师通过对题目的分析与研究，对改进教学方法、提高讲评效果、提升教师自身素养是有帮助的.教师的专业成长关键在于自身素养的提高，而备课组是学校最基层的业务组织，那么就让我们从备课组所开展的微研究活动开始吧！

2017-04-08)