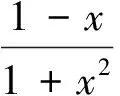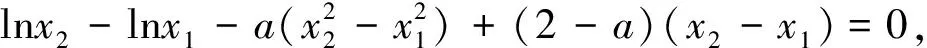函数极值点偏移问题的三种求解策略

湖北省阳新县高级中学 (邮编：435200)

函数极值点偏移问题的三种求解策略

湖北省阳新县高级中学邹生书(邮编：435200)

极值点偏移问题是高考和模拟考的一大热点问题，这类试题设问新颖、综合性强，难度较大.主要考查数学思想方法和运算求解能力，考查推理论证能力以及分析问题和解决问题的能力，同时考查综合素质和数学素养.下面先介绍极值点偏移问题的背景，然后通过典型试题介绍这类问题的三种求解策略.

1 极值点偏移问题的提出

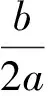
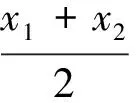
2 极值点偏移问题的求解策略

2.1 构造对称差函数策略

例1 (2010年高考天津卷理科第21题改编)已知函数f(x)=xe-x(x∈R).

(I)求函数f(x)的单调区间和极值；

(II)如果x1≠x2，且f(x1)=f(x2)，证明x1+x2>2.

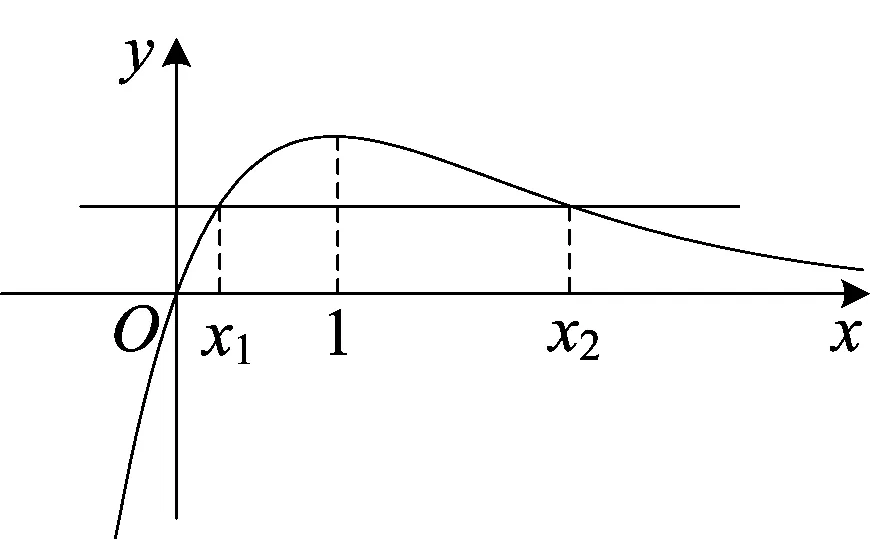
图1

解(I)f′(x)=(1-x)e-x，当x<1时，f′(x)>0，f(x)单调递增；当x>1时，f′(x)<0，f(x)单调递减.所以函数f(x)的单调增区间为(-,1)，减区间为(1,+)，当x=1时函数f(x)有极大值f(1)=，函数没有极小值.

(II)若x1≠x2，且f(x1)=f(x2)，则x1,x2是直线y=f(x1)与函数f(x)的图象两个交点的横坐标，不妨设x1

要证x1+x2>2，只要证x2>2-x1，又02-x1>1.由(I)知f(x)在x>1时递减，故只要证f(x2)

构造函数h(x)=f(x)-f(2-x)，又f(x)=xe-x(x∈R)，所以h(x)=xe-x-(2-x)ex-2，h′(x)=(1-x)(e-x-ex-2)，当00，从而h(x)递增，所以h(x)

故x1+x2>2.

(I)求函数f(x)的单调区间；

(II)证明：当f(x1)=f(x2)(x1≠x2)时，求证x1+x2<0.

2.2 构造增量函数策略

(1)构造差值增量函数

例2 (2014年江苏省南通市二模第20题)设函数f(x)=ex-ax+a(a∈R)，其图象与x轴交于A(x1,0),B(x2,0)两点，且x1

设x2-x1=2t，则只要证当t>0时，2tet0.设g(t)=e2t-2tet-1，则只要证当t>0时，g(t)>0.因为g′(t)=2et(et-t-1)，设h(t)=et-t-1，则h′(t)=et-1，当t>0时，h′(t)>0，所以h(t)递增，所以h(t)>h(1)=0，所以g′(t)>0，所以g(t)递增，所以g(t)>g(1)=0.

(2)构造比值增量函数

例3 (2011年高考辽宁卷理科第21题改编)已知函数f(x)=lnx-ax2+(2-a)x.

(I)讨论f(x)的单调性；

(II)若函数f(x)的图象与x轴交于A、B两点，线段AB中点的横坐标为x0，证明：f′(x0)<0.

因为f(x1)=0,f(x2)=0，所以

(1)试猜测L(a,b)，A(a,b)，G(a,b)这三个数的大小关系.(不需要证明)

(2)若函数g(x)=ex-ax+a存在两个不同的零点.x1,x2(x14,x1+x2>x1x2.

(2)由f(x)=ex-ax+a，得f′(x)=ex-a.若a≤0，则f′(x)>0，f(x)单调递增，其图象与x轴至多有一个交点，不合题意，所以a>0.

点评运用对数平均不等式求解省去了构造增量函数不等式的证明过程，因此解法显得居高临下.该解法的关键是必须把前期的准备工作做好，公式中的a、b分别代表什么，是否都为正数？前期工作做得好才能灵活运用对数不等式.练习4 (2017年苏州一模第20题)已知函数f(x)=(lnx-k-1)x，若x1

2017-03-18)