一道课本上不等式问题的十种证明方法

河北省唐山市丰润区任各庄镇中学 (邮编：064012)

一道课本上不等式问题的十种证明方法

河北省唐山市丰润区任各庄镇中学周来友(邮编：064012)

不等式问题是历年高考中的一个热点问题，其证明方法灵活多样，综合性很强，是高中数学教学中的一个难点.本文以一道不等式的多种证明方法为例，浅谈在不等式证明中经常用到的数学思想和数学方法.

类比转化;数形结合;方程和函数

不等式是研究数学的重要工具，是数学思想和方法的载体，能比较全面地考查学生综合运用数学知识和数学方法解决实际问题的能力，历来都是各类考试的一个热点问题，其证明方法体现了很多数学思想和方法.下面，笔者以一道课本不等式问题的证明为例，提醒大家在复习阶段，注意研究经典问题，真正做到提高复习效率.

本题选自2007年1月第2版的普通高中课程标准实验教科书《数学》选修4-5人教A版不等式选讲第一章第10页习题1.1第11题.

证法1 (用平均不等式)

因为a+b+c=1，所以1=(a+b+c)2

=a2+b2+c2+2ab+2ac+2bc，

又因为a2+b2≥2ab，b2+c2≥2bc，a2+c2≥2ac，所以1≤3(a2+b2+c2)，

证法2 (用柯西不等式)

由柯西不等式可得

证法3 (用配偶不等式)

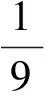
构造以下不等式：

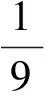
三式相加得，

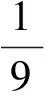
证法4 (构造向量不等式)

而3(a2+b2+c2)=(12+12+12)(a2+b2+c2)，据此构造向量m=(1,1,1)，n=(a,b,c)，

已知a、b、c≥0，

证法5 (用配方法)

因为a+b+c=1，所以c=1-a-b，

所以a2+b2+c2=a2+b2+(1-a-b)2

=2a2+2(b-1)a+2b2-2b+1

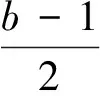
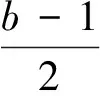
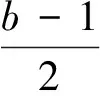
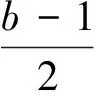
已知a、b、c≥0，

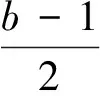
证法6 (构造平方和)

证法7 (构造概率模型)

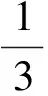
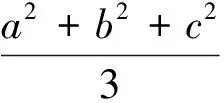
因为Dξ≥0，所以Dξ=Eξ2-(Eξ)2≥0，

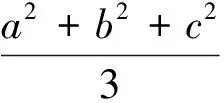
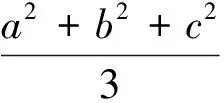
由Dξ=0可知，上式当a=b=c

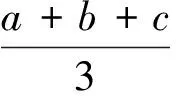
证法8 (构造三角函数)

因为a+b+c=1，所以a+b=1-c，

=1-c.

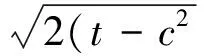
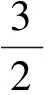
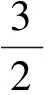
已知a、b、,c≥0，

证法9 (构造二次函数)

以a为主元构造二次函数，设f(a)=a2+b2+c2，因为a+b+c=1，所以c=1-a-b，从而f(a)=a2+b2+(1-a-b)2，

整理得f(a)=2a2+2(b-1)a+2b2-2b+1.

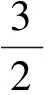
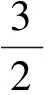
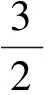
已知a、b、c≥0，

c=1-a-b

证法10 (构造方程组)

整理得3c2-2c+1-2t≥0.

已知a、b、c≥0，

以上证明过程和方法，用到了消元、配方、构造、函数、方程、化归、转化、数形结合等技巧，这些都是最重要的数学思想和方法.由此我们看出，一题多解有利于培养发散思维和综合运用多种数学思想和方法解决实际问题的能力，希望大家在今后的复习中，注意深入挖掘那些典型问题，通过一题多解把基础知识和解题技巧串联起来，以达到研究经典以一当十，解析一题复习一片的目的.

1 人民教育出版社，课程教材研究所，中国数学课程教材研究开发中心.普通高中课程标准实验教科书：数学,选修4-5,A版,不等式选讲[M].北京：人民教育出版社，2008.11-11

2http:∥xue163.com/19990/13691/483607438.html

2017-03-25)