多晶硅薄膜电学输运理论的研究进展
邓幼俊,艾斌
(1. 中山大学物理学院,广东 广州 510006;2. 广东省光伏技术重点实验室,广东 广州 510006;3. 中山大学材料科学与工程学院,广东 广州 510006)
多晶硅薄膜电学输运理论的研究进展
邓幼俊1,2,艾斌2,3
(1. 中山大学物理学院,广东 广州 510006;2. 广东省光伏技术重点实验室,广东 广州 510006;3. 中山大学材料科学与工程学院,广东 广州 510006)
多晶硅薄膜已广泛应用于平板显示、微机电系统和集成电路等领域,在太阳电池和平板系统领域也有着巨大的应用前景。由于多晶硅薄膜存在晶界,晶界内的晶体缺陷和悬挂键会向带隙中引入界面态,界面态一方面会束缚载流子并形成势垒阻碍载流子的传输,另一方面会作为有效复合中心加重载流子的复合,因此,多晶硅薄膜上制备的器件的性能要低于与之对应的单晶硅薄膜器件的性能。为了从理论上阐明暗场和光照条件下多晶硅薄膜的电学性质,人们已发展了各种理论模型。此外,为了确定晶界界面态在带隙中的分布,人们已发展出分析法和计算机模拟两种方法。本文将简要概述人们在多晶硅薄膜电学输运理论和晶界界面态分布确定方法等方面的主要研究进展,以期对从事多晶硅薄膜或多晶半导体输运性质研究的科研工作者有所参考和启发。
多晶硅薄膜;晶界;界面态;电学性质
由于可以在多种衬底上大面积制备器件级多晶硅薄膜,而且能够制成高质量n沟道或p沟道薄膜晶体管(TFTs),所以多晶硅薄膜在平板显示(FPDs)、微机电系统(MEMS)和集成电路(ICs)等领域已获得了广泛的应用[1-5],此外,多晶硅薄膜在太阳电池和平板系统(SOP: system on panel)等领域也有着巨大的应用前景[6-8]。由于晶界的影响,多晶硅薄膜展现出与单晶硅薄膜截然不同的电学性质,且多晶硅薄膜的电学性能往往直接决定了器件的性能。因此,无论是从基础研究还是应用研究的角度来看,多晶硅薄膜电学性质的研究都非常重要的。
事实上,人们已对多晶硅薄膜的电学性质进行了大量的实验和理论研究[9-12]。但因多晶硅薄膜结构复杂多样、与制备条件及后处理工艺密切相关,所以不同的研究者会给出截然不同甚至是相互矛盾的报道。以晶界界面态在带隙中的分布为例,虽然大部分学者认为界面态密度在带隙中央附近有一个极大值[13-19],但也有部分学者认为界面态密度在带隙中央附近取最小值[20-24]。就多晶硅薄膜电学性质的理论研究而言,尽管人们提出了各种理论模型来解释实验现象,譬如:晶界陷阱理论[13-16]、复合型晶界势垒模型[25]、电子态密度分布模型[20]和电势波动模型[26]等。但是,只有晶界陷阱理论和复合型晶界势垒模型可以对多晶硅薄膜的电学输运性质给出定量解释。其中,晶界陷阱理论的适用范围最广、认可度最高[17,27-28],而其他理论模型往往是针对特定的多晶硅薄膜的电学性质而提出的定性解释。本文将只介绍主流的多晶硅薄膜电学输运性质的理论研究,并根据其重要性的不同做不同篇幅的介绍。首先,介绍以晶界陷阱理论和复合型晶界势垒模型为代表的暗场条件下的多晶硅薄膜的电学输运理论,然后介绍以Card模型和Joshi模型为代表的光照条件下多晶硅薄膜的电学输运理论和晶界界面态在带隙中分布的确定方法,最后是关于电学输运理论的展望。
1 暗场条件下多晶硅薄膜的电学输运理论
1.1 Seto的晶界陷阱理论
多晶硅薄膜是由大量结构和性质截然不同的晶粒和晶界组成的混合相材料。虽然晶粒可以近似看作是单晶体,但晶界的结构却非常复杂。根据结晶质量的不同,晶界的厚度可以从几个nm变到几十个nm,内部结构按有序度从高到低可以依次是共格晶界、小角晶界、大角晶界、混合型晶界、随机晶界、受限制的微晶硅层和受限制的非晶硅层等[10]。由于不同位置的晶界在结构和电学性质上可能会发生显著变化,所以从理论上准确求解实际的多晶硅薄膜的电学输运过程几乎是不可能的,事实上也是不必要的。
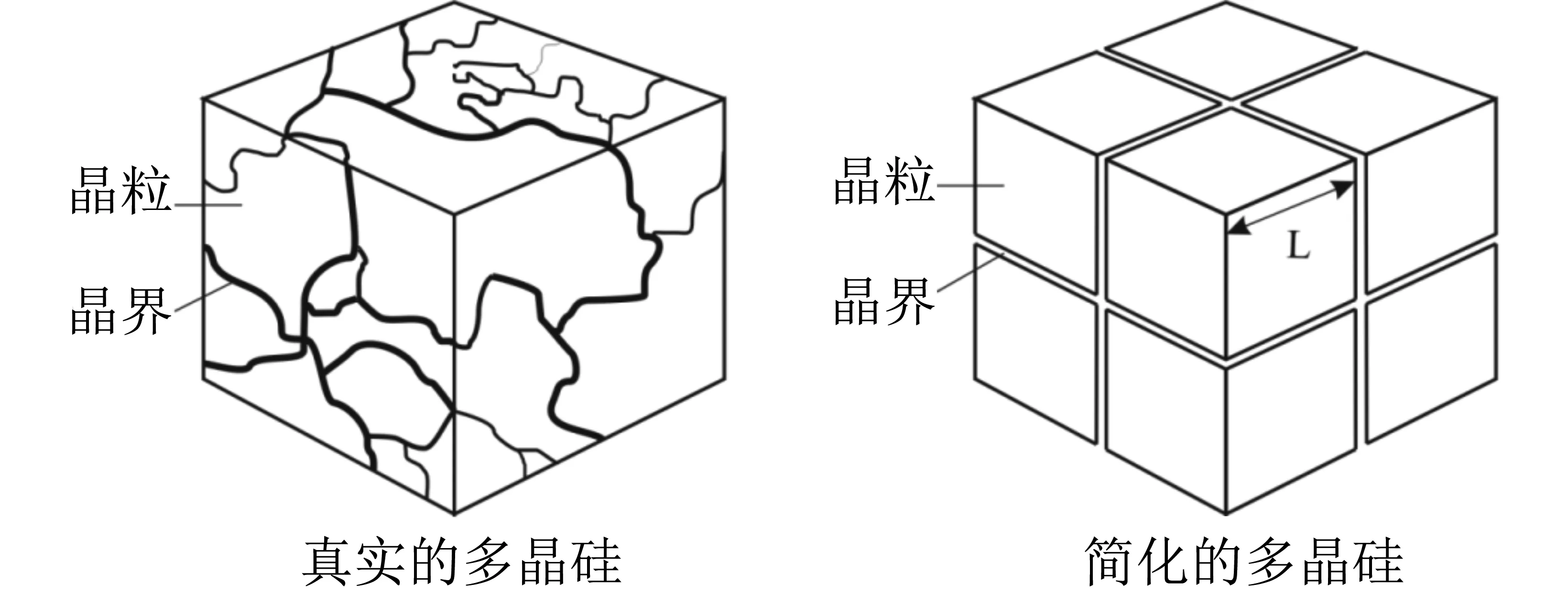
图1 多晶硅实际结构和理论简化结构的示意图[29]Fig.1 The schematic diagram of practical structure and theoretically simplified structure of polycrystalline silicon[29]
1975年Seto[13]提出了第1个能够定量解释多晶硅薄膜电学性质的理论——单能级晶界陷阱模型。为了建立该理论,Seto首先对真实的多晶硅做了如下简化:① 晶粒尺寸相同,晶界厚度可以忽略,如图1所示;② 晶界界面态在带隙中具有单一的陷阱能级和态密度;③ 掺杂原子在晶粒内全部电离等。前2个假设实际上是分别忽略了晶粒间的差别和晶界间的差别,对晶界界面态在带隙中的分布采用了最简单的δ函数分布;第3个假设则是忽略了杂质分凝的影响。之后,Seto建立了如下的物理图像来描述晶界对多晶硅电学性质的影响:晶界内大量的晶体缺陷和悬挂键会在带隙中引入高密度的深能级陷阱态;晶界陷阱态一方面会俘获经过晶界的载流子,从而减少参与导电的载流子数量;另一方面,晶界陷阱态一旦俘获了载流子后就荷电,形成晶界势垒,阻止载流子从一个晶粒向另一个晶粒的传输,从而减小载流子的迁移率,如图2所示。最后,Seto在以上假设的基础上,考虑电子在一维方向上输运,在Poisson方程、电中性条件和热电子发射理论等的基础上推导出计算晶界势垒高度、平均载流子浓度和电导率等物理量的数学公式。
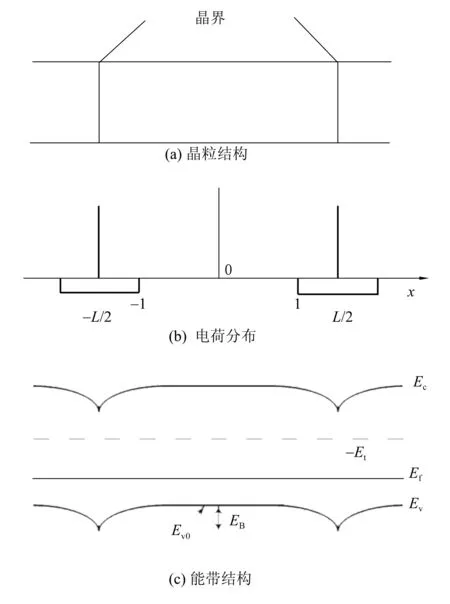
图2 p型多晶硅晶粒结构、电荷分布和能带结构的示意图[13] Fig.2 The schematic diagram of crystal structure, charge distribution and energy band structure of p-type polycrystalline silicon crystallites [13]
尽管Seto提出的单能级晶界陷阱模型可以定量解释绝大多数多晶硅薄膜的电学性质,但是该模型也存在一些限制,主要表现在:① Seto只考虑了晶界区的电阻而忽略了晶粒区电阻,该假设对于重掺杂的大晶粒多晶硅薄膜不适用;② Seto假设晶界陷阱态在带隙中的分布为δ函数分布,然而研究表明如果考虑晶界陷阱态在带隙中呈一定的分布,那么理论结果可以与实验结果符合得更好;③ Seto假设晶界界面态未被填满时晶粒是耗尽的,该假设使得Seto的单能级晶界陷阱理论只适用于晶粒尺寸较小的多晶硅薄膜。针对以上不足,Baccarani等[14]考虑了晶粒部分耗尽时还应存在晶界陷阱态未被填满的情况对Seto的理论作了修正。Lu等[15]则进一步引入了晶粒耗尽区厚度这个参数,在Baccarani工作的基础上对Seto的理论作了修正和完善,使得晶界陷阱理论能够适用于不同晶粒尺寸的多晶硅薄膜。在此之后,Seager等[16]则总结出晶界陷阱态在带隙中分布的一般特征。此外,Seager对单个晶界电阻率随温度变化规律的研究从实验上直接证明了晶界陷阱理论的正确性。至此,一个能够定量解释多晶硅薄膜电学性质的晶界陷阱理论建立起来了。
1.2 Mandurah的复合型晶界势垒模型
除了Seto等人建立和完善的晶界陷阱理论以外,还有一个物理模型的影响较大,那就是Mandurah等[25]于1981年提出的复合型晶界势垒模型。复合型晶界势垒模型是为了解释某些特殊条件下生长的多晶硅薄膜(结晶质量较差、晶界区存在明显的非晶成分,且掺杂较重、存在明显的杂质分凝现象)的电学性质而提出来的。为了使理论模型符合实际的情况,Mandurah作了如下假设:① 晶界的厚度不能忽略,引入晶界区厚度这个物理量;② 晶界区失序度介于单晶硅和非晶硅之间,根据非晶硅1.5~1.6 eV的光学带隙,晶界区的带隙宽度应大于单晶硅的带隙,因此,宽带隙的晶界区与两个相邻的窄带隙单晶硅晶粒相连会形成晶界势垒;③ 杂质会在晶界处分凝,且不会电离,因此晶界区可被看作是具有一定厚度的本征宽带隙半导体材料。根据以上假设,Mandurah给出了复合型晶界势垒模型,如图3所示。该势垒由宽带隙晶界材料(譬如微晶硅或非晶硅)与晶体硅连接形成的晶界势垒和由晶界陷阱作用在晶界区两边形成的耗尽区势垒组成。在研究载流子越过耗尽区势垒时,考虑热电子发射机制;研究载流子穿过晶界势垒时,考虑量子隧穿。2002年,孟凡英等[12]修正了这个模型,她认为:从晶界中心到晶粒有一个微晶硅过渡层,在计算量子隧穿电流时应该用高斯型晶界势垒代替矩形晶界势垒。最近人们的观点似乎对复合型晶界势垒模型不太有利。为了将小晶粒多晶硅薄膜与微晶硅薄膜区别开来,Altermatt等[10]提出:当晶粒之间的非晶硅层厚度小于0.5 nm时,可认为材料从微晶硅薄膜过渡到多晶硅薄膜。按照这种观点,多晶硅的Mandurah复合型晶界势垒模型实际上又回到了Seto的晶界势垒模型,因为计算表明几个晶格厚度的势垒对于载流子的量子隧穿几乎是透明的[9]。
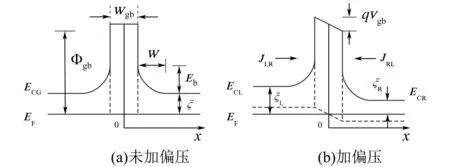
图3 Mandurah的复合型晶界势垒模型的示意图[25]Fig.3 The schematic diagram of Mandurah’s grain boundary barrier model for n-type polycrystalline silicon film without a bias voltage (a) and with a bias voltage (b)[25]
2 光照条件下多晶硅薄膜的电学输运理论
2.1 Card的模型
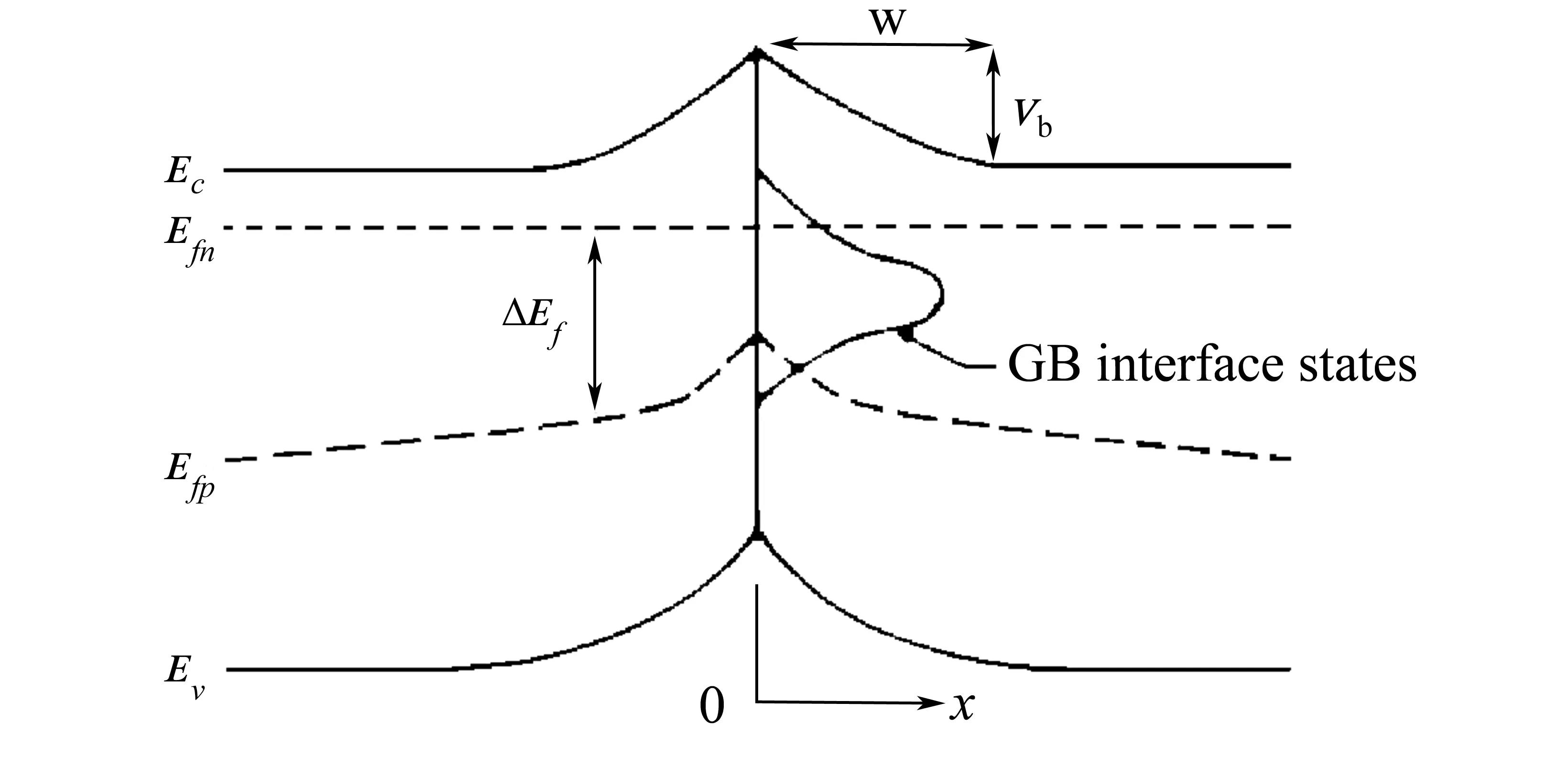
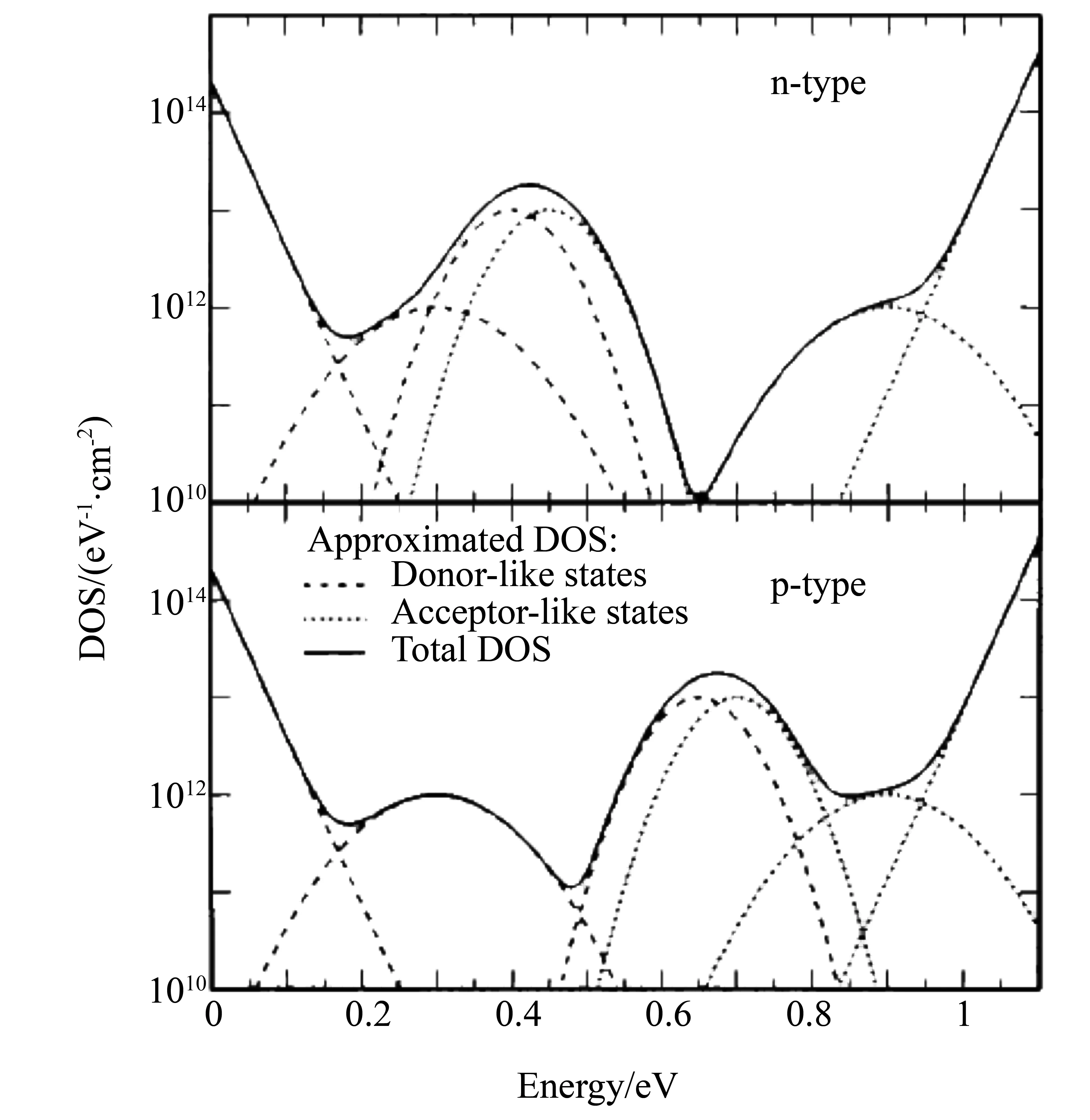
就光伏应用而言,人们更关心的是多晶硅薄膜在光照条件下的电学性质。1977年Card等[30]提出了第一个能够定量解释光照下多晶硅薄膜电学性质的理论模型。他以n型多晶硅薄膜为例,给出了光照对晶界势垒以及载流子分布影响的物理图像:未受光照前,晶界处会形成一个多子(电子)势垒。当材料受到光照,材料内部出现了过剩的少数载流子(空穴),结果一些晶界界面态因捕获空穴变为空态,晶界荷电量减小,势垒高度降低,这反过来又减少了对空穴的俘获,直到达到新的动态平衡,如图4所示。为了简化,Card等作了如下假设:① 晶界界面态在带隙中连续分布,且不随能量变化;② 晶界界面态对电子和空穴的俘获截面相等;③ 晶界处的电子浓度等于空穴浓度;④ 复合电流很小,不会造成耗尽区内(-W 图4 Card 给出的n型多晶硅晶界附近区域在暗场和光照下的能带图[30]Fig.4 The energy band diagram near a grain boundary of n-type polycrystalline silicon in the dark and under illumination given by Card [30] 2.2 Joshi的模型 针对已有的光照下多晶硅晶界复合和电导模型的不足,1990年,Joshi等[31-32]以n型多晶硅为例提出了一个比较全面的、描述光照条件下多晶硅薄膜电学性质的模型。为了使新的模型不受前人理想化假设局限性的限制,他们做了如下假设:① 多晶硅由平均晶粒尺寸为d的立方体形单晶粒构成;② 晶界耗尽区宽度远小于晶粒尺寸d;③ 在样品各处光生电子和光生空穴的产生率是一样的;④ 多子的准费米能级处处平坦,但少子的准费米能级可以随位置而改变,如图5所示;⑤ 每个晶界界面态具有两个不同的载流子俘获截面,分别对应于电中性界面态对载流子的俘获截面(σN)和带电界面态作为库仑吸引中心对载流子的俘获截面(σC)。若用σp和σn分别表示界面态对空穴和电子的俘获截面,对于n型多晶硅则有σp=σC和σn=σN;⑥ 假设只有一种界面态对复合起作用,对于n型多晶硅只包含类受主型界面态,对于p型多晶硅只包含类施主型晶界态;⑦ 假设晶界界面态在带隙中呈高斯型分布(见图5),且高斯型分布的3个特征参数与掺杂浓度和晶粒大小无关;⑧ 与晶界复合电流密度相比,空间电荷区的复合和产生电流密度可以忽略。在以上假设的基础上,他们利用S-R-H间接复合等理论推导出光照下晶界势垒高度、晶界耗尽区边缘有效复合速度、晶界复合电流密度、耗尽区边缘及体区的少数载流子浓度及多晶硅电阻率等一系列物理量的数学表达式。此外,他们还利用这些公式研究了不同光照水平(产生率)、不同晶粒尺寸、不同少数载流子体扩散长度与晶界势垒高度、晶界复合电流密度、晶界耗尽区边缘有效复合速度、费米能级分裂距离、电阻率等的关系。由此不难看出,与Card模型相比,Joshi模型是一个相当全面的描述光照下晶界复合和电导的理论。 图5 Joshi 给出的光照下n型多晶硅晶界附近区域的能带图[31]Fig.5 The energy band diagram near a grain boundary of n-type polycrystalline silicon under illumination given by Joshi [31] 多晶硅薄膜的电学性质主要是由晶界势垒决定的。要想正确预测晶界势垒的高度,就需要准确了解晶界界面态密度随能量的分布,目前,人们已发展出两种确定晶界界面态分布的方法,即分析法和计算机模拟法。 3.1Yamamoto给出的分析法[18-19] 通过计算多晶硅电阻率激活能(Ea)与掺杂浓度(N)的关系,并用它来拟合实测的Ea-N曲线,以确定晶界陷阱态分布函数在理论上似乎是可行的,但实际操作起来很困难。为了解决这个问题,Yamamoto等提出了利用实测的Ea-N曲线来确定晶界陷阱态分布函数Nt(E)的分析方法。下面将以p型多晶硅为例简要介绍该方法的梗概并给出相关公式。根据晶界陷阱理论,p型多晶硅薄膜的电阻率可表示为: (1) 式中,m*表示空穴有效质量,k表示玻尔兹曼常数,T表示温度,q表示电子电量,p表示晶粒中的自由空穴浓度,L表示晶粒尺寸,Eb表示晶界势垒高度。如果掺杂浓度的增加(ΔN)引起了晶界陷阱态捕获的单位面积上空穴数量的增加(或者晶界势垒区单位面积上带电量的增加ΔQt)和晶界费米能级的上升(ΔEfb),那么晶界费米能级Efb处的晶界陷阱态密度可表示为: (2) 根据掺杂浓度大小的不同,分两种情况给出Efb处的晶界陷阱态密度Nt(Efb)的具体表达式。 当掺杂浓度较轻使得晶粒完全耗尽时,能带图为: Efb-Ev=Ea (3) 式中,Ev表示晶界区的价带顶。由(2)式和(3)式可得: (4) 当掺杂浓度较重使得晶粒部分耗尽时,假设系统具有统一的费米能级,且电中性区的载流子浓度等于掺杂浓度,能带图为: Efb-Ev=Eb+Ev0-Efg= (5) 式中,Ev0表示电中性区的价带顶,Efg表示电中性区的费米能级,Eg表示带隙宽度,ni表示本征载流子浓度。相应地,此时Efb处的晶界陷阱态密度Nt(Efb)可表示为: (6) 式中,ε表示多晶硅的绝对介电常数。使用(4)和(6)式计算晶界陷阱态密度Nt(E)时,必须知道晶粒从完全耗尽向部分耗尽转变的临界掺杂浓度N*。然而,在确定出Nt(E)之前无法得到N*的准确值。因此,通常使用(4)和(6)式对所有能级计算晶界陷阱态密度Nt(E)。当晶粒完全耗尽,由(4)式计算的晶界陷阱态密度Nt(E)有效;当晶粒部分耗尽时,由(6)式计算的晶界陷阱态密度Nt(E)有效。至此,可根据实测的Ea-N曲线来确定晶界陷阱态分布函数Nt(E)。具体的求解过程如下:首先利用Efb-Ev的值确定Ea值;其次根据实测的Ea-N曲线得到与Ea值对应的掺杂浓度N和曲线斜率ΔEa/ΔN的值;最后,利用(4)和(6)式计算出对应于Efb-Ev的晶界陷阱态密度Nt(E)。 3.2 计算机模拟法[10] 针对高能晶界包含了几个nm厚度的受限制非晶硅层,Altermatt于2002年从缺陷池模型出发并结合前人对晶界界面态分布的研究来推断受限制非晶硅层悬挂键(dangling bonds)和浮动键(floating bonds)引起的晶界界面态的分布;然后利用半导体器件三维模拟软件Dessis使用离散的方法和数值迭代过程求解反映晶界势垒区静电特性(Poisson方程)、复合特性(SRH间接复合理论)和载流子传输特性(热电子发射理论)的非线性半导体方程组,以实现对暗场和光照条件下p型和n型多晶硅电学性质实验结果的拟合;通过对实验结果拟合,成功得到了晶界界面态的分布,如图6所示,p型和n型多晶硅晶界界面态都是由类施主态D+/0和类受主态D0/-组成的,而且D+/0和D0/-都是由一个指数带尾、一个与指数带尾末端接近的浅隙态高斯分布和一个在带隙中央附近的深隙态高斯分布组成的,所不同的是类受主态D0/-位于带隙上半部分,而类施主态D+/0位于带隙下半部分。作者宣称利用这种界面态分布曲线和三维器件模拟软件Dessis比前人更精确地拟合了已报道的多晶硅电学性质实验结果。 图6 由缺陷池模型和计算机模拟法得到的晶界界面态密度分布曲线[10](类受主态D0/- 位于带隙上半部分,类施主态D+/0 位于带隙下半部分)Fig.6 The distribution curves of grain boundary interface state density obtained by the defect-pool model combining simulation with acceptor-like states D0/- in the upper half of the bandgap and donor-like states D+/0 in the lower half of the gap 综上所述,尽管人们已经对多晶硅薄膜的电学性质进行了大量的研究,但由于多晶硅薄膜两相结构的复杂性和多样性、以及多晶硅薄膜的电学性质与制备条件和后处理工艺条件密切相关等因素,至今人们在一些问题上仍存在争议。譬如:晶界界面态的特性是怎样的?晶界界面态在带隙中是如何分布的?为了解释实验现象,人们赋予了晶界界面态不同的性质和分布。其中,Seager等[16]认为界面态是单电子态,态密度呈δ函数(或类似函数)分布,且峰值在带隙中央附近;而Joshi等[31-32]认为N型多晶硅薄膜只有类受主态D0/-起作用,而P型多晶硅薄膜只有类施主态D+/0起作用,且两者在带隙中都呈高斯分布。Altermatt等[10]利用缺陷池模型和数值模拟方法对前人的多晶硅电学性质实验结果进行拟合,得到了一种更加复杂的界面态分布曲线。结果表明:p型和n型多晶硅晶界界面态都是由类施主态D+/0和类受主态D0/-组成的,而且D+/0和D0/-都是由一个指数带尾、一个与指数带尾末端接近的高斯分布和一个在带隙中央附近的高斯分布组成的,所不同的是D0/-位于带隙上半部分,而D+/0位于带隙下半部分。Altermatt的这项工作引起了相关学者的极大关注,因为截止目前还没有一个物理模型能够解释已报道的p型和n型多晶硅在暗场和光照条件下电学性质的实验结果。而,Altermatt声称采用缺陷池模型所推断出的晶界界面态分布函数、单一的模拟模型和三维器件模拟软件Dessis能够比前人更精确地拟合已报道的p型和n型多晶硅在暗场和光照条件下电学性质的实验结果。Altermatt的工作给了我们两点启示:其一是可以通过对实验数据的拟合来推测晶界界面态的分布函数;其二是正确的晶界界面态分布函数对解释多晶硅电学性质至关重要。事实上,这一点不难理解,因为多晶硅的电学性质主要是由晶界势垒决定的,而要想正确预测晶界势垒的高度,就需要准确知道晶界界面态的本质、性质和态密度随能量的分布。 我们认为要准确预测多晶硅薄膜的电学性质,除了要有能正确反映多晶硅电学输运物理机制的晶界势垒模型以外,还需要准确知道晶界界面态的特性和在带隙中的分布,而采用能够正确反映晶界势垒形成的物理模型结合数值模拟方法,对已报道的p型和n型多晶硅在暗场和光照条件下电学性质的实验结果进行拟合,以确定晶界界面态的性质和分布仍将是未来多晶硅薄膜电学性质理论研究的重要方向。我们有理由相信,随着研究的深入,多晶硅薄膜晶界界面态的特性和分布最终将得到全面揭示。 通过文献回顾不难发现:人们普遍认可和接受的观点是晶界中键长和键角的畸变会在带隙中引入靠近带边的带尾态,因为它们既不能储存大量的电荷,也不能对复合产生显著的影响,因此它们对多晶硅薄膜电学性质的影响是次要的。而晶界中的悬挂键会在带隙中引入靠近带隙中央的深能级界面态,它们既可以充当俘获载流子的陷阱中心,又能够起到有效复合中心的作用,因此它们对多晶硅薄膜的电学性质起到决定性的影响,哪怕晶界中悬挂键的含量较少。晶界对多晶硅薄膜电学性质的影响主要表现在两方面:一方面晶界界面态会俘获流经晶界的载流子形成势垒阻碍载流子从一个晶粒向另一个晶粒的传输,另一方面,晶界界面态会充当有效的载流子复合中心加剧光照下多晶硅薄膜中载流子的复合。在多晶硅薄膜电学性质的定量解释方面,Seto的晶界陷阱理论适用于绝大多数多晶硅薄膜,而Mandurah的复合型晶界势垒模型适用于Seto理论不适用的极个别情况,比如:晶化不完全、掺杂较重、存在明显杂质分凝的多晶硅薄膜。Card模型是第一个将S-R-H间界复合理论引入来解释光照条件下多晶硅电学性质的理论模型。与Card模型相比,Joshi摒弃了以往较多的不合理假设,提出了一个比较全面的、描述光照条件下多晶硅电学性质的理论模型。在确定晶界界面态在带隙中的分布方面,Yamamoto给出的分析法简单直接有效,但得到的晶界界面态在带隙中的分布不够精细。而采用数值模拟与晶界势垒模型相结合的方法能够比较准确地确定晶界界面态在带隙中的分布,但缺点是求解过程艰难繁琐复杂、耗时较长。 [1] SAMESHIMA T. Laser crystallization for large-area electronics [J]. Appl Phys A, 2009, 96(1): 137-144. [2] PARK J H, SEOK K H, KIM H Y, et al. Compressive stressed P-channel polycrystalline-silicon thin-film transistors for high field-effect mobility[J]. IEEE Electron Device Lett, 2015, 36(8): 793-795. [3] MAHFOZ-KOTB H, SALAUN A C, MOHAMMED-BRAHIM T, et al. Polycrystalline silicon thin films for MEMS applications[J]. Thin Solid Films, 2003, 427(1/2): 422-426. [4] NAITO T, KONNO N, TOKUNAGA T, et al. Doping characteristics of polycrystalline silicon deposited by chemical transport at atmospheric pressure and its application to MEMS sensor[J]. IEEE Sensors J, 2013, 13(8): 2899-2905. [5] CHEN Yuanning, BU Haowen, BUTLER S W, et al. Manufacturing benefits of disilane as a precursor for polycrystalline silicon films for the advanced CMOS gate electrode[J]. IEEE Trans on Semiconductor Manufacturing, 2005, 18(1): 42-48. [6] ZHANG Meng, ZHOU Wei, CHEN Rongsheng, et al. A simple method to grow thermal SiO2interlayer for high-performance SPC poly-Si TFTs using Al2O3gate dielectric[J]. IEEE Electron Device Lett, 2014, 35(5): 548-550. [7] DORE J, ONG D, VARLAMOV S, et al. Progress in laser-crystallized thin-film polycrystalline silicon solar cells:intermediate layers, light trapping, and metallization[J]. IEEE J of Photovoltaics, 2014, 4(1): 33-39. [8] BECKER C, AMKREUTZ D, SONTHEIMER T. Polycrystalline silicon thin-film solar cells: status and perspectives[J]. Solar Energy Mat & Solar Cells, 2013, 119(12): 112-123. [9] SEAGER C H. Grain boundaries in polycrystalline silicon[J]. Annual Rev of Mat Sci, 1985, 15(8): 271-302. [10] ALTERMATT P P, HEISER G. Predicted electronic properties of polycrystalline silicon from three-dimensional device modeling combined with defect-pool model[J]. J of Appl Phys, 2002, 92(5): 2561-2574. [11] KIMURA M, INOUE S, SHIMODA T, et al. Current paths over grain boundaries in polycrystalline silicon films[J]. Japanese J of Appl Phys, 2001, 40: 97-99. [12] MENG Fanying, CUI Rongqiang. Novel model of electrical conduction property at grain boundary in polysilicon[J]. Japanese J of Appl Phys, 2002, 41: 185-189. [13] SETO J Y W. The electrical properties of polycrystalline silicon films[J]. J of Appl Phys, 1975, 46(12): 5247-5254. [14] BACCARANI G, RICCO B, SPADINI G. Transport properties of polycrystalline silicon films[J]. J of Appl Phys, 1978, 49(11): 5565-5570. [15] LU N C C, GERZBERG L, MEINDL J D. A quantitative model of the effect of grain size on the resisitivity of polycrystalline silicon resistors[J]. IEEE Electron Device Lett, 1980, 1(3): 38-41. [16] SEAGER C H, CASTNER T G. Zero-bias resistance of grain boundaries in neutron-transmutation-doped polycrystalline silicon[J]. J of Appl Phys, 1978, 49(7): 3879-3889. [17] AI Bin, SHEN Hui, LIANG Zongcun, et al. Electrical properties of B-doped polycrystalline silicon thin films prepared by rapid thermal chemical vapour deposition[J]. Thin Solid Films, 2006, 497(1/2): 157-162. [18] YAMAMOTO I, KUWANO H, SAITO Y. Energy distribution of trapping states at grain boundaries in polycrystalline silicon[J]. J of Appl Phys, 1992, 71(7): 3350-3355. [19] YAMAMOTO I, KUWANO H. Determination of the energy distribution of grain boundary traps in polycrystalline silicon films[J]. Japanese J of Appl Phys, 1992, 31: 1381-1382. [20] HIROSE M, TANIGUCHI M, OSAKA Y. Electronic properties of chemically deposited polycrystalline silicon[J]. J of Appl Phys, 1979, 50(1): 377-382. [21] HIRAE S, HIROSE M, OSAKA Y. Energy distribution of trapping states in polycrystalline silicon[J]. J of Appl Phys, 1980, 51(2): 1043-1047. [22] WENER J, PEISL M. Exponential band tails in polycrystalline semiconductor films[J]. Phys Rev B Condensed Matter, 1985, 31(10): 6881-6883. [23] FORTUNATO G, MIGLIORATO P. Determination of gap state density in polycrystalline silicon by field-effect conductance[J]. Appl Phys Lett, 1986, 49(16): 1025-1027. [24] GRAAFF H C D, HUYBERS M. Grain boundary states and the characteristics of lateral polysilicon diodes[J]. Solid State Electronics, 1982, 25(1): 67-71. [25] MANDURAH M M, SARASWAT K C, KAMINS T I. A model for conduction in polycrystalline silicon: theory[J]. IEEE Trans on Electron Devices, 1981, 28(10): 1163-1171. [26] ADA-HANIFI M, SICART J, DUSSEAU J M, et al. A model of conduction in polycrystalline silicon films[J]. J of Appl Phys, 1987, 62(5): 1869-1876. [27] MICHALAS L, KOUTSOURELI M, PAPAIOANNOU G J, et al. Hydrogen passivation on sequential lateral solidified poly-Si TFTs[J]. Microelectronic Eng, 2012, 90(2) : 72-75. [28] GROZDANIC D, MILAT O, RAKVIN B, et al. Grain boundary defects in RTCVD polycrystalline silicon for solar cells[J]. Vacuum, 2001, 61(2/4): 257-262. [29] 王阳元,卡明斯,赵宝瑛, 等. 多晶硅薄膜及其在集成电路中的应用[M]. 2版. 北京:科学出版社, 2001:1-30. [30] CARD H C, YANG E S. Electronic processes at grain boundaries in polycrystalline semiconductors under optical illumination[J]. IEEE Trans on Electron Devices, 1977, 24(4): 397-402. [31] JOSHI D P, BHATT D P. Theory of grain boundary recombination and carrier transport in polycrystalline silicon under optical illumination[J]. IEEE Trans on Electron Devices, 1990, 37(1): 237-249. [32] JOSHI D P, BHATT D P. Grain boundary barrier heights and recombination velocities in polysilicon under optical illumination[J]. Solar Energy Mat, 1991, 22(2/3): 137-159. Researchprogressoncarriertransporttheoryofpolycrystallinesiliconthinfilms DENGYoujun1,2,AIBin2,3 (1.SchoolofPhysics,SunYat-senUniversity,Guangzhou510006,China;2.GuangdongProvinvialKeyLaboratoryofPhotovoltaicTechnology,Guangzhou510006,China;3.SchoolofMaterialsScienceandEngineering,SunYat-senUniversity,Guangzhou510006,China) Polycrystalline silicon (poly-Si) thin films have been widely used in flat panel displays, MEMS(micro-electro-mechanical system) and integrated circuits, and also have great application prospects in other areas such as solar cells and SOP (system on panel). Since there exist grain boundaries (GBs) in poly-Si thin films, the crystal defects and dangling bonds in GB regions would introduce interface states in the band gap. On the one hand, the interface states would trap carriers thus creating barriers against carrier transportation, on the other hand, they could act as effective recombination centers to strengthen the recombination. Therefore, the performance of devices fabricated on poly-Si thin films is generally worse than that on single-crystal silicon thin films. To give a theoretical explanation on the electrical properties of poly-Si thin films under the dark and illumination conditions, various theoretical models have been proposed. In addition, two kinds of ways including analytical method and computer simulation have been developed to determine the energy distribution of interface states in the band gap. This article will briefly review the major research progress in electrical transport theory of poly-Si films and methods for determining the distribution of the interface states, so that researchers engaging in investigation on transport properties of poly-Si thin films or polycrystalline semiconductors could get some reference and inspiration. polycrystalline silicon thin film; grain boundaries; interface states; electrical properties 10.13471/j.cnki.acta.snus.2017.04.007 2016-12-21 基金项目:广东省科技计划项目(2011A032304001, 2013B010405011) 邓幼俊(1965年生),男;研究方向:太阳能利用;E-mail:dengyj@mail.sysu.edu.cn O472+ A 0529-6579(2017)04-0038-08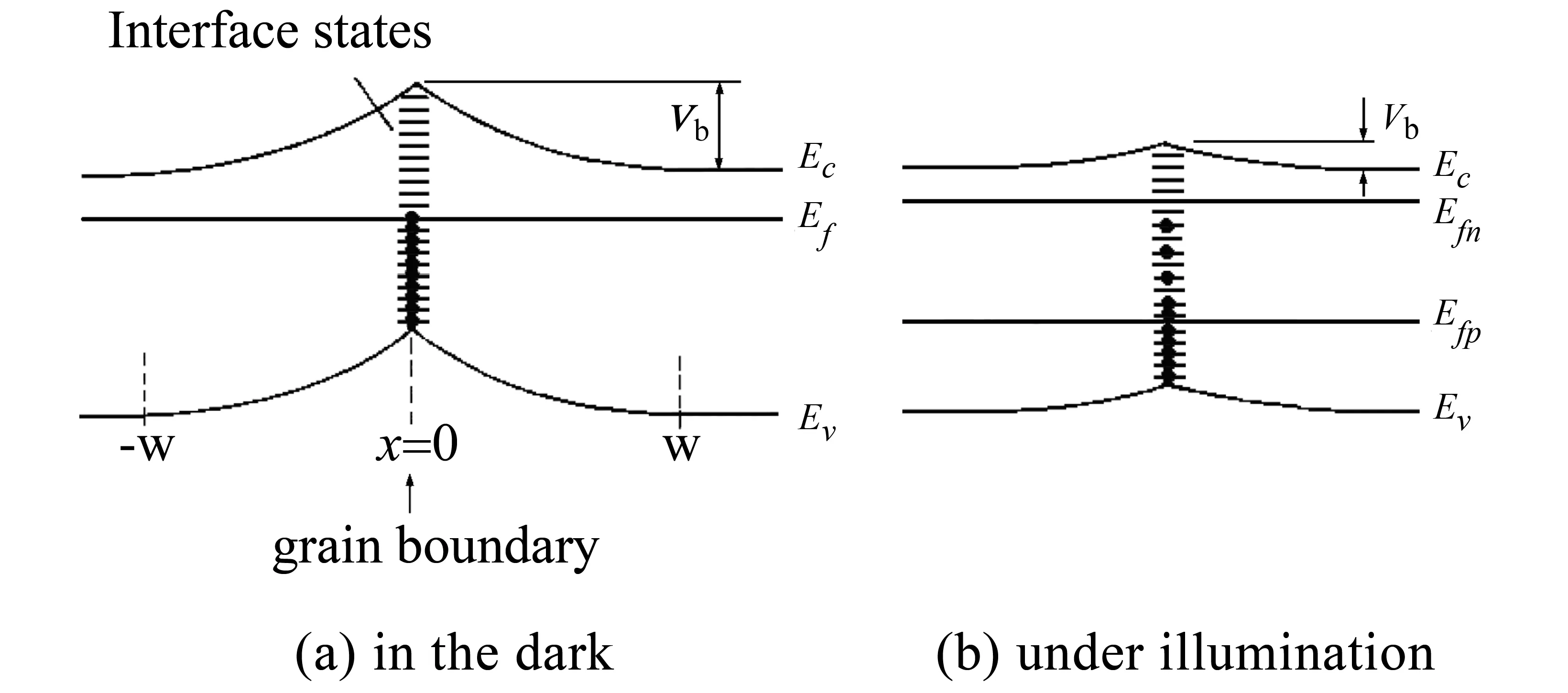
3 确定晶界界面态在带隙中分布的方法
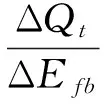
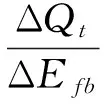
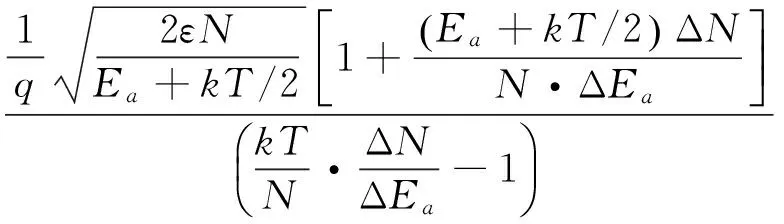
4 展 望
5 结 论

