基于残余力向量法和树种算法的结构损伤识别二步法
赵一霖,刘济科,吕中荣,丁政豪
(中山大学工学院,广东 广州 510006)
基于残余力向量法和树种算法的结构损伤识别二步法
赵一霖,刘济科,吕中荣,丁政豪
(中山大学工学院,广东 广州 510006)
基于二步法对结构进行了损伤识别。首先,通过改进残余力向量定位方法对结构单元进行排查、找出疑似单元;然后基于频域参数建立目标函数,并利用元启发式树种算法(Tree-seed algorithm)对于结构损伤进行反演。为了改善算法的优化能力,引入了两种局部搜索模式,并采用具有自适应性的判断参数来判定使用何种模式进行局部开发。最后,采用梁和悬臂板作为算例进行损伤识别,并得到了识别结果。结果表明:在仅知道有限频域参数的情况下,提出的算法能够有效地识别损伤参数,优于其他进化算法并且对测量噪声不敏感。
树种算法;残余力;板;梁结构;频域参数
结构损伤识别一直是土木工程领域的热点分支之一。结构损伤的及时发现可以避免重大事故的发生[1]。在许多相关研究中,学者将结构裂纹模型等价为单元刚度矩阵中杨氏模量的减少、可扭转弹簧、一种完全开口的裂纹模型等等[2-4]。结构损伤识别问题往往被归结为优化问题,即通过定义一个关于损伤结构的目标函数,然后利用各种优化方法来实现结构参数的损伤检测[5]。经典的优化方法往往需要好的初始值,借助梯度和导数等信息,这极大地限制了这类方法的应用[6]。元启发式算法可以弥补经典优化方法的不足,在众多的元启发式算法中,树种算法因为结构简单,寻优能力较GA,PSO等算法更强[7],进而受到了广泛关注。本文利用改进的树种算法来实现损伤程度的反演和识别,并引入了两种更好的搜索模式和自适应判断参数,使得迭代的初期算法侧重于全局搜索、迭代后期算法则更侧重于于局部搜索,以实现两种搜索能力(局部搜索和全局搜索)的平衡。同时,本文假定损伤模型为单元质量和刚度的线性折损,通过频率残差和模态确保准则建立了损伤识别的目标函数,结合改进后的算法对该目标函数进行求解以获得损伤参数的识别。结果表明:本文提出的方法相较于GA算法,灵敏度算法而言,收敛速度更快,求解精度更高,鲁棒性更好。
1 改进残余力向量定位法
在不考虑结构阻尼的前提下,完好结构的运动方程对应的特征方程为:
其中,M和K分别为结构的质量矩阵和刚度矩阵,λj和φj分别为结构的第j阶特征值和特征向量。当某种结构发生损伤时,其物理参数将会发生改变。为不失一般性,假设只有刚度参数发生改变,则损伤后的结构所对应的特征方程是:
Kdφdj=λdjMφdj
(2)

将等式(3)代入等式(2),得:
等式(4)的右边为残余力向量(residualforcevector,RFV)[8],即第j阶损伤结构残余力fj,其值的计算公式为:
传统残余力向量法中往往利用某一阶的模态求得的残余力,这可能会漏掉一些损伤单元。为了获得更加全面准确的损伤位置,利用由前p阶模态求得的改进残余力向量来进行损伤定位,即
其中,每一维变量通过公式(7)计算,即:
其中p为所选模态参数的阶数。
1.1 目标函数
基于频率残差和模态确保准则建立的目标函数,如下所示:
从上式可以发现,当识别的损伤越接近于真实损伤的时候,该目标函数越接近于0。所以,完全可以借助元启发式算法来解决损伤程度的反演问题。
1.2 改进的树种算法
树种算法是一种新型的元启发式算法,它通过模拟大树的繁殖方式来实现最优值的寻找。首先,每一棵树(可行解)会随机地产生若干种子,每一颗种子可由两种迭代方式产生新解,其中一种方式侧重于全局搜索,另一种侧重于局部搜索。选择何种方式迭代由搜索趋势常数ST决定。然后,若干种子各自寻优,用其中最优秀的一个可行解来替换原始解以实现进化。所以,与一般的群智能算法(如人工蜂群算法[9]和萤火虫算法[10])相比,该算法的局部搜索模式更为剧烈和精细,具备更好的全局寻优能力。文献[7] 详细介绍了树种算法的具体操作,本文重点介绍算法的改进和优化。
1.2.1 全局寻优能力的改善 在标准算法中,树种的全局搜索模式借鉴了人工蜂群算法[9]中引领蜂的局部寻优模式:
其中,Si,j是第i颗树繁殖地第i颗种子中第j个变量的变异结果,Tr,j是种群中的另一棵树的第j个变量,α则是一个位于[-1,1]之间的随机数。因为,全局搜索是为了避免算法在迭代的时候陷入局部最优,所以应该尽可能地利用种群中其他个体的信息。利用差分进化算法中的DE/rand/2/bin变异机制对待优化变量的每一维变量进行变异则更为合理。文献[9]已经明确指出:差分进化机制相较于其他引领蜂搜索机制有更强的全局寻优能力,所以用公式(11)来产生新解:
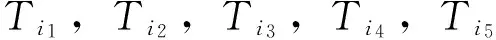
1.2.2 局部寻优能力的改善 在原始算法中,树种的局部搜索方式是通过围绕着此次迭代中最好的那一棵树周边进行随机搜索来实现的,如公式(12)所示:
其中,Bj是迭代中适应度最好的那一棵树的第j个变量,α是位于[-1,1]之间的随机数, 围绕着最好的可行解周边进行探索是非常有利于算法收敛的。为了更好地实现这个目的,改进算法中采用以下方式探索:
1.2.3 搜索趋势常数ST的改进 在原始算法中,判断参数ST一直是常数。本文采用搜索趋势函数来决定树种的迭代模式,搜索趋势函数如下所示:
式中,cycle表示当前的迭代步数,Maxcycle则表示最大迭代步数。引入这样的非线性函数,可以使得迭代初期侧重于树种的全局搜索而后期侧重于局部搜索,可以保证算法的收敛。
2 数值模拟
2.1 简支梁算例
为了便于和其它群智能算法进行对比,选取文献[12]中的简支梁作为算例。该结构总共有20个单元,杨氏模量E=70GPa,密度ρ=2.70×103kPa,泊松比为0.33,如图1所示。损伤工况为1号单元损伤12.5%的杨氏模量,9号单元损伤50%的杨氏模量,算法参数设置为种群大小40、最大迭代次数30,采用前三阶的频率和模态进行计算。首先,利用残余力向量定位法,算出各个自由度上的数值如图2所示。从中可以推断:1, 2, 8, 9和10号单元为疑似损伤单元。然后,将他们带入改进的树种算法中进行计算。图3为基于两种算法的目标函数的迭代曲线,可以明显地发现改进算法得到的目标函数值更接近0,这预示着相应地识别结果更为优秀。如图4所示,在没有噪声的情况下,改进的树种算法可以精确地识别出损伤, 而标准算法得到的最大误差发生在1号单元上为0.876%。当频率添加1%、模态添加10%的噪声之后,利用本文算法,1号单元的误差为0.086%, 9号单元的误差为0.229%,优于Kang等利用免疫粒子群算法得到的结果(1号单元误差为0.276%, 9号单元误差为1.292%), 也优于文献[12]中利用遗传算法,粒子群算法和差分进化算法得到的识别结果。在误判方面,Kang等[12]得到了两处误判,而本文的改进算法没有误判,并且只要30次的迭代就可以得到较为理想的识别结果,远小于文献[12]里面预设的200次最大迭代次数。
2.2 悬臂板算例
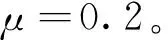
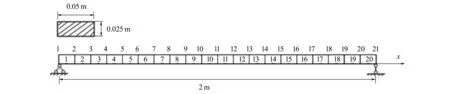
图1 简支梁以及它的横截面[12]
Fig.1 Simply supported beam and its cross section[12]
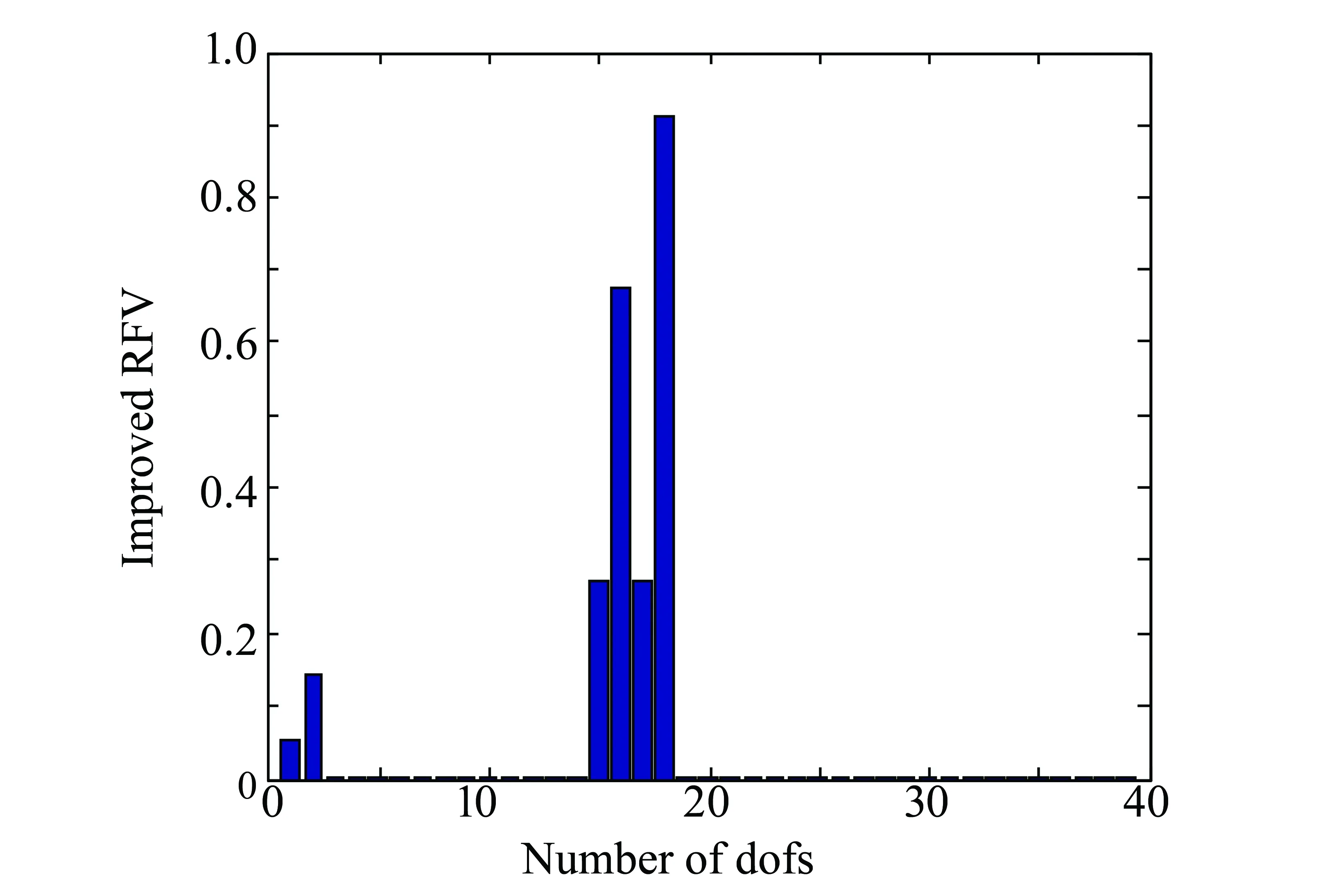
图2 工况1各个自由度的残余力Fig.2 The residual force of each freedom under the first condition
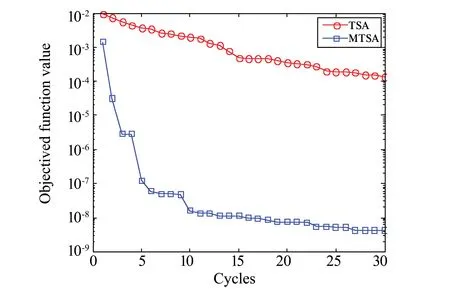
图3 基于两种算法的目标函数进化曲线Fig.3 The evolution curve of objective function based on two algorithms
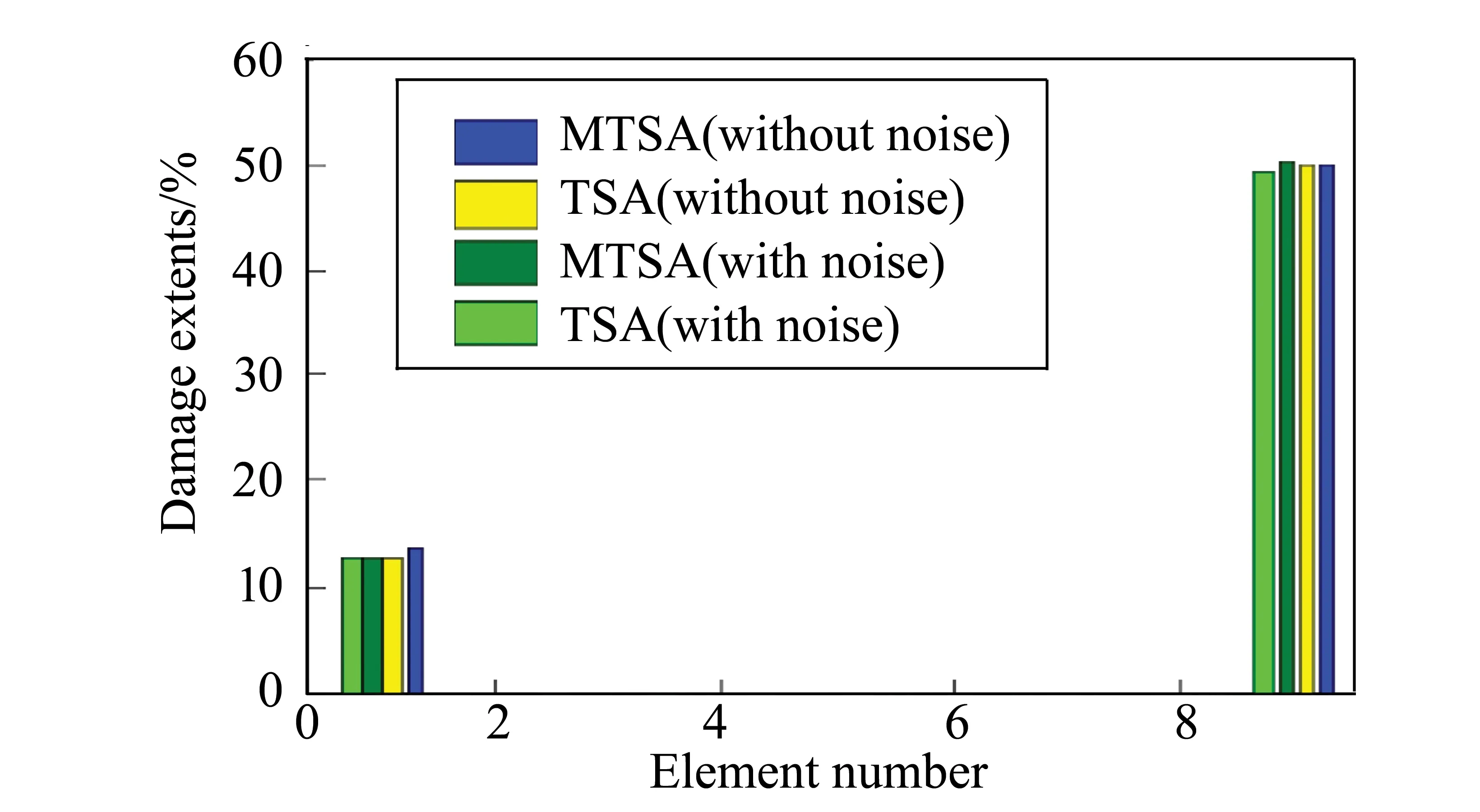
图4 工况1的识别结果Fig.4 The identification results under the first condition
所示。可以发现:1-6号自由度,13-18号自由度,28-33号自由度, 37-42号自由度存在着明显的峰值。这意味着1-7号, 10-11号,13-15号单元为疑似损伤单元。以它们为优化变量带入算法,得到最后的识别结果,如图7所示。
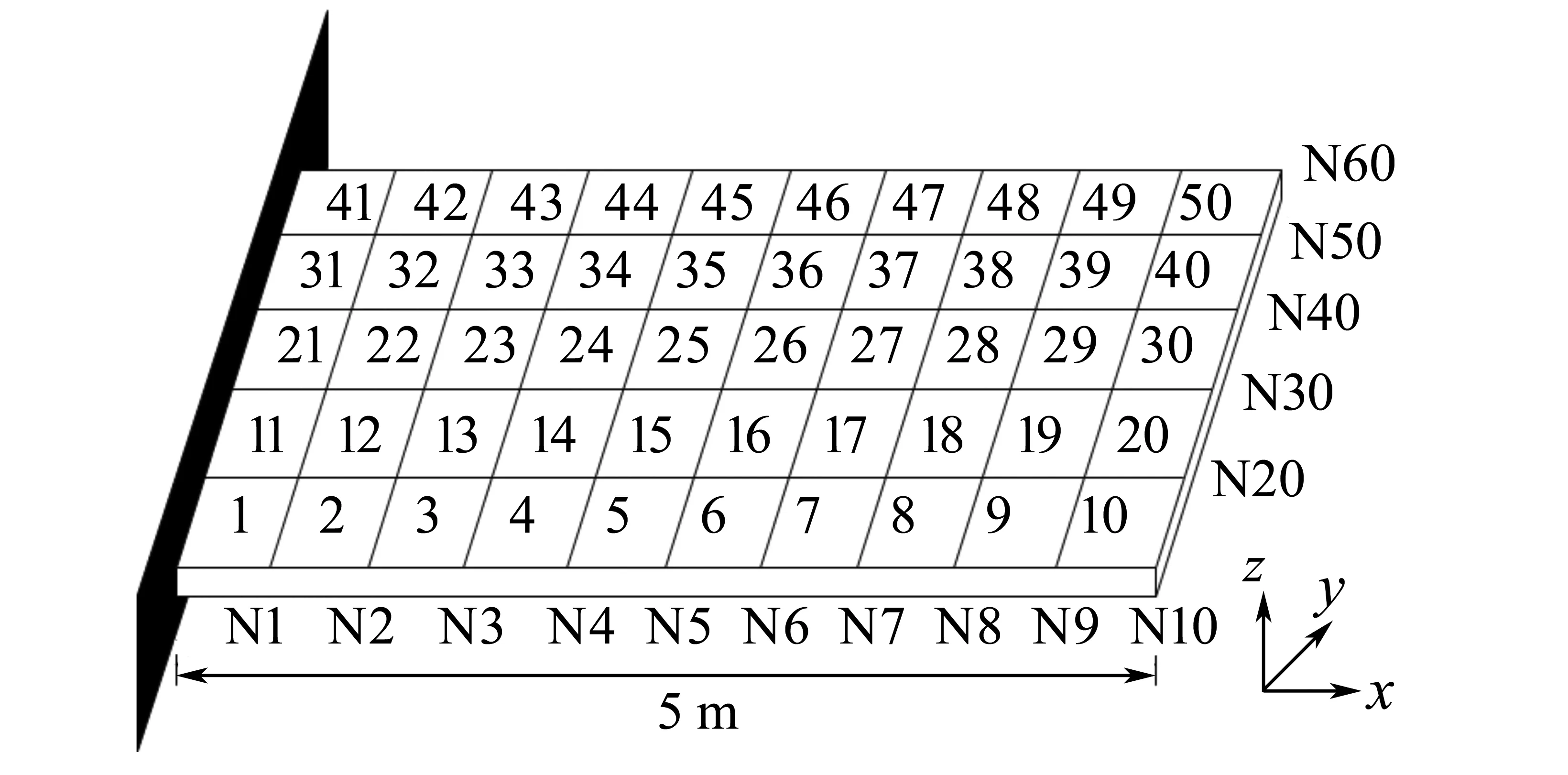
图5 悬臂板模型Fig.5 Cantilever plate model
在没有噪声干扰的情况下,本文提出的方法能够精确识别出损伤,而基于TSA算法得到的最大误差发生在14号单元(0.601%)。当添加同等级的噪声之后,基于改进算法得到的最大误差发生在14号单元上,但也仅为0.367%。为了测试本文算法的有效性,引入混沌蜂群算法[13]做对比, 识别结果如图8所示。在加入同等级的噪声之后,基于混沌蜂群算法得到的最大误差发生在5号单元,为1.245%。 因此,可以明显发现发现借助于本文的方法得到的识别结果更具有竞争力。
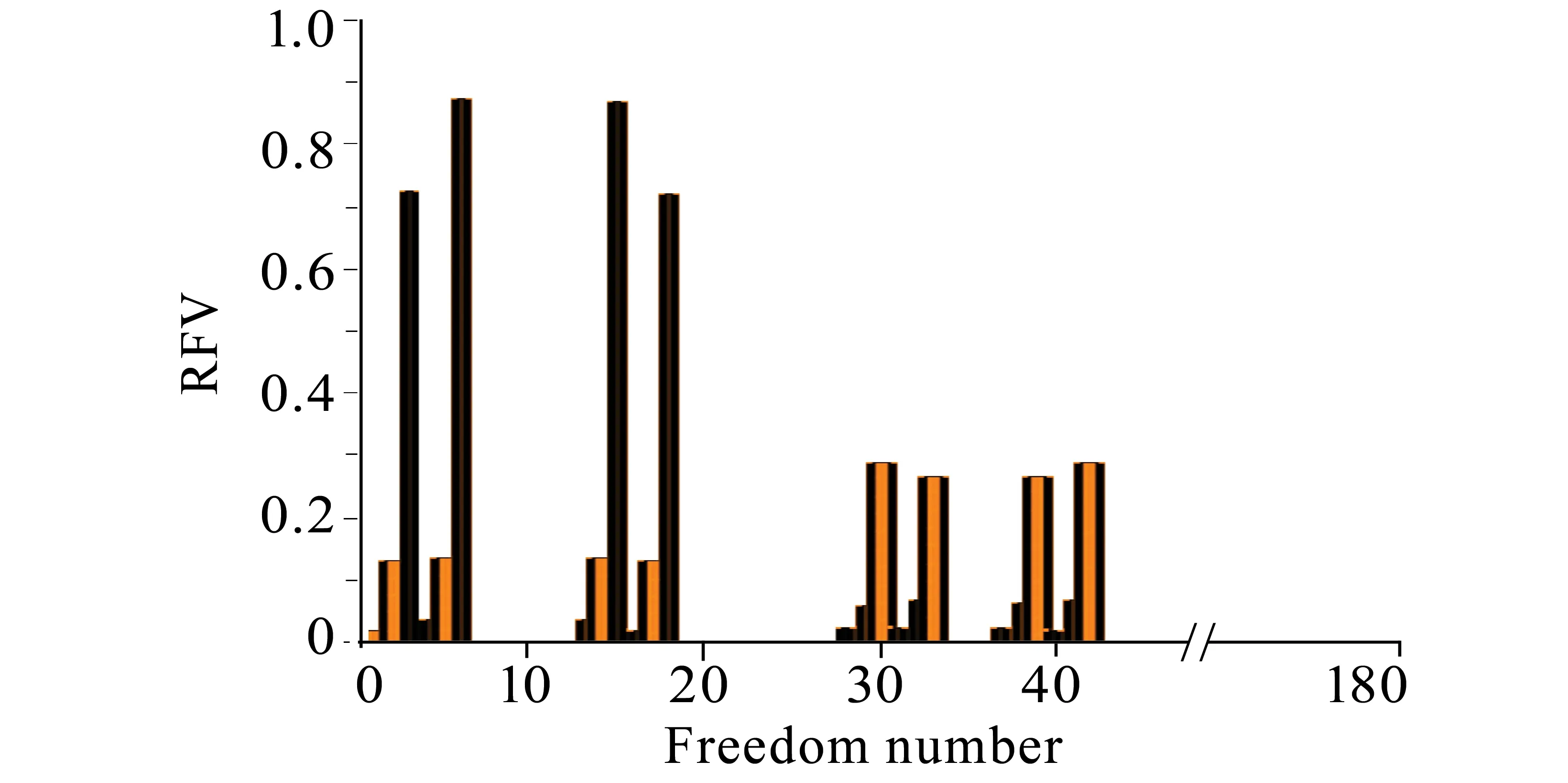
图6 工况2各个自由度的残余力Fig.6 The residual force of each freedom under the second condition

图7 工况2的识别结果(未标出来的单元意味着无损)Fig.7 The identification results under the second condition(no marked unit means nondestructive)
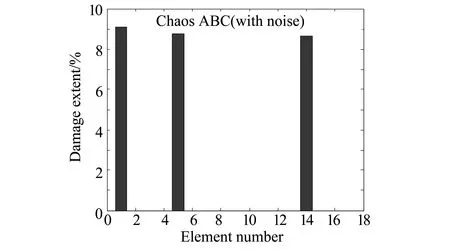
图8 工况2的识别结果(未标出来的单元意味着无损)Fig.8 The identification results under the second condition(no marked unit means nondestructive)
3 结 论
本文采用残余力向量和树种算法的二步法对梁结构和悬臂板进行了损伤识别。研究通过初次定位排查了大量无损单元,为第二步的定量识别奠定了基础。同时,对树种算法进行了改进,引入了两个搜索能力更强的搜索模式;改进算法采用搜索趋势函数做判断参数,使得全局搜索能力更强,搜索速度更快。在梁结构算例中,与其他群智能算法的对比表明:本文的算法具有更好的搜索精度和鲁棒性;在板结构算例中,与混沌蜂群算法的对比表明:本文的算法更有有效性。虽然只用了梁和悬臂板结构作为算例,但此方法并非局限于这类结构。对于更复杂的结构,只要合理地构建目标函数,本文的方法都具有借鉴意义。
[1] 刘济科,汤凯. 基于振动特性的损伤识别方法的研究进展[J].中山大学学报(自然科学版),2004,43(6):57-61.LIUJike,TANGKai.Advancesofvibration-baseddamageidentificationmethods[J].ActaScientiarumNaturaliumUniversitatisSunyatseni, 2004, 43(6): 57-61.
[2]LUZR,LAWSS.Featuresofdynamicresponsesensitivityanditsapplicationindamagedetection[J].JournalofSoundandVibration, 2007, 303: 305-329.
[3]CHENGSM,SWAMIDASASJ,WUXJ,etal.Vibrationresponseofabeamwithabreathingcrack[J].JournalofSoundandVibration, 1999, 225: 201-208.
[4]SINHAJK,FRISWELLMI,EDWARDSS.Simplifiedmodelsforthelocationofcracksinbeamstructuresusingmeasuredvibrationdata[J].JournalofSoundandVibration, 2002, 251: 13-38.
[5]SHENMHH,TAYLORJE.Identificationproblemforvibratingcrackedbeams[J].JournalofSoundandVibration, 1991, 150: 457-484.
[6]GOKDAGH.Acrackidentificationapproachforbeam-likestructuresundermovingvehicleusingparticleswarmoptimization[J].MaterialsTesting, 2014, 55(2):114-120.
[7]KIRANMS.TSA:tree-seedalgorithmforcontinuousoptimization[J].ExpertSystemswithApplications, 2015, 42: 6686-6698.
[8]RICLESJM,KOSMATKAJB.Damagedetectioninelasticstructuresusingvibrationresidualforcesandweightedsensitivity[J].AIAA, 1991, 30(9): 2310-2316.
[9]LIXiangtao.Parameterestimationforchaoticsystemsbyhybriddifferentialevolutionalgorithmandartificialbeecolonyalgorithm[J].NonlinearDyn, 2014, 77:61-71.
[10]YANGXS.Fireflyalgorithm,stochastictestfunctionsanddesignoptimization[J].InternationalJournalofBio-InspiredComputation, 2010, 2(2):78-84.
[11]GAOW,LIUS,HUANGL.Aglobalbestartificialbeecolonyalgorithmforglobaloptimization[J].JournalofComputationalandAppliedMathematics, 2012, 236: 2741-2753.
[12]KANGF,LIJJ,XUQ.Damagedetectionbasedonimprovedparticleswarmoptimizationusingvibrationdata[J].AppliedSoftComputing, 2012, 12(8): 2329-2335.
[13] 丁政豪,徐法杰,刘济科,等.基于混沌人工蜂群算法的结构损伤识别[J].中山大学学报(自然科学版),2015,54(5):39-42.DINGZhenghao,XUHaojie,LIUJike,etal.DamageidentificationbasedonchaoticABCalgorithm[J].ActaScientiarumNaturaliumUniversitatisSunyatseni, 2015, 54(5): 39-42.
Structural damage identification based on residual vectors and Tree-seed algorithm
ZHAO Yilin,LIU Jike,LYU Zhongrong,DING Zhenghao
(School of Engineering, Sun Yat-sen University, Guangzhou 510006,China)
A two-step method is proposed to solve structural damage identification problem. First, the improved residual vector is used to locate the general damage range, and then used Tree-seed algorithm (TSA) is used to identify damage extents based on objective function related to damage structures. TSA is a heuristic algorithm with simple structure and easy to implement. In order to make it more powerful, two kinds of search modes and a self-adaptive judge factor are utilized to realize algorithm’s search. A beam and a plate are employed as numerical simulations. Studies show that the present techniques can produce more accurate damage identification results, comparing with other algorithms, even with a little noise contaminated measurements.
TSA; residual vector; beam; plate; frequency domain.
10.13471/j.cnki.acta.snus.2017.04.008
2017-02-13 基金项目:国家自然科学基金(1117233);广东省自然科学基金(2015A030313126);广东省科技计划项目(2014A020218004, 2016A020223006)
赵一霖 (1993年生),女;研究方向:结构健康监测;E-mail:2274004920@qq.com
吕中荣(1975年生),男;研究方向:结构健康监测;E-mail: lvzhr@mail.sysu.edu.cn
O39
A
0529-6579(2017)04-0046-05

