基于切换控制的低频半主动悬架动态性能分析

伍俊,熊建栋,陈广义,郭静

(1. 佛山科技学院自动化学院, 广东 佛山 528000;2.河南师范大学数学与信息科学学院, 河南 新乡 453007)

基于切换控制的低频半主动悬架动态性能分析

伍俊1,熊建栋2,陈广义1,郭静1

(1. 佛山科技学院自动化学院, 广东 佛山 528000;2.河南师范大学数学与信息科学学院, 河南 新乡 453007)

针对车辆半主动悬架系统建立了切换系统模型，并利用输出反馈切换控制策略对该系统进行了控制率设计。为了分析控制率的控制效果，基于有理函数滤波白噪声生成法模拟路面不平度，并利用MATLAB/Simulink软件对悬架系统因路面不平度所产生的振动进行了仿真。结果表明：基于切换控制的低频半主动悬架与被动悬架相比，车身加速度降低了22%，悬架动挠度降低了36%，轮胎动载荷降低了13%。因此，基于切换控制的低频半主动悬架控制策略可以明显改善车辆的动态性能，提高车辆的乘坐舒适性及操纵稳定性。

半主动悬架；切换系统；路面不平度；动态性能

随着科技的不断发展，人们对汽车的性能要求越来越高。而悬架系统的技术状况直接影响汽车的舒适性、安全性、操作稳定性等，因此也得到了生产企业、研究人员等的关注和重视[1]。由于悬架系统自身复杂的多自由度随机振动特性，要对其进行精确的描述和分析比较困难。在悬架系统的基础选择合适的控制策略，以保障控制效果就更加充满挑战。传统的研究方法是将悬架视为线性系统，采用线性理论进行控制策略设计和振动分析[2-5]。然而，汽车悬架是典型的非线性系统。随着控制理论的发展， 近年来各国学者陆续提出了基于神经网络理论、模糊控制理论、滑模变结构控制理论等的控制策略[6-8]。上述控制方案有各自的前提条件，与实际的工况有不同程度的差异，在实车应用时也各有利弊。因此，有必要对汽车半主动悬架控制策略做进一步探索和研究。可以预见，对半主动悬架系统而言，综合考虑模型的准确性、控制方案的稳健和可实现性是其发展的方向。切换系统已成为控制界研究的热点。究其原因，除了切换系统本身所蕴含的多模态所引起的复杂性，还因实际应用中很多系统都可以用切换系统来描述[9-10]。事实上，半主动悬架系统属于典型的切换系统，可以利用切换理论建立更精确的数学模型，并对控制策略进行设计及分析[11-12]。文献[12]对1/4车辆悬架系统进行了分析研究，提出了基于线性切换系统理论的建模及控制方案设计，不仅降低了磁流变阻器的切换频率，同时也可保证系统的稳定性，但该文献未对此方案下的控制效果进行分析。本文基于新的参变量及控制要求重新设计了控制器，并验证了该控制策略下系统的稳定性。进一步地，、采用滤波白噪声生成法来模拟路面不平度，并利用 MATLAB/Simulink软件对汽车随机振动时域响应进行了研究。

1 基于切换理论的车辆半主动悬架系统建模

图1所示为1/4车体的半主动悬架系统的动力学模型。图中，M是悬架簧载质量；m是悬架非簧载质量，包括轮胎、车轮、悬架连接杆等的质量；zt为车轮质心的垂向位移；z为车身质心的垂向位移；zr为路面不平度激励；kt为轮胎刚度；k为悬架刚度；c为半主动悬架(可变)阻尼系数，满足条件c∈{cmin,cmax}, 其中cmin，cmax为常值。

图1 1/4车体半主动悬架系统的动力学模型Fig.1 Dynamical model of semi-active control for 1/4 suspension system

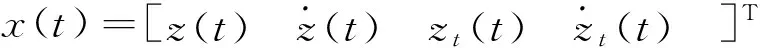
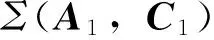
2 低频半主动悬架输出反馈切换控制策略设计

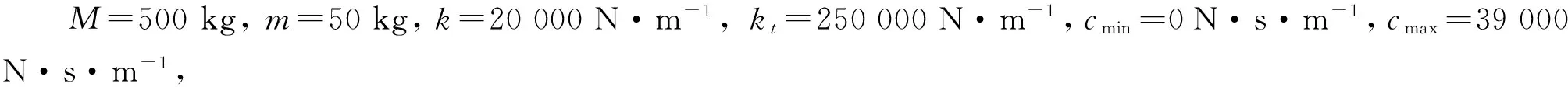
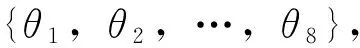
考虑到实际系统状态难以直接测量，对该半主动悬架系统设计观测器。考虑基本切换间隔，可选定每一个子系统Lurberger观测器的增益矩阵为：

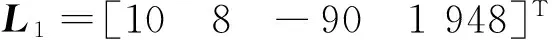
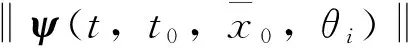
(11)

实际上，上述切换率是由切换路径串接起来的，每一段切换路径执行完毕后，都重新在已给定的切换路径组中选出收敛程度最大的那一条并执行，以此类推即可得该切换率。任意给定初始值，可得半主动悬架系统在该切换率控制下是渐进稳定的。图2显示的是切换控制策略下的系统状态及切换信号。由图可知，系统状态是稳定的，而且切换的频率有保障。

3 振动特性分析及数字仿真

车辆悬架系统的主要目的是保证乘客乘坐的舒适性和安全性。此外，车辆悬架系统还要保证悬架行程控制在允许的限度内，并在载荷变化、加速、制动、转弯时符合车身姿态的要求。综上所述，对于一个给定的悬架系统，可用以下3个基本参数来定量评价悬架系统的性能。首先是车身垂向加速度，由于人体对垂向振动较为敏感，垂直加速度的均方根值与乘客的舒适感觉成线性关系，因此，可计算乘员座椅位置，即车身垂向加速度的均方根值表征乘坐舒适性。其次是悬架弹簧的动挠度。由于悬架限位行程的存在，使得弹簧压缩到最大行程时，将会撞击限位块，影响行驶平顺性及操纵的稳定性，因此动挠度也是必须考虑的一个指标。第三个需要考虑的指标是轮胎动载荷，即轮胎对路面的动载荷，这是由于当动载荷变化较大时，有可能车轮会跳离地面，严重影响车轮操纵的稳定性和安全性。本文对上述3参数进行计算和分析，以评估控制策略的有效性。

3.1 随机激励路面模型

汽车行驶过程中振动产生的主要激励来自于路面的起伏，也就是路面的不平度。 它影响车辆行驶的平顺性、操纵稳定性、零部件疲劳寿命等各个方面。因此，在不平路面激励下的汽车振动响应性能是评估悬架控制策略的常用方法。

基于Matlab强大的计算功能，对低频半主动悬架输出反馈控制下的半主动悬架系统编写M文件，并进行仿真。本文中，作为车辆振动输入的路面不平度由滤波白噪声产生，其时域数学模型为[13]：

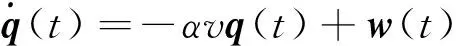
(12)

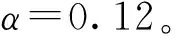
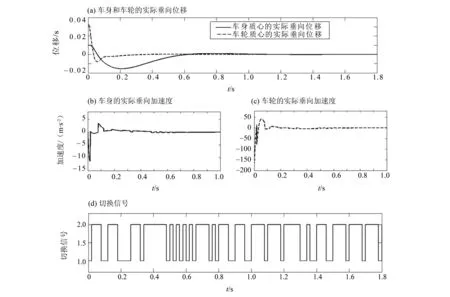
图2 切换控制策略下的系统状态及切换信号图
Fig.2 System status and switching signal under switching control strategy

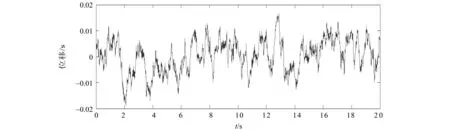
图3 车速为 20 m/s、B 级路面激励的路面不平度时域仿真结果Fig.3 Time domain simulation of pavement routhness on B-class road and for speed of 20 m/s

3.2 低频切换控制策略与被动悬架的仿真结果对比

基于上述路面模型, 在 Matlab/Simulink环境下进行仿真, 结果如图4-5所示。此外，各响应量的均方根值如表1所示。由图表可知，低频切换控制策略极大地降低了悬架动挠度，车身加速度，对轮胎动载荷也有较好改善，即低频切换策略不仅降低了磁流变阻器的切换频率，也证明了系统的稳定性，而且还极大地改善了乘坐舒适性，同时也改善了操纵稳定性。

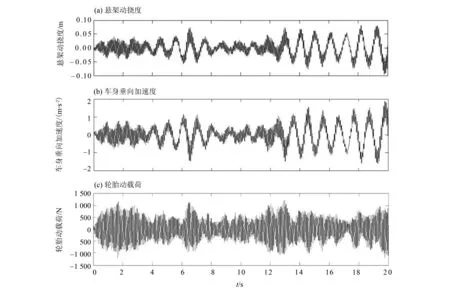
图5 切换低频控制策略下各响应量曲线Fig.5 Response curves under switching control strategy

项目车身垂向加速度/(m·s-2)悬架动挠度/m轮胎动载荷/N被动悬架1.3020.028862.3切换控制1.1280.018750.3降低百分比/%223613

4 结 论

本文基于已有的低频切换控制策略，在新的参变量及控制要求下重新设计了控制器，并验证了该控制策略下系统的稳定性；利用滤波白噪声生成法来模拟路面不平度，通过 MATLAB/Simulink软件对悬架振动进行了分析。数值算例的结果表明：低频切换策略不仅降低了磁流变阻器的切换频率，而且还极大地改善了乘坐舒适性，同时也改善了操纵稳定性，在实际工程中具有较好的应用价值。

[1] 寇发荣，方宗德. 汽车可控悬架系统的研究进展[J]. 汽车工程,2007, 29(5)： 426-432. KOU Fangrong, FANG Zongde. The research trend in controlled suspension system of vehicles[J]. Automotive Engineering,2007, 29(5)：426-432.

[2] 任宏斌, 陈思忠, 冯占宗．基于天棚On-Off控制的磁流变半主动悬架研究[J]. 北京理工大学学报,2014, 34(2): 148-152. REN Hongbin, CHEN Sizong, FENG Zhanzong. The skyhook on-off control of semi-active suspension with magneto-rheological damper[J]. Transactions of Beijing Institute of Technology, 2014, 34(2): 148-152.

[3] 庞辉, 付文强, 刘凯,等. 基于天棚控制的半主动悬架建模及稳定性[J]. 汽车工程, 2015, 37(10):1166-1173. PANG Hui, FU Wenqiang, LIU Kai, et al. Modeling and stability analysis of semi-active suspension with sky-hook control[J]. Automotive Engineering,2015, 37(10):1166-1173.

[4] 岳永恒, 王茂, 赵强. 饱和不确定磁流变阻尼器悬架系统反馈控制器的设计[J].汽车工程,2012, 34(7): 613-617. YUE Yongheng, WANG Mao, ZHAO Qiang. The design of feedback controller for the suspension system with saturated uncertain Magneto-rheological damper[J]. Automotive Engineering,2012, 34(7): 613-617.

[5] SILANI E, SAVARESI S E, BITTANTI S．Acceleration-driven-damper (ADD): an optimal control algorithm for comfort-oriented semi-active suspensions[J]. Journal of Dynamic Systems Measurement & Control, 2005, 127(2): 218-230.

[6] WANG H, SHI X . Semi-active suspension control using the RNN inverse system of MR damper[J]. International Workshop on Intelligent Systems and Applications,2010(5): 85-91．

[7] 严天一，任坤儒，王玉林,等. 车辆半主动悬架系统模糊混合控制策略[J]. 农业机械学报,2012, 43(12):11-15. YANG Tianyi, REN Kunru, WANG Yulin, et al. Fuzzy hybrid control strategy of semi-active suspensions for vehicle[J]. Transactions of the Chinese Society for Agricultural Machinery,2012, 43(12):11-15.

[8] 陈云微，赵强. 车辆半主动座椅悬架滑模变结构控制[J]. 哈尔滨工程大学学报, 2012,33(6): 775-781. CHEN Yunwei, ZHAO Qiang. Sliding mode variable structure control for semi-active seat suspension in vehicles[J]. Journal of Harbin Engineering University,2012, 33(6): 775-781.

[9] SUN Zhendong. Stabilizing switching design for switched linear systems: a state-feedback path-wise switching approach[J]. Automatica, 2009, 45(7):1708-1714.

[10] WU Jun, SUN Zhendong. Observer-driven switching stabilization of switched linear systems[J], Automatica,2013, 49(8): 2556-2560.

[11] GEROMEL J C, COLANERI P, BOLZERN P. Dynamic output feedback control of switched linear systems[J]. IEEE Transactions on Automatic Control,2008, 53(3): 720-733.

[12] 伍俊，熊建栋，林梅金,等. 半主动悬架系统的低频反馈镇定设计[C]//第35届中国控制会议论文集. 2016: 579-583. WU Jun, XIONG Jiandong, LIN Meijin, et al. Low-frequency feedback stabilization design for semi-active suspension system[C]// 35thChinese Control Conference. 2016: 579-583.

[13] 吴志成, 陈思忠, 杨林,等. 基于有理函数的路面不平度时域模型研究[J]. 北京理工大学学报， 2009,29 (9) :795-798. WU Zhicheng, CHEN Sizhong, YANG Lin, et al. Model of road roughness in time domain based on rational function[J]. Transactions of Beijing Institute of Technology, 2009, 29 (9) :795-798.

Performanceevaluationoflow-frequencyoutput-feedbackswitchedcontrolstrategyonsemi-activesuspensionsystem

WUJun1,XIONGJiandong2,CHENGuangyi1,GUOJing1

(1.SchoolofAutomation,FoshanUniversity,Foshan528000,China；2.CollegeofMathematicsandInformationScience,HenanNormalUniversity,Xinxiang453007,China)

According to the actual conditions, a switched system model and a control strategy based on the output feedback switching strategy method are proposed for a semi-active suspension system in this work. On the basis of this, in order to further analyze the control effect of the control strategy, a road roughness is produced based on the rational function filter white noise generation method, then analysis and comparison simulation about the vibration produced by the road roughness are carried out by MATLAB/Simulink. The simulation results show that compared with the passive suspension, the low-frequency semi-active suspension control strategy based on switching control is 22% lower, the suspension deflection is 36% lower, and the tire dynamic load is 13% lower. The results show that the low frequency semi-active suspension control strategy based on switching control can improve the dynamic performance of the vehicle and improve the ride comfort and handling stability of the vehicle.

semi-active suspension; switching system; pavement roughness; dynamic performance

10.13471/j.cnki.acta.snus.2017.04.010

2017-03-21 基金项目：国家自然科学基金(61603093)；广东省科技发展专项 ( 2016AG100311)；广东省自然科学基金(2014A030313619)

伍俊(1985年生)，女；研究方向：切换系统和鲁棒控制；E-mail：susanwuj@163.com

郭静(1985年生)，女；研究方向：无线传感器网络和多智能体协作控制；E-mail：guojing_cc@163.com

U

A

0529-6579(2017)04-0058-06