基于剪切波变换和稀疏表示理论的图像融合方法

常莉红

(宝鸡文理学院数学与信息科学学院, 陕西 宝鸡 721013)

基于剪切波变换和稀疏表示理论的图像融合方法

常莉红

(宝鸡文理学院数学与信息科学学院, 陕西 宝鸡 721013)

为了提高噪声图像的融合效果，基于剪切波变换和稀疏表示理论提出了一种对噪声图像的融合方法。基本思想主要包括4步：①对噪声图像进行剪切波分解，得到各个尺度下的剪切波系数；②利用稀疏表示理论对低频子带的剪切波系数进行融合，而对高频子带的系数选用绝对值最大的原则进行融合；③对融合后的剪切波系数进行硬阈值处理； ④利用剪切波逆变换得到最终的结果。实验结果表明所提方法是有效的。

图像融合；剪切波变换；稀疏表示; 多尺度变换

随着各种成像设备的发展, 多种不同类型的传感器对同一场景的图像获取的信息是不同的。为了使一幅图像包含更丰富的信息，往往将多张图像的信息整合成一幅图像，这就是图像融合技术[1]。它已经被广泛的应用到各种领域中，比如目标探测，医学图像诊断以及军事安全等方面。

图像融合的方法很多，但大体可以总结为两类：一类是基于空间像素的融合方法[2-3],而另一类是基于变换域的方法，其中最为流行的方法有多尺度分析方法如离散小波变换(discrete wavelet transform, DWT)[4]，和曲线波变换 ( curvelet transform,CVT)[5]，剪切波变换(shearlet transform, ST)[6]以及稀疏表示融合方法[7-10]。 像素域融合方法简单但容易引起人工瑕疵，多尺度分析方法虽然有效，但融合规则和分解层数很难确定，而且往往会使得图像的对比度降低，稀疏表示融合方法融合结果过于光滑。目前大多方法只是应用到对干净的融合中，但实际上在图像传输和获取的同时往往受到噪声的污染，因此，对被噪声污染的图像进行融合是有实际意义的，比如稀疏表示方法(sparse representation, SR)[11]和多字典稀疏表示方法(adaptive sparse representation, ASR)[12]。为了克服多尺度方法和稀疏融合理论在融合中带了的问题，本文将这两种方法结合起来提了一种基于剪切波和稀疏表示理论的图像融合方法，不仅解决了多尺度分解降低对比度的问题，而且还解决了稀疏表示理论在融合过程中产生过光滑的作用。

1 剪切波变换结合稀疏表示理论的融合算法

1.1 剪切波变换

剪切波变换是用复合膨胀算子基于仿射变换提出的一种多尺度分析工具，其定义为[13]：

(1)

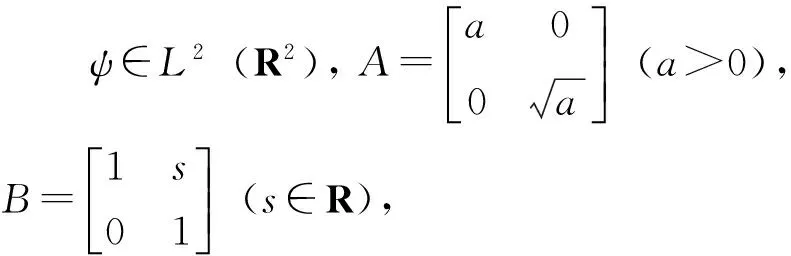
1.2 稀疏表示理论

稀疏表示模型是指用字典中少量的原子的线性组合来描述信号，即设信号x大小为n×n，冗余字典为D，稀疏表示系数是α，则x≈Dα。为了得到稀疏表示系数α通常是求解方程

通常用OMP[14]算法求解。

1.3 融合算法

假设已经配准好的源图像I1,I2被零均值，方差为σ的加性高斯白噪声所污染，即

Ii=ui+ni

其中n∈N(0,σ2) 加性高斯白噪声. 所提算法具体分为5个阶段：

1) 对源图像I1和I2进行剪切波分解得到低通子带{L1,L2}和高通子带{H1,H2}。

2) 对低通子带的剪切波系数进行融合

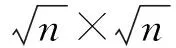
(ii) 对每个i位置的图像块拉成列向量重排得到列向量分别记作vi1和vi2, 并减去均值得到：

(iii) 利用OMP算法计算稀疏表示系数αi1和αi2,

其中D采用文[9]中的通用字典。

(iv) 利用1-范数最大原则进行稀疏系数融合

得到最终的融合向量

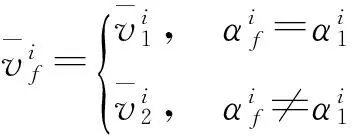
3) 高通子带的系数采用一致检验窗口中系数绝对值最大的原则[4]，即

vHf(i,j)={H1(i,j),|H1(i,j)|≥|H2(i,j)|;

H2(i,j),|H1(i,j)|<|H2(i,j)|

其中Hf(i,j) 是一致检验窗口的系数。

4) 去噪

利用文献[15]的阈值去噪原则，对融合后高通子带进行硬阈值处理，其阈值参数为：

1.1一般资料2016年12月至2017年2月我院对236例腹腔镜胆囊切除手术患者进行了研究分析,将患者分成了观察组和对照组,均有118例,观察组患者有50例男性和68例女性,最小34岁,最大58岁,平均(39.2±1.2)岁。对照组患者有52例男性,66例女性,最小35岁,最大59岁,平均(40.1±1.1)岁。两组患者的一般性资料对比不存在统计学差异性,能够进行对比分析。

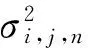
5) 利用剪切波逆变换得到融合去噪结果。

2 数值实验

2.1 测试图像

为了测试本文所提方法的有效性，图1给出了不同的6组测试图像。

2.2 图像融合效果的客观评价指标

为了衡量算法的性能，我们采用5个客观评价指标从不同角度对融合结果进行了量化评价，分别为熵(entropy,EN)，标准偏差(standarddeviation,SD)，互信息(mutualinformation,MI)[16]以及基于结构相似度的梯度QG评价指标[17]，这4种指标的值越大说明融合效果越好。

在噪声级别分别为0, 5, 10, 15 和20的高斯加性噪声所污染的源图像上进行实验，所提出的算法 (STSR)与DWT[4],CVT[5],SR[11],ST[6]和AST[12]方法进行比较。DWT和CVT方法的分解级数均为4，剪切波滤波器采用Meyer滤波器，大小分别为32×32和16×16，从细到粗分别选取剪切方向为16，16，8和8个。

图2给出一组噪声级别为σ=10的医学融合效果图的例子。我们发现对医学图像C1和C2的融合中，明显的看到所提方法STSR能很好的提高对比度，并且保留细节，在融合的结果很清楚的看到大脑中的软组织。

表1给出了各个方法在不同的噪声级别下在测试图集上的各个指标的平均值。表1显示，EN,SD,MI指标在几种方法中值是最高的，这表明，所提方法能保留源图像更多的平均信息，增强对比度，保留各个源图像的自身信息，QG随着噪声的增加它的值越高，这表明在这种情况下所提方法能很好的保留边缘信息。

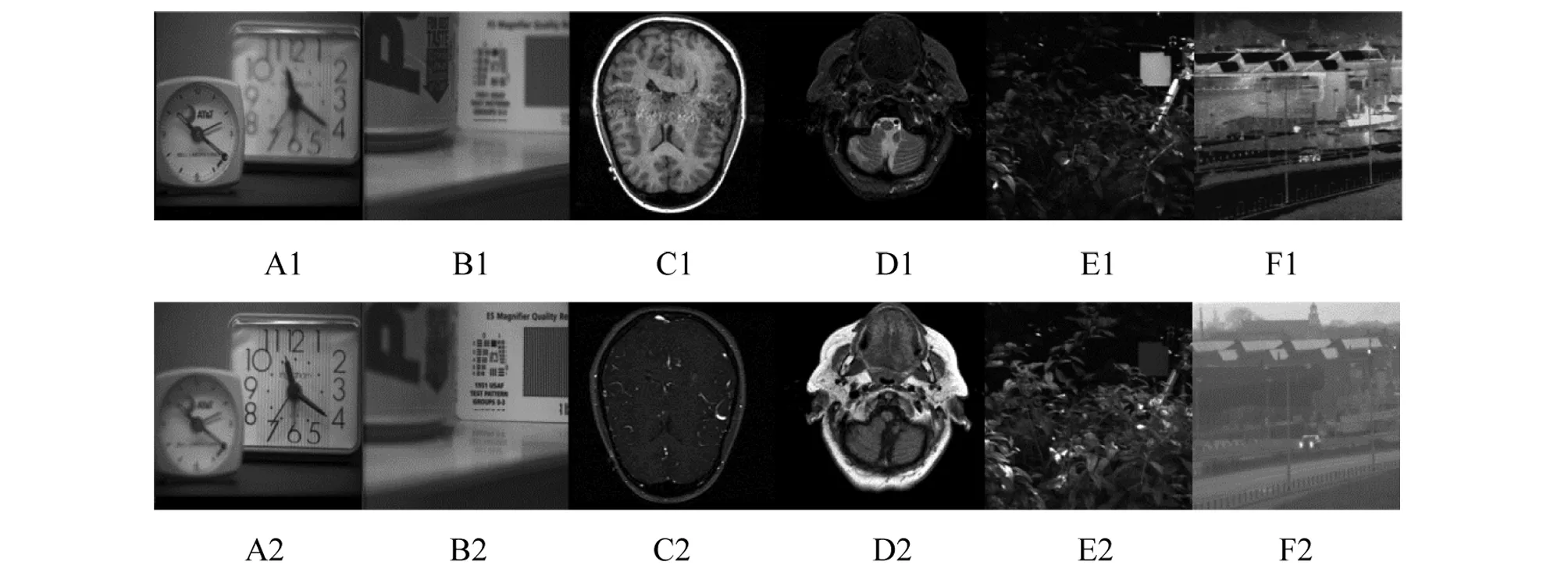
图1 测试集
Fig.1 Testing images

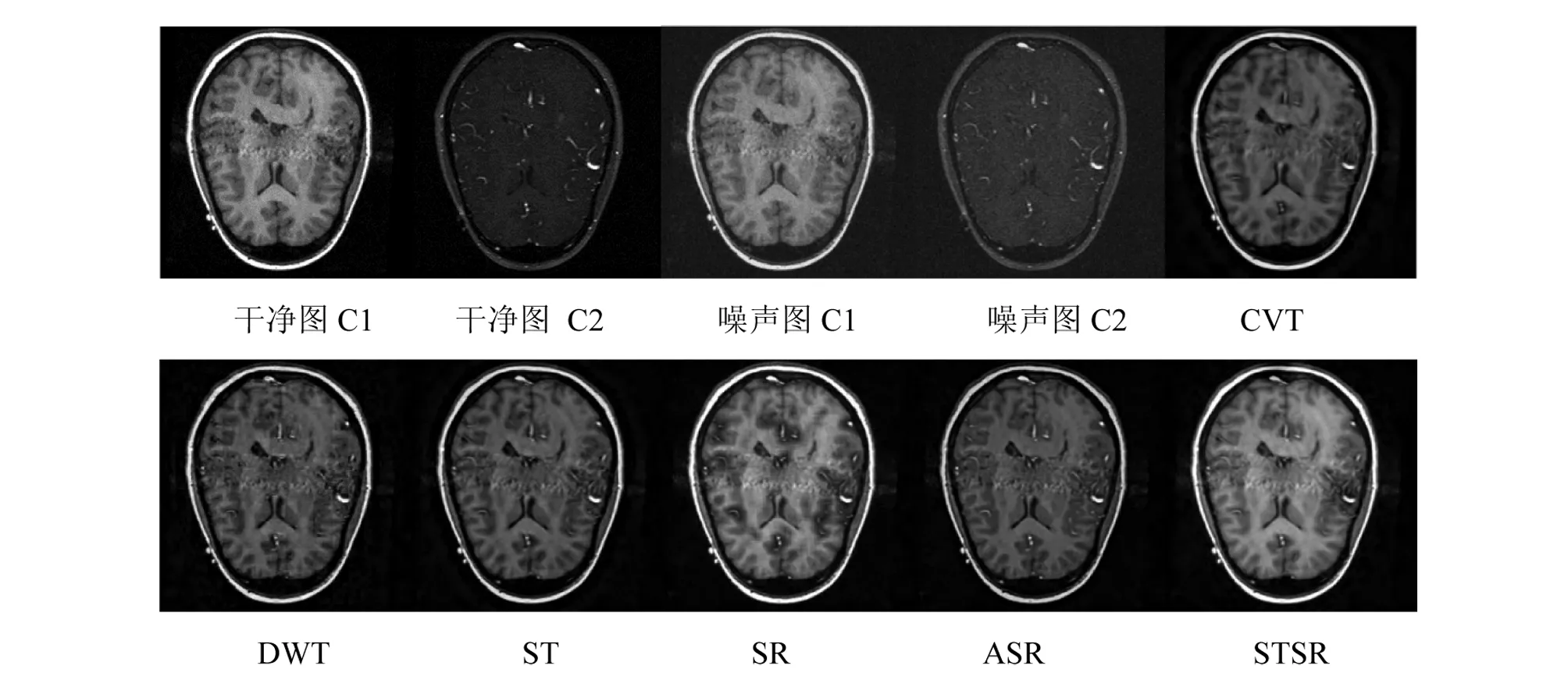
图2 σ=10时各个方法对C1和C2 的融合结果 Fig.2 Fused results of different fusion methods for images C1 and C2 with σ=10

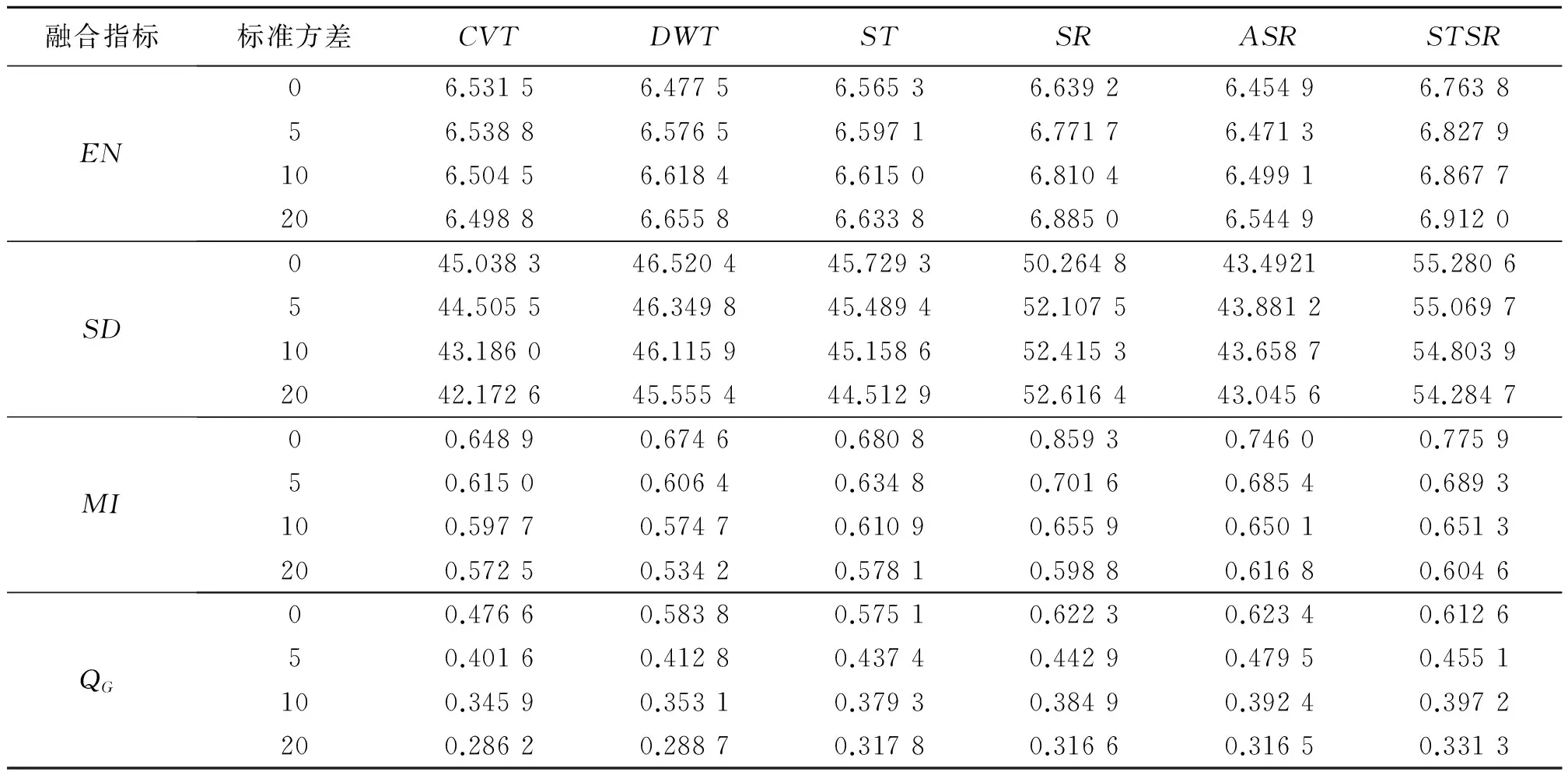
融合指标标准方差CVTDWTSTSRASRSTSREN06.53156.47756.56536.63926.45496.763856.53886.57656.59716.77176.47136.8279106.50456.61846.61506.81046.49916.8677206.49886.65586.63386.88506.54496.9120SD045.038346.520445.729350.264843.492155.2806544.505546.349845.489452.107543.881255.06971043.186046.115945.158652.415343.658754.80392042.172645.555444.512952.616443.045654.2847MI00.64890.67460.68080.85930.74600.775950.61500.60640.63480.70160.68540.6893100.59770.57470.61090.65590.65010.6513200.57250.53420.57810.59880.61680.6046QG00.47660.58380.57510.62230.62340.612650.40160.41280.43740.44290.47950.4551100.34590.35310.37930.38490.39240.3972200.28620.28870.31780.31660.31650.3313

3 结 论

本文利用剪切波变换结合高频局部窗口的一致性验证方法和低频稀疏表示的融合规则，对6种不同的图像进行融合，实验结果表明所提方法优于传统的多尺度方法CVT、DWT、ST和先进的稀疏表示方法SR和ASR，进一步证明了该方法平衡了传统多尺度方法和稀疏表示方法的缺点。

[1]RATTGA,VEGAJ,MURARIA,etal.Imagefusion:advancesinthestateoftheart[J].InformationFusion, 2007, 8(2):114-118.

[2]ELTOUKHYHA,KAVUSIS.Acomputationallyefficientalgorithmformulti-focusimagereconstruction[C]∥ProcSPIEElectronImaging, 2003, 5017: 332-341.

[3]LIS,YANGB.Multifocusimagefusionusingregionsegmentationandspatialfrequency[J].ImageandVisionComputing, 2008, 26(7): 971-979.

[4]LIH,MANJUNATHBS,MITRASK.Multisensorimagefusionusingthewavelettransform[J].GraphicalModelsandImageProcessing, 1995, 57(3): 235-245.

[5]NENCINIF,GARZELLIA,BARONTIS,etal.Remotesensingimagefusionusingthecurvelettransform[J].InformationFusion, 2007, 8(2):143-156.

[6]GAOG,XUL,FENGD.Multi-focusimagefusionbasedonnon-subsampledshearlettransform[J].IETImageProcessing, 2013, 7(6): 633-639.

[7]YANGB,LIS.Pixel-levelimagefusionwithsimultaneousorthogonalmatchingpursuit[J].InformationFusion, 2012, 13(1): 10-19.

[8]YUN,QIUT,BIF,etal.Imagefeaturesextractionandfusionbasedonjointsparserepresentation[J].IEEEJournalofSelectedTopicsinSignalProcessing, 2011, 5(5): 1074-1082.

[9]LIUY,LIUS.WANGZ.Ageneralframeworkforimagefusionbasedonmulti-scaletransformandsparserepresentation[J].InformationFusion, 2015, 24: 147-164.

[10]YINH,LIS,FANGL.Simultaneousimagefusionandsuper-resolutionusingsparserepresentation[J].InformationFusion, 2013, 14(3): 229-240.

[11]YANGB,LIS.Multifocusimagefusionandrestorationwithsparserepresentation[J].IEEETransactionsonInstrumentationandMeasurement, 2010, 59(4): 884-892.

[12]LIUY,WANGZ.Simultaneousimagefusionanddenoisingwithadaptivesparserepresentation[J].IETImageProcess, 2014, 9(5): 347-357.

[13]GUOK,LABATED.Optimallysparsemultidimensionalrepresentationusingshearlets[J].SiamJournalonMathematicalAnalysis, 2007, 39: 298-318.

[14]MALLATSG,ZHANGZ.Matchingpursuitswithtime-frequencydictionaries[J].IEEETransactionsonSignalProcessing, 1993,41(12): 3397-3415.

[15]DACA,ZHOUJ,DOM.Thenonsubsampledcontourlettransform:theory,design,andapplications[J].IEEETransactionsonImageProcessing, 2006, 15(10): 3089-3101.

[16]XYDEASCS,PETROVICV.Objectiveimagefusionperformancemeasure[J].ElectronicsLetters, 2000, 36(4): 308-309.

[17]LIUZ,BLASCHE,XUEZ,etal.Objectiveassessmentofmultiresolutionimagefusionalgorithmsforcontextenhancementinnightvision:acomparativestudy[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2012, 34 (1): 94-109.

Fusionmethodbasedonshearlettransformandsparserepresentation

CHANGLihong

(InstituteofMathematicsandInformationScience,BaojiUniversityofArtsandSciences,Baoji721013,China)

In order to further impoove noisy image fusion effect, a novel fusion method for noise image based on shearlet transform and sparse representation is presented. The proposed scheme performs the four stages: ① Perform a shearlet transform decomposition of each source image and obtain their low-pass and high-pass coefficients; ② Obtain the fused shearlet transform coefficients in the low-pass bands with a sparse representation based fusion approach while in the high-pass bands by fusing the largest absolution values; ③ The hard thresholding is applied to the fusion shearlet transform coefficients. ④ The result image is obtained by the inverse shearlet transform. Experimental results show that the proposed algorithm for image fusion is very effective.

image fusion; shearlet; sparse representation; multi-scale transform

10.13471/j.cnki.acta.snus.2017.04.003

2016-10-27 基金项目：国家自然科学基金(61362029,61379030)

常莉红(1980年生)，女；研究方向：稀疏表示和变分方法在图像处理中的应用；E-mail:changlihong-1999@126.com

TP

A

0529-6579(2017)04-0016-04