IIR数字滤波器在电机转速测量中的应用

杜仁慧,陶春荣,张 伟，施永柱

(中国船舶重工集团公司第七二四研究所,南京211153)

IIR数字滤波器在电机转速测量中的应用

杜仁慧,陶春荣,张 伟，施永柱

(中国船舶重工集团公司第七二四研究所,南京211153)

针对伺服系统中电机转速测量环节存在量化误差等噪声的问题,设计了3种无限冲激响应(IIR)数字滤波器。根据电机转速数据的特点给出了3种低通数字滤波器的设计方法,并通过仿真比较了其滤波性能。在此基础上,选择其中性能最好的椭圆滤波器对实际系统中的电机转速进行滤波。实验结果表明,该滤波器可以有效地减小电机转速测量噪声的影响,明显提高转速的稳态精度,而且具有结构简单、易于工程实现的优点。

伺服系统;转速测量;IIR数字滤波器

0 引 言

随着机扫雷达目标测向能力的不断提升,对伺服控制系统中电机转速的稳态精度提出了更高的要求。伺服电机一般采用数字控制方式,通过对旋转变压器等位置传感器检测的电机转子位置进行差分来计算电机的转速。[1]。而通常位置传感器的分辨率有限,经过直接差分得到的电机转速值受传感器量化误差等因素的影响会出现较大的噪声,这会严重影响电机转速的稳态精度。所以,需要研究合适的滤波方法来削弱这种转速噪声的影响,以实现电机的高稳态转速性能,从而使得伺服系统能够满足雷达整机对目标的测向精度要求。

针对伺服控制系统中电机转速的滤波问题,工程实现大都采用一些简单的数字滤波方法,如限幅滤波法、算术平均滤波法、滑动平均滤波法、中位值平均滤波法等。[2]这些方法原理简单,但其滤波后数据的精度不高。[3]此外,国内外的学者在研究电机转速滤波问题时也提出了一些其他有效的滤波算法,如线性相位滤波算法[4]、模糊自适应滤波算法[5]、卡尔曼滤波算法[6-7]等。这些基于现代滤波理论的滤波算法的滤波效果较好,但是有的需要基于系统的具体数学模型设计,算法较为复杂,对微处理器的要求较高,不易于工程实现。

无限冲激响应(IIR)数字滤波器具有结构简单、运算速度快、滤波精度高和选频特性好等优点,因而在各个领域得到了广泛的应用。[8-11]本文采用IIR数字滤波器对电机转速进行滤波处理,首先分析了3种典型IIR数字滤波器的幅频率特性,并给出了其设计方法;其次通过仿真比较了这3种滤波器对电机转速数据进行滤波的效果;最后根据比较的结果选择采用椭圆数字滤波器在实际系统中进行验证。结果表明,该滤波器的引入能够显著提高电机转速的稳态精度。

1 IIR数字滤波器设计

1.1 IIR数字滤波器简介

数字滤波器本质上是一个线性非时变离散系统,其输入输出都是离散时间信号,一般都是通过一系列加法运算和乘法运算来实现的。它的基本工作原理是利用离散系统特性对系统输入信号进行加工和变换,改变输入序列的频谱或信号波形,让有用频率的信号分量通过,抑制无用的信号分量。[10]其中,IIR数字滤波器的特点是具有无限持续时间的冲激响应,一般需要用递归模型来实现,因而又被称为递归滤波器,其系统传递函数表示为

(1)

式中,N为IIR滤波器传递函数的极点数,即滤波器的阶数;M为滤波器系统传递函数的零点数;ak和bk为滤波系数。其在数字系统中的差分方程表示为

(2)

其中x(n)、y(n)分别为输入和输出时域信号序列。

1.2 IIR数字滤波器设计方法

设计IIR数字滤波器时通常以模拟滤波器为原型,再将模拟滤波器转换为数字滤波器。模拟滤波器的理论和设计方法已发展得相当成熟,典型的有巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器等。IIR数字滤波器的一般步骤如下:

(1) 确定模拟滤波器的技术指标,主要包括通带截止频率ωc、阻带截止频率ωs、通带最大衰减αc、阻带最小衰减αs;

(2) 根据这些技术指标确定滤波器的最小阶数N和固定频率ωn;

(3) 利用最小阶数N产生模拟低通滤波原型;

(4) 利用固有频率ωn把模拟低通滤波器原型转换成模拟低通、高通、带通或带阻滤波器;

(5) 利用冲激响应不变法或双线性不变法把模拟滤波器转换成数字滤波器。

1.3 典型IIR数字滤波器的幅频特性比较

典型的IIR数字滤波器有巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器。本文拟采用这3种滤波器对电机转速进行滤波处理。为了直观地比较这3种滤波器的幅频特性,在相同的低通滤波器参数条件下绘制出它们的幅频特性曲线。3种低通滤波器的参数都取为ωc=200Hz,ωs=300Hz,αc=0.5dB,αs=35dB。

3种滤波器的幅频特性如图1所示,可以看出巴特沃斯滤波器的特点是在通带内的幅频响应曲线最大限度平坦,而在阻带则逐渐下降为零。因此,巴特沃斯滤波器又称“最平幅频响应”滤波器,而且也是最简单的滤波器。

切比雪夫滤波器幅频响应的通带部分不是单调下降,而是等波纹波动。其过渡带比巴特沃斯滤波器的衰减快,而且和理想滤波器的频率响应曲线之间的误差最小,但是它的通频带内存在一定幅度波动。这是不可避免的,也是过渡带衰减更快的代价。

图1 3种IIR数字滤波器的幅频特性曲线

椭圆滤波器幅频响应在通带和阻带内都是等波纹的。对于给定的阶数和波纹要求,椭圆滤波器能获得较其他滤波器更窄的过渡带宽。与切比雪夫滤波器相比,它在过渡带的下降斜度更大。一般情况下,椭圆滤波器能以最低的阶数实现指定的性能指标,所以它在信号处理中的应用更广泛。

2 电机转速滤波的仿真研究

本文需要进行滤波处理的电机转速信号是根据电机转子位置采用M法计算得到的,其采样频率Fs=1 000 Hz。上面提到的3种典型的IIR数字滤波器都可以实现对电机转速信号的滤波处理。所以,本节根据电机转速数据的特点,选择合适的参数设计不同的数字滤波器进行对比,以选择效果最佳的数字滤波器。

仿真时发现同一类型的IIR数字滤波器都具有这样的规律:随着通带截止频率ωc的减小,滤波后的转速曲线在动态过程的滞后越来越大,但稳态过程的精度越来越好。考虑到系统的速度环带宽不能小于100 Hz,故设计3种IIR数字滤波器时都取如下参数值:

得到的3种数字滤波器的滤波系数如下:

(1) 巴特沃斯滤波器为6阶。

a1=-2.5779, a2=3.2843, a3=-2.4066,

a4=1.0569, a5=-0.2590, a6=0.0275,

b0=0.0020, b1=0.0117, b2=0.0294,

b3=0.0391, b4=0.0294, b5=0.0117,

b6=0.0020

(2) 切比雪夫滤波器为4阶。

a1=-2.6339,a2=3.0380,a3=-1.7299,

a4=0.4078,b0=0.0048,b1=0.0194,

b2=0.0291,b3=0.0194,b4=0.0048

(3) 椭圆滤波器为3阶。

a1=-1.7289,a2=1.3918,a3=-0.3810,

b0=0.1547,b1=-0.0138,b2=-0.0138,

b3=0.1547

可以看出椭圆滤波器的阶数最低。采用这3种滤波器对幅值为2 400 r/min的转速阶跃信号进行滤波处理,仿真结果如图2～图3所示。

从仿真结果可以看出,本文设计的3种IIR数字滤波器都滤去了转速信号在稳态时的噪声,使稳态性能得到了较大的改善(图3)。而在动态过程几乎没有引入超调,只是响应有一点滞后,但不是很明显(图2),具体性能指标如表1。

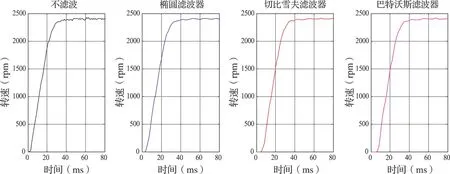
图2 3种数字滤波器在动态过程的滤波效果比较

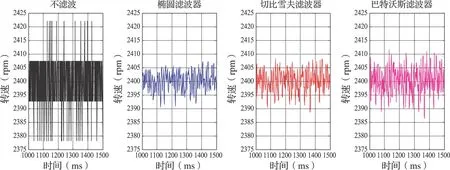
图3 3种数字滤波器在稳态过程的滤波效果比较

表1 滤波前后的转速性能指标

从表1的数据可以看出,经过椭圆滤波器处理的转速动态响应滞后最小,稳态精度最高。所以,用椭圆滤波器对电机转速进行滤波的效果最好,切比雪夫滤波器的性能次之,而巴特沃斯滤波器的性能最差。

3 电机转速滤波的实验研究

上节的仿真研究验证了所设计的3种IIR数字滤波器的可行性,并得出椭圆滤波器滤波效果最好的结论,而且椭圆滤波器还有阶数最低、更易于工程实现的优势。所以,本节将所设计的椭圆滤波器应用于实际的电机伺服控制系统进行实验验证。

实际系统中椭圆数字滤波器的滤波参数跟仿真时取一样的值,采用TI公司型号为TMS320F38335的浮点数字信号处理器实现。实验时电机转速的采样频率Fs=1 000 Hz,引入椭圆滤波器时不改变速度环的控制器参数,且采用滤波后的数据进行速度闭环控制,得到幅值为2 400 r/min的转速阶跃响应,如图4～图5所示。

图4 滤波前后转速响应动态过程比较

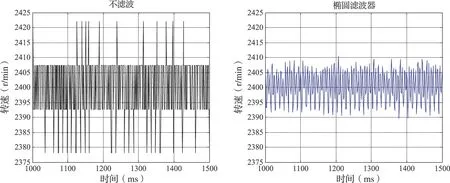
图5 滤波前后转速响应稳态过程比较

从实验结果可知,经过椭圆滤波器处理后,转速响应在动态部分有1.05%的超调,上升时间为27 ms,即有2 ms的滞后,这都在可以接受的范围内;稳态部分转速均匀,误差范围为-10.44～10.32 r/min,即稳态精度为-0.43%～0.43%,与滤波前相比提高了约0.5%。所以,椭圆滤波器的引入提高了电机转速的稳态性能。

4 结束语

本文主要研究了伺服系统中电机转速的滤波问题,根据电机转速数据的特点设计了3种IIR低通数字滤波器。通过仿真比较了这3种数字滤波器的性能,结果表明椭圆滤波器对电机转速的滤波效果最好且阶数最低。通过实验分析了椭圆滤波器的实际滤波效果,结果表明所设计的椭圆滤波器能够明显削弱电机转速测量噪声的影响,提高电机转速的稳态精度。

[1] Sheng-Ming Yang,Shuenn-Jenn Ke.Performance Evaluation of a Velocity Observer for Accurate Velocity Estimation of Servo Motor Drives[J].IEEE Trans.On Industrial Aplications,2000,36(1):98-104.

[2] 蔡登胜,罗维,赵明辉.发动机转速信号的检测及数字滤波方法[J].工程机械,2012,43(1):19-24.

[3] 余志强,刘建华,何朝峰,刘宁宁,石彦辉.巴特沃兹数字滤波及其在智能测控系统中的应用[J].电测与仪表,2007,44(5):5-8.

[4] Zhi Gao,Larry Turner,Roy S Colby.Application of Linear-Phase Filters in Induction Motor Speed Detection[C]// IEEE Conference on Energy Conversion Congress and Exposition,2012:1314-1321.

[5] 申水文,张建武.模糊滤波技术在转速信息处理中的应用[J].上海交通大学学报,1998,32(5):138-141.

[6] 肖曦,王伟华,吕志鹏.一种基于增量式卡尔曼滤波器的PMSM转速滤波算法[J].电机与控制学报,2014,18(10):104-110.

[7] Murat Barut,Seta Bogosyan,Metin Gokasan.Speed-Sensorless Estimation for Induction Motors Using Extended Kalman Filters[J].IEEE Trans.on Industrial Electronics,2007,54(1):272-280.

[8] 沈彦杰,樊昌,佟胜喜,秦加成,李元首.椭圆数字滤波器在动态风洞试验中的应用[J].航空计算技术,2011,41(1):120-122.

[9] Singh R,Arya S k.Optimization of IIR digital filters using Particle Swarm Optimization[C]// International Conference on Communication,Information & Computing Technology,2012:1-7.

[10] 王易炜,张金鹏,王 龙.基于MATLAB的数字滤波器设计及其在数据处理中的应用[J].航空兵器,2011,47(4):43-47.

[11] Lyons R.Improved narrowband low-pass IIR filters in fixed-point systems[J].Signal Processing Magazine,2009,26(2):128-132.

征 订 启 事

本刊已参加“全国非邮发报刊联合征订”，请本刊读者直接向联合征订服务部汇款订阅。

通信地址：天津市卫津南路李七庄邮局9801信箱

邮编：300381

网址：www.LHZD.com

E-mail:wms@lhzd.com; LHZD@public.tpt.tj.cn

电话及传真：(022)23973378 23962479

《雷达与对抗》编辑部

Application of IIR digital filters in motor speed measurement

DU Ren-hui, TAO Chun-rong, ZHANG Wei, SHI Yong-zhu

(No.724 Research Institute of CSIC, Nanjing 211153)

In view of the noise problem caused by quantization error in the motor speed measurement for the servo system, the three infinite impulse response (IIR) digital filters are designed. According to the characteristics of the motor speed data, the design of the three low-pass digital filters is given, with filter performances compared via the simulation. The elliptic filter with the optimal performance is selected to filter the motor speed in real system. The test results indicate that the filter can effectively reduce the effect of noise in the motor speed measurement, remarkably improving the steady-state precision, and it features simple structure and easy engineering implementation.

servo system; speed measurement; IIR digital filter

2017-03-28;

2017-04-07

杜仁慧(1985-)，男，高级工程师，博士，研究方向：控制理论与控制工程；陶春荣(1980-)，男，高级工程师，硕士，研究方向：控制理论与控制工程；张伟(1981-)，男，高级工程师，硕士，研究方向：控制理论与控制工程；施永柱(1987-)，男，工程师，硕士，研究方向：控制理论与控制工程。

TN713.7

A

1009-0401(2017)02-0064-05