基于多普勒频率的目标定位算法

郭新民,赵丹辉

(1. 92785部队,河北 秦皇岛 066000;2. 北京理工大学 信息与电子学院, 北京 100081)

基于多普勒频率的目标定位算法

郭新民1,2,赵丹辉1

(1. 92785部队,河北 秦皇岛 066000;2. 北京理工大学 信息与电子学院, 北京 100081)

针对近程高速运动目标,提出了一种基于长基线短距离条件下利用单发多收(Single-Input Multiple-Output, SIMO)雷达系统获得多普勒频率进行目标定位的方法:基于SIMO连续波雷达提取目标的多普勒频率,根据矢量矩阵方程建立最优化函数,采用网格搜索法进行非线性优化处理。仿真结果表明该方法可以得到具有较高精度的定位结果。

多普勒频率;目标定位;单发多收

0 引 言

精确打击武器在现代高科技战争中发挥着重要作用。为了准确地鉴定精确打击武器的性能,在攻击过程的末段需要实时地测量打击武器与靶标之间的相对空间位置与相对速度,还原其攻击靶标末段的相对运动轨迹,即运动目标的空间实时定位,为打击武器命中精度的现场评判与事后的数据分析及处理打下坚实的基础。[1-3]在对空间目标的主动探测定位方法中,基于多普勒频率的目标定位方法对信号形式的要求较为简单,且对时延的精度要求不高而逐步引起人们重视。[4-6]基于多普勒频率的目标定位实质上是一个非线性优化过程。文献[7]利用目标回波信号的多普勒频率对二维平面内的运动目标进行了定位分析,但并未充分地利用目标的运动特性。针对近程高速运动目标在长基线短距离条件下的定位需求,本文提出了一种基于多普勒频率的单发多收雷达系统目标定位算法。

1 多站多普勒频率定位原理

本算法采用正弦调频连续波信号,相比传统的连续波多普勒体制,信号泄漏的抑制能力更强,灵敏度更高。正弦调频连续波雷达的基本工作原理如图1所示[8]。

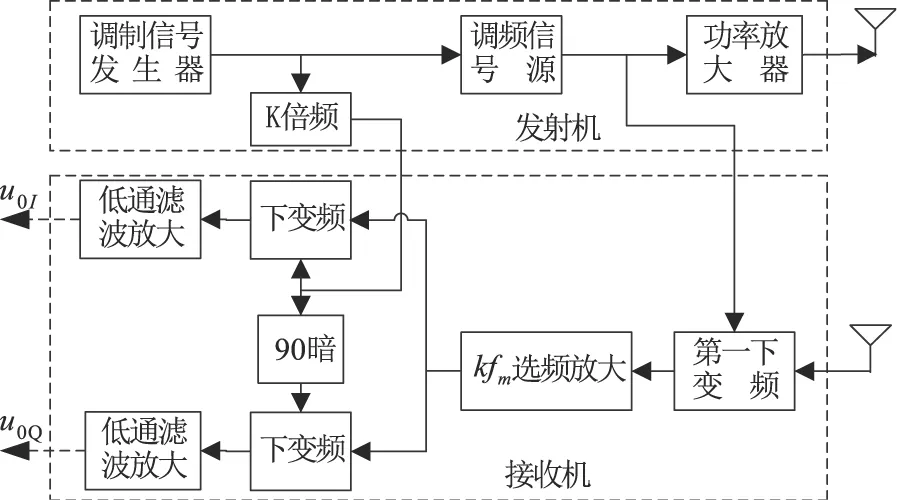
图1 正弦调频连续波雷达原理框图

雷达将接收到的回波信号与发射机耦合出的信号经第一下变频混频输出差频信号,经选频放大器滤波、放大,再将其与倍频器输出信号在下变频中混频,经低通滤波放大后提取出多普勒频率信息,具有较高的精度。[9]

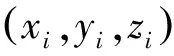
(1)

向量P0-Ri的方向余弦为

(2)

图2 目标与收发天线站的位置关系

多普勒频率是由于目标与雷达之间产生相对运动而产生。根据多普勒原理,对于收发分置的雷达系统,当目标运动速度远小于光速时,雷达某一接收天线站收到的目标回波信号的多普勒频率可表示为

(3)

其中,fdi是第i个接收天线收到的回波信号的多普勒频率,v是目标与雷达之间的相对速度,θT是目标运动速度与目标和雷达发射站之间连线的夹角,θRi是目标运动速度与目标和雷达第i个接收站之间连线的夹角,λ是雷达发射信号的波长,则两个雷达接收天线收到的回波信号的多普勒频率差为

其中,θRj是目标运动速度与目标和第j个接收站之间连线的夹角,θRi是目标运动速度与目标和第i个接收站之间连线的夹角。

两个雷达天线站接收到的目标回波信号的频率差值可表示为

(5)

式中vx,vy,vz是速度v在各个坐标轴上的向量。对回波信号进行处理可提取出频率fi,通过对非线性方程组求解即可得出目标位置。

(6)

其中,NR代表接收雷达的个数,θk代表第k时刻目标的位置:

(7)

2 基于SIMO的TLDF算法

基于多普勒频率的目标定位(TargetLocalizationviaDopplerFrequency,TLDF)算法是利用目标回波的多普勒频率信息对目标的位置和速度进行较精确的估计,其主要实现方法是从接收的回波信号中提取多普勒频率信息并以矢量矩阵的形式存储在网格交叉点处,利用获得的所有矢量矩阵方程得到最优化函数,最后利用网格搜索法求解最优化函数,即可得出目标位置和速度矢量的最优解。

假设一个SIMO雷达系统由1个发射站、NR个接收站组成,站间距离较远,且目标到各站的距离处于同一个数量级。假设目标以速度V运动,发射站发射的信号频率为f0,则第l个接收站收到的回波信号频率为[10-11]

(8)

其中,c是光速,fl表示第l个接收站收到的回波信号频率。式(8)中,余弦角度的值用目标、发射站、接收站的位置及目标速度表示可得

(9)

(10)

将式(9)、(10)代入式(8)中,移相并化简得

(11)

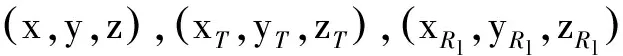
假设NR个接收站接收的信号频率分别记为f1,f2,f3,…,fNR。将前3个雷达划分为第1组,其余雷达为第2组,得矢量矩阵方程:

cb1=-A1v,cb2=-A2v

(12)

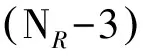
令

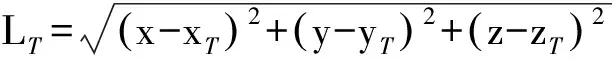
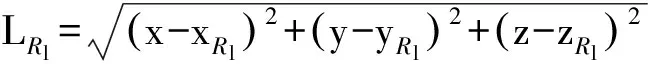
l=1,2,…,NR

通过求解矩阵方程即可得到目标位置。由于方程具有高度非线性,须构造一个目标优化函数,采用网格搜索法进行求解[12]。目标速度可写为

(13)

将式(13)代入式(12)得

(14)

进而得到目标优化函数为

(15)

式中,矩阵A1取的是前3个接收站,此时矩阵A1为方阵。A1亦可取多个接收站,其个数N需满足条件:3≤N≤NR-3。式(15)的目标优化函数是使频率估计误差最小,即通过所有可能的目标位置计算得到的多普勒频率最大限度地接近所提取到的频率,则具有最小频率误差的位置被选出,作为最终估算的目标位置。

3 仿真分析

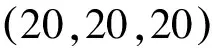
图3为多普勒频率的提取误差。图4为目标运动到水平面前各时刻的目标定位及速度估计的仿真结果,目标估计值为500次独立仿真结果的平均值。图4中将基于TLDF算法及最小二乘法的定位结果与目标真实状态进行比较,可看出基于TLDF算法的定位结果很精确,目标的定位精度在2 m以内,速度的估计误差在10 m/s以内。图5表示出采用TLDF算法估计的目标位置与其真实位置相比较的三维空间图,同时表示出各收发天线站的位置及目标相对于收发天线的运动过程。图6表示初始时刻目标优化函数的四维示意图,可以看出在测量区域内目标函数有唯一的极小值,采用格形搜索方法可以寻得唯一的最优解。

表1 SIMO系统收发站点坐标

图3 多普勒频率的提取误差

图4 目标位置及速度的定位结果

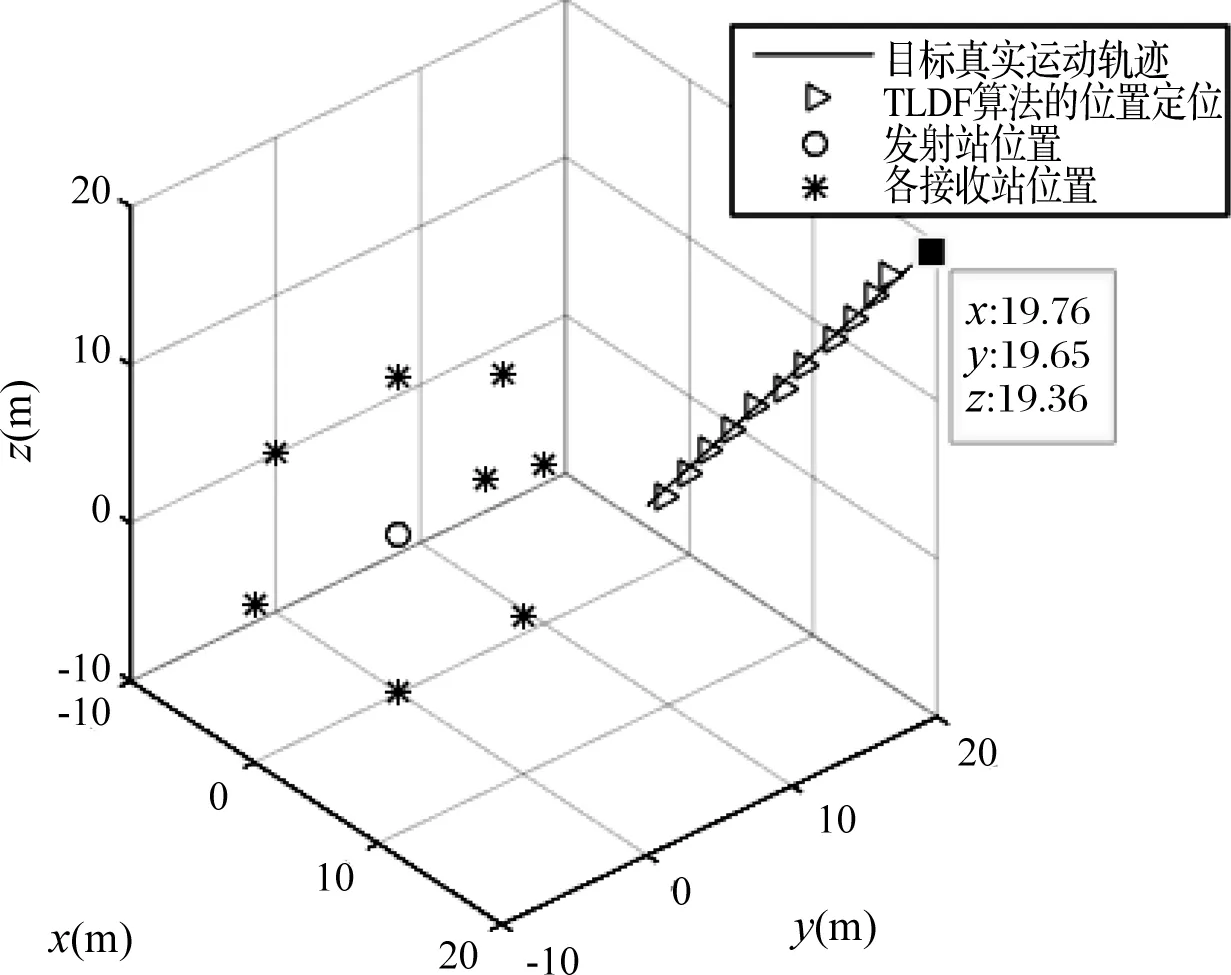
图5 SIMO系统的布局和目标定位结果

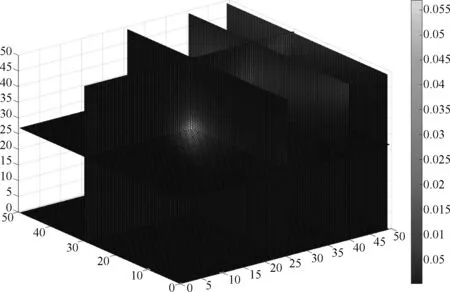
图6 目标函数的四维示意图

4 结束语

本文提出了一种在长基线短距离条件下基于多普勒频率对高速运动目标进行定位的方法。该方法基于SIMO雷达系统的天线阵布局,根据目标的运动特性,将不同接收天线测得的多普勒频率进行联合处理,建立非线性寻优过程,并对算法进行了计算机仿真。仿真结果表明:当高速运动目标距雷达35 m以内时,多普勒频率提取误差在50 Hz以内,目标的定位精度可达到2 m,速度的估计误差在10 m/s以内。该算法比较理想地实现了对近程高速运动目标的定位及速度的测量,具有较高的精度。

[1] Xiao Y C, Wei P, Yuan T. Observability and performance analysis of Bi/Multi-Static Doppler-Only Radar [J]. IEEE Transactions on Aerospace & Electronic Systems, 2010, 46(4): 1654-1667.

[2] Insanic E, Siqueira P R. A maximum likelihood approach to estimation of vector velocity in doppler Radar networks [J]. IEEE Transactions on Geoscience & Remote Sensing, 2012, 50(2): 553-567.

[3] Godrich H, Haimovich A M, Blum R S. Target localization techniques and tools for MIMO Radar [J]. IEE Radar, Sonar and Navigation Journal, 2009, 23(3): 30-35.

[4] Bekkerman I, Tabrikian J. Target detection and localization using MIMO Radars and Sonars [J]. IEEE Transactions on Signal Processing, 2006, 54(10): 373-383.

[5] Godrich H, Haimovich A M, Blum R S. Cramer Rao bound on target localization estimation in MIMO Radar systems [C]// IEEE 42nd Annual Conference on Information Sciences and Systems, 2008: 134-139.

[6] Wang Q, Deng X, Zhong D, et al. Observability requirements for emitter location via LBI phase difference measurements[C]//IEEE International Conference on Information and Automation, 2008: 854-858.

[7] Kalkan Y, Baykal B. Target localization and velocity estimation methods for frequency-only MIMO Radars[C]// IEEE Radar Conference,2011: 458-463.

[8] Xu J, He M H, Yu C L, et al. A new method of fixed single observer passive location based on phase difference Rate-of-Change[C]// IEEE Third International Conference on Measuring Technology and Mechatronics Automation, 2011: 174-177.

[9] 秦国栋,陈伯孝,陈多芳,等.双基地多载频MIMO雷达目标运动参数估计[J].系统工程与电子技术, 2009, 31(4): 799-803.

[10] 王丽,冯讯.基于空间分集的MIMO雷达目标跟踪算法研究[J].现代雷达, 2012, 34(5): 26-30.

[11] 袁汀.基于多普勒频率的可观测性分析及定位算法研究[D].成都:电子科技大学硕士论文, 2006.

[12] 冯定伟.多站分布式无线电脱靶量测量技术研究[D].北京:北京理工大学博士论文, 2013.

A target localization algorithm based on Doppler frequency

GUO Xin-min1,2, ZHAO Dan-hui1

(1. Unit 92785 of the PLA, Qinhuangdao 066000; 2. School of Information and Electronics, Beijing Institute of Technology, Beijing 100081)

A target localization algorithm is proposed for the short-range high-speed moving targets, in which the Single-Input Multiple-Output (SIMO) radar system is utilized to obtain the Doppler frequencies under the long-baseline and short-range condition. Based on the Doppler frequencies of the targets extracted by the SIMO CW radar, the vector matrix equation is used to establish the optimized function and the mesh search method is used for nonlinear optimization. The simulation results demonstrate that the proposed algorithm can obtain the high-precision target localization results.

Doppler frequency; target localization; SIMO

2017-04-26;

2017-05-19

郭新民(1984-),男,工程师,在读硕士,研究方向:雷达系统及其信号处理;赵丹辉(1984-),男,工程师,硕士,研究方向:雷达系统及其信号处理。

TN958

A

1009-0401(2017)02-0018-05