网络化联合作战体系OODA环路最大行动速度计算与仿真
徐 康,李华军,王盛超,申智利
(94005部队,甘肃 酒泉733306)
网络化联合作战体系OODA环路最大行动速度计算与仿真
徐 康,李华军,王盛超,申智利
(94005部队,甘肃 酒泉733306)
OODA环路这一重要的军事行为已经嵌入到网络作战的各个层次。为了度量计算OODA环路的最大运行速度ΛOODA,首先构建了网络化作战体系模型,给出了基于网络的作战体系信息交换速率的计算方法。通过量化OODA环路各阶段的时间消耗,进一步得到OODA环路最大运行速度的度量方法。最后通过MATLAB软件(LPIsimNet)仿真计算了网络电子攻击对网络化作战体系的影响效果。
OODA环路;网络化;联合作战体系;信息交换速率
0 引 言
观察-判断-决策-行动(OODA)环路是美国军事学家John Boyd提出的一种重要的军事行为,其核心思想是用来说明如何调动个人(作战部队)力量在战争中完全摧毁敌人而保存自己的实力。OODA环路能够快速处理整个环路的作战计划,对发生事件作出观察和反应的速度比对手快,还能渗透到对方的决策环路上,取得军事上的先机。[1]
随着现有传感器信息与网络技术水平的飞速发展,网络化的作战体系已经越来越多地应用在现代战争中,与此相适应的作战指挥模式也越来越多地采用网络化的OODA环路这一军事行为。在实际战争中,OODA环路的合理应用能够有效地提升信息处理能力,改善作战计划,同时指挥官的作战意图可以被快速阐述清楚。因此,OODA环路的最大运行速度ΛOODA[2]可用来评估网络作战体系的整体效能。影响ΛOODA的因素很多。由于作战体系总的信息处理能力的增强可以加快整体作战进程,从而影响了部队的机动性、决策速度、杀伤力和灵活性,因此作战体系中的信息处理能力是影响ΛOODA的重要因素。本文针对作战体系呈现网络化这一特点,采用网络拓扑结构对作战体系进行建模,给出了基于网络的作战体系信息交换速率的计算方法,最后提出了一种计算ΛOODA的度量方法,并通过MATLAB软件(LPIsimNet)仿真计算了网络电子攻击对网络化作战体系的影响效果。
1 网络化作战体系模型的构建[3]
由于OODA环路是一种网络化的军事行为,为了度量环路中的最大运行速度ΛOODA,其关键在于网络化作战体系模型的构建。在这里采用网络拓扑结构对作战体系进行建模。这里的网络就是指一个传感器网络,每个节点代表一个作战单元,可以是一个雷达系统或飞机系统等等,节点之间的联系就代表作战单元之间的关联。遵循OODA环路的概念,将网络化作战体系抽象为4类节点,分别为决策节点(D)、传感节点(S)、攻击节点(A)和目标节点(T)。[3]
节点之间的连接关系[3]约束如下:决策节点一般为指挥所、情报中心,因此D与D之间的连接是双向的,表示决策节点之间信息的共享。节点S和节点A只受单方的D指挥,其中传感节点侦察目标T的信息并传送给决策节点D,攻击节点A只接受D的控制对目标T进行打击摧毁。由此可以得到该网络作战体系的OODA过程如图1所示。
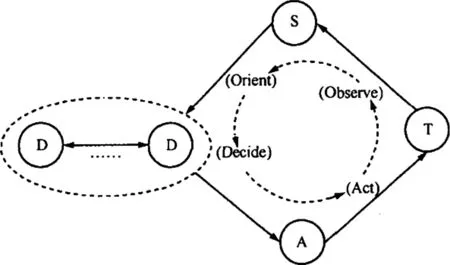
图1 基于网络化作战体系的OODA过程
图中,T代表敌方目标节点,A代表我方所有攻击节点,S代表我方所有传感节点。为了便于后面的仿真计算,采用信息能力值和信息处理速率来表征不同类型节点的权值。节点权值的大小表示该节点在作战体系中的作用,一般分配给D节点的值最大,S次之,A节点的权值最小。
网络的作战体系信息交换速率基于上述网络模型进行定义,计为λT,其表达式为[4]
(1)
其中[4]
(2)
(3)

2 OODA环路最大运行速度计算
从OODA环路的定义可以看出,其最大运行速度是由4个阶段共同决定的。图2给出了在4个不同阶段(观察、判断、决策、行动)影响ΛOODA的主要因素,以及这些因素彼此之间的关系。[7]
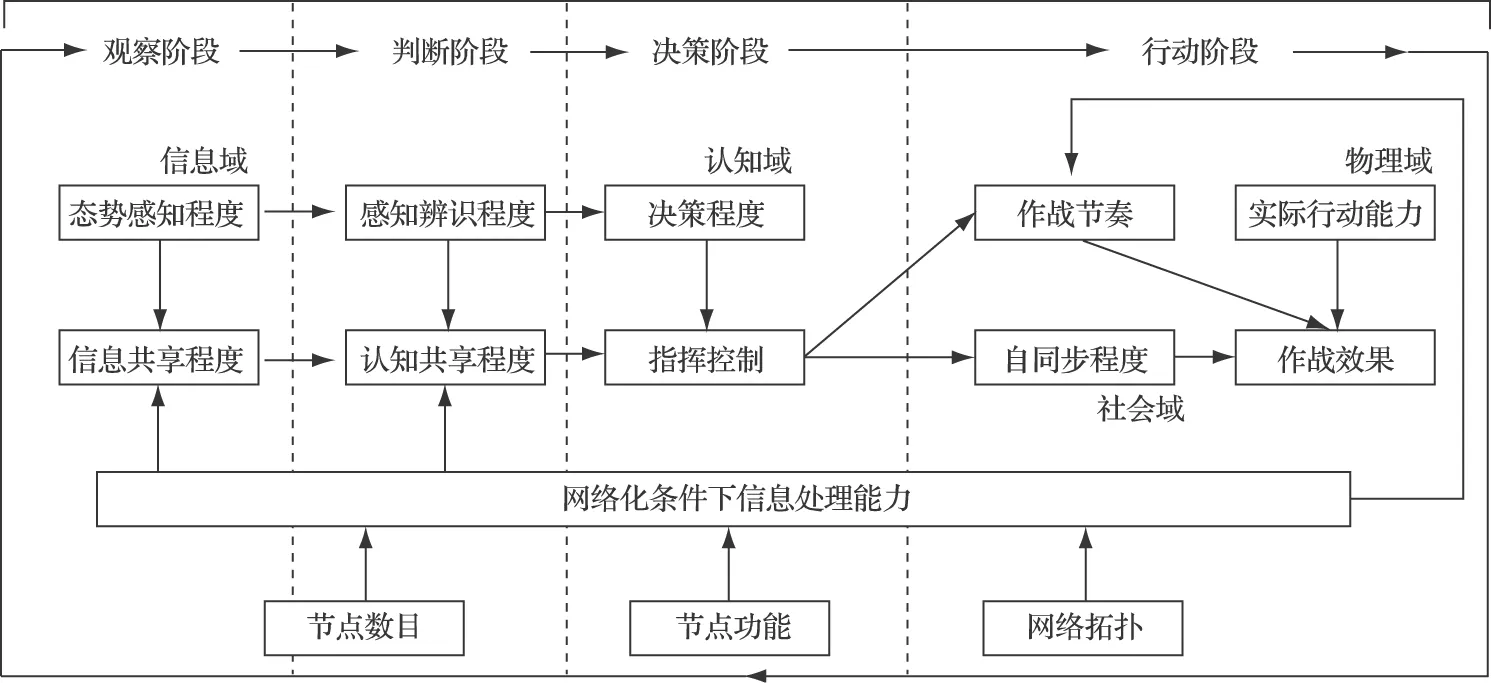
图2 影响ΛOODA的主要因素和这些因素彼此之间的关系
从图2可以看出,网络化的作战体系主要是基于网络空间取得信息优势,进而提高了战场环境的态势感知能力、指挥员的决策能力以及作战部队的行动能力,而且网络空间的信息处理能力对于除决策阶段的剩余三个阶段都有直接影响,可见网络作战体系的信息处理速度对OODA环路这一军事行为的重要性。这正是本文在计算ΛOODA之前构建网络化作战体系模型,并基于该模型给出网络的作战体系信息交换速率计算公式的主要原因。图3基于上述分析给出了ΛOODA分段度量模型[4]。

图3 OODA环路分段模型
图中,△t1定义为从观察到判断的时间,是传感器节点进行信息收集并传输给指挥所进行信息融合的过程[3],可直接由λT决定;△t2是从判断到决策的时间,这一过程主要与指挥员的能力和经验有关,由认知域的决策速度λC2决定,不能用λT衡量;△t3是从决策到行动的时间,它必须大于信息交换时间和部署时间(由物理域的部署速度[7]λd决定);△t4是从行动到下一次观察的时间,一般大于信息交换时间和战斗时间(由物理域的作战速度[7]λf决定)的总和。定义OODA环路总的消耗时间为TOODA[4],则有
(6)
在OODA环路速度参数中,最感兴趣的是ΛOODA。对式(6)求倒数[4]:
(7)
从式(7)可以看出,环路的最大运行速度受网络的拓扑结构(由λT决定)和整体决策速度、部署时间、作战时间限制。通过这样一个方程将网络作战体系内部度量标准和传感器与武器网络的运行结果直接联系起来,即将网络空间和作战指挥网络紧密地联系起来,可以直接用来评估网络化作战体系的信息优势和战场优势。
3 网络电子攻击效果度量
当网络化作战体系遭受电子攻击时,如果被攻击节点接收机的干扰信号比(JSR[4])超过了特定门限,使得网络链路的误比特率无法接受时,这时就无法建立起数据链路,进而影响了网络的最大运行速度。因此,通过仿真对JSR评估的意义重大。JSR在实际测量中受很多因素的影响,本文给出的是基于MATLAB程序集LPIsimNet仿真环境下的简易计算公式,为后面的仿真实验提供了理论评估基础,其表达式如下[4]:
(8)

4 仿真实验
仿真场景想定:我方一个导弹发射网络化作战体系由预警雷达(传感节点S)、空中无人机(决策节点D)、地面情报站(决策节点D)、地面指挥部(决策节点D)以及导弹发射单元(攻击节点A)组成,敌方一架电子干扰飞机同时对我方的作战体系中的两个节点进行电子干扰攻击以切断我方作战网络信息交换链路。场景实现:采用MATLAB程序集LPIsimNet对上述的想定场景进行参数设置,其仿真场景如图4。
图4为用MATLAB软件(LPIsimNet)对分布在10 000 km2范围内的想定场景进行仿真,其中节点1(DDFS)为导弹发射单元,节点2(WRJ)为无人机,节点3(ZHB)为我方指挥部,节点5(QBZ)为我方地面情报站,节点6(RADAR)为我方预警雷达,节点4(GRJ)为敌方干扰机。
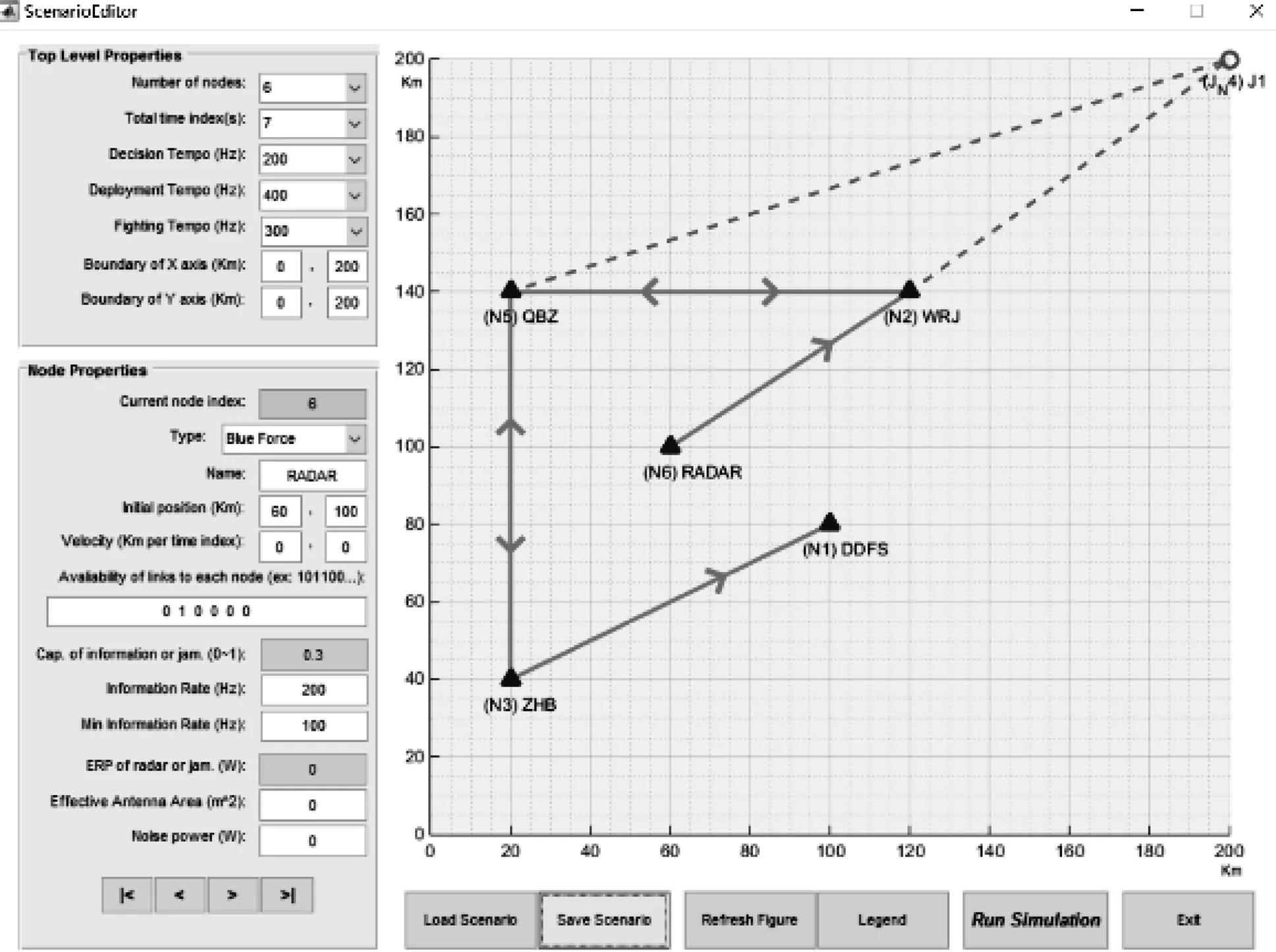
图4 仿真场景

表1 仿真场景的参数设置
仿真结果分析:在图4中设置总的时间序号数为7,当运行仿真时,根据时间序号,敌方干扰机以速度(-20,-10)接近节点2和节点5。位置以节点的初始位置为参考,速度表示每个节点在每时间序号的位移(km/时间序号)。在这里只给出时间序号1、2、6、7的仿真结果(这4个时间序号参考性高)。在时序1干扰机位于初始位置,从图5可以看到我方的作战网络没有受到任何影响,当干扰机以一定的速度逐渐接近节点2和节点5时,警告出现在时序2,干扰机的接近使得节点5至节点2以及节点6到节点2的链路中断,即同时切断了我方地面情报站和预警雷达至无人机的通信;当干扰机位于时序6位置时,从节点2至节点5的连接也受到了压制,导致链路中断,即我方地面情报站与无人机之间的双向通信完全被切断;最终当干扰机位于时序7位置时,节点3至节点5的链路也同时被中断,造成的后果是我方地作战指挥部无法向地面情报站传输信息,致使我方的导弹发射单元无法接收到正确的作战指挥命令,处于瘫痪状态。
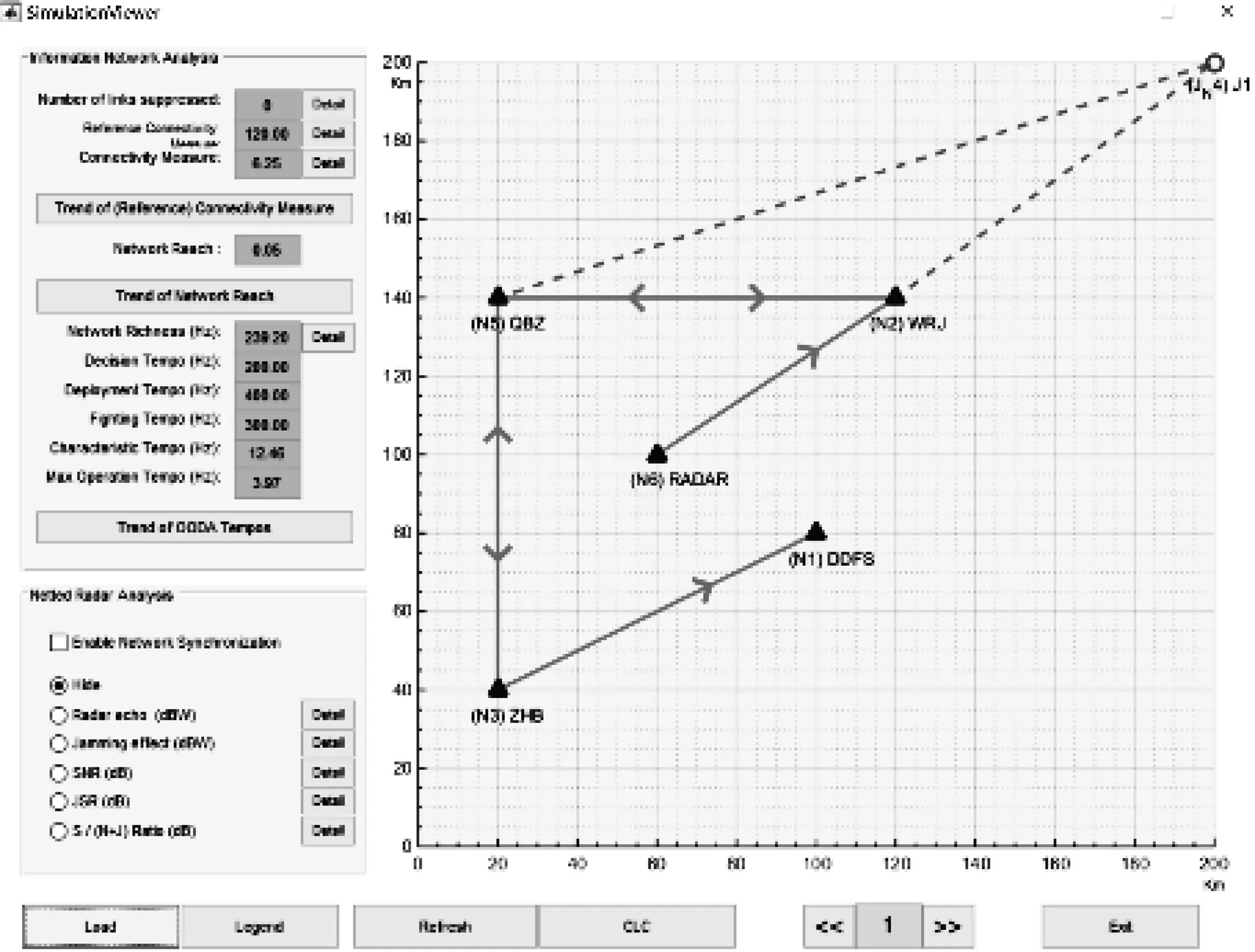
图5 在时序1的干扰仿真
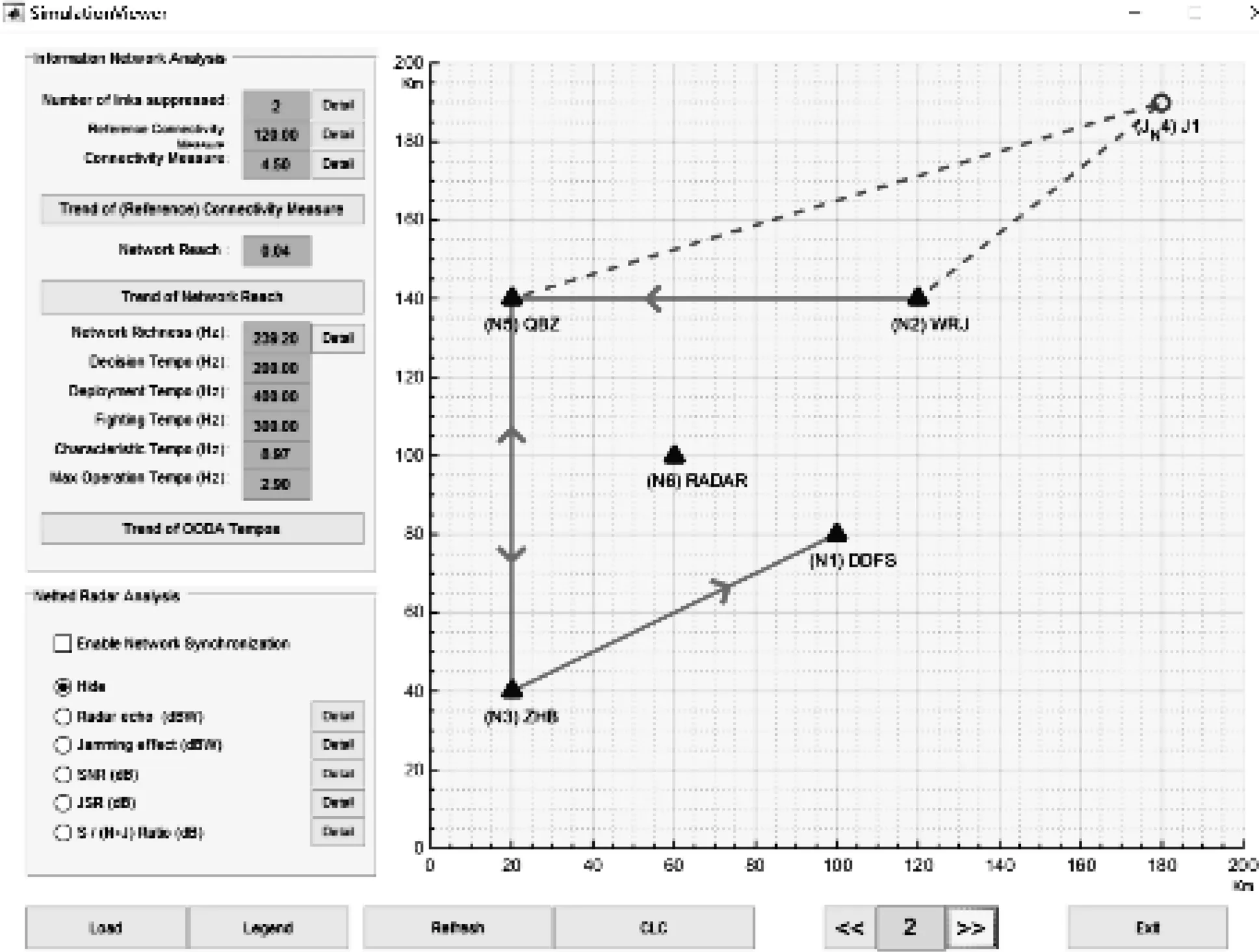
图6 在时序2的干扰仿真

图7 在时序6的干扰仿真
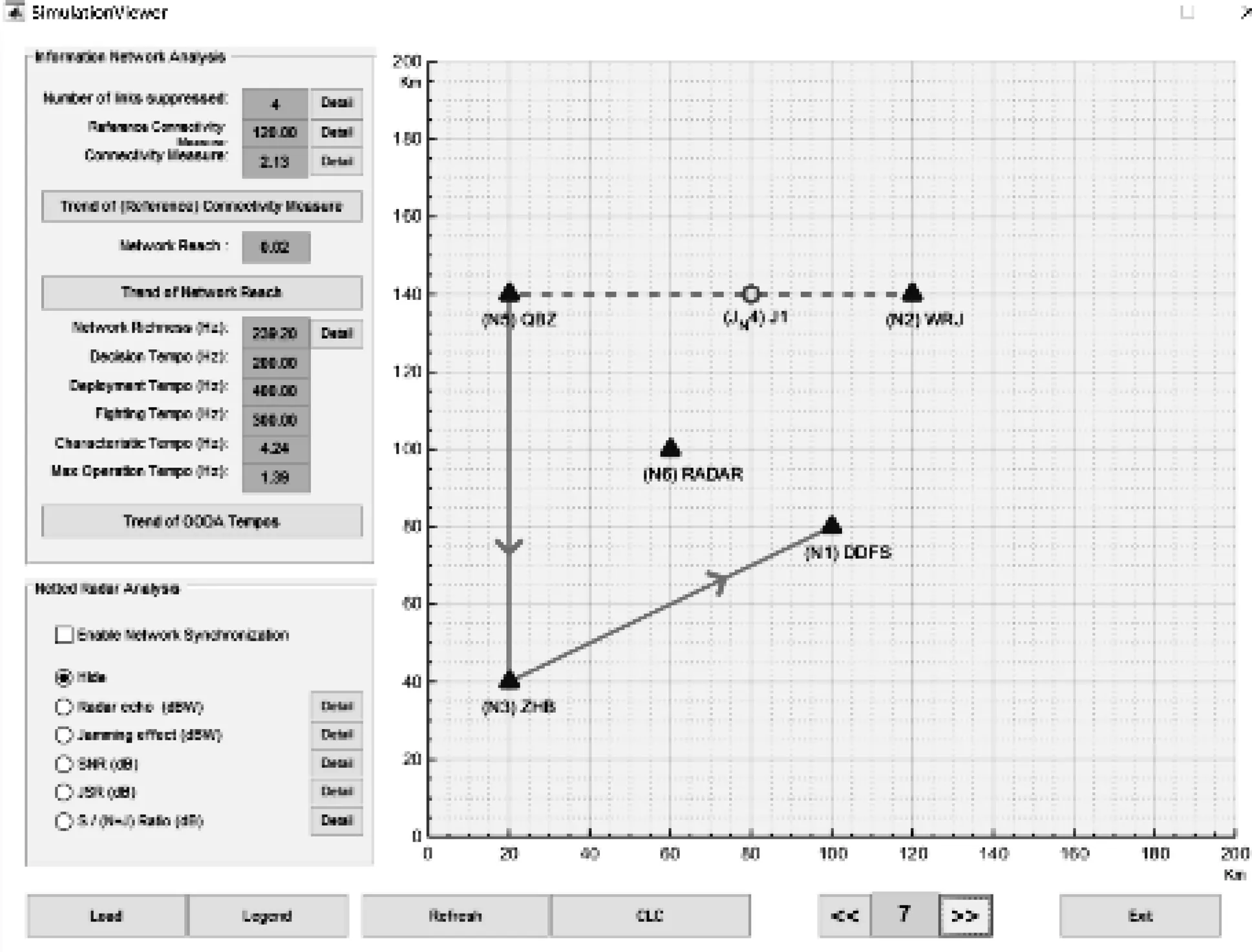
图8 在时序7的干扰仿真
为了度量我方作战体系遭受干扰前后网络内部的参数变化,以及由此而导致的OODA环路最大运行速度的变化趋势,表2给出了通过LPIsimNet计算得出的仿真结果。
从表2可以看出,随着干扰程度的加深,作战网络内部度量参数值(CM,IR,λT)呈现递减趋势,OODA环路最大运行速度ΛOODA也呈递减趋势。在ΛOODA计算公式中,假设决策速度、部署速度、作战速度都是已知且不变的,ΛOODA的值只受λT的限制。在这里λT是递减的,从公式也可以推导出ΛOODA是递减的,即通过仿真实验验证了理论推导的正确性。

表2 通过LPIsimNet计算得到的度量参数
5 结束语
本文的仿真实验是基于MATLAB软件程序集LPIsimNet,通过构建简易网络作战体系模型,从一定程度上评估了电子攻击对作战网络的影响效能,并评估了对应用在作战网络中的OODA环路的影响效能,得出的结论与之前的理论分析是相吻合的。由于在仿真计算OODA环路最大运行速度时只考虑了受传感器网络内部度量参数的影响,因而导致了仿真结果的局限性。
[1] Fusano A,Sato H,Namatame A. Muti-agent based combat simulation from OODA and network perspective[C]//Computer Modelling and Simulation(UKSim),2011 UKSim 13th International Conference on IEEE,2011:249-254.
[2] Phister,P W, Jr, CherryJ D.Command and control concepts within the network-centric operations construct[C]. Pro. of the IEEE Aerospace Conf.,2006: 1-9.
[3] 张明智,马力,季明.网络化体系对抗OODA指挥循环时测建模及实验[J].指挥与控制学报,2015,1(1):50-55.
[4] Posiel,R.Modern Communications Jamming Principles and Techniques,Artech House Inc.,2004.
[5] Ling M F,Moon T,Kruzins E D.Proposed network centric warfare metrics:From connectivity to the OODA cycle[J].Military Operations Research,2005,10(1):5-13.
[6] Chen Y Q.Simulation of network-enabled clectronic warfare metrics to assess the value of networking in a general information and radar topology[D].Monterey,CA:Naval Postgraduate School,2007:156.
[7] Garstka J J,Alberts D S.Network centric operation conceptual framework version 2.0[R]. Vienna,VA:Evidence Based Research,Inc.,2004:95.
Calculation and simulation of maximum action speed of OODA loop for networked combined combat systems
XU Kang, LI Hua-jun, WANG Sheng-chao, SHEN Zhi-li
(Unit 94005 of the PLA, Jiuquan 733306, China)
The OODA loop as an important military behavior has been embedded into all levels of the network operations. In order to measure the maximum action speed (ΛOODA) of the OODA loop, the networked combat systems model is built firstly, and the calculation method of the information exchange rate of the network-based combat systems is given. The measurement method of the maximum action speed of the OODA loop is further obtained through quantifying the time consumption of each stage of the OODA loop. Finally, the effects of the cyber attacks on the networked combat systems are simulated and calculated via the MATLAB software (LPIsimNet).
OODA loop; network; combined combat systems; information exchange rate
2017-05-05
徐康(1987-),男,助理工程师,硕士,研究方向:雷达装备作战运用及效能评估;李华军(1978-),男,工程师,本科,研究方向:雷达装备作战运用及效能评估;王盛超(1986-),男,工程师,硕士,研究方向:雷达装备作战运用及效能评估;申智利(1987-),男,助理工程师,硕士,研究方向:雷达装备作战运用及效能评估。
TP393
A
1009-0401(2017)02-0013-05

