被动测向最小二乘滤波法误差分析

任雪峰,李 强,陆 翔,付 林,涂刚毅

(1.海军驻南京地区雷达系统军事代表室，南京 210003；2.中国船舶重工集团公司第七二四研究所,南京211153)

被动测向最小二乘滤波法误差分析

任雪峰1,李 强2,陆 翔2,付 林2,涂刚毅2

(1.海军驻南京地区雷达系统军事代表室，南京 210003；2.中国船舶重工集团公司第七二四研究所,南京211153)

针对基于最小二乘法的测向误差滤波模型进行推导,给出滤波步长与测向误差的解析关系,并通过数值仿真验证其正确性。该结论对测向误差进行评估,并可直接应用于测向误差滤波,对单次测向结果进行修正。

被动测向;最小二乘法;滤波步长;测向误差

0 引 言

探测日益复杂的无线电信号并对其辐射源进行测向在军事和民用领域中有着非常重要的作用。[1]传感器通过接收信号源所发射的信号来捕获其方位信息。测向误差将影响定位精度。较大的误差可导致虚假测向交汇点的出现。[2-3]为解决该问题,最常见滤波算法为最小二乘测向角滤波[4]。最小二乘测向滤波误差分析具有极其重要的作用。已有Gauss-Markov定理表明,观测信号模型各误差分量方差相同且不相关[5-6],最小二乘估计在方差最小意义上最佳,可以达到CRLB下界[7]。

近年来,用蒙特-卡洛法对最小二乘测向滤波进行误差评估得到快速的普及。理论上,蒙特-卡洛法的实验次数越多,所得到的结果就越精确。基于蒙特-卡洛方法实验过程复杂、费时费力的特点,本文提出了一种更为简单、更为直观的误差解析方法。该方法给出了滤波步长对解析结果的影响,其分析给出的滤波解析结论不仅可用于评估最小二乘测向滤波误差,亦可为测向滤波误差评估提供理论下界。[9-10]

1 测向角最小二乘滤波方法

测向角观测值可由起始方位角、方位角的变化率表示[8]:

(1)

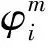
(2)

(3)

2 测向角最小二乘滤波误差分析

由最小二乘测向角滤波的模型可知,该滤波方法采用滑窗技术[7],通过多次测量使变量的估计误差平方和达到最小,提升测向跟踪稳定性。对于窗长为N的滑动窗,由式(1)可知第tN时刻输出滤角值为

(4)

展开后可得

(5)

其中,ti、tj、tN表示进行第i、j、N次测量的观测时刻。设时间间隔为△T,则ti=i·△T,tj=j·△T,tN=N·△T,公式(5)可化为

(6)

由于φi相互独立且服从N(ui,σi),因此

(7)

将上式按照j的次方项整理可得

(8)

其中

(9)

(10)

(11)

(12)

(13)

设若观测过程中传感器测角精度稳定,即观测角测向均方差σj=σ,则有

(14)

3 仿真分析

本文通过对比数值仿真结果与解析推导结果,设计两组对照试验,验证最小二乘滤波对测向误差影响的解析结论的正确性。

实验1 通过数值仿真生成含观测误差的测向角度,采用最小二乘滤波模型对测向角进行滤波,对结果进行方差统计分析。具体实施步骤如下:

(1) 在第i次试验中随机生成M次对目标观测的原始角度;

(2) 将原始角度送入滤波器;

(3) 选取滤波后第M个值并记录;

(4) 进行第i+1次试验;

(5) 计算N个样本值的方差,记录为滤波后的测向角方差。具体实施步骤如图1所示。

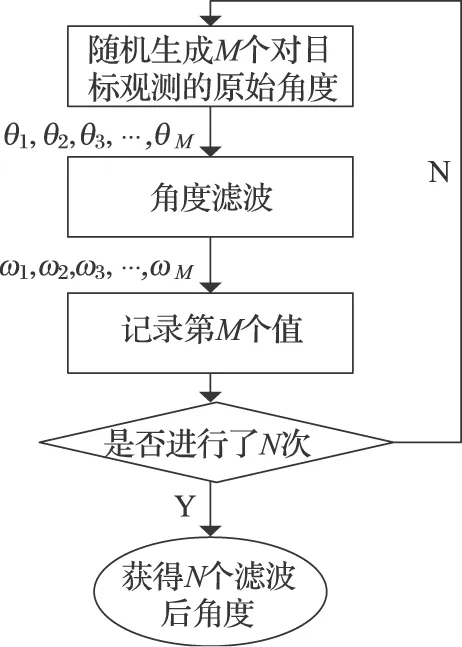
图1 蒙特-卡洛数值仿真实施步骤

实验2 根据预设测向角误差参数,采用本文推导出的解析表达式直接估算最小二乘测向滤波后的方差。具体实施步骤如下:

(1) 输入观测角测向均方差;

(2) 根据式(14)计算滤波后的测向角方差。

试验1、试验2的对照试验结果参见图2。图2给出数值仿真法及解析推导评估获得的滤波步长与输出角度方差的关系曲线。图中,待滤波的输入角度测向方差分别为0.6°、0.8°、1.0°。

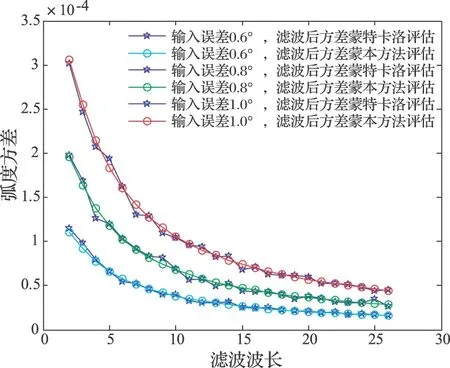
图2 角度最小二乘滤波处理后测向角方差与滤波步长的关系

由相关系数法分别计算上述3组曲线的相似度,得出结果为0.9977、0.9958、0.9974。由此可知,本文方法的解析分析结果能够很好地拟合数值仿真的结果,验证了解析分析的正确性。

4 结束语

本文给出最小二乘测向滤波条件下测向误差与滤波步长关系的解析表达,并通过与数值仿真结果对比验证其正确性。该方法解决了最小二乘滤波算法的误差评估,即可以直接通过解析式代入步长获得相应的评估误差。该方法简化了评估被动测向时滤波的角度误差,并为后续的定位误差校正提供理论基础,具有工程实践意义。

[1] 胡来招.雷达侦察接收机设计[M].北京:国防工业出版社,2000.1.

[2]DogancayK.Bearings-onlytargetlocalizationusingtotalleastsquares[J].SignalProcessing,2005,85(9):1695-1710.

[3]DogancayK.RelationshipbetweengeometrictranslationsandTLSestimationbiasinbearings-onlytargetlocalization[J].IEEETrans.onSignalProcessing, 2008,56(3):1005-1017.

[4]ZhangF,XuW,LiuX.OverviewofnonlinearBayesianfilteringalgorithm[C].ProcediaEngineering,2011,15:489-495.

[5]SheldonAxler.LinearAlgebraDoneRight[M]. 3rded.Springer,2015.

[6]RossSM.StochasticProcesses[M].JohnWiley,1983.

[7] 杨绿溪.现代数字信号处理[M]. 北京:科学出版社,2007.

[8] 茅玉龙,翟丽霞,黄鹤.无源雷达协同定位精度仿真研究[J].雷达与对抗,2000(4):22-26.

[9]NardoneSC,LindgrenAG,GongKF.Fundamentalpropertiesandperformanceofconventionalbearings-onlytargetmotionanalysis[J].IEEETrans.onAutomControl,1984,29(9):775-787.

[10] Gavish M, Weiss A J. Performance analysis of bearing-only target location algorithms[J]. IEEE Trans. on Aerosp.Electron.Syst,1992,28(93):817-828.

Error analysis of passive direction finding based on least square filtering method

REN Xue-feng1, LI Qiang2, LU Xiang2, FU Lin2, TU Gang-yi2

(1.Military Representatives Office of Radar System of the PLA Navy in Nanjing, Nanjing 210003; 2.No. 724 Research Institute of CSIC, Nanjing 211153)

The direction-finding error filtering model is deduced based on the least square method, and the analytical relationship between the filtering step and the direction-finding error is given. The correctness of the results is verified through the numerical simulation. The conclusions provide the theoretical basis for the evaluation of direction-finding error and can be directly applied to the direction-finding error filtering for single direction-finding result correction.

passive direction finding; least square method; filtering step; direction-finding error

2017-03-27;

2017-04-06

任雪峰(1986-)，男，工程师，研究方向：质量管理；李强(1990-),男,助理工程师,硕士,研究方向:雷达总体;陆翔(1988-),男,工程师,硕士,研究方向:雷达总体;付林(1975-),男,研究员,博士,研究方向:雷达总体;涂刚毅(1982-),男,高级工程师,博士,研究方向:雷达总体。

TN95

A

1009-0401(2017)02-0010-03