关于等物质的量规则的形成与探讨

李启华，余 锦，徐 涛，李利军

(兵器工业西南地区理化检测中心，重庆401120)

关于等物质的量规则的形成与探讨

李启华，余 锦，徐 涛，李利军

(兵器工业西南地区理化检测中心，重庆401120)

1985年赵梦月等首先提出了等物质的量规则［1］。等物质的量反应规则的内容详解及举例，参见文献［2］。它受到化学界的广泛重视、热烈讨论和积极思考，已被不少作者采用［1，3-5］。同时，在国家标准的起草中，也得到了充分运用［6-7］。广大的化学工作者也经常使用等物质的量规则，进行相关的专业教学、学生试验、溶液配制与计算、日常化学检测、仲裁分析和科研开发等活动。

等物质的量规则在化学分析领域得到了广泛运用，也有相应的多种叙述［1-3，5］。然而，其简单、适用、具体、规范、准确描述，至今未见详细报道。如冶金产品化学分析基础术语及分析化学术语中［8-9］，未见其定义;普通高中课程标准实验教科书《化学》(必修1)［10］和《分析化学导教·导学·导考》［11］中，也没见等物质的量规则的概念。物质的量在化学方程式计算中的应用，仅仅叙述为:化学方程式中各物质的化学计量数之比等于各物质的物质的量之比。

本课题组一直致力于化学分析基础技术及理论的研究、改进和提高，在实践中发现一些不足，特别是等物质的量规则，现提出几个有待改进的问题进行探讨。

1 等物质的量规则的形成

文献［2］中提出了等物质的量反应规则(本文称为赵氏表达法):

反应1:a A+b B→c C+d D

反应2:c C+t T→g G+h H

其中，A为被测定物质;T为标准溶液(滴定剂)。为了使被测物质A与滴定剂T建立联系，将反应1与反应2相加，则得:

反应3:a A+b B+t T→d D+g G+h H

如果把a A、b B、t T、d D、g G、h H这些特定组合作为基本单元，那么就能够说在反应3中1 mol a A和1 mol t T、1 mol b B反应生成1 mol d D、1 mol g G和1 mol h H。也就是说，这样选取基本单元的方法，使得反应在任何时刻所消耗的每种反应物与所产生的每种生成物的物质的量都相等。这就是等物质的量反应规则。

假定在滴定时所用标准溶液的浓度为c(t T)，所消耗的标准溶液体积为V(T)，那么参加反应的标准物质的物质的量见公式(1):

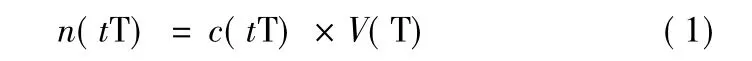
溶液中被测物质的物质的量见公式(2):

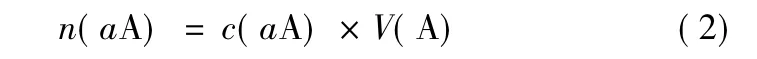
根据等物质的量反应规则，可得公式(3):

假定被测物质的浓度c1，体积为V1，标准溶液浓度为c2，所消耗的标准溶液体积为V2，那么公式(3)就变为公式(4):

公式(3)及公式(4)可称为等物质的量反应规则表达式。

随着时间的推移，以及相关化学工作者的广泛关注，逐渐形成了目前的“等物质的量规则”或“等物质的量定律［3］”。现人们习惯使用“等物质的量规则”称谓。

2 等物质的量规则的准确描述

试验中根据作者数年的分析化学专业教学并结合化学检测的实践经验，对等物质的量规则进行了潜心研究、总结和提炼，特别地提出了比较简单、适用、具体、规范、准确描述的“等物质的量规则”，称为李氏描述法。内容如下:

等物质的量规则是指在化学反应中，消耗的各反应物或/和产生的各生成物，对应基本单元的物质的量相等。

换句话说，等物质的量规则是指化学反应:

a A+b B+…=e E+f F+g G+…

数学表达式:

式中:a、b、e、f、g为简化的化学计量数;A、B、E、F、G为物质。

以典型氧化还原反应举例如下:

1)按初、中级基础教学配平的化学反应:

①解释“或”

各反应物分别为KMnO4、H2C2O4、H2SO4;对应基本单元分别为2KMnO4、5H2C2O4、3H2SO4;消耗的物质的量分别为Δn(2KMnO4)、Δn(5H2C2O4)、Δn (3H2SO4)。那么推出:Δn(2KMnO4)=Δn (5H2C2O4)=Δn(3H2SO4)。各生成物分别为Mn-SO4、CO2、K2SO4、H2O;对应基本单元分别为2MnSO4、10CO2、K2SO4、8H2O;生成的物质的量分别为Δn(2MnSO4)、Δn(10CO2)、Δn(K2SO4)、

Δn(8H2O)。那么，Δn(2MnSO4)=Δn(10CO2)= Δn(K2SO4)=Δn(8H2O)。

②解释“和”

Δn(2KMnO4)=Δn(5H2C2O4)=Δn(3H2SO4) =Δn(2MnSO4)=Δn(10CO2)=Δn(K2SO4)= Δn(8H2O)

2)按化学检测的反应

对于有1个及以上“非1”的化学计量数的化学反应，按物质之间实际参加反应的性质及关系，并遵守基本单元的合理、简单选择原则，同时又兼顾运用惯例，则有:

①解释“或”

3 等物质的量规则使用注意事项

1)化学反应按化学计量关系进行，即化学反应方程式要配平或平衡。

2)“消耗”针对参与反应的各反应物的各自的总加入量与各自的余量之差。

3)“产生”针对化学反应后，各生成物各自的生成量。

4)“或”，要么是指各反应物，要么是指各生成物。

5)“和”是指反应物与生成物之间关系。

7)“基本单元”，要求正确选择。

8)“相等”针对物质的量，且指任何反应时刻，不特指达到化学计量点时。

9)a A+b B+…=e E+f F+g G+…为通用化学反应方程式，既包含一种及多种反应物，同时也包含生成一种及多种生成物。

10)Δn(a A)=Δn(b B)=Δn(e E)=Δn(f F)=Δn(g G)=Δn(…)中，可根据需要选择两者或多者进行计算。

11)式中的a、b、e、f、g为简化的化学计量数，可以是整数，也可以是简分数，以方便计算;国家标准规定的化学计量数符号为。

对于上述的探讨，希望对国内同行能起到借鉴作用。同时，建议将准确描述的“等物质的量规则”，作为以后有关化学分析方法标准或术语标准的起草内容之一纳入其中。

［1］刘珍.化验员读本［M］.4版.北京:化学工业出版社，2004.

［2］赵梦月.SI在分析化学中的应用——当量的废除与等物质的量反应规则［J］.化学通报，1986(5):58－61.

［3］王令今，王桂花.分析化学计算基础［M］.2版.北京:化学工业出版社，2002.

［4］陈必友，李启华.工厂分析化验手册［M］.2版.北京:化学工业出版社，2009.

［5］张铁垣，杨彤.化验工作实用手册［M］.2版.北京:化学工业出版社，2008.

［6］GB/T 601-2002化学试剂标准滴定溶液的制备［S］.

［7］GB/T 20001.4-2015标准编写规则第4部分:试验方法标准［S］.

［8］GB/T 17433-2014冶金产品化学分析基础术语［S］.

［9］GB/T 14666-2003分析化学术语［S］.

［10］人民教育出版社，课程教材研究所，化学课程教材研究开发中心.化学(必修1)［M］.北京:人民教育出版社，2007.

［11］吴婉娥，张淑娟，张剑，等.分析化学导教·导学·导考［M］.5版.西安:西北工业大学出版社，2014.

［12］GB 3102.8-1993物理化学和分子物理学的量和单位［S］.

O65

B

1001-4020(2017)05-0552-03

10.11973/lhjy-hx201705012

2016-06-15