基于螺旋型耳蜗的数值分析

陈懿强， 姚文娟

(上海大学 土木工程系，上海 200444)

基于螺旋型耳蜗的数值分析

陈懿强， 姚文娟

(上海大学 土木工程系，上海 200444)

利用Patran建立包括前庭阶、鼓阶、基底膜、圆窗、卵圆窗在内的三维空间螺旋耳蜗模型。结合Nastran对基底膜进行频率响应分析，得到基底膜位移响应与耳蜗内压力(包括前庭阶与鼓阶处的压力)，计算结果与相关实验吻合，验证了模型的正确性。基于空间螺旋模型研究了流体黏度对于耳蜗阻抗的影响以及正向、逆向激励对于基底膜12 mm处沿横向位移幅值的影响。结果表明，由于流体黏度的存在增大了耳蜗的阻抗。同时，当频率较高时，在正，逆不同激励作用下，相对于简化的直腔耳蜗模型，螺旋基底膜的曲率对基底膜沿横向的幅值影响较大，从侧面反应出螺旋耳蜗结构本身的曲率对基底膜感音域的扩大作用。

螺旋耳蜗；耳蜗阻抗；逆向激励；流体黏度；基底膜曲率

人的听觉系统主要由外耳道、中耳与内耳组成。声音以声波方式传入外耳道并引起鼓膜振动，鼓膜的振动经听骨链传至镫骨底板，通过卵圆窗对耳蜗中的淋巴液施加激励，使得耳蜗中的基底膜因两侧淋巴液压力不同而发生垂直方向上的振动，最后由基底膜上的毛细胞和神经纤维将基底膜的振动转化为神经冲动并将神经信号传至大脑听中枢而产生听觉。

最早研究耳基底膜宏观运动并以此获得诺贝尔奖的Békésy[1]，通过对动物耳蜗的实验，发现耳蜗内沿基底膜底部向顶部传播的行波。Hillery[2]从神经生理学的角度验证了内耳中行波的存在，为运用力学原理分析基底膜的振动特性奠定了基础。

在哺乳动物耳蜗生理学体系中，行波是一种特殊的压力波。而压力波是由镫骨振动在耳蜗的淋巴液中产生的。Nature报道了测量耳蜗内压力波的直接测量法，揭示了耳蜗内压力波的组成[3]。同时，Olson等[4-5]还进一步发明了测量耳蜗内压力的微观压力感应法，对动物的基底膜速度幅值、螺旋器周围的压差进行了研究。在此基础上，Nakajima等[6]采用同样的方法得到了人耳蜗内压力、压力差。

在正向激励下的耳蜗阻抗是耳蜗重要的特性参数。Zwislocki[7]最早提出了耳蜗阻抗的概念，之后由Merchant等[8]，Puria 等[9]，Aibara 等[10]和Nakajima等先后通过实验得到了人耳蜗的阻抗，为进一步研究人内耳的感音特性提供了实验依据。此外，田佳彬等[11]在近期的研究中发现黏弹性本构对于人耳动力学特性也存在影响，尤其在高频段提升较明显，与实验测量数据匹配效果更好。

为了深入研究耳蜗的感音过程，很多学者对基底膜振动特性的参数进行了研究。早期，Johnstone等[12-13]采用Mossbauer技术和容量探测技术分别对豚鼠和猫进行实验，测得了相应基底膜的振动幅值。之后，Gundersen等[14]则采用Mossbauer技术得到了人耳基底膜的振动特性。Mammano[15]通过使用激光迈克尔逊干涉仪测量了逆向激励下耳蜗的运动特性，发现耳蜗的放大与外毛细胞的性质有关。

随着关于耳蜗的实验不断丰富，促进了学者从理论的角度建立数学模型开展研究。早期，主要基于简化的直腔耳蜗，应用格林函数法、有限差分、WKB等方法逐步建立了二维到三维的数学模型[16-19]。Parthasarathi等[20]建立三维数值模型采用伽辽金法预测了耳蜗的响应，同时发现特征频率附近基底膜的速度受到流体的影响。之后，Matin等[21]与Ni等[22]分别研究了基底膜沿宽度的振动形态和模态变化，Ma等[23]则进一步建立了三维螺旋的数学模型，研究了螺旋结构对于基底膜振动的影响，逐步把基底膜从简化的拉直模型发展到复杂的螺旋型结构。

由于耳蜗结构的复杂性，建立耳蜗的数学模型时存在很多简化，为了更好的研究耳蜗的感音过程，基于有限元软件的数值模拟被很多学者采用。Skrodzka[24]建立了主动与被动的三维基底膜模型，得到了相应参数的输入-输出函数曲线，通过研究发现基底膜的损伤会影响大部分函数曲线的变化。但就当前普遍采用的宏观耳蜗模型而言，主要建立简化的直腔耳蜗模型模拟基底膜运动[25-28]。Zhang等[29]在植入式助听器的研究中虽建立了螺旋型耳蜗模型，但主要检验了中耳和内耳的传输功能，对于螺旋型耳蜗的优势没有进一步的分析。

同时，学者们通过对于耳蜗不同角度的研究，验证了人耳基底膜上一种特殊压力波——行波的存在，得到了人耳基底膜的振动特性、耳蜗的阻抗特征，并基于有限元软件模拟了基底膜的运动特性。但以往的数值模拟中没有涉及流体的黏度对于耳蜗阻抗的影响，没有进一步研究螺旋结构的曲率对于基底膜运动以及耳蜗内压力的影响。

鉴于此，本文建立了吻合实际人耳的三维螺旋型耳蜗模型，考虑了淋巴液与周围结构的流固耦合作用，研究了耳蜗在正向激励作用下，流体黏度对于耳蜗阻抗的影响。同时，对比分析了在正向、逆向激励下，对于耳蜗内压力的变化情况以及对于基底膜12 mm处横向幅值的影响。

1 耳蜗模型的建立

1.1 螺旋耳蜗的有限元模型建立

基于人体正常右耳的CT扫描图像以及相关文献[30-31]，通过PATRAN软件建立三维螺旋的空间耳蜗模型。螺旋状内耳有2.5周，内耳中的空间被前庭膜和基底膜分成三个腔：前庭阶，蜗管和鼓阶，并且充满了淋巴液(见图1)。前庭阶，蜗管和鼓阶的横截面面积之比大致为：5:3:8。基底膜长度为34.86 mm，基底膜在厚度与宽度上的尺寸线性变化，顶端和底端的厚度分别为7.5 μm和2.5 μm(见图2)，顶端和底端的宽度分别为0.1 mm与0.5 mm。本文建立的耳蜗模型没有考虑柯蒂氏器的作用，即没有考虑耳蜗的主动机制，为被动模型。最后利用NASTRAN软件进行三维流-固耦合动力学分析。

(a) 耳蜗有限元模型

(b) 耳蜗有限模型图1 耳蜗的网格划分模型Fig.1 The mesh of cochlea

图2 螺旋基底膜的有限元模型图Fig.2 The finite element model of spiral basilar membrane

运用Patran将模型进行网格划分。鼓阶：7 878个节点，6 200个八节点六面体(Hex8)Fluid单元。前庭阶：3 131个节点，1 900个八节点六面体(Hex8)Fluid单元。蜗管：7 878个节点，6 400个八节点六面体(Hex8)Fluid单元。蜗孔：990个节点，725个八节点六面体(Hex8)Fluid单元。卵圆窗(前庭窗)：98个节点，83个四节点四边形(Quad4)2D-Membrane单元。圆窗(蜗窗)：78个节点，62个四节点四边形(Quad4)2D-Membrane单元。基底膜：303个节点，400个四节点四边形(Quad4)2D-Membrane单元。骨质螺旋板：808个节点，600个四节点四边形(Quad4)2D-Membrane单元。前庭膜：1 111个节点，1 000个四节点四边形(Quad4)2D-Membrane单元。耳蜗各结构网格如图1(a)所示。

1.2 材料参数

耳蜗模型中的结构材料属性包括卵圆窗、圆窗、基底膜、前庭膜与骨质螺旋板的密度和弹性模量，如表1所示[32]。基底膜的弹性模量沿着基底膜长度方向变化，在本研究中，基底膜的弹性模量由底部的50 MPa 线性地减小顶端的3 MPa。淋巴液的属性，如表2所示。

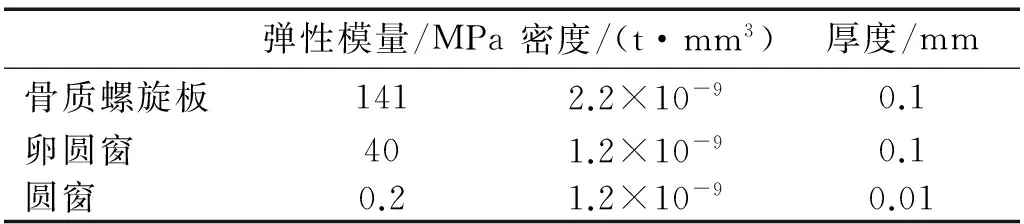
表1 耳蜗模型中的结构材料属性

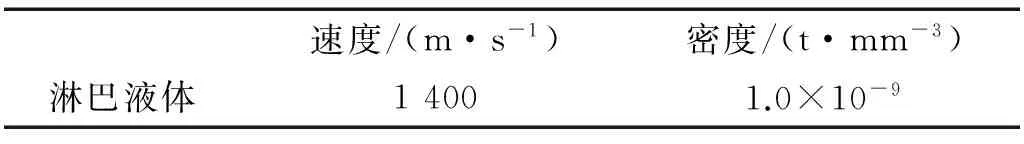
表2 耳蜗模型中的淋巴液属性

1.3 边界条件

(1)卵圆窗上施加106.4 dB激励，模拟纯音声压刺激 (100～10 000 Hz)。

(2)圆窗与卵圆窗外边缘视为固定约束。

(3)基底膜、前庭膜为流固耦合界面。

1.4 流固耦合动力学方程

在流体与结构耦合计算中，流体与结构相互作用，耦合动力学基本方程可表示为

(1)

其中：

[Mfs]=ρ0[Re]T

(2)

[Kfs]=-[Re]

(3)

式中：[M]为结构质量矩阵；[Mfs]为耦合面上的质量矩阵；[Mp]为流体质量矩阵；[C]为结构阻尼矩阵；[Cp]为流体阻尼矩阵；[Kp]为流体刚度矩阵；{u}为位移矢量；p为声压矩阵。

1.5 接触面基本方程

假设单元为无厚度的：

(4)

式中：Ks为切向刚度;Kn为法向刚度;x、y和n是实际接触面两个坐标方向及单元的法线方向;Δu、Δv和Δw为接触面单元上盘与下盘切向方向的相对位移和法向方向的相对位移，即

(5)

其中[B]=[B1B2B3B4B5B6B7B8]

(6)

{δ}=[u1v1w1……u8v8w8]T

(7)

(8)

2 计算结果

2.1 耳蜗的阻抗

图3中显示了模型计算所得的耳蜗阻抗(卵圆窗附近前庭阶流体压力与体速度的比值)并与Merchant等的实验数据进行对比。从图中可知，模型所得结果与实验数据在高频有较好的一致性，其中与Puria等的实验数据最为接近。同时从图中可以看出阻抗在3 000～10 000 Hz间逐渐增大，在3 000取得较小值20 GΩ。

图 3 耳蜗的阻抗Fig.3 Cochlear input impedance magnitude

2.2 中耳的增益

Puria等、Aibara等、Nakajima等分别通过测量新鲜人耳颞骨中外耳道声压和前庭阶声压的差值，得到了中耳的声压增益曲线，如图4所示。

由图4可知，在各个频率段，声压增益在1 kHz附近增加最大，大约为20 dB，在其他频率段有所降低。用Mathematica软件对三组曲线进行拟合，得到中耳声压增益拟合曲线，绘于图4中，通过Mathematica得到拟合式(9)(相关系数R=0.919)。

(9)

式中：x为频率；y为中耳声压的增益。

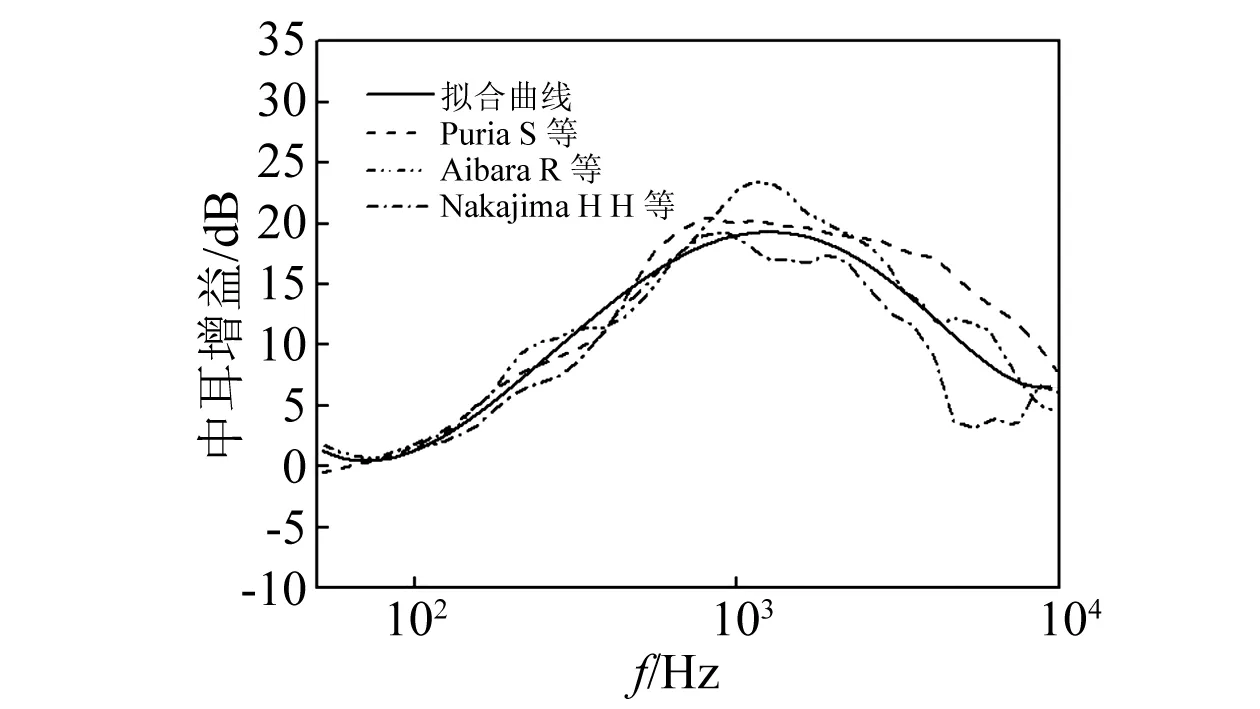
图4 中耳的增益Fig.4 Middle ear gain of the human ear

根据Gundersen等[33]、Stenfelt等[34]的实验数据以及Kim等[35]的模拟数据如图5(a)所示，距底部12 mm处基底膜的特征频率约为2.1 kHz～3.6 kHz,,取平均值2.8 kHz。由式(9)计算得，当频率为2.8 kHz时，中耳声压增益约为16.4 dB，之后将中耳声压增益调整施加在卵圆窗上的声压。

2.3 基底膜的响应

图5(a)中显示了当卵圆窗上施加106.4 dB激励时(此激励的作用效果根据式(9)以及2.2节引文所述相当于在外耳道上施加90 dB激励的效果)，模型模拟得到了基底膜上距底端12 mm处的基底膜幅值与镫骨底板幅值(取卵圆窗中心点)之比随频率变化的关系。同时图5(a)中还给出了Gundersen等[33]、Stenfelt等[34]的实验数据以及Kim[35]等的有限元模拟曲线，从图中曲线可知，Gundersen实验的特征频率为3 500 Hz，Kim等的有限元模拟结果与其相似。而本文的特征频率为2 500 Hz，与Stenfelt的实验结果相似，因此本文的模拟结果与实验结果有很好的一致性。图5(b)则反映出本模型模拟的相位数据与实验数据的对比，从图中可知在经过特征频率后，曲线趋势下降明显。

2.4 耳蜗的映射

图6显示了基底膜沿耳蜗纵向，在各频率上响应峰值的位置。方块实心表示本文模型计算所得曲线，长虚线为 Greenwood等[36]的模型计算所得曲线，短虚线为Békésy实验测量获得的低频段的曲线。通过对比分析，可见本模型的结果与实验比较接近。同时也能看出，对应于不同的频率，在基底膜上沿纵向达到峰值所对应的位置不同，反应了基底膜的频率选择特性。

2.5 正向激励传递函数与逆向激励传递函数

耳蜗内压分别取值卵圆窗和圆窗附近的压力，PEC取相当于外耳道90 dB的声压。通过与Nakajima实验数据的对比，正向激励下前庭阶传递函数(PSV/PEC)与鼓阶的传递函数(PST/PEC)分别绘于图7和8中。由图7可知，在600～4 000 Hz时曲线趋于平稳，模型所得前庭阶压力值大致比试验数据小10～15 dB，与实验数据在趋势上有一定相似。由图8可知，在200～2 000 Hz时，模型所得数据比试验数据高，在6 000 Hz后曲线趋于平稳。总体趋势与实验数据相似。图9表示了逆向激励下(即PRW为在圆窗90 dB的激励)的传递函数(PST/PRW)，并与Nakajima实验数据的对比，在200～400 Hz曲线逐步上升，在400～1 000 Hz趋于平稳，但比实验值大5～10 dB，当大于3 000 Hz后曲线再次趋于平稳。

(a) 12 mm处基底膜与镫骨底板幅值之比

(b) 相位图5 有限元模型数据与实验数据的对比Fig.5 Comparison between the data from the model and that from the experiment

图6 基底膜的频率-位点图Fig.6 Simulated cochlear map compared with the experimental data

图7 正向激励时传递函数并与实验数据的对比Fig.7 Model-derived cochlear fluid pressure magnitude in dB (PSV/PEC),in comparison with the experimental data

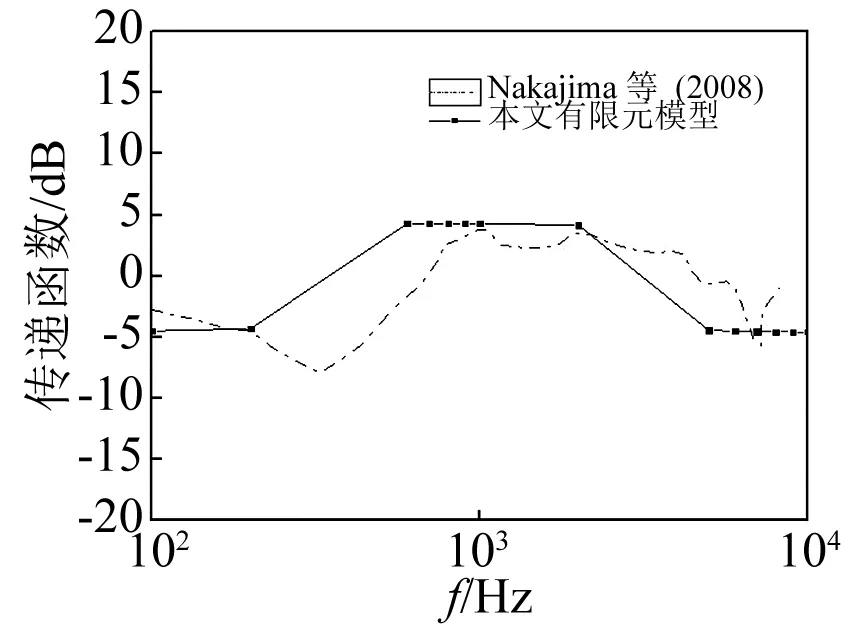
图8 正向激励时传递函数并与实验数据的对比Fig.8 Model-derived cochlear fluid pressure magnitude in dB (PST/PEC), in comparison with the experimental data

图9 逆向激励时传递函数Fig.9 Magnitude of reverse pressure transfer function

2.6 流体黏度对于耳蜗阻抗的影响

流体黏度对于耳蜗阻抗的影响，见图10。图10显示了流体有黏度与没有黏度时，耳蜗阻抗随频率变化时的大小。从图中可知，在700～2 000 Hz时阻抗随频率逐渐增长，有黏度的曲线明显比无黏度曲线高，但相差不大，在3 000 Hz时其两者间相差最大为1 GΩ左右。

图10 黏度对于耳蜗阻抗的影响Fig.10 Effect of fluid viscosity to the cochlear impedance

2.7 正、逆向激励对于基底膜横向幅值的影响

相对于拉直基底膜上任一横截面上点的几何参数相同，螺旋基底膜上由于螺旋曲率的存在，其任一横截面上点的几何存在差异，因此为了研究正、逆向激励下，螺旋结构对于基底膜幅值的影响,在基底膜任意截面处半径最小的点设为1点为内半径，半径最大的点设为5点为外半径，如图11所示。

图11 螺旋基底膜局部放大Fig.11 Enlargement of spiral basilar membrane

图12中表示了正向激励下(即卵圆窗上加80 dB SPL声压)，基底膜距底端12 mm处横向各点幅值随频率变化趋势。图中纵轴为各点与1点的幅值之比。从图中可以看出，随着基底膜曲率的减小，基底膜横向各点偏离的趋势相同，但偏离程度逐渐增大，说明基底膜幅值随着基底膜曲率减小而逐渐变大，但在低频时偏离相对较小，在大致在2 500 Hz左右发生突变，与此处最佳频率相似，可见基底膜横向位移发生变化的转折点为此处基底膜的最佳频率，即当在距离基底膜底端12 mm处时，基底膜横向位移发生变化的转折点为2 500 Hz，与此处的特征频率相同。通过转折点后，在高频阶段各点幅值的偏离程度变大，说明随着基底膜曲率减小，基底膜振幅减小。

图12 正向激励时基底膜沿横向幅值对于1点的比值Fig.12 The amplitude of different position of BM at 12 mm in a transverse direction was normalized with respect to the amplitude of position of 1 under forward pressure

图13中表示在逆向激励下(即圆窗上加80 dB SPL声压)，螺旋基底膜曲率对于基底膜横向幅值的影响。图中纵轴为各点与1点的幅值之比。从图中可知，与1点幅值相比，除了2点的偏离趋势与正向激励时相似外，其余各点偏离趋势与正向激励时的趋势相反，可能是由于基底膜曲率较小时，正向、逆向不同激励对于基底膜横向幅值影响明显。同时，图中曲线的趋势在2 500 Hz左右发生突变，在低频时基底膜幅值随着基底膜曲率的减小而减小，在高频时，则相反。各点之间的偏离程度随着基底膜曲率的减小而减小。

图13 逆向激励时基底膜沿横向幅值对于1点的比值Fig.13 The amplitude of different position of BM at 12mm in a transverse direction was normalized with respect to the amplitude of position of 1 under reverse pressure

3 讨论与分析

文中图5(a)和(b)显示了在基底膜特定位置(距基底膜底端12 mm)处的位移，与Greenwood、Békésy等实验数据有较好的一致性。图6揭示了在正向激励(即激励施加于卵圆窗)时，基底膜沿纵向从底部到顶端位移的分布情况，从图中可知，基底膜的振幅的最大峰值点随频率的变化而变化，反应了基底膜沿纵向的频率选择特性。

耳蜗内压力取自于本模型的鼓阶与前庭阶底部处圆窗与卵圆窗附近的压力，正向激励时前庭阶与鼓阶的传递函数分别绘于图7，8。对比图7与图8可知，在300～1 000 Hz之间，PSV/PEC 数值比PST/PEC略高。同时，从图7中可知，与实验数据相比，模拟的数据有相似的趋势，在600～4 000 Hz内比试验数据小10～15 dB。正向激励时的传递函数在高频时，与实验数据相比有更好的一致性。逆向激励时鼓阶的传递函数绘于图9，在200～2 000 Hz间，模拟的数据比实验数据高3～5 dB，在高于2 000 Hz时，与实验数据更加接近。

图10中通过对比有无流体黏度，证明了流体的黏度会增大耳蜗的阻抗，其原因可能是由于声波在流体中传递时流体间的黏度消耗了更多的能量，与无黏度的流体相比其两者的整体趋势相近，在低频时相差不大，在高频时差异较明显。可见当采用螺旋型基底膜时，在较高的频率下，流体黏度对于耳蜗的阻抗的影响较大。

由图12可知，在正向激励下沿基底膜横向各点的位移变化趋势是相似的，在低于2 500 Hz时，螺旋基底膜的曲率对于基底膜横向各点幅值的影响不大，在高于2 500 Hz时，螺旋基底膜的曲率对于基底膜横向各点幅值的影响明显，由于基底膜的位移幅值与频率间存在相关性，因此相对于简化的直腔耳蜗模型，螺旋耳蜗结构本身的曲率对基底膜感音域的扩大也起到了一定的作用。对比图12与图13可知，在正向激励下，基底膜横向各点幅值与1点幅值之比最大偏移量为0.1左右，在逆向激励下，基底膜横向各点幅值与1点幅值之比最大偏移量也为0.08左右。当基底膜曲率较小时，两者只有在偏移的方向上相反，可见当正向传导途径即听骨链到卵圆窗的途径被阻断时，可以通过在圆窗施加机械振动传导到耳蜗[37]，证明了逆向激励对于治疗混合性耳聋的可行性，也为其提供了一定的理论基础。

4 结 论

本文建立了吻合实际人内耳的空间螺旋型耳蜗模型，基于模型得到的基底膜位移响应、耳蜗的阻抗和耳蜗的映射，与实验数据相比有较好的一致性，验证了本文模型的正确性。同时，模拟得到的耳蜗内压力比值(PSV/PEC 和PST/PEC)趋势与实验数据一致。

通过对比有无流体黏度，发现流体黏度的存在增大了耳蜗的阻抗，同时，与无黏度的流体相比，在高频时耳蜗阻抗相差较大。

在正、逆不同激励作用下，基底膜横向各点的位移幅值随频率变化趋势相似，在高频时随基底膜曲率变化剧烈，基底膜横向位移发生突变时的频率为基底膜相应的最佳频率。因此，相对于简化的直腔耳蜗模型，螺旋耳蜗结构本身的曲率对基底膜感音域有扩大作用。同时，当基底膜曲率较小时，在正、逆不同激励作用下，沿基底膜横向幅值的振动方向相反。

本文所建立的三维螺旋型模型更加精确地描述了耳蜗在高频段的变化，为进一步研究人耳耳蜗提供了更加精确的数值计算平台。

[1] VON BÉKÉSY G. Experiments in Hearing. [M]. New York: McGraw-Hill Book Company Inc., 1960.

[2] HILLERY C M, NARINS P M. Neurophysiological evidence for a traveling wave in the amphibian inner ear[J]. Science, 1984, 225(4666):1037-1039.

[3] OLSON E S. Direct measurement of intra-cochlear pressure waves.[J]. Nature, 2000, 402(6761):526-529.

[4] OLSON E S. Observing middle and inner ear mechanics with novel intracochlear pressure sensors.[J]. Acoustical Society of America Journal, 1998, 103(6):3445-3463.

[5] OLSON E S. Intracochlear pressure measurements related to cochlear tuning.[J]. Journal of the Acoustical Society of America, 2001, 110(1):349-367.

[6] NAKAJIMA H H, DONG W, OLSON E S, et al. Differential intracochlear sound pressure measurements in normal human temporal bones[J]. Jaro Journal of the Association for Research in Otolaryngology, 2009, 10(1):23-36.

[7] ZWISLOCKI J J. The role of the external and middle ear in sound transmission[C]∥ Tower D B. The Nervous System, Vol 3, Human Communication and its Disorders. New York :Raven Press,1975.

[8] MERCHANT S N, RAVICZ M E, ROSOWSKI J J. Acoustic input impedance of the stapes and cochlea in human temporal bones[J]. Hearing Research, 1996, 97(1/2):30-45.

[9] PURIA S , PEAKE W T, ROSOWSKI J J. Sound-pressure measurements in the cochlear vestibule of human-cadaver ears[J] Journal of the Acoustical Society of America, 1997, 101(1):2754-2770.

[10] AIBARA R, WELSH J T, PURIA S, et al. Human middle-ear sound transfer function and cochlear input impedance.[J]. Hearing Research, 2001, 152(1/2):100-109.

[11] 田佳彬,饶柱石,塔娜,等.黏弹性本构对于人耳动力学特性影响的数值研究[J].振动与冲击,2015,34(22): 74-81. TIAN Jiabin, RAO Zhushi,TA Na, et al. Numerical analysis on the effects of viscoelastic constitutive relation on dynamic characteristics of human ear[J].Journal of Vibration and Shock, 2015,34(22):74-81.

[12] JOHNSTONE B M, BOYLE A J F. Basilar membrane vibration examined with the M ssbauer technique[J]. Science, 1967, 158(3799):389-390.

[13] KHANNA S M, LEONARD D G. Basilar membrane tuning in the cat cochlea.[J]. Science, 1982, 215(4530):305-306.

[14] GUNDERSEN T, SKARSTEIN O, SIKKELAND T. A Study of the vibration of the basilar membrane in human temporal bone preparations by the use of the mossbauer effect[J]. Acta Oto-laryngologica, 2009, 86(3/4):225-232.

[15] MAMMANO F , ASHMORE J F. Reverse transduction measured in the isolated cochlea by laser Michelson interferometry[J]. Nature, 1993, 365(6449):838-841.

[16] ALLEN J B. Two-dimensional cochlear fluid model: new results[J]. Journal of the Acoustical Society of America, 1977, 61(1):110-119.

[17] NEELY S T. Finite difference solution of a two-dimensional mathematical model of the cochlea[J]. Journal of the Acoustical Society of America, 1981, 69(5):1386-1393.

[18] PARTHASARATHI A A, GROSH K, NUTTALL A L. Three-dimensional numerical modeling for global cochlear dynamics[J]. Journal of the Acoustical Society of America, 2012, 107(1):474-485.

[19] LIM K M, STEELE C R. A three-dimensional nonlinear active cochlear model analyzed by the WKB-numeric method[J]. Hearing Research, 2002, 170(1/2):190-205.

[20] PARTHASARATHI A A, GROSH K, NUTTALL A L. Three-dimensional numerical modelling for global cochlear dynamics[J]. J Acoust Soc Am,2000,107(1):474-485.

[21] MARTIN H, ALAN C, GILES H, et al. Mathematical modeling of the radial profile of basilar membrane vibrations in the inner ear.[J]. Journal of the Acoustical Society of America, 2004, 116(2):1025-1034.

[22] NI G J, ELLIOTT S J. Effect of basilar membrane radial velocity profile on fluid coupling in the cochlea[J]. Journal of the Acoustical Society of America, 2013, 133(3):181-187.

[23] MA J W, YAO W J. Research on the distribution of pressure field on the basilar membrane in the passive spiral cochlea[J].J Mech Med Biol , 2014,14(4): 1450061.

[24] SKRODZKA E B. Modelling of some mechanical malfunctions of the human basilar membrane[J].Applied Acoustics,2005,66(9): 1007-1017.

[25] BOHNKE F, ARNOLD W. 3D-finite element model of the human cochlea including fluid-structure couplings[J]. ORL, 1999, 61(5):305-310.

[26] GAN R Z, REEVES B P, WANG X. Modeling of sound transmission from ear canal to cochlea[J]. Annals of Biomedical Engineering, 2007, 35(12):2180-2195.

[27] HU Y. Finite element modelling of human auditory periphery including a feed-forward amplification of the cochlea[J]. Computer Methods in Biomechanics & Biomedical Engineering, 2014, 17(10):1096.

[28] KIM N, HOMMA K, PURIA S. Inertial bone conduction: symmetric and anti-symmetric components[J]. Journal of the Association for Research in Otolaryngology, 2011, 12(3):261-279.

[29] ZHANG X, GAN R Z. A comprehensive model of human ear for analysis of implantable hearing devices[J]. IEEE Transactions on Bio-medical Engineering, 2011, 58(10):3024-3027.

[30] HALL J J W, MUELLER H G. Audiologist’s desk reference volume II: audiolologic management, rehabilitation and terminology[M].San Diego: Singular Publishing Group, 1998.

[31] MARC THORNE B S, SALT A N, MA D M, et al. Cochlear fluid space dimensions for six species derived from reconstructions of three-dimensional magnetic resonance images[J]. Laryngoscope, 1999, 109(109):1661-1668.

[32] WANG Z L. FEM simulation of sound transmission based on integrated model of middle ear and cochlea[J]. Chinese Journal of Biomedical Engineering, 2011, 30(1):60-66.

[33] GUNDERSEN T, SKARSTEIN O, SIKKELAND T. A study of the vibration of the basilar membrane in human temporal bone preparations by the use of the mossbauer effect[J]. Acta Oto-laryngologica, 2009, 86(3/4):225-232.

[34] STENFELT S, PURIA S, HATO N, et al. Basilar membrane and osseous spiral lamina motion in human cadavers with air and bone conduction stimuli[J]. Hearing Research, 2003, 181(1/2):131-143.

[35] KIM N, HOMMA K, PURIA S. Inertial bone conduction: symmetric and anti-symmetric components[J]. Journal of the Association for Research in Otolaryngology, 2011, 12(3):261-279.

[36] GREENWOOD D D. A cochlear frequency-position function for several species—29 years later.[J]. Acoustical Society of America Journal, 1990, 87(6):2592-2605.

[37] VITTORIO C, SOLI S D, MARCO C, et al. Treatment of mixed hearing losses via implantation of a vibratory transducer on the round window[J]. International Journal of Audiology, 2006, 45(10):600-608.

Numerical simulation on a spiral cochlear

CHEN Yiqiang, YAO Wenjuan

(Department of Civil Engineering, Shanghai University, Shanghai 200444, China)

A three-dimensional passive spiral cochlear model including the oval window (OW), round window (RW) and basilar membrane (BM) was established. The harmonic response analysis was then carried out. The results on the cochlear impedance, basilar membrane response and intracochlear pressures containing the scala vestibule and scala tympani pressure were obtained. The satisfactory agreements between the model results and the experimental data in the literature prove the validity of the finite element (FE) model. Based on the FE model, the effect of fluid viscosity on the cochlear impedance and the variation of amplitude of the BM in the transverse direction at a 12 mm distance under the normally forward sound stimulation and reverse RW stimulation was discussed. The results indicate that the cochlear impedance is increased because of the fluid viscosity. In the meantime, compared with the simplified uncoiled model, the curvature of the spiral BM has a great effect on the amplitude in the transverse direction at high frequencies under different stimulations and the sensitivity frequency range is expanded on account of the spiral geometrical characteristic.

spiral cochlear; cochlear impedance; reverse stimulation; fluid viscosity; curvature of the BM

国家自然科学基金(11272200；11572186)

2016-04-01 修改稿收到日期： 2016-06-06

陈懿强 男，博士生，1989年生

姚文娟 女，博士，教授，博士生导师，1957年生

O3；R76

A

10.13465/j.cnki.jvs.2017.14.007