桩-土水平弹簧系数对桥梁地震反应影响的参数分析

高 昊， 王君杰， 苏俊省， 宋彦臣

(同济大学 土木工程学院，上海 200092)

桩-土水平弹簧系数对桥梁地震反应影响的参数分析

高 昊， 王君杰， 苏俊省， 宋彦臣

(同济大学 土木工程学院，上海 200092)

集中参数法是目前土木工程抗震计算中考虑桩土地震相互作用的实用方法。从有限元方法的角度来看，集中参数方法将地层半无限空间模型化为一个无几何尺度的抽象的力学单元，这里称其为宏单元，其计算模型的选用和参数确定直接影响计算结果的精度。针对不同的地震动输入和工程中各种常见的土层，基于考虑土体非线性的Boulanger宏单元， m法和Mindlin解等三种桩—土水平弹簧模型，进行了详尽的参数分析工作，旨在说明对桥梁地震反应影响很大的桩-土水平弹簧系数的取值问题。

地震； 桩-土相互作用； 非线性； 宏单元

桩土地震相互作用是工程结构抗震理论中的一个重要课题，一直得到广泛的关注和研究。讨论的重点在两个方面：①桩-土地震相互作用的计算理论和方法；②是桩-土地震相互作用对桩基桥梁地震反应的主要影响因素和在工程设计中的实用考虑方法。

在桩-土地震相互作用的计算理论和方法方面，Penzien等[1]提出了集中参数模型(彭津模型)，用于解决软土地基上桩基础桥梁抗震分析计算问题，见图1。之后该模型得到[2-4]深入研究和讨论，并得到了广泛的工程应用，成为目前土木工程抗震计算中考虑桩土地震相互作用的实用方法。

图1 桩土地震相互作用的集中参数模型Fig.1 Concentration parameter model for seismic soil-pile interaction

彭津模型将土模型化为一系列弹簧，描述土的变形性质。采用这种模型，关键点有二：①描述弹簧的函数形式；②弹簧参数的确定方法。本文的目的是针对目前广泛使用的Boulanger等[5]、m法和明德林(Mindlin)[6]解答三种定义弹簧的方法，研究这些因素对桩基桥梁地震反应的影响规律。

1 桩土地震相互作用的集中参数模型

1.1 基本力学元件

建立土宏单元的基础是对桩土地震相互作用的机理的深入理解。从目前已有的研究成果来看，桩土地震相互作可以产生图2所示的几种力学现象[7]：①桩土界面相对滑动引起摩擦,见图2(a)；②桩土之间可能重复发生脱离-接触,见图2(b)；③桩的主动面和被动面受到土压力，土可能进入强的非线性状态,见图2(c)。桩土地震相互作用宏单元构造的第一步是针对上述力学特征构造出相应的力学元件。

图2 桩-土地震相互作用机理Fig.2 Soil-pile interaction mechanism

1.2 Boulanger非线性弹簧

Boulanger等建议的宏单元模型可以描述为图2中的三种基本力学现象，见图3。

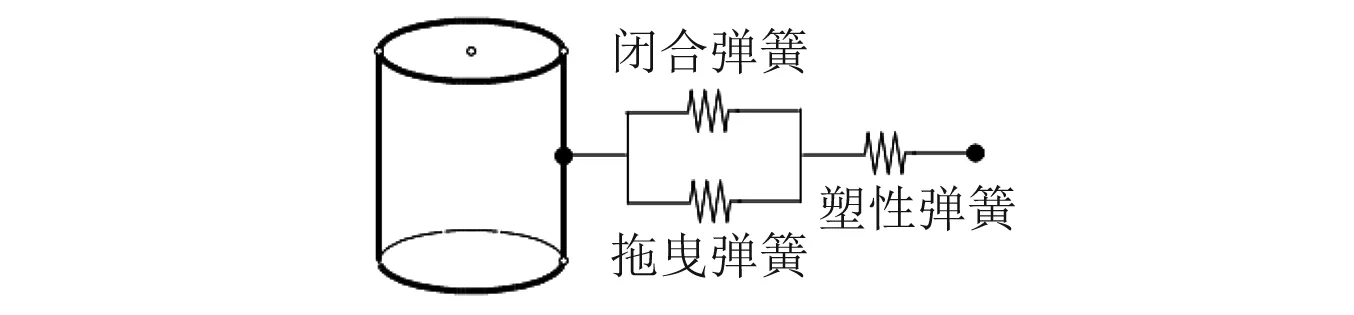
图3 Boulanger宏单元模型 Fig.3 Macroelement proposed by Boulanger

Boulanger等定义的描述桩侧与土之间的横向摩阻力的拖曳元件模型：

(1)

式中，pult为土体极限抗力；y50为桩周土达到极限土抗力一半时桩的挠曲变形；Cd为最大的桩侧横向摩阻力与动力p-y单元中土的极限承载力的比值；pd0为当前荷载方向上拖曳元件的初始摩阻力；yg0为当前荷载方向上拖曳元件的初始位移。

描述桩与土之间的接触与脱离-接触的缝隙元件力学模型为：

(2)

式中：y0+和y0-分别为本阶段荷载作用前桩-土界面的最大正方向间隙和最大负方向间隙，y0+和y0-初始值设为y50/100和-y50/100；系数1.8确保初次加载时pc可以达到pult。

土的材料非线性采用横桩元件p-y模型来描述：

(3)

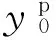
三种力学元件的基本特征，见图4。

图4 塑性弹簧的p-yp曲线Fig.4 p-yp curve of plastic spring

对于Boulanger模型，pult、y50是两个非常重要的参量，各个弹簧的p-y曲线都是通过这两个参量来求得的。不同的研究者给出了pult、y50的不同的确定方法。

在本文的研究中，对于砂土的骨架曲线，采用API规范[8]推荐的方法，Cd=0.2，pult= min[pult1,pult2]，而：

(4a)

(4b)

y50的计算公式为：

(5)

式中：α=φ/2，β=45°+φ/2，K0=0.4，Ka=tan2(45°+φ/2)，γ为土的容重；z为土的深度；D为桩径；φ为土的内摩擦角；k为初始地基模量常数(MN/m3)，其值可参照图5进行选取。

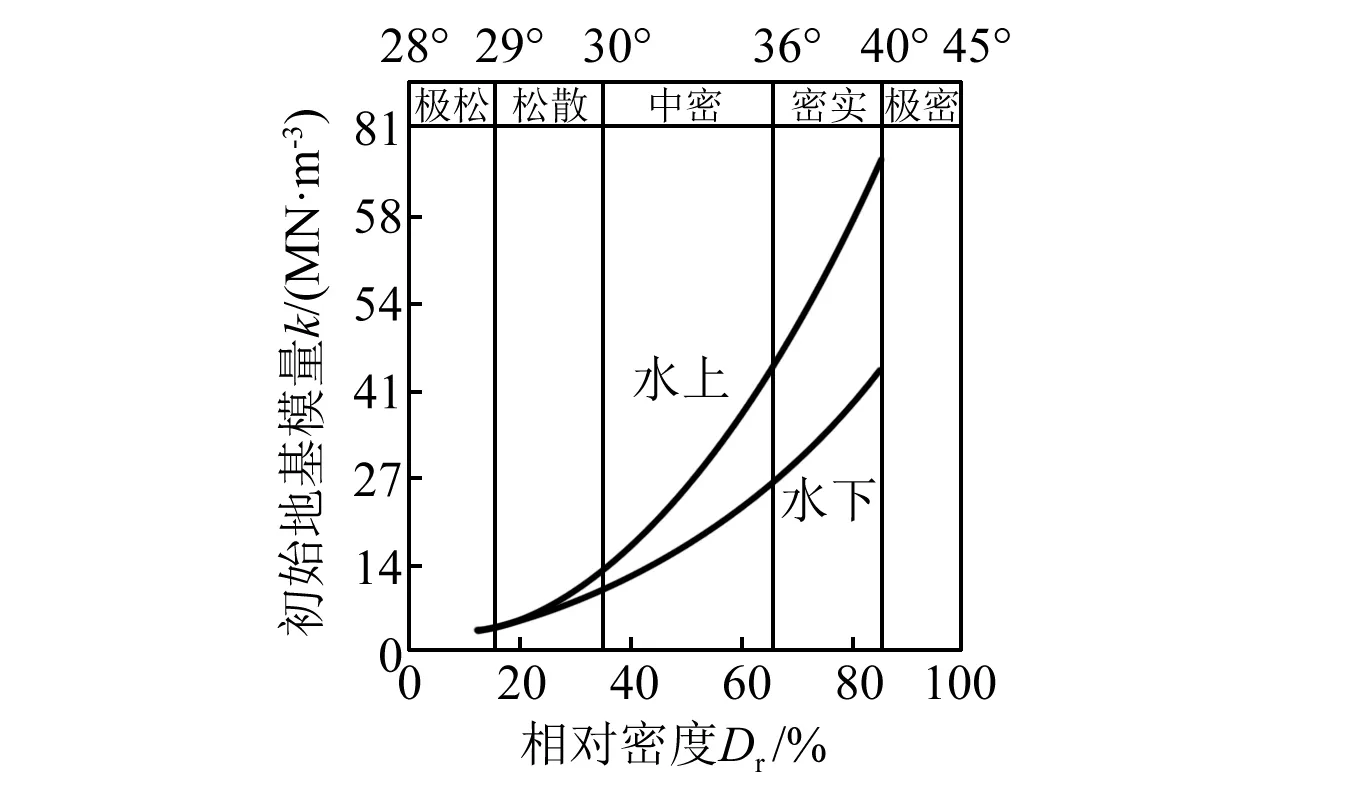
图5 土抗力初始模量Fig.5 The initial modulus of soil resistance

对于黏土， Matlock[9-10]建议

(6)

y50=2.5ε50D

(7)

式中：D为桩的直径；γ′为土的有效容重；z为土的深度；cu为土的不排水抗剪强度；ε50为根据试验得到的应力-应变关系曲线中对应与50%的极限应力时的应变。根据目前现有公布的实验数据，ε50值对于较硬黏土取0.005，中等黏土取为0.01，较软黏土取0.02；J值对于较软黏土取为0.5，对于中硬黏土，Matlock推荐J

取为0.25。

1.3 线性化弹簧

桥梁抗震设计中，常将土的材料非线性性质线性化，且不考虑桩-土之间的脱离-接触，也不考虑拖曳效应。在这样强的假定下，桩-土之间的地震相互作用可以描述为一个线弹性的弹簧，通常配合并联一个黏滞阻尼器，见图6。

图6 线性化宏单元模型Fig.6 Liner macroelement model

确定线性化宏单元模型中弹簧系数的方法有多种，桥梁抗震设计中常用的是基于《公路桥涵地基与基础设计规范》[11]的m系数法。对竖直桩，横桥向弹簧系数按照下式计算：

ki=b1·hi·m·z

(8)

式中：ki为第i层土桩土水平弹簧的刚度系数(kN/m)；b1为桩的计算宽度(m)；hi为桩节点弹簧的所辖桩段长度(m)，可取节点位置上下两个单元长度之和的1/2；m为非岩石地基水平抗力系数的比例系数(kN/m4)；z为节点位置计算深度(m)

m系数法的主要假定[12]包括：① 土为线弹性介质，地基系数在地面(或冲刷线)处为零，并随深度成正比例增加；② 桩基与土之间的黏聚力和摩阻力均不予考虑；③ 在水平力和竖直力作用下，任何深度处土的压缩性均用地基系数表示。

m系数法只适于结构在地面处位移较小的情况，《公路桥涵地基与基础设计规范》建议的m值适用于结构在地面处位移最大值不超过6 mm的情况。但强烈地震使桥梁结构在地面处的位移可能远超过此限值，m系数法的适用性仍有待深入讨论。

另一种较常用的线性化宏单元模型是基于明德林(Mindlin)解采用等效线性化方法考虑土的非线性压缩，也可以满足工程计算的精度要求[13]。土对桩的约束作用及反作用通过等效线性压缩土弹簧KHi表达，彭津建议根据弹性半空间的Mindlin基本解来确定

(9a)

式中：

(9b)

式(9a)和式(9b)中：hi为第i层土的土层厚度；zi为第i层土层中心至地面的距离；B为桩径；Ei为第i层土的等效弹性模量。

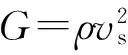
等效弹性模量Ei也可以采用室内试验或工程经验进行估算[14]。因在土体中包含部分残余应变，土力学中的弹性模量通常是用变形模量来表示的，它们具有相同的物理意义。土体变形模量E0与室内实测的压缩模量Es室之间的关系如下[15]：

E0=ψβ(1+e)Es室

(10)

式中：ψ为土体扰动补偿系数，取为1.49；e为地基土孔隙比；对于一般黏土，β约为0.26～0.43；粉质黏土，β约为0.62；粉质砂土，β约为0.74。

《公路桥梁抗震设计细则》[16]中规定在建立桥梁结构的动力空间模型进行动力分析时，土的抗力取值比静力的大，一般取m动=2m静～3m静。

2 例题桥梁基本参数与计算模型

2.1 桥梁构造与基本数据

本文分析的例题桥梁结构的总体几何构造，见图7[17]。桥墩为单柱式，桥墩高15 m，横断面为圆形；承台为4×16的矩形截面；3×1的混凝土钻孔灌注桩，桩径2 m。墩、桩的材料参数，见表1。桩基础埋置于单一的均匀土层中，土下为基岩。考虑典型的砂性土和黏性土，表中土体指标来源于北京轨道交通房山线长阳镇站～稻田站区间的地质详细勘察报告，具体参数指标，见表2。

图7 桥梁几何Fig.7 Geometric dimension of bridge

上部结构质量/T桥梁墩柱材料密度/(Mg·m-3)弹性模量/kPa承台质量/T桩材料密度/(Mg·m-3)弹性模量/kPa30002.63.45×1074002.63.0×107

2.2 计算模型

墩柱、桩采用梁单元建模；承台采用刚体模型；桩-土地震相互作用采用宏单元建模；桥面质量和主梁用一质量块代替，施加在墩顶。采用OpenSees[18]完成计算，力学模型与OpenSees软件中单元的对应关系，见图8[19]。桥墩和桩基础均按1 m划分单元，桥墩共15个单元，每根桩划分30个单元。

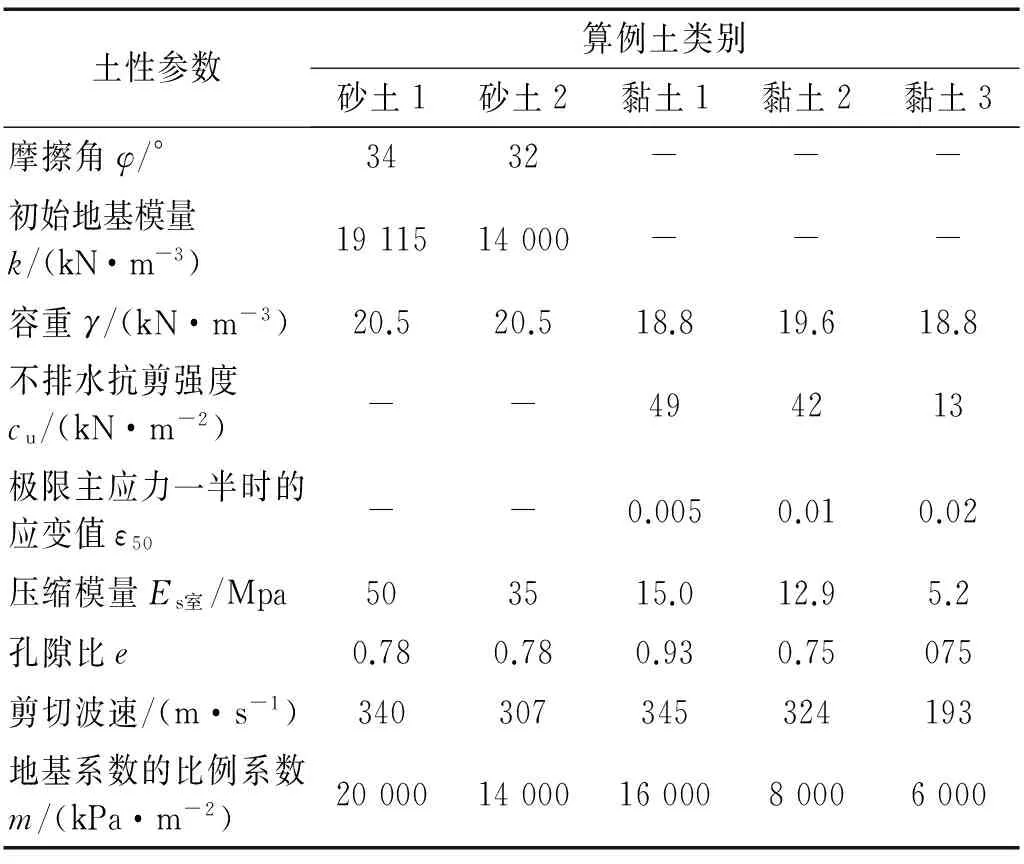
表2 土体基本参数

在水平地震作用下，自由场土体可看作剪切型结构，自由场土体可以简化为一系列剪切弹簧连接的质量块，各质量块之间通过剪切弹簧和阻尼器连接以模拟土层间的相互作用[20]。自由场地模型质点第i层间剪切弹簧刚度Kvi可由式(6)得到：

Kvi=GA/hi

(11)

式中：G为ProShake程序[21-22]计算出的该层收敛剪切模量；A为土柱面积；hi为第i层单元土层厚度。自由场地土柱的面积大小对计算结果的影响较大。A值对于桩周土可以取桩基础承台面积，对于自由场地在不影响结构部分计算精度的前提下，可取得尽量大，一般土体长度取1 000倍[17]的桩径基本能满足要求。

ω是第一振型的自振频率：

(12)

层间阻尼系数Cvi如果采用刚度比例型阻尼，其计算式为：

Cvi=2(βi/ω)Kvi

(13)

式中：β为第i层土的等效线性阻尼；ω为土层的一阶圆频率。

2.3 地震输入

地震动从基岩水平输入，采用EL Centro和Whittier Narrows地震加速度记录，幅值分别为0.097g和0.197g，见图9。

3 计算结果与观察

3.1 地震反应的空间分布规律

计算中采用4种方法确定土弹簧系数。第一种方法采用Boulanger模型，可以考虑土的非线性特征；第二种方法为m法；第三种方法为Mindlin方法，其模量采用等效线性化方法得到；第四种方法也为Mindlin方法，但其模量采用变形模量。考虑图9所示的两种地震波作为输入，EL Centro地震动输入下桥墩与桩的反应见图10，Whittier Narrows地震动输入下的反应见图11。在图10和图11中，B指Boulanger方法，ME1指Mindlin方法，模量采用等效线性化方法确定，

ME2指

Mindlin方法，采用变形模量。

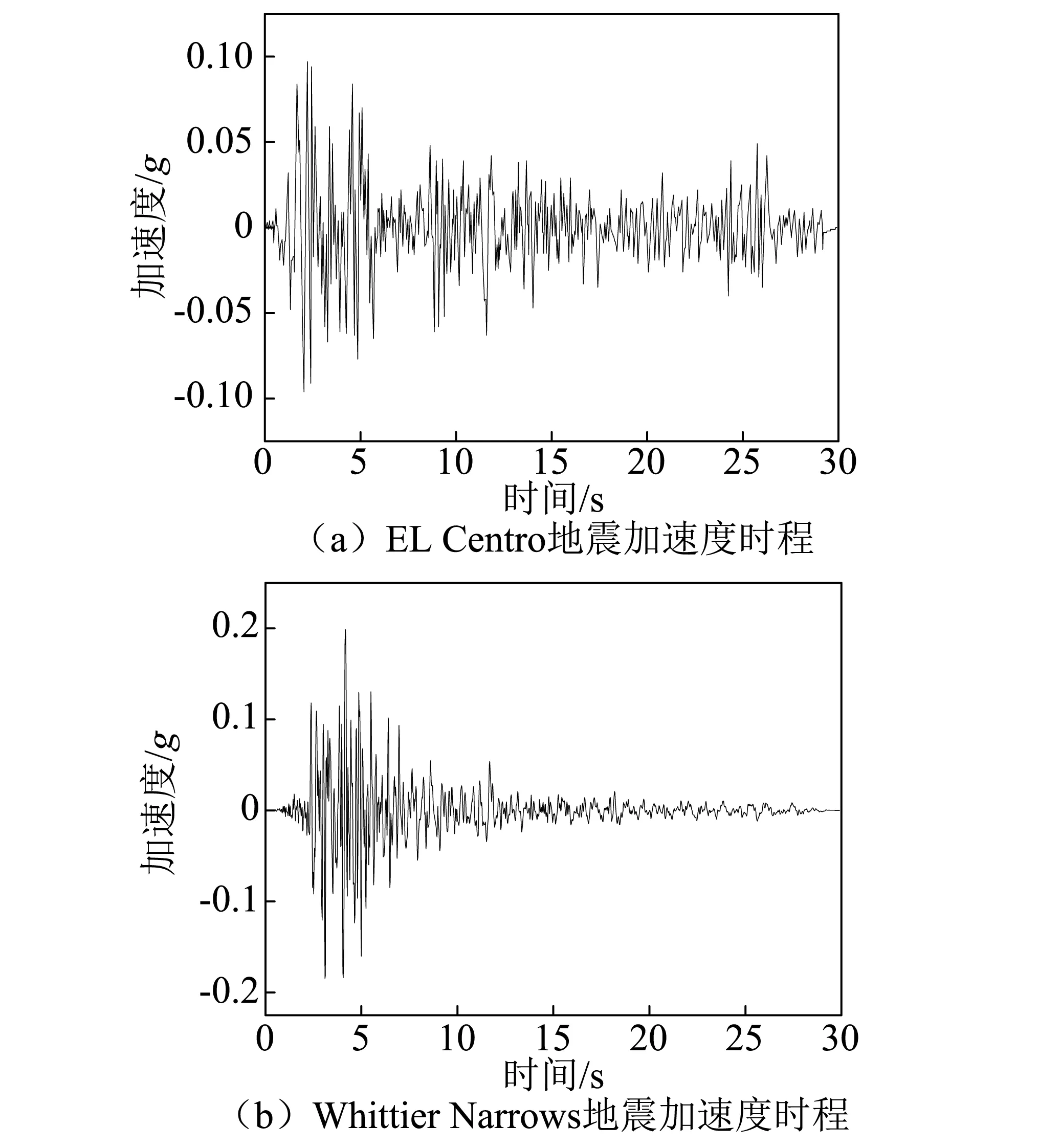
图9 地震动加速度过程Fig.9 Acceleration procedure of earthquake

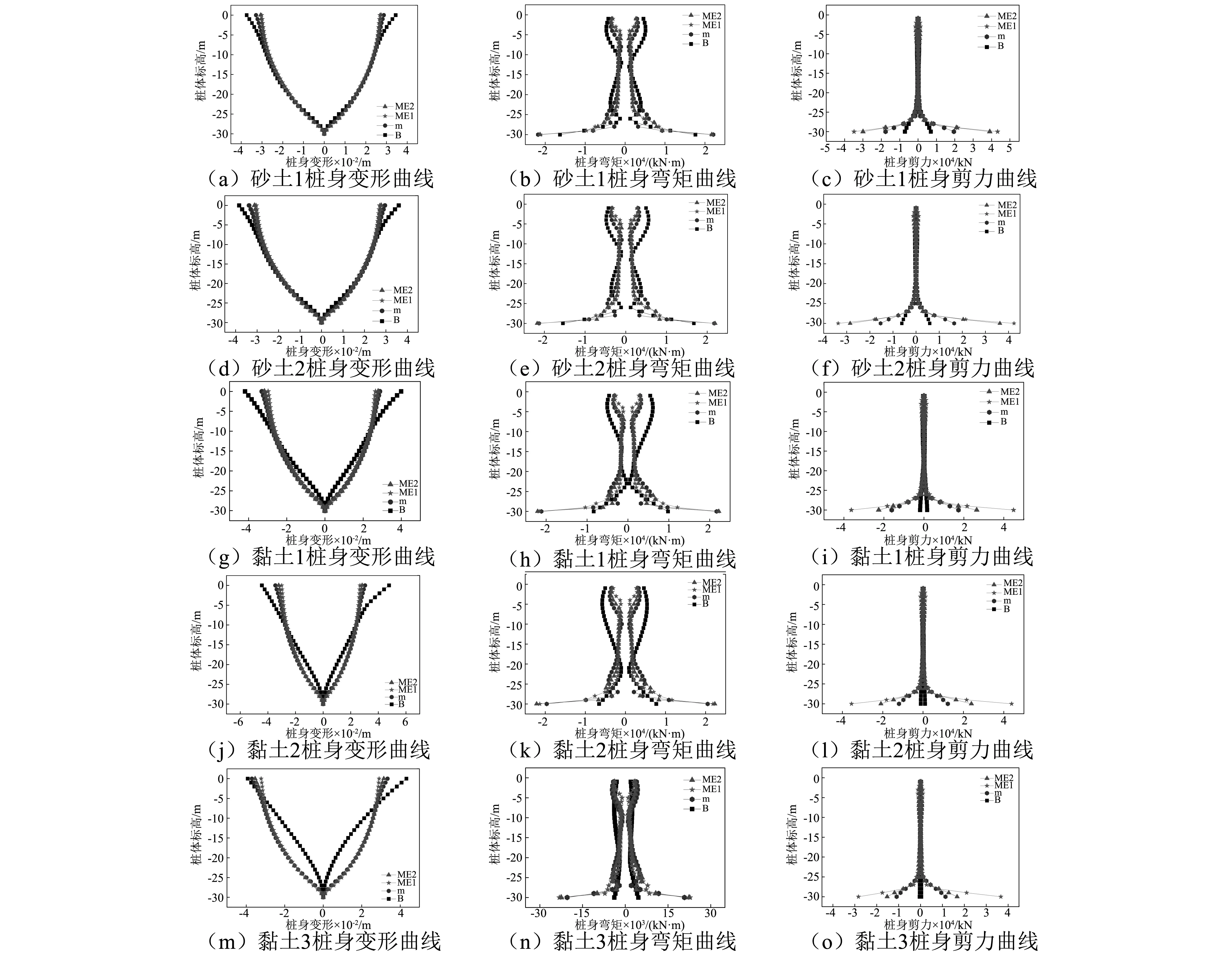
图10 EL Centro 地震波下例题桥梁的反应Fig.10 The response of bridge under EL Centro seismic input

图11 Whittier Narrows 地震波下例题桥梁的反应Fig.11 The response of bridge under Whittier Narrows seismic input

考察的结构反应为特征点的位移、构件的弯矩、剪力。

3.2 地震反应差异的比较

为了描述和比较各种土弹簧方法下得到的算例地震反应之间的差别，定义了如下比值：

(14)

式中：Rm为m法计算得到的地震反应；R为其它方法计算得到的结构反应。

err的计算结果见表3、表4和表5。

表3 柱变形反应err的计算结果

表4 桩身弯矩反应err的计算结果

表5 桩身剪力反应err的计算结果

从桩身变形来看，对于砂土，地表下20～30 m深度范围内，Boulanger方法较m法计算结果偏小，相对偏差可达到26%；ME1和ME2模型计算结果偏大，最大值可达到11%；地表下5～20 m深度范围内，err的数值一般在5%以内；而在地表以下5 m(接近地表)，Boulanger模型的计算结果偏大，偏差达到22%，ME1和ME2计算结果偏小，偏差在10%以内。对于黏土，地表下20～30 m深度范围内，Boulanger方法较m法计算结果偏小，相对偏差可达到80%，ME1和ME2的计算结果偏大，偏差可达到22%；地表下5～20 m深度范围内，Boulanger模型的计算结果明显偏小，偏离达到60%，其他各线性模型的计算结果偏差一般在8%以内；而在地表以下5 m，Boulanger模型的计算结果偏大，最大值达到57%，ME1和ME2方法计算结果偏小，最大值达到13%。

从桩身弯矩来看，对于砂土，地表下20～30 m深度范围内，Boulanger方法较m法计算偏差可达到125%；ME1和ME2计算结果偏差在153%以上。地表下10 m～20 m深度范围内，Boulanger方法的计算结果偏差达到83%，ME1和ME2计算结果偏差在一般在30%以内；而在地表下10 m范围内，Boulanger方法的计算结果偏差达到290%，ME1和ME2方法计算结果偏差可达60%～70%。对于黏土，地表下20～30 m深度范围内，Boulanger方法较m法计算偏差可达到113%，ME1和ME2计算结果偏差在194%以上；地表下10～20 m深度范围内，Boulanger方法计算结果偏差可达到336%，ME1和ME2方法计算结果偏差一般在60%以内；在地表以下10 m，Boulanger方法计算结果偏差达到430%，ME1和ME2方法计算结果偏差普遍在75%以内。

对于桩身剪力，无论是沙土还是黏土，其偏差与弯矩相当或更大。

桥墩的地震响应是抗震研究的重点，针对本例题桥梁，桥墩的弯矩最值出现在墩底，因此对墩底的弯矩进行考察，计算得到的err计算结果见表6。

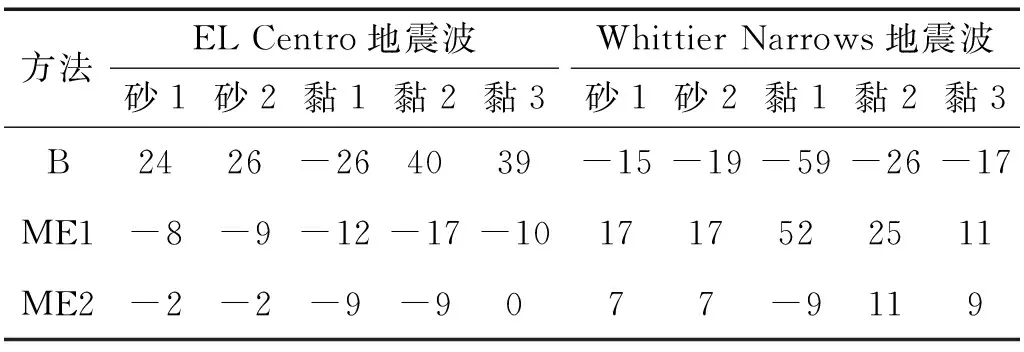
表6 墩底弯矩反应err的计算结果

从墩底弯矩来看，无论是砂土还是黏土，Boulanger方法较m法的计算结果偏差都很大，一般都在20%以上。相比之下，ME1和ME2两种线性方法计算结果偏差要小的多，尤其是ME2方法，偏差一般都在10%以内。

从以上地震反应的差异比较中可以看出，Boulanger模型的计算结果偏差一般都很大。这是因为Boulanger模型考虑的因素相对全面且复杂。Boulanger模型中弹性弹簧表示远场土体的弹性变形，塑性弹簧表示靠近桩基的土体的屈服。模型中的空隙弹簧包括拉伸和闭合弹簧两部分(即前文提到的拖曳元件和缝隙元件)。闭合弹簧用来模拟桩和土之间空隙的打开和闭合，而拉伸弹簧用来模拟桩和土之间的力的传递。当桩在空隙中移动时，土体的残余抗力模拟为拉伸弹簧单元的拉伸力。因此Boulanger模型较好地模拟土体的弹性和塑性变形、桩和土之间空隙的打开和闭合。“m”模型和“Mindlin”模型认为土体是弹性体，即土体只产生弹性变形。相对Boulanger模型而言，考虑的因素单一有限，因此计算结果出现较大差异。

4 对算例计算结果的分析与讨论

4.1 弹簧系数间的差别

第三节中，计算结果的差异来自弹簧系数的差异。表7给出了各种方法刚度的比较，其中Boulanger方法采用的是初始刚度，Mindlin法和m法的土弹簧刚度出于动力分析的目的在静力法得到的刚度基础上已经扩大2.5倍。

表7 各种弹簧模型初始刚度系数的比较

从表7可知，Boulanger方法中的初始刚度相对较小，对于砂土，m法刚度值一般是其7倍～8倍；对于黏土，m法刚度值一般是其几十倍，本例中达到75倍；ME2方法得到的砂土土弹簧刚度一般为m法刚度值的7倍左右，而黏土弹簧刚度一般在m法刚度值附近波动。ME1方法的土弹簧刚度是m法刚度值的十几倍甚至是几十倍，本例中最大者达到70倍。

4.2 桩底弯矩和剪力反应的讨论

观察图10和图11例题桥梁在地震下的反应，桩身弯矩和剪力都在底部出现了最大值。为了解释这种现象，采取两种处理方法：其一是去掉桩身底部8 m范围内的土弹簧，即认为地表下22～30 m范围内的土弹簧刚度系数值为零；二是改变边界条件，将桩与基岩固接改为铰接。以ME1方法为例进行说明，计算得到的桩身弯矩和桩身剪力见图12。

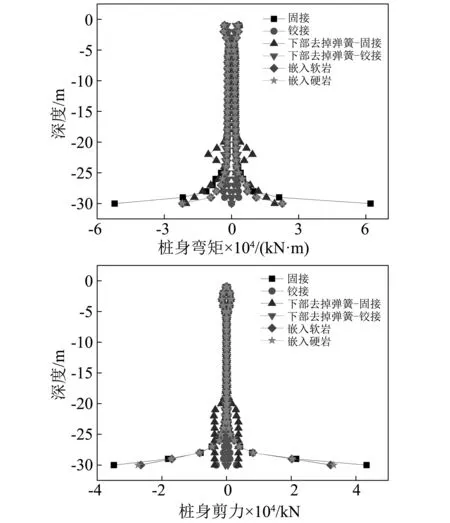
图12 关于弹簧刚度和边界条件对桩底受力反应影响程度的探讨Fig.12 Discussion on the influence of spring stiffness and boundary condition on the seismic response at the bottom of pile

观察图12可知，桩身下部较大的弹簧刚度系数和桩底固接的边界条件对桩底弯矩和剪力影响很大。而本算例采用的是固接边界条件，加之桩身底部土弹簧刚度又很大，使得计算出来的桩底弯矩和剪力非常大。对于工程实际中的嵌岩桩而言，桩底部往往嵌入岩石中一定深度，这里根据岩石的剪切波速换算成Mindlin弹簧施加于桩底，分别计算了软岩和硬岩两种情况，计算结果也见图12。可以看到，考虑岩石的实际力学特征后，计算得到的桩底弯矩和剪力相对桩端嵌固假定显著减小，特别对于软岩石情况。因此在桩基础抗震计算中，无论是摩擦桩还是嵌岩桩，都建议考虑土性和岩性的实际力学参数。

4.3 Boulanger方法对pult和y50两个参数的敏感性

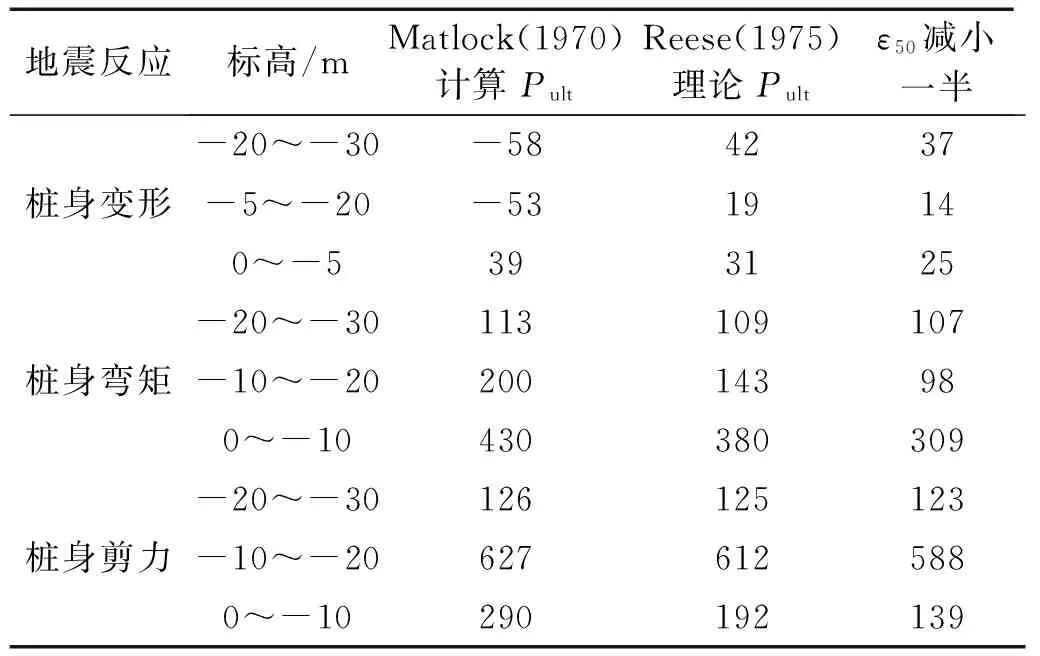
由表7可知，黏土的Boulanger初始刚度较小，这与计算时采用的土体pult和y50两个参数有一定关系。估算土极限抗力pult[23]的经验公式较多，见表8。Matlock(1970)进行比较，探究pult对Boulanger模型初始刚度以及地震反应的影响，具体计算公式见表8。

表8 黏性土条件下表层Np的表达式

对于黏性土，pult=NpcuD，认为随土层深度增加，到达一定深度后，Np保持常数不变，一般在8～12范围内变化。这里取12，以黏土1为例，计算得到的土体抗力见图13。由图13可知，Reese (1975)计算的土体抗力偏大。保持y50不变，采用Reese (1975)计算黏土1的抗力得到Boulanger的初始刚度，与本文中采用Malock(1970)理论计算土体抗力得到的Boulanger的初始刚度二者的比值随深度变化关系见图14。由图14可知，采用不同的土体抗力计算理论对Boulanger初始刚度影响很大。对本文例，如果采用Reese (1975)理论，刚度可提高原来的1～2倍左右，在地表以下20 m范围内刚度提高的更为明显。提高后的初始刚度值与参加比较的m法的刚度值更为接近，且计算得到的地震下的结构反应与m法的偏离程度也减小了很多，具体数值，见表9。

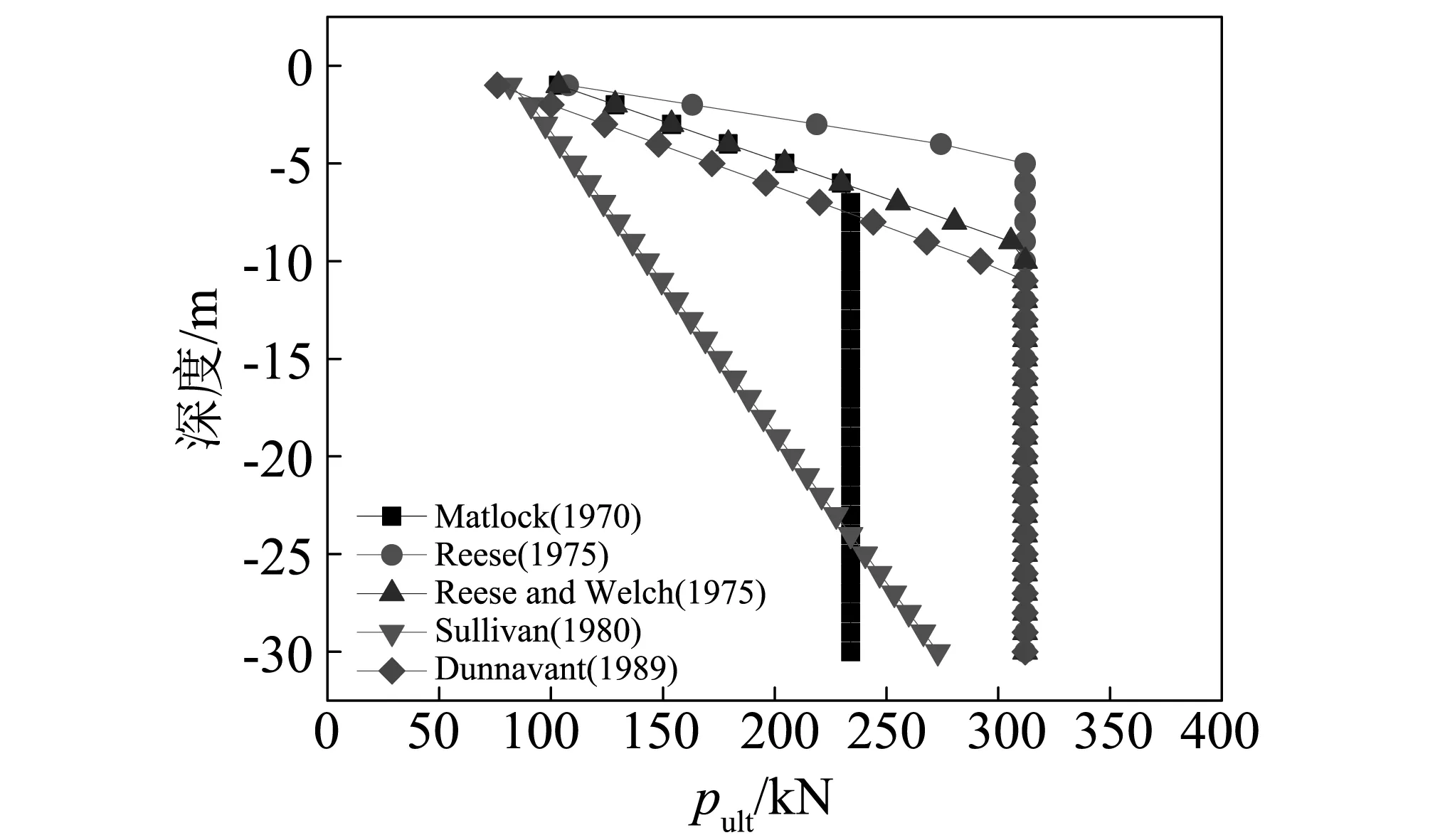
图13 不同理论计算得到的土体PultFig.13 Pult by different theory

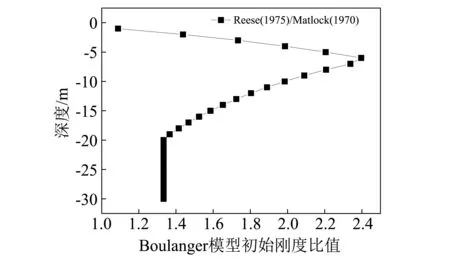
图14 Reese和Matlock初始刚度比Fig.14 Initial stiffness ratio of Reese and Matlock

根据目前现有公布的实验数据，ε50值对于较硬黏土取0.005，中等黏土取为0.01，较软黏土取0.02；同样以黏土1为例，在例题桥梁计算中，ε50值取为0.02，但对以往研究中所提到的较软黏土这种说法很难准确地进行量化，鉴于黏土1的Boulanger初始刚度较小，因此这里将ε50值缩小为原来的一半，重新进行计算，来探究ε50值对模型初始刚度的影响，得到Boulanger的初始刚度与原来的刚度比值随深度变化关系见图15。由图15可知，ε50值缩小一半，Boulanger初始刚度提高一倍左右，计算出来的地震反应相对m法的计算结果偏差程度也比原来小的多，具体数值也见表9。

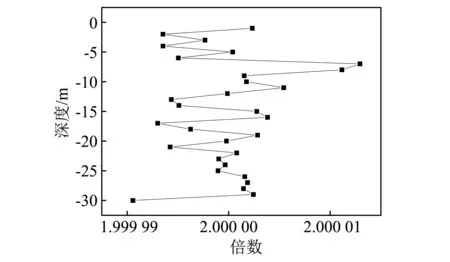
图15 ε50值取为一半时Boulanger模型初始刚度值的比较 Fig.15 Relationship between the initial stiffness ratio of Boulanger model and depth with the half ε50

4.4 土等效模量取值的影响

计算Mindlin土弹簧刚度时，使用的是变形模量，它是根据式(10)换算得到的。由表6可知，黏土的Mindlin土弹簧刚度与m系数法土弹簧刚度比较接近，一般在m系数法刚度值附近波动。而在砂土中，Mindlin土弹簧刚度明显比m系数法土弹簧刚度大一些。这可能与地质勘察资料提供的数据有关。对于砂土，地勘报告鲜有提供压缩模量实测值者，一般给经验值，具有相当大的不确定性。为了更加清晰比较m系数法和Mindlin解两种线性模型，将m法土弹簧刚度根据式(9)将m系数值换算成土体的弹性模量，与计算Mindlin弹簧刚度时采用的两种弹性模量作对比，见图16。

图16 桩土线性模型中弹性模量的对比Fig.16 Comparison of elastic modulus in linear soil-pile model

由图16可知，采用剪切波速在Proshake中进行迭代，最后换算得到的弹性模量比采用土体变形模量，m系数法换算得到的弹性模量大的多，甚至在10倍以上。这是一个需要进一步讨论的问题。

4.5 地震动频谱成分对结构响应的影响

对于本文中的例题桥梁，EL Centro地震波的峰值加速度为0.097g，小于Whittier Narrow地震波的峰值加速度0.197g，但在EL Centro地震波下计算出来的结构响应却比Whittier Narrow地震波下的还要大一些，这与地震动的频谱成分有关。两种地震波的10 Hz以下的傅里叶幅值谱对比，见图17。

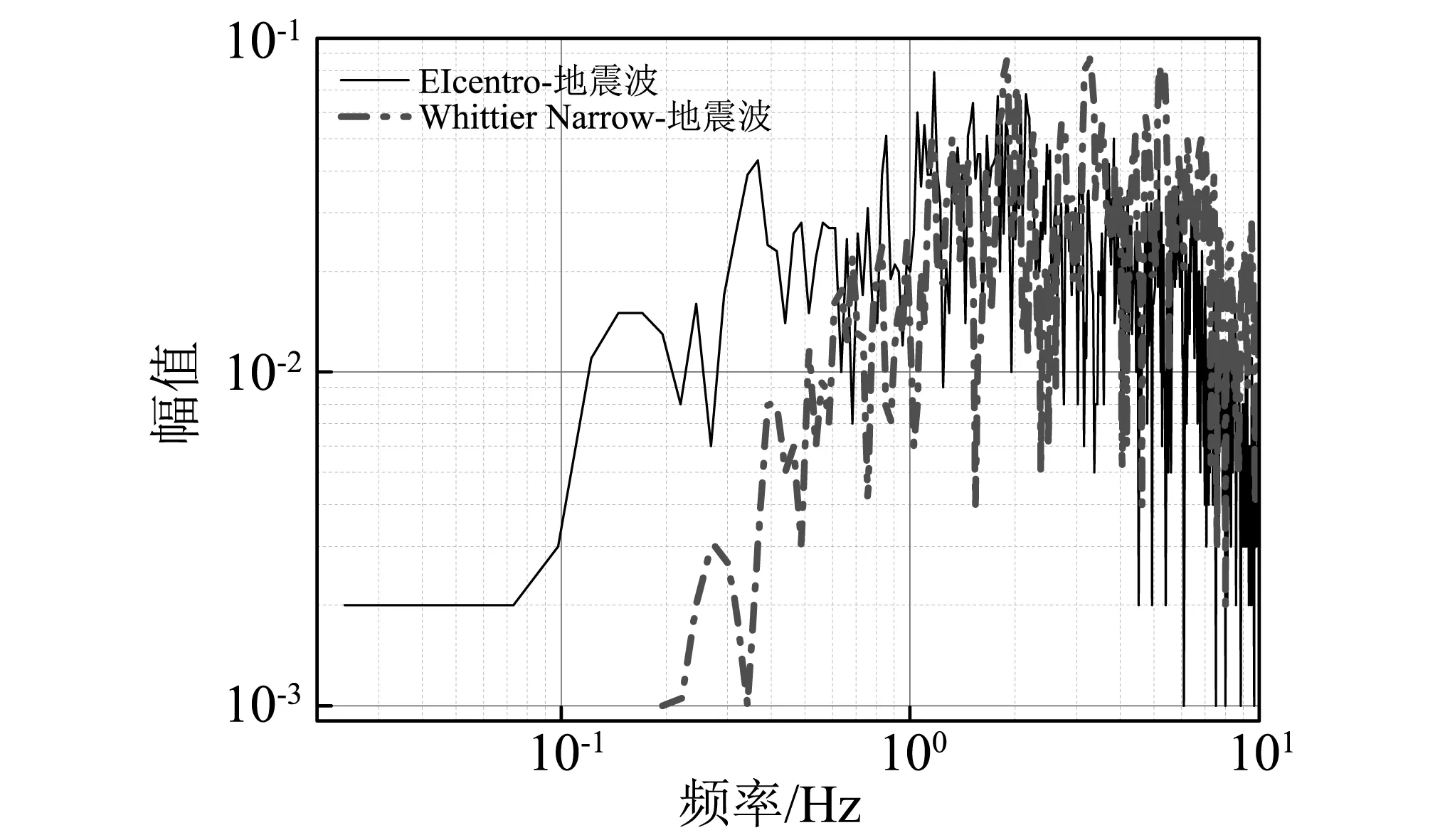
图17 地震波傅里叶幅值谱Fig 17 Fourier amplitude of earthquake wave

由图17可以看到，EL Centro地震波2 Hz以下的成分幅值比Whittier Narrow地震波对应值大得多。本算例结构一阶自振周期，见表10(Boulanger方法取初始刚度)，结构第一阶频率<0.8 Hz，在上述频率范围之内，因此出现EL Centro地震波下计算出来的结构响应却比Whittier Narrow地震波下的还要大的现象。在EL Centro地震波下，地表处的砂土1和黏土1的Boulanger弹簧已经进入了非线性，其力与位移关系见图18。Whittier Narrow地震动下砂土1和黏土1土体基本处于弹性状态，见图19。

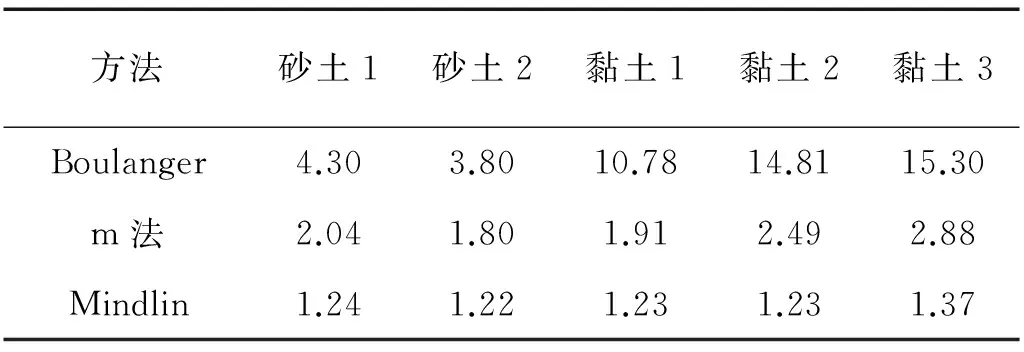
表10 例题桥梁一阶自振周期

图18 E地震波下根据Boulanger模型计算得到的地表处土弹簧力-位移曲线Fig.18 Force-displacement curve of spring on ground calculated from Boulanger model under E wave

图19 WN地震波下根据Boulanger模型计算得到的地表处土弹簧力-位移曲线Fig.19 Force-displacement curve of spring on ground calculated from Boulanger model under WN wave

4.6 Mindlin刚度随土层深度的变化

本节顺便讨论Mindlin刚度随土层深度的变化的规律问题。Mindlin法刚度和m法刚度的比为

(14)

对于例题土层，α/z比值随深度分布关系，见图20，可见该比值随深度呈现曲线变化关系，但土层越深则变化率越小。同时注意到，对于本例，该比值从地表至30桩端，变化范围为0.43～0.49，相对于其它土性参数，该变化范围很小，因此可以取其平均值0.46。这样可以认为Mindlin刚度随深度近似线性变化，与m法接近。如此可以简化Mindlin刚度的计算。

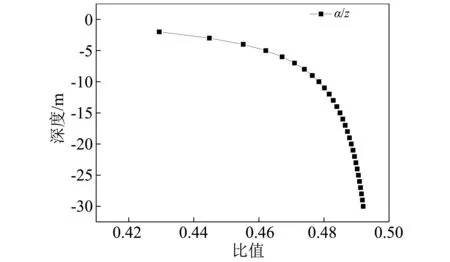
图20 α/z比值随深度变化图Fig.20 Relationship between depth and the ratio of α/z

5 结 论

本文通过一个算例，对常用的集中确定桩土地震相互作用刚度方法造成的桥梁地震反应的离散性进行了讨论，得到了以下初步的结果和结论：

(1) 土性参数对桥梁结构地震反应的影响深大，首先应考虑工程场地的实测值。没有实测值的情况下，设计人员应参考其它资料进行谨慎评估后确定；当采用Boulanger方法时，土体极限抗力pult和y50两个参数重要，需要论述确定的根据。

(2) 采用Mindlin方法时，土模量的取值最为重要，从本文算例结果来看，采用土的变形模量更合理；而使用剪切波速进行等效线性化得到的弹性模量一般要比土体变形模量大的多。

(3) 无论硬岩石、软岩石、还是软土，桩端应根据岩性或土性力学参数确定对应的弹簧，不宜采用嵌固或铰接等假定。

(4) 考虑到土参数的显著不确定性，Mindlin刚度系数表达式中随深度的变化可以近似简化为线性关系，并考虑0.46的乘子。

[1] PENZIEN J, SCNEFFEY C F, PARMELEE R A. Seismic analysis of bridges on long piles[J]. Journal of Engineering Mechanics Division, 1964, 90(3): 223-254.

[2] 张宁勇,王君杰,陆锐. 土-桩-桥相互作用的集中质量模型的比较研究[J].结构工程师,2002(1): 43- 48. ZHANG Ningyong, WANG Junjie, LU Rui. Study on lumped mass models for soil-pile-bridge interaction[J]. Structural Engineers, 2002(1): 43- 48.

[3] 孙利民, 张晨南, 潘龙，等. 桥梁桩土相互作用的集中质量模型及参数确定[J].同济大学学报(自然科学版), 2002, 30(4):409-415. SUN Limin, ZHANG Chennan, PAN Long,et al. Lumped-mass model and its parameters for dynamic analysis of bridge pier-pile-soil system[J]. Journal of Tongji University(Natural Seience), 2002, 30(4):409-415.

[4] 林皋．结构和地基相互作用体系的地震反应分析及抗震设计[M]∥国家地震局工程力学研究所主编中国地震工程研究进展.北京：地震出版杜,1992.

[5] BOULANGER R W, CHRISTINA J C, BRUCE L K, et al. Seismic soil-pile-structure interaction experiments and analyses[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125 (9): 750-759.

[6] 陈国兴．岩土地震工程学[M]．北京：科学出版社，2007.

[7] TACIROGLU E, RHA C S, WALLACE J W. A robust macroelement model for soil-pile interaction under cyclic loads[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(10): 1304-1314.

[8] RP2A-WSD A P I. Recommended practice for planning, designing and constructing fixed offshore platforms-working stress design[C]∥Offshore Technology Conference, 2000.

[9] MATLOCK H. Correlations for design of laterally loaded piles in soft clay[C]∥. Proceeding of the 2nd Annual Offshore Technology Conference. Houston, TX, 1970.

[10] SIMON J. Parameter identification for dynamic analysis of pile foundation using nonlinear p-y method[C]∥ Proceedings of the Second Conference of Junior Researchers in Civil Engineering. Budapest, Hungary:Budapest University of Technology and Economics, 2013.

[11] 中华人民共和国交通部.公路桥涵地基与基础设计规范：JTG D63—2007 [S]. 北京：人民交通出版社， 2007.

[12] 王晓某. 基础工程[M]. 北京：人民交通出版社，2010.

[13] 孙利民,刘东,潘龙,等.桩-土相互作用集中质量模型的土弹簧刚度计算方法[C]∥中国土木工程学会桥梁及结构工程学会年会.南京，2000.

[14] 曾国熙, 叶政青, 冯国栋，等. 桩基工程手册[M]. 北京：中国建筑工业出版社, 1995.

[15] 梁发云.基于多孔介质理论的地基土变形模量估算方法[J].岩土力学，2004，25(7):1147-1150. LIANG Fayun. An approach for estimating deformation modulus of subsoil based on porous medium theory [J].Rock and Soil Mechanics, 2004,25(7):1147-1150.

[16] 中华人民共和国交通运输部. 公路桥梁抗震设计细则：JTG/T B02-01—2008[S]. 北京：人民交通出版社， 2008.

[17] 王青桥, 桥梁桩基础抗震设计方法比较研究[D]. 上海：同济大学桥, 2009.

[18] OpenSees User Manual[S]. Berkeley,CA: University of California.

[19] 燕斌. 桥梁桩基础抗震简化模型比较研究[D]. 上海：同济大学, 2007.

[20] 陆锐. 群桩桥梁结构抗震简化计算方法的比较分析[D]. 上海：同济大学, 2001.

[21] SCHNABEL P B, LYSMER J, SEED H B. SHAKE:a computer program for earthquake response analysis of horizontally layered sites[R]. Berkley:University of California[R]. Berkley:University of California, 1972.

[22] 董正方，轨道交通地下结构横向抗震设计方法与性能指标研究[D]. 上海：同济大学，2012.

[23] DODDS A M, MARTIN G R. Modeling pile behavior In large pile groups under lateral loading[R]. Multidisciplinary Center for Earthquake Engineering Research, 2007.

Parameter analysis on the influence of soil-pile horizontal spring coefficient on the seismic response of bridges

GAO Hao, WANG Junjie, SU Junsheng, SONG Yanchen

(College of Civil Engineering，Tongji University，Shanghai 200092, China)

The concentration parameter method is a major solution in the seismic analysis and design of bridges. From the view angle of finite element, in the concentration parameter method, the stratum semi-infinite space was considered as an abstract mechanical element without geometric dimensions, which is called macro-element. The determination of the model parameters, such as the interaction spring stiffness, the damping and the equivalent mass for the soil around the piles is crucial to the calculation precision. Taking into account common types of soil in engineering and different input of seismic waves, a comparative study was made among the Boulanger model, the ‘m’ method and the Mindlin method (which is equivalent to a linear spring model) based on a large number of parameter analyses, aiming at explaining the key point of the selection of horizontal soil-pile spring coefficient which has a strong influence on the seismic response of bridges.

earthquake； soil-pile interaction； non-linearity； macro-element

国家重点基础研究发展计划(2013CB036305)；国家自然科学基金项目(51278373；51438010)

2016-03-17 修改稿收到日期： 2016-05-27

高昊 男，硕士生，1992年生

王君杰 男，博士，教授，博士生导师，1962年生

TU473

A

10.13465/j.cnki.jvs.2017.14.025