基于功率流的瞬态响应分析及能量波的可视化研究

向 玲， 郑水清， 高雪媛

(华北电力大学(保定) 机械工程系，河北 保定 071003)

基于功率流的瞬态响应分析及能量波的可视化研究

向 玲， 郑水清， 高雪媛

(华北电力大学(保定) 机械工程系，河北 保定 071003)

以钢球和钢块的碰撞作为模型，基于有限元的功率流理论研究了碰撞的瞬态响应。对瞬态响应实现了钢球和钢块碰撞功率流云图及矢量图的可视化，并绘制出了碰撞瞬态响应的时间历程功率流云图及功率流矢量图，从而快速而准确地获得结构体能量在传递过程中任一时刻的大小和方向；提出了弹性体内部能量波的概念，并通过与经典的应力波分析比较说明：基于能量波的功率流云图比应力云图更明显的显示出碰撞过程中的无旋波和等容波，即能量波比应力波更能表现出结构内部的波动性。最后分析了钢球和钢块碰撞时的接触力及碰撞过程中的能量守恒。

有限元；功率流；瞬态响应；能量波；可视化

当结构受到动载荷作用时，其引起的扰动将以波的形式在结构中传播[1]。如果载荷是固定频率的持续载荷，那么波在结构中许多次反射与散射传播后，最终波与波相互叠加形成结构的振动模态，此时关心的是载荷的稳态响应。当载荷是持续时间短的冲击载荷，波在结构中不能形成固定的振动模态，那么此时关心冲击载荷作用的瞬态响应。

结构功率流包含了力与速度的信息，它不仅包含了瞬时能量的大小，还包含了能量流动的方向。在利用功率流研究振动时它还可以反映出力与速度之间的相位信息。因此研究结构功率流对结构内部能量传递过程有重要意义。

研究结构功率流的方法有很多，包括导纳功率流方法 (MPA)[2]、波动方法(Wave Method)[3]、统计能量法 (SEA)[4]、结构声强法(SAI)[5]及功率流有限元法(PFFEM)[6]等。目前为止，众多的研究人员用这些方法对结构功率流进行了大量的研究，Gavric等[7]基于有限元的思想，推导了梁、平板以及壳体结构中的结构声强 (功率流密度) 公式，并给出了简支平板结构的结构声强矢量图。游进等[8]将单频激励的能量流方程推广到随机激励情形。

基于有限元的功率流可视化研究是指在利用数值分析软件、有限元软件等科学计算软件的基础上使功率流以矢量图、云图等图形或动画的形式显示出来。功率流可视化可以更加直观的反应出结构内部能量的传递过程。在功率流可视化方面也有不少学者做出了研究，朱翔等[9]对裂纹损伤结构的功率流进行可视化研究，计算得到了裂纹结构在不同裂纹参数和不同激励频率下的位移响应矢量图、声强矢量图和流线图。张雪冰等[10]对变压器油箱的振动功率流进行了研究，并绘制了振动功率流幅值云图。

关于功率流的研究虽然很多，但大部分是关于振动的稳态响应，而瞬态响应的功率流研究相对较少。Liu等[11]研究了低速碰撞下的钢板功率流瞬态响应，给出了钢板在受到低速钢球碰撞过程中的能量流向矢量图。Zong等[12]利用结构声强理论研究了人体头骨在受到撞击时的瞬态响应。给出了头骨在受到撞击之后的能量大小分布及流向。Halkyard等[13]基于平面波的运动方程提出了一种时域上弯曲波功率流的近似计算方法。

本文利用有限元软件ABAQUS进行建模，以钢球和钢块的碰撞为模型，研究了瞬态响应的功率流可视化方法。提出了能量波的概念，利用ABAQUS二次开发计算并可视化了能量波，并把能量波和应力波做了对比。

1 理论基础

1.1 固体中应力波理论

当静力平衡状态下的弹性体受到载荷作用时，并不是在弹性体的所有各部分都立即引起位移、形变和应力。在作用开始时，距荷载作用处较远的部分仍保持不受干扰。在作用开始后，荷载所引起的位移、形变和应力，就以波动的形式用有限大的速度向别处传播。在以往的论文及书籍中称这些波为应力波，应力波的传播速度与介质密切相关。

当有动力在此弹性体上作用时，则在此弹性体内会产生两种不同的波，分别为无旋波和等容波，其波动方程如下：

无旋波波动方程

(1)

(2)

等容波的波动方程

(3)

(4)

式中：c1、c2分别为无旋波和等容波在弹性体中的传播速度；i=1、2、3代表三个运动方向。

无旋波和等容波是弹性体内弹性波的两种基本形式。波动方程式(1)和式(3)是两个独立的方程，表明在弹性体中存在着两种独立的扰动形式，即两种相互独立的弹性波，并且它们的传播速度不同，由于：

(5)

因此在弹性体内无旋波的波速大于等容波的波速。

1.2 功率流理论

功率流是一个时间相关的矢量，它表示的是结构的瞬时能量，也叫能量流。单位面积上的功率流称为瞬时结构声强。

三维结构声强公式的推导如下：

结构的运动微分方程

(6)

(7)

S为位移矢量

S={u,v,w}

(8)

σ为应力矩阵

(9)

A表示成

(10)

设结构体的单位体积能量为

e=ev+ep

(11)

式中：ev为动能和组成

(12)

ep为势能

(13)

不难证明出

(14)

因此,式(7)可以写成

(15)

式(15)为能量守恒式,令：

(16)

式中：I={Ix,Iy,Iz}称为功率流矢量,表示结构体在振动过程中能量的分布大小及方向。

将式(8)、式(9)代入式(16)得出沿三个坐标方向的分量分别为:

(17)

上式即为弹性体内部瞬时功率流公式。

使用同样的方法可以推出二维瞬时功率流公式为：

(18)

1.3 矢量场可视化

科学计算可视化(Visualization in Scientific Computing)指的是利用计算机图形学和图像处理技术，将工程测量数据、科学计算过程中产生的数据及计算结果转换为图形图像在屏幕上显示出来，并进行交互处理的理论、方法和技术[14],又称为科学可视化,是属于可视化技术中的一门综合学科。

矢量场在科学计算和工程分析中扮演着非常重要的角色,矢量场数据可视化一般都至少要包括三个主要步骤:矢量数据的预处理、矢量数据的映射以及矢量场的绘制和显示[15]。

矢量场的可视化可以绘制静态的矢量图，也可以绘制出由多帧组成的矢量场动画。相比静态的矢量图，矢量场动画更加的直观，而且能够更多的表达出矢量场的信息。

2 结构体内的能量波

而对任一弹性媒质，因为波在弹性媒质中传播时，各质点在其平衡位置附近振动，从而使弹性媒质具有振动动能；又因为振动造成了各质点之间的距离发生改变，媒质发生形变，从而使之具有形变势能。振动动能与形变势能之和称此媒质中弹性波的能量。

根据结构体内功率流的公式推导可以看出，功率流所反映的正是弹性波所携带的能量。当结构体受到载荷激励时，在结构体内部就会产生弹性波。以应力和应变扰动的传播形式反映的弹性波称为应力波，同样以能量扰动的传播形式反映的弹性波称为能量波。应力波表现为结构体内质点应力、应变状态的变化，而能量波表现为质点应力、应变及速度的变化，能量波反映的是质点动能和势能的总和。由于以功率流理论所表达出来的能量波是一种瞬时能量，所以能量波也可称为功率波。

3 钢球撞击钢块的瞬态响应分析

3.1 钢球撞击钢块的模型

取一个钢球和一个钢块相碰作为研究模型，见图1。钢球直径为10 mm，以1 000 m/s的速度撞向一个边长为100 mm的方形钢块。钢块右端固定在墙上，忽略重力的影响。

由于主要观察钢块内部的能量变化，所以假设钢球为刚性球，即在碰撞过程中不发生变形。钢块的密度为7 800 kg/m3,弹性模量2.1×1011Pa，泊松比0.3。

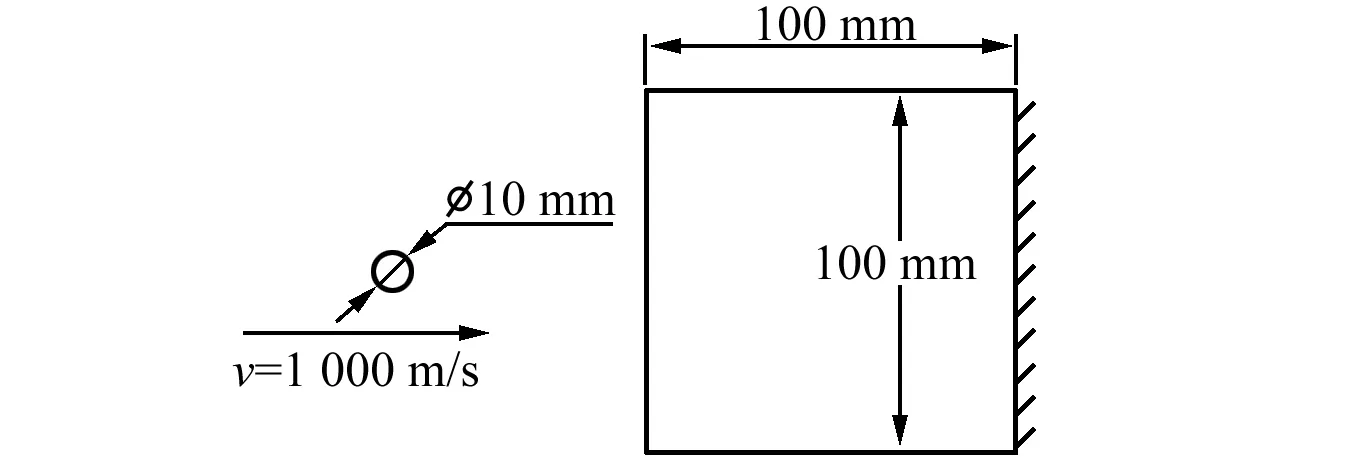
图1 钢球和钢块碰撞模型Fig.1 The collision model of steel ball and steel block

使用有限元软件建立钢球和钢块碰撞模型，对碰撞过程进行瞬态动力学分析。由于能量在结构内部传递过程中会受到黏性阻尼的影响，黏性阻尼越大，总的动能和内能衰减的越快。在建模过程中设置线性粘性阻尼系数为0.06。由于风阻尼、干阻尼等其它阻尼对钢块结构体内能量的传递过程的影响不大，因此论文中没有考虑。

3.2 碰撞的瞬态响应分析

3.2.1 碰撞过程中的应力波及功率流

取模型中和钢球速度方向平行的过钢球圆心的竖直剖面来进行碰撞过程分析。图2～图5为钢球和钢块碰撞2 μs、10 μs、17 μs、21 μs时刻响应特征图。

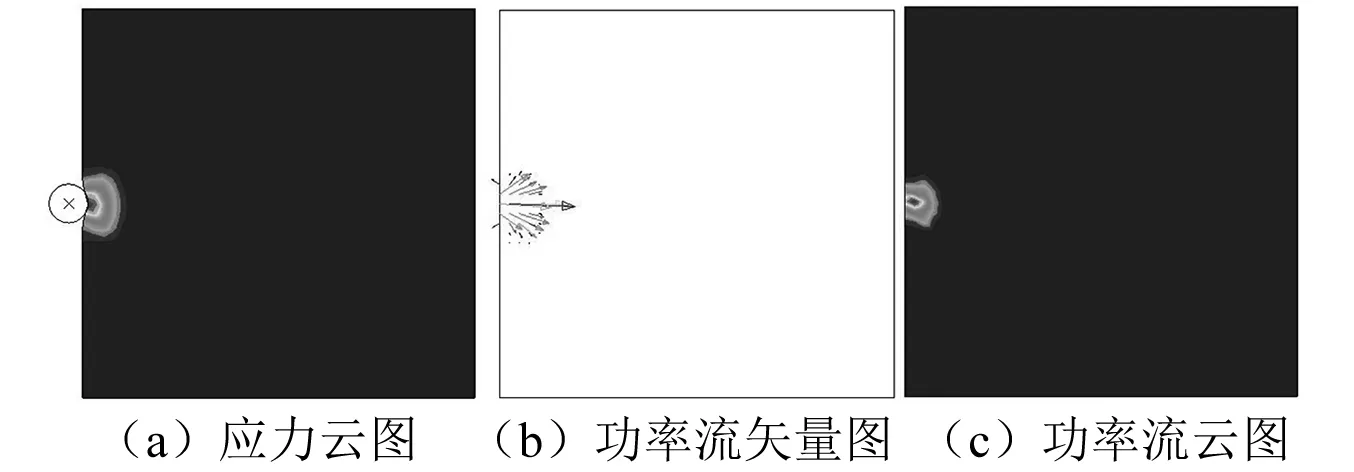
图2 2 μs时刻响应特征图Fig.2 Response characteristics of 2 μs moment

图3 10 μs时刻响应特征图Fig.3 Response characteristics of 10 μs moment

图4 17 μs时刻响应特征图Fig.4 Response characteristics of 17 μs moment

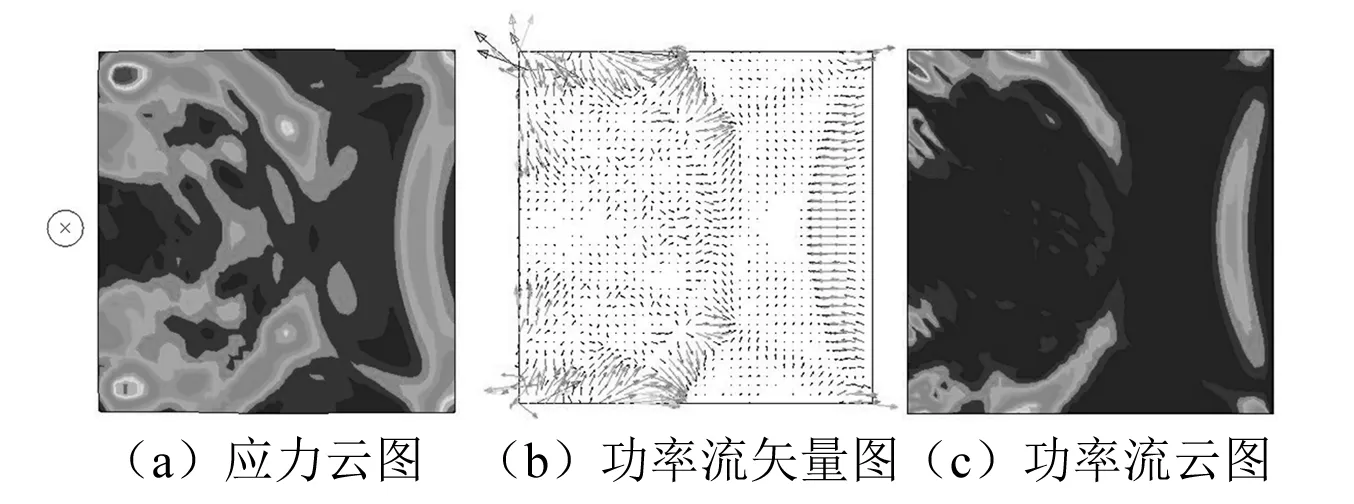
图5 21 μs时刻响应特征图Fig.5 Response characteristics of 21 μs moment

从图3可知，在10 μs时刻同时产生了一前一后的两个波。将图3和图4相对比可知，这两个波的波速不一样。前一个波的速度大于后一个波的波速，根据对比前面理论分析可知，前一个波为无旋波，后一个波为等容波。由式(5)计算得

(19)

由此可知，无旋波的波速是等容波的1.871倍，这和图中所显示的差异基本相同。

从功率流矢量图可以清楚的表示出下一刻能量的传递方向，当能量发生反射时，功率流矢量的方向会随之发生改变(如图5)，结合功率流矢量图和功率流云图可以快速而准确的得出结构体中的能量在传递过程中任一时刻的大小和方向。

从应力云图和功率流云图相比较可知，虽然是在同一时刻，但是两个云图显示应力波和能量波有所不同。因为应力云图显示的只是在钢块内部应力的大小，由式(13)可知，应力的大小只能反映质点势能的大小，而功率流云图显示的是应变能和动能大小的总和。说明在功率流云图上显示的波是一种能量波。因此得出：应力波代表着弹性波所携带应力的大小，而能量波代表着弹性波所携带能量的大小。

通过对比应力云图、功率流矢量图和功率流云图可知，功率流云图可以比应力云图更加清楚的显示出无旋波和等容波的波峰的位置，并且从功率流矢量图可以清楚的表现出无旋波和等容波下一时刻的传递方向。把功率流云图和功率流矢量图统称为功率流图，在功率流图上所表现的弹性波为能量波。则由以上分析可得，在有限元分析过程中能量波的传播形式比应力波的传播形式更能反映的弹性波的波动性质。

3.2.2 能量守恒

在ABAQUS的动力学分析过程中，能量守恒是评价分析结果的一个重要指标[16]。在本次动力学仿真过程中，存在变化的能量有动能(ALLKE)、应变能(ALLSE)及由黏性阻尼产生的黏性耗散能(ALLVD)。其各自的能量变化，如图4～图6所示。

图6所示的是钢球和钢块作为整体能量变化的总和，而图7和图8中分别是钢块和钢球能量的变化。从图6可知，在碰撞过程中的总能量(ETOTAL)和基本保持没有发生变动，说明满足能量守恒条件。由于钢球是刚性体所以在钢球内部不存在应变能。在整个过程中能量的变化满足以下能量守恒关系：

ETOTAL=ALLKE+ALLSE+ALLVD

(20)

图6 在碰撞过程中整体能量的变化Fig.6 The total energy change in the process of collision

从图6和图7可知，在碰撞过程中，钢块内部的动能和应变能是由钢球的动能传递的。所以钢球在碰撞初始和碰撞结束时的动能是不同的。速度也是不同的。结合“3.2.1”分析可知，钢球传递给钢块的能量在钢块内部是以能量波的形式在钢块内部传递并耗散。

从图6中还可知，能量在钢块内部传递过程中，钢块内部的应变能和动能在不发生反射的情况下基本上是保持平稳下降的，但是当存在能量波的反射时(图6中17μs时刻)，应变能就会和动能相互的转换，在固定端反射时应变能变大，动能变小。相应的在自由端反射时动能变大而应变能变小。

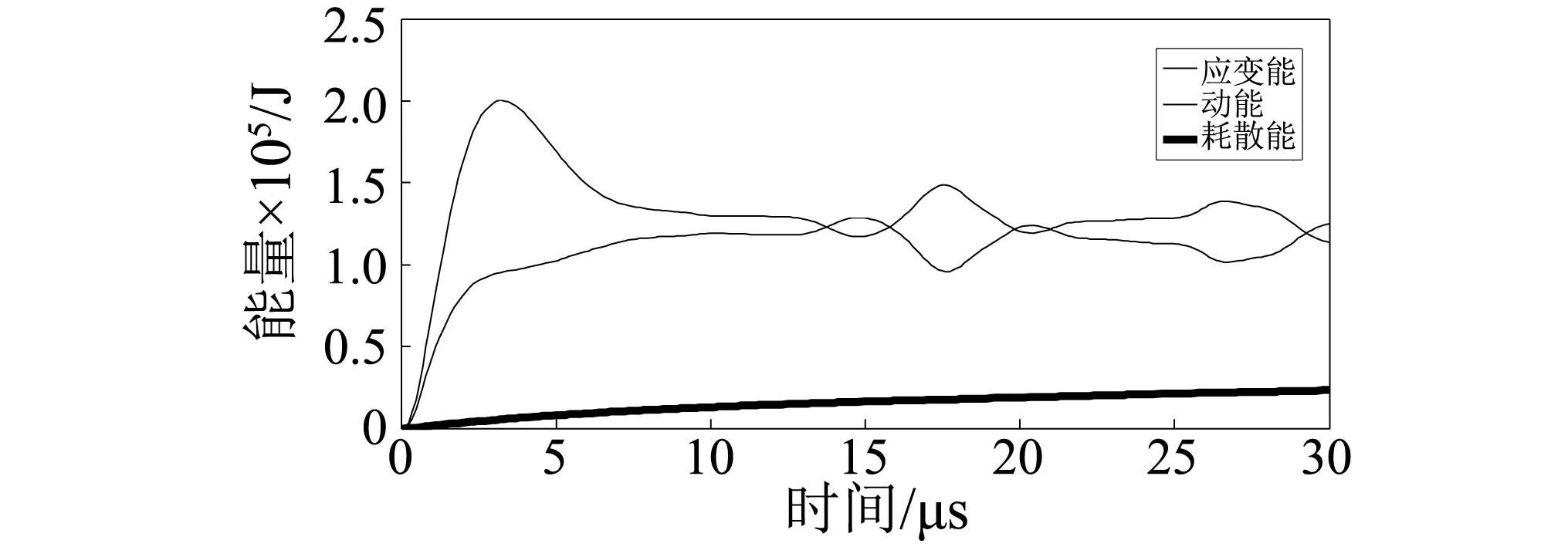
图7 在碰撞过程中钢块能量的变化Fig.7 The energy change of the steel block in the process of collision

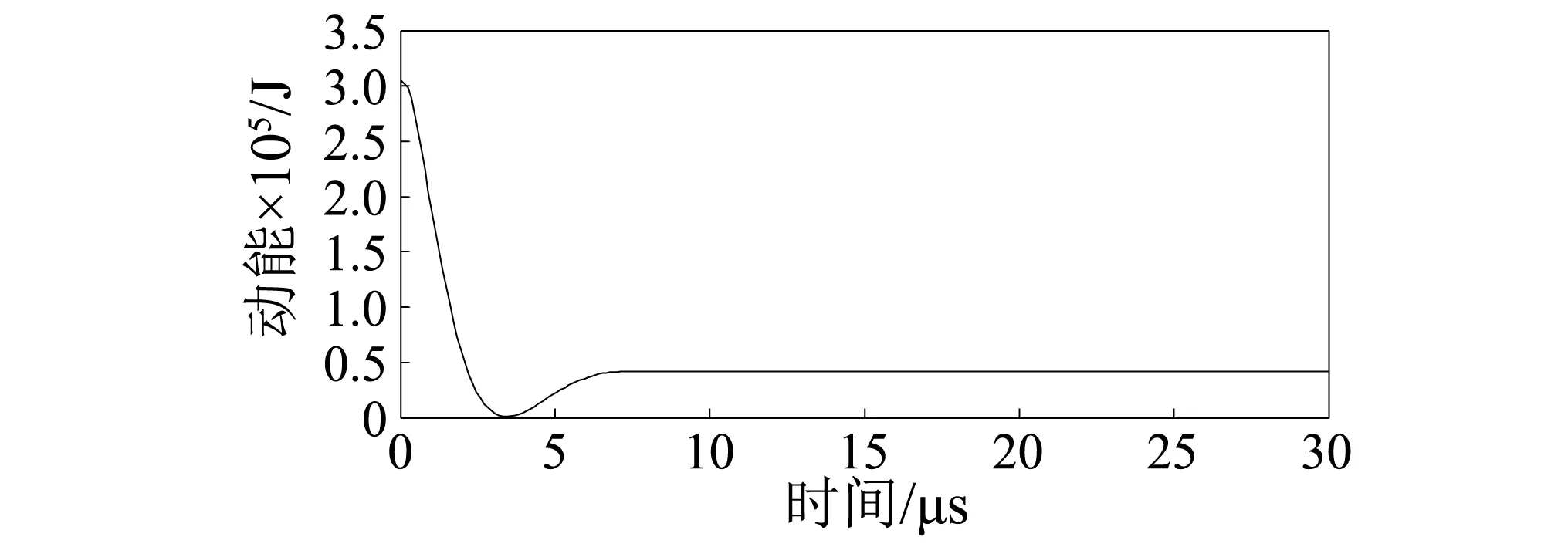
图8 在碰撞过程中钢球能量的变化Fig.8 The energy change of the steel ball in the process of collision

3.2.3 碰撞力分析

在钢球和钢块碰撞过程中，碰撞的接触力大小如图9所示。

图9 碰撞过程中的接触力Fig.9 The contact force in the process of collision

从图9可知，碰撞是在7μs时钢球和钢块开始分离。从接触力曲线的形状可以看出，在碰撞过程中的接触力并非是理想的半个正弦。结合能量守恒及碰撞过程分析可总结出以下两个原因：①由于在碰撞过程中，钢球和钢块的接触面积存在变化。钢球的压进阶段接触面积是越来越大，而钢球的反弹阶段接触面积越来越小。②由于在碰撞过程中存在能量的传递(见图6)。钢球在碰撞初始和碰撞结束的速度不同(见图8)，这导致了钢球的压进阶段和反弹阶段的加速度的不同，从而导致了接触力的不同。

4 结 论

(1)验证了实体内部的同时存在无旋波和等容波，并且说明了两个波的波速不相同。无旋波的波速大于等容波的速度。

(2)利用有限元软件开发并可视化了功率流的矢量图及云图，并生成碰撞的瞬态响应的功率流矢量图动画及功率流云图动画。这些动画可以直观的反映出结构内部能量波的传递及反射过程。

(3)给出了能量波的概念，对比了能量波和应力波。能量波不仅包含有动能，还包含有应变能。并且在有限元分析过程中能量波的传播形式比应力波的传播形式更能反映的弹性波的波动性质。

(4)分析了钢球和钢块碰撞时的接触力及碰撞过程中的能量守恒。在碰撞过程中接触力并不是半个正弦曲线，而且在碰撞过程中钢球的一部分动能会传递给钢块，转化成钢块内部质点的动能及应变能，并且这些能量在钢块内部以能量波的形式传播。

(5)能量波和应力波一样在传递过程中也会发生反射，散射及波与波叠加等特征现象。这些需要后期的继续研究。

[1] GRAFF K F. Wave motion in elastic solids[M]. Oxford: Claremdon Press, 1975.

[2] CUSCHIERI J M. Structural power-flow analysis using a mobility approach of an L-shaped plate [J]. Journal of the Acoustical Society of America, 1990,87(3):1159-1165.

[3] KESSISSOGLOU N J. Power transmission in L-shaped plates including flexural and in-plane vibration [J]. Joumal of the Acoustical Society of America, 2004, 115(3): 1157-1169.

[4] LYON R H. Statistical energy analysis of dynamical systems：theory and application[J] . Annals of Probability an Official Journal of the Institute of Mathematical Statistics,1975,28(9):430.

[5] WILLIAMS E G. A technique for measurement of structure-bome intensity in plates[J]. Joumal of the Acoustical Society of America，1985，78(6):2061-2068.

[6] NEFSKE D J, SUNG S H. Power flow finite element analysis of dynamic system: Basic theory and application to beams [J] .Transactions of the ASME， 1989, 111:94-100.

[7] GAVRIC L, PAVIC G. Finite element method forcomputation of structural intensity by the normal mode approach[J]. Journal of Sound and Vibration, 1993, 164(1)：29-43.

[8] 游进，李鸿光，孟光. 耦合板结构随机能量有限元分析[J]. 振动与冲击, 2009, 28(11): 43-46. YOU Jin, LI Hongguang, MENG Guang. Random energy finite element analysis of coupled plate structures[J]. Journal of Vibration and Shock, 2009, 28(11): 43-46.

[9] 朱翔，李天匀. 基于有限元的损伤结构功率流可视化研究[J]. 机械工程学报, 2009, 45(2): 132-137. ZHU Xiang, LI Tianyun. Visualization research on the power flow characteristics of damaged structures based on the finite element method[J]. Journal of Mechanical Engineering, 2009, 45(2): 132-137.

[10] 张雪冰，饶柱石，塔娜，等. 变压器油箱振动功率流研究[J]. 振动与冲击, 2009, 28(5): 188-191. ZHANG Xuebing, RAO Zhushi, TA Na, et al. Power flow of transformer tank[J]. Journal of Vibration and Shock, 2009, 28(5): 188-191.

[11] LIU Z S, LEE H P, LU C. Structural intensity study of plates under low-velocity impact[J]. International Journal of Impact Engineering , 2005, 31(8): 957-975.

[12] ZONG Z, LEE H P, LU C. A three-dimensional human head finite element model and power flow in a human head subject to impact loading[J]. Journal of Biomechanics , 2006, 39(2): 284-292.

[13] HALKYARD C R, MASSON P. Time-domain flexural wave intensity estimation in orthotropic Kirchhoff plates[J]. Journal of Sound and Vibration, 2016, 368(28): 55-70.

[15] POST F, VON WALSUM T. Fluid flow Visualization[C]∥ Hager H, Muller H, Nielson G M.(Eds)Focus on Scientific Visualization.Spring-Verlag, 1993.

[16] 朱跃峰. 基于ABAQUS的显式动力学分析方法研究[J]. 机械设计与制造, 2015(3):107-109. ZHU Yuefeng. Research on analysis methods of explicit dynamics based on ABAQUS[J]. Machinery Design & Manufacture, 2015(3):107-109.

Transient response analysis based on the power flow and the visualization of energy wave

XIANG Ling, ZHENG Shuiqing, GAO Xueyuan

(Mechanical Engineering Department, North China Electric Power University, Baoding 071003, China)

Study the transient response due to a collision based on the theory of power flow finite element method with the collision model consisting of a steel ball and a steel block. Realize the visualization of power nephogram and power vectorgraph for the transient response . And draw out the power nephogram animation and vectorgraph animation for the transient response in the process of collision to obtain the magnitude and direction of energy transmission quickly and accurately at any moment in the structure body. Put forward a concept of energy wave in the elastomer. Through comparing with the stress wave, it is verified that the power nephogram is more obvious than the stress nephogram in showing the irrotational wave and shear wave in the process of collision. That is to say, the energy wave is better than the stress wave in showing the volatility in the elastomer. Analyse the contact force and energy conservation in the process of collision in the end.

finite element;power flow;transient response;energy wave;visualization

国家自然科学基金(51475164；51675178)

2016-03-29 修改稿收到日期： 2016-05-19

向玲 女，博士，教授，1971年生

TH113

A

10.13465/j.cnki.jvs.2017.14.023