考虑温度和湿度的风机最大功率跟踪控制

苏勋文 徐殿国 杨荣峰 岳红轩

（1. 黑龙江科技大学电气与控制工程学院 哈尔滨 150027 2. 哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001 3. 许继集团有限公司 许昌 461000）

考虑温度和湿度的风机最大功率跟踪控制

苏勋文1,2徐殿国2杨荣峰2岳红轩3

（1. 黑龙江科技大学电气与控制工程学院 哈尔滨 150027 2. 哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001 3. 许继集团有限公司 许昌 461000）

为研究环境因素对风机最大功率点跟踪（MPPT）的功率信号反馈算法（PSF）的影响，首先根据温度和湿度与空气密度的数学关系，分析温度和湿度影响PSF算法的机理。然后提出考虑温度和湿度的最优功率曲线获取方法，给出计及温度和湿度的PSF算法实施过程和具体流程，该方法考虑了风机损耗对PSF算法的影响。最后在Matlab/Simulink分析平台上，搭建基于功率信号反馈算法的双馈机组模型，仿真分析和风电场现场测试验证了考虑温度和湿度的PSF算法能够获得较高的风能转换效率。

温度 湿度 功率信号反馈算法 风电机组 最优功率曲线

0 引言

近年来风力发电得到了快速发展，如何获得风机最大风能转化效率的算法也越来越受到人们的关注。最大功率点跟踪（Maximum Power Point Tracking, MPPT）算法有尖速比法、最优力矩法、功率信号反馈法、爬山法、模糊算法、神经网络法等[1-14]，对于转动惯量大且叶轮参数已知的大中型机组，通常采用功率信号反馈法[14]。

目前，大多数风电机组制造商在选择风电机组的控制策略时，通常认为空气密度不变或仅根据风电场年平均空气密度来确定机组最优控制策略，很少考虑温度和湿度变化对风电机组输出功率产生的影响，从而导致风电机组输出功率达不到厂家设计的最优输出功率值。

文献[1]综述了风电机组各种MPPT算法，指出间接功率法需要空气密度数值，否则将影响风机效率，而且空气密度变化会影响爬山算法的最优功率曲线。文献[15]分析了风机最大功率点控制的影响因素，指出温度变小，将导致空气密度变大，使得减小转矩增益（De-creased Torque Gain, DTG）跟踪控制的转矩增益系数Kd和基于收缩跟踪区间跟踪控制的补偿系数α 增大，但该文仅给出结果，没有分析其影响机理。文献[16]给出了一种考虑高度和温度的自适应空气密度变化的风电机组最优转矩控制方法。实际上，风机所处的不同温度、海拔高度、气压和湿度会导致空气密度随时间波动。上述方法没有考虑湿度和风机损耗的影响，没有进行深入的机理分析和仿真分析。风机实际控制中是否需对四个环境因素都进行测量需要进一步研究。

为此，本文以MPPT算法中功率信号反馈（Power Signal Feedback, PSF）算法为例，首先分析环境因素影响PSF算法的机理；其次考虑机组损耗，给出一种获得标准空气密度最优功率曲线的方法；然后提出一种计及温度和湿度的风机功率信号反馈新算法，最后仿真和风场测试验证方法的正确性。

1 温度和湿度影响功率信号反馈算法的机理

1.1 功率信号反馈算法

功率信号反馈算法：已知双馈风电机组的最优功率曲线，输入转速，通过最优功率曲线得到对应的最优有功功率，最优有功功率与实际功率进行比较控制。算法如图1所示。图2为ω -P最优功率曲线。

图1 双馈机组PSF算法Fig.1 PSF algorithm with DFIG

图2 最优功率曲线Fig.2 Maximum power curves

图2中最优功率曲线ω -P的表达式为

1.2 空气密度对PSF算法的影响分析

从式（1）可以看出，空气密度会影响最优输出功率。取风速分别为7m/s、8m/s、9m/s，图3中实线和虚线分别为空气密度是1.1kg/m3、1.3kg/m3的风机最优功率曲线。

图3 空气密度不同的最优功率曲线Fig.3 Maximum power curves for different air densities

从图3可以看出，空气密度变化时，风机的最优功率曲线会变化，分别把两个空气密度代入式（1），得到相同转速对应的最优有功功率比值为

由式（2）可见，空气密度变化会改变最优功率曲线的最优功率参数值，因此为保证风电机组最优运行，需要监测空气密度的变化。

为了进一步分析空气密度对最优控制算法的影响，以风速为8m/s为例，分别给出标准空气密度（ρ =1.225kg/m3）最优功率曲线和空气密度为1.6kg/m3的最优功率曲线，如图4所示。

图4 两种功率曲线下风机输出功率差Fig.4 Output power difference of wind turbines under two power curves

图4中，假定开始时风机运行在标准空气密度条件下，稳态运行点为A，当空气密度突变为1.6kg/m3后，空气密度变大导致风机输入机械功率变大，风机加速，按照空气密度为1.225kg/m3的最优功率曲线，风机则稳定运行在B点。如果采用考虑空气密度的MPPT控制，根据空气密度为1.6kg/m3的最优功率曲线，风机则稳定运行在C点，B点和C点作图可知，相比不考虑空气密度的MPPT控制，考虑空气密度的MPPT控制将获得更大的风机输出功率，增加的功率差如图中OB段所示。

1.3 温度和湿度与空气密度关系

影响空气密度的环境因素有气压、温度、高度和湿度。气压为干燥空气气压和水蒸气气压之和。

干燥空气气压和高度有关，关系式为

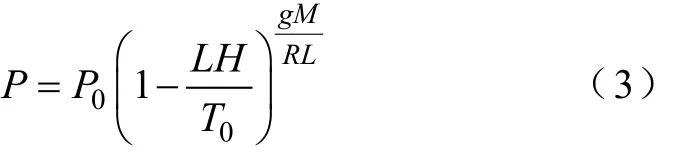
式中，标准大气压P0=101 325Pa；常温为15℃，标准温度T0= 15 + 273.15 = 288.15℃；温度递减率L= 0.006 5K/m；H为高度（m）；理想气体系数R= 8.314 47J/(mol·K)；重力加速度g = 9.806 65m/s2；摩尔质量M

=0.028 964 4kg/mol。由式（3）可以看出，干燥空气气压仅与高度有关，高度越高，气压越低。由于风机高度固定，干燥空气时，空气密度仅与温度有关；非干燥空气时，空气密度与温度和湿度有关。

1）温度与空气密度的数学模型

当不考虑湿度时（即相对湿度取0%，为干燥空气），空气密度仅与气压（气压与风机高度有关）和温度有关，其数学关系为

式中，ρ 为10min的平均空气密度；P为10min测量的干燥空气平均气压；R0为干燥空气的气体系数，取R0=287.05J/(kg·K)；T为10min的平均测量温度，计算时取T=TC+273.15，TC为实际温度。图5给出了不同气压下温度与空气密度的关系。

图5 温度与空气密度函数关系Fig.5 Air density as function of temperature

图5可以看出，气压越低，空气密度越小，且随着温度增大，空气密度将变小。

2）湿度与空气密度的数学模型

非干燥空气时，基于特滕斯公式（Tetens Formula）的饱和水蒸气压力为

式中，C0、C1、C2分别为特滕斯公式的系数，C0= 6.107 8，C1=7.5，C2=237.3。

相对湿度定义为实际水蒸气压力和饱和水蒸气压力的比值，记为PH%。实际水蒸气压力为考虑湿度的空气密度计算公式为

图6给出了相对湿度与空气密度的关系。

图6 相对湿度和温度与空气密度函数关系Fig.6 Air density as function of relative humidity and temperature

图6可以看出，随着相对湿度变大，空气密度将变小。但在温度较低时，相对湿度分别为0%和100%的空气密度数值差别不大，此时相对湿度对空气密度影响不大，而在夏天气温较高时，则需要计及相对湿度的影响。例如40℃时，PH=0干燥条件下空气密度为1.127 2kg/m3，PH=100潮湿条件下空气密度为1.096 2kg/m3。本文给出高于30℃时需要计及相对湿度的影响，30℃是经验值或预设值，30℃的选取与计算精度有关，当计算精度需求较高时，取低于30℃的数值。当计算精度需求较低时，取高于30℃的数值。

综上所述，温度和湿度变化后，将引起空气密度的变化，风机最优功率曲线将会改变，接下来推导计及温度和湿度的PSF算法。

2 考虑温度和湿度的PSF算法

计及温度和湿度的PSF算法，首先需要给出标准大气压和标准温度下（即标准空气密度）的ω -P最优功率曲线，然后计算计及温度和湿度的空气密度，并对ω

-P最优功率曲线进行修正。

2.1 标准空气密度下的最优功率曲线

标准气压为101 325Pa，标准空气密度为1.225kg/m3，由式（1）可得标准空气密度下ω -P的关系为

式中，ρ0为标准空气密度，取1.225kg/m3；K0为系数。ω

-P关系的标幺值表达形式为

式中，“*”为标幺值；n*ω为额定机械转速，n*ω= 1.1(pu)。

文献[17,18]指出由于存在风电机组的机械损耗、定子铜耗、转子铜耗、磁心损耗、变频器损耗等，最大功率运行点可能会漂移，由于运行点漂移方向和大小与风速、转速以及控制策略等有关，且不固定，因此给出一种实验或仿真获得最优功率曲线的方法。其步骤如下：

（1）首先根据风力机风能利用系数与叶尖速比的数学关系确定最优叶尖速比（即风能利用系数最大时对应的叶尖速比）。

（2）通过实验或仿真，分别输入风速5m/s, 6m/s, …, 12m/s，改变ω -P最优功率曲线的参考有功功率，观察叶尖速比。

（3）叶尖速比等于最优叶尖速比时记录此时的转速和参考有功功率。

（4）插值法等量分配ω -P最优功率曲线的各控制点。

2.2 考虑温度和湿度的最优功率曲线

根据前述原理，当温度和湿度发生变化，空气密度会变化，需要对基于标准空气密度的最优功率曲线进行修正，设修正系数为K。当温度小于等于30℃时，不考虑湿度的影响，把式（3）代入式（4）可求取空气密度，空气密度相除可得修正系数的计算公式为

根据1.3节，当温度大于30℃时，需同时考虑温度和湿度的影响，把式（5）和式（6）代入式（7）可求取空气密度，空气密度相除可得修正系数的计算公式为

通过式（10）或式（11）计算修正系数，并把修正系数乘以2.1节获得标准空气密度下最优功率曲线的参考有功功率，修正后最优功率曲线的参考有功功率如果大于1，则取1，其表达式为

考虑温度和相对湿度的PSF算法如图7所示。

图7 考虑温度和相对湿度的PSF算法Fig.7 PSF algorithm considering temperature and relative humidity

3 考虑温度和湿度PSF算法的实施过程

考虑温度和湿度PSF算法实施步骤如下：

（1）根据2.1节的方法，通过实验或仿真得到标准空气密度下的最优功率曲线。

（2）根据气象资料或安装传感器实时得到机舱外温度和相对湿度，结合风机的海拔高度，代入修正系数计算公式。

（3）当温度小于等于30℃时，利用式（10）计算修正系数；当温度大于30℃时，利用式（11）计算修正系数。

（4）利用式（12）计算修订后的最优功率曲线的参考有功功率。

（5）根据参考有功功率计算风机电磁力矩参考值，进而计算D轴转子电流参考值，输入变频器进行风机控制。

具体实施时需要考虑传感器的检测误差和避免空气密度变化的频繁动作，为此给出的流程如图8所示。

4 仿真证明与风机测试

4.1 仿真测试系统及参数

为证明提出方法，在Matlab/Simulink中建立了仿真算例，其结构示意图如图9所示。该风电场由100台2MW双馈风电机组组成，假定机组感受相同的风速，采用一台等值风电机组表征风电场模型，风电机组经机端负荷和变压器T1（110kV/690V）连接到外部电网，等值风机的容量为200MW，等值风机的参数见表1。

4.2 算例1

为了验证2.1节提出的利用实验和仿真方法获取标准空气密度的最优功率曲线方法，首先确定最优叶尖速比。假定桨距角为0，根据风力机特性，风能利用系数与叶尖速比的关系为

图8 考虑温度和相对湿度的PSF算法流程Fig.8 Flow chat of PSF algorithm considering temperature and relative humidity

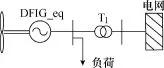
图9 双馈机组风电场系统单线示意图Fig.9 Single line diagram of wind farm of DFIG

表1 等值机电气参数Tab.1 Electric parameters of equivalence turbine

根据式（13），可以得到风能利用系数取得最大值时最优叶尖速比为8.1。然后通过仿真方法和最优叶尖速比，得到标准空气密度的最优功率曲线，搭建相应的PSF仿真模型。并与式（8）原有方法得出最优功率曲线搭建的风机模型进行仿真对比。

图10是输入风速，图11和图12给出了两种方法的风机叶尖速比和风能利用系数的特性曲线。

图10 算例1风速Fig.10 Wind speed in example 1

图11 算例1叶尖速比Fig.11 Tip-speed ratio in example 1

图12 算例1风能利用系数Fig.12 Power coefficient in example 1

从图11可以看出，无论风速在8m/s还是9m/s，采用本文方法的风机叶尖速比都在8.1左右，该方法优于原有方法。从图12的风能利用系数可以看出相同的结论，从而证实了考虑风机实际损耗的方法将取得更高的风能利用效率。当然本文算例模型只是考虑了定子和转子铜耗，可以预计，如果把所有损耗都考虑，本文方法将会体现更大的优越性。

4.3 算例2

为验证温度对PSF算法的影响，根据2.2节式（10）搭建基于考虑温度的PSF算法的风机模型和不考虑温度的PSF算法的风机模型。假定温度为-33℃，根据式（4）可知此时空气密度为1.47kg/m3。图13为输入风速，图14和图15分别为两种模型的风机风能利用系数和输出功率特性曲线。

图13 算例2风速Fig.13 Wind speed in example 2

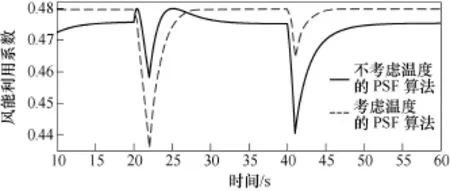
图14 算例2风能利用系数Fig.14 Performance coefficient of wind energy in example 2

图15 算例2风机输出功率Fig.15 Output power of wind turbine in example 2

从图14可以看出，考虑温度的PSF算法与不考虑温度的PSF算法相比，其风能利用系数有较大的提高。注意到，风速从7m/s升到9m/s的过程中，由于机组惯性的原因，不考虑温度的PSF算法略好，但风速从9m/s降到8m/s的过程中，考虑温度的PSF算法相对获得更大的风能利用系数。为分析原因，给出风机转子运动方式，即

式中，Tm为风机输入的气动力矩；Te为风机输出的电磁力矩；ΔT为风机力矩差；H为风机惯性时间常数；ω 为风机转速。

当风速增加时，风机加速，根据图2风机将从一个最优控制点过渡到另一个最优控制点，如风机转速加速越快，则其风能利用系数越优。从式（14）可以看出，力矩差越大，风机转速加速越快。从图15可以看出，相比不考虑温度PSF算法的情况，20s时考虑温度PSF算法的输出功率较大，即式（14）中Te较大，风速增加后两种情况的Tmd的增加几乎相同，由于风机惯性，电磁力矩Te保持不变，因此考虑温度PSF算法的ΔT小于不考虑温度PSF算法的ΔT，考虑温度PSF算法的转速加速效果相对较差，这就是风速从7m/s升到9m/s的过程中考虑温度PSF算法的风能利用系数相对较差的原因。同理风速从9m/s降到8m/s过程中，考虑温度的PSF算法的ΔT绝对值较大，其转速跟踪特性更好，因此考虑温度的PSF算法的风能利用系数相对较好。总体来看，考虑温度的PSF算法建立的模型比不考虑温度的PSF算法获得了更高的风能转换效率。

4.4 算例3

为验证高温时计及空气湿度对PSF算法的影响，根据2.2节式（12）搭建基于考虑温度的PSF算法的风机模型和仅考虑温度的PSF的风机模型。根据图4，当温度为40℃时，相对湿度为0时空气密度为1.127 2kg/m3，相对湿度为100%时标准空气密度为1.096 2kg/m3。图16为输入风速，图17和图18分别出给了两种模型的风机叶尖速比和风能利用系数的特性曲线。

图16 算例3风速Fig.16 Wind speed in example 3

图17 算例3叶尖速比Fig.17 Tip-speed ratio in example 3

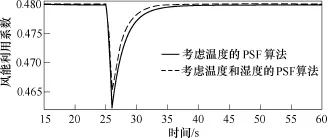
图18 算例3风能利用系数Fig.18 Power coefficient in example 3

从图17可以看出，考虑温度和湿度的FSF算法模型比仅考虑温度的FSF算法模型得到更接近8.1的最优叶尖速比。从图18可以看出，考虑温度和湿度的FSF算法建立的模型优于仅考虑温度的FSF算法建立的模型，说明当温度较大时需要考虑相对湿度的影响。本文30℃是经验值或预设值，该值与计算精度有关，并可根据计算精度进行调整。

4.5 风电场测试

为验证方法的有效性，项目合作单位许继集团有限公司的许昌许继风电科技有限公司已将该方法应用到风机MPPT的实际控制中，并正在国家风光储输（张北）示范风电场进行测试，为简化测试，利用式（4）测得空气密度，并用式（10）进行风机的控制。目前已完成阶段测试，测试风机为风电场第14号机组，是许昌许继风电科技有限公司生产的2MW双馈风电机组，测试共分两个阶段：第一阶段测试时间为2016年2月29日到2016年11月22日，风机采用原有MPPT控制方法；第二阶段测试时间为2016年11月23日到2017年3月2日。测试的温度条件是-10℃～0℃，测试的相对湿度为25%～35%。测试中由于风机高度不变，风机的气压基本不变，因此不需要测试气压。另外，由于测试气温较低，湿度对空气密度的影响较小，因此在该情况下只需测量温度即可。风机采用本文提出的MPPT控制方法，通过数理统计分别绘制出对应的风机功率曲线，如图19所示。该功率曲线由中国电力科学研究院绘制，功率曲线已经折算到标准空气密度下。

图19 风机测试的功率曲线对比Fig.19 Comparison of power curves for wind turbine test

从图19可以看出，采用本文提出的MPPT控制方法获得的风机功率曲线优于采用原有MPPT控制方法获得的风机功率曲线，特别在风速为8～12m/s该优势更加明显，从而证实了该方法的有效性。另外，图中高风区有一个点明显偏低，其原因是该区间得到的数据集数目较少以及该机组的特殊运行工况。从整体来看，本文提出的MPPT方法明显优于原有方法。

5 结论

1）给出温度和湿度与空气密度的数学关系，分析了温度和湿度影响PSF算法的机理。给出了考虑温度和湿度的PSF算法。

2）由于机组损耗的存在，采用实验或仿真的方法获取标准空气密度的最优功率曲线来控制风机将比原有方法获得更大的风能利用效率。

3）考虑温度和湿度的PSF算法将获得更大的风能转换效率。当温度较低时，不用计及湿度对PSF算法的影响，仅需考虑温度对PSF算法的影响；当温度较高时，需要计及相对湿度对空气密度的影响，此时PSF算法需要同时考虑温度和湿度的影响。

[1] Dipesh Kumar, Kalyan Chatterjee. A review of conventional and advanced MPPT algorithms for wind energy systems[J]. Renewable and Sustainable Energy Reviews, 2016, 55： 957-970.

[2] Wang Q, Chang L. An intelligent maximum power extraction algorithm for inverter-based variable speed wind turbine systems[J]. IEEE Transactions on Power Electronics, 2004, 19(5)： 1242-1249.

[3] Kazmi S M R, Goto H, Guo H J, et al. A novel algorithm for fast and efficient speed-sensorless maximum power point tracking in wind energy conversion systems[J]. IEEE Transactions on Industrial Electronics, 2011, 58(1)： 29-36.

[4] 殷明慧, 张小莲, 邹云, 等. 跟踪区间优化的风力机最大功率点跟踪控制[J]. 电网技术, 2014, 38(8)：2180-2185. Yin Minghui, Zhang Xiaolian, Zou Yun, et al. Improved MPPT control of wind turbines based on optimization of tracking range[J]. Power System Technology, 2014, 38(8)： 2180-2185.

[5] 贾锋, 李征, 蔡旭. 提高大型风电机组恒转速段发电量的变桨策略[J]. 电工技术学报, 2017, 32(1)： 58-68. Jia Feng, Li Zheng, Cai Xu. Advanced pitch control for improving power production for large scale wind energy conversion system under constant speed region[J]. Transactions of China Electrotechnical Society, 2017, 32(1)： 58-68.

[6] 马祎炜, 俞俊杰, 吴国祥, 等. 双馈风力发电系统最大功率点跟踪控制策略[J]. 电工技术学报, 2009, 24(4)： 202-208. Ma Yiwei, Yu Junjie, Wu Guoxiang, et al. MPPT control strategy for doubly-fed wind power generation[J]. Transactions of China Electrotechnical Society, 2009, 24(4)： 202-208.

[7] 田兵, 赵克, 孙东阳, 等. 改进型变步长最大功率跟踪算法在风力发电系统中的应用[J]. 电工技术学报, 2016, 31(6)： 226-233. Tian Bing, Zhao Ke, Sun Dongyang, et al. Promoted variable step maximum power point tracking algorithm used in the wind energy conversion system[J]. Transactions of China Electrotechnical Society, 2016, 31(6)： 226-233.

[8] 张凤阁, 朱连成, 金石, 等. 开绕组无刷双馈风力发电机最大功率点跟踪直接转矩模糊控制研究[J].电工技术学报, 2016, 31(15)： 43-53. Zhang Fengge, Zhu Liancheng, Jin Shi, et al. Research on the maximum power point tracking of brushless doubly-fed wind power generator with open winding direct torque fuzzy control strategy[J]. Transactions of China Electrotechnical Society, 2016, 31(15)： 43-53.

[9] 李咸善, 徐浩, 杜于龙. 采用叶尖速比法和爬山搜索法相结合的风力发电系统最大功率点跟踪研究[J]. 电力系统保护与控制, 2015, 43(13)： 66-71. Li Xianshan, Xu Hao, Du Yulong. Maximum power tracking of wind power generation system using the combination of tip speed ratio method and climbing search method[J]. Power System Protection and Control, 2015, 43(13)： 66-71.

[10] 刘丹, 李强, 冯承超. 小型直驱式永磁同步风力发电机快速最大功率追踪仿真研究[J]. 电力系统保护与控制, 2016, 44(5)： 141-145. Liu Dan, Li Qiang, Feng Chengchao. A simulation study of small direct drive type permanent magnet synchronous generator fast maximum power tracking[J]. Power System Protection and Control, 2016, 44(5)： 141-145.

[11] 吴爱华, 赵不贿, 茅靖峰, 等. 基于转矩观测器的垂直轴风力发电最大功率跟踪反演控制[J]. 电力系统保护与控制, 2017, 45(2)： 7-13. Wu Aihua, Zhao Buhui, Mao Jingfeng, et al. Back-stepping control for vertical axis wind power generation system maximum power point trackingbased on torque observer[J]. Power System Protection and Control, 2017, 45(2)： 7-13.

[12] 瞿萍, 朱明, 魏明星, 等. 垂直轴直驱永磁同步风力发电机的滑模控制设计[J]. 电气技术, 2014, 15(6)： 5-9. Qu Ping, Zhu Ming, Wei Mingxing, et al. Sliding mode controller for vertical axis permanent magnet direct drive wind power generation system[J]. Electrical Engineering, 2014, 15(6)： 5-9.

[13] 张小莲, 李群, 殷明慧, 等. 一种引入停止机制的改进爬山算法[J]. 中国电机工程学报, 2012, 32(14)：128-134. Zhang Xiaolian, Li Qun, Yin Minghui, et al. An improved hill-climbing searching method based on halt mechanism[J]. Proceedings of the CSEE, 2012, 32(14)： 128-134.

[14] 陈家伟, 陈杰, 龚春英. 变速风力发电机组恒带宽最大功率跟踪控制策略[J]. 中国电机工程学报, 2012, 32(27)： 32-38. Chen Jiawei, Chen Jie, Gong Chunying. A constantbandwidth MPPT strategy for variable-speed WECS[J]. Proceedings of the CSEE, 2012, 32(27)： 32-38.

[15] 张小莲, 殷明慧, 周连俊, 等. 风电机组最大功率点跟踪控制的影响因素分析[J]. 电力系统自动化, 2013, 37(22)： 15-21. Zhang Xiaolian, Yin Minghui, Zhou Lianjun, et al. Analysis on factors affecting performance of MPPT control[J]. Automation of Electric Power Systems, 2013, 37(22)： 15-21.

[16] 楚峥, 李楠. 自适应空气密度变化的风电机组最优转矩控制[J]. 上海电气技术, 2014, 7(2)： 41-44. Chu Zheng, Li Nan. Air density self-adapting wind turbine optimal torque control[J]. Journal of Shanghai Electric Technology, 2014, 7(2)： 41-44.

[17] 胡家兵, 贺益康, 刘其辉. 基于最佳功率给定的最大风能追踪控制策略[J]. 电力系统自动化, 2005, 29(24)： 32-38. Hu Jiabing, He Yikang, Liu Qihui. Optimized active power reference based maximum wind energy tracking control strategy[J]. Automation of Electric Power Systems, 2005, 29(24)： 32-38.

[18] De Kooning J D M, Vandoorn T L, de Vyver J V, et al. Displacement of the maximum power point caused by losses in wind turbine systems[J]. Renewable Energy, 2016, 85： 273-280.

（编辑 郭丽军）

Maximum Power Point Tracking Control of Wind Turbine Considering Temperature and Humidity

Su Xunwen1,2Xu Dianguo2Yang Rongfeng2Yue Hongxuan3
（1. Institute of Electrical and Control Engineering Heilongjiang University of Science and Technology Harbin 150027 China 2. Institute of Electrical Engineering and Automation Harbin Institute of Technology Harbin 150001 China 3. Xu Ji Group Corporation Xuchang 461000 China）

In order to study the effects of environmental factors on maximum power point tracking (MPPT) control of wind turbine, taken power signal feedback algorithm as an example, the mechanism of temperature and humidity affecting PSF algorithm is analyzed based on mathematical relationships of temperature and humidity with air density. Then this paper presents the method for the optimal power curve acquisition, the implementation process and flow chat of PSF algorithm considering temperature and humidity. The influence of loss of wind turbine is considered in this PSF algorithm. The models with doubly fed induction generator wind turbines based PSF algorithm are built on Matlab/Simulink platform. At last, the simulation results and field test in wind farm show that the PSF algorithm considering temperature and humidity can obtain high wind energy conversion efficiency.

Temperature, humidity, power signal feedback algorithm, wind turbine, maximum power curve

TM614

苏勋文 男，1976年生，博士后，研究方向为风电场建模与验证,风力发电对电力系统的影响。

E-mail： suxunwen@163.com（通信作者）

徐殿国 男，1960年生，教授，博士生导师，研究方向为电力电子技术、照明电子技术。

E-mail： xudiang@hit.edu.cn

10.19595/j.cnki.1000-6753.tces.170480

国家电网公司科技项目资助（SGSDDK00KJJS1500155），国家自然科学基金重点项目（51237002），国家自然科学基金（51677057），哈尔滨市科技创新人才研究专项资金（青年后备）项目（RC2015QN007019），博士后研究人员落户黑龙江科研启动项目（LBH-Q15125）资助。

2017-04-20 改稿日期 2017-05-05