偏心条件下轴向磁通轮毂电机不平衡弯矩建模与分析

邓文哲 左曙光 林 福 吴双龙 毛 钰

（同济大学新能源汽车工程中心 上海 201804）

偏心条件下轴向磁通轮毂电机不平衡弯矩建模与分析

邓文哲 左曙光 林 福 吴双龙 毛 钰

（同济大学新能源汽车工程中心 上海 201804）

为了分析静态偏心和动态偏心对轴向磁通轮毂电机的影响，首先建立了未偏心时轴向磁通电机气隙磁场的准3D解析模型，该模型分别通过复数相对气隙磁导和径向修正函数考虑了开槽和边缘效应对气隙磁场的影响；然后通过分析静态偏心和动态偏心时气隙长度随时间和空间的变化，建立了偏心条件下轴向磁通电机的气隙磁场解析模型，有限元结果表明该模型可以准确预测偏心条件下任意位置的气隙磁通密度；最后根据该模型分析了偏心对轴向电机气隙磁场和电磁力的影响，提出了计算不平衡弯矩的方法。结果表明：不同于径向电机，偏心除了产生不平衡磁拉力，还会使轴向磁通电机产生与旋转方向正交的弯矩，该弯矩有导致偏心进一步加剧的趋势。

轴向磁通轮毂电机 静态偏心 动态偏心 解析模型 弯矩

0 引言

分布式驱动电动汽车以其特有的结构及性能优势成为未来汽车发展的方向[1]。轴向磁通永磁同步电机也被称为盘式电机，由于其结构紧凑、轴向长度小、功率密度高，作为轮毂电机使用具有非常广阔的应用前景[2-4]。然而由于轮毂电机经常工作在起动、加速、制动等各种复杂工况下，制造装配过程中的误差、运行过程中受到的外力冲击以及定、转子质量的不平衡等多种因素都会引起轴向磁通电机的定、转子轴线不再重合，从而产生偏心。轴向磁通电机发生偏心时不仅气隙磁场发生畸变，谐波成分增加，恶化电机性能，严重时还会导致定、转子相互摩擦，电机损坏。

偏心对径向电机气隙磁场和电磁力的影响已经得到了广泛的研究[5-9]。径向电机发生偏心时，其径向力波的空间阶数和频率特性均会发生变化，从而增加电机发生共振的可能性。同时偏心产生的不平衡磁拉力会导致轴承受力增加，加剧轴承磨损。和径向电机相比，由于结构存在着差异，轴向电机发生偏心时呈现出新的特点。文献[10]通过解析法分析了静态偏心对轴向磁通电机气隙磁场的影响，但在建模时忽略了边缘效应的影响。文献[11]通过有限元法分析了静态偏心系数对轴向磁通电机气隙磁通密度和感应电动势的影响，指出静态偏心下轴向磁通电机会受到恒定的弯矩，该方法可以准确计算偏心下的气隙磁场，但由于必须采用三维有限元法，十分耗时，并且在计算弯矩时采用了集中力的方法，忽略了电磁力的分布特性。文献[12,13]提出了通过测量空间上均匀分布的三个线圈的反电动势对轴向电机进行静态偏心诊断，该方法可以诊断出静态偏心量，但由于需要在制造时引入额外的线圈，不具有普适性。综合上述文献可知，目前关于轴向磁通电机偏心的研究相对较少，且主要关注的焦点在于静态偏心，未涉及动态偏心对轴向磁通电机的影响。有限元法可以准确计算轴向磁通电机的气隙磁场分布，但其结构决定了必须采用十分耗时的三维有限元法，因此需要建立一种快速有效的方法来分析不同偏心形式对轴向磁通电机的影响。

本文以一台30极27槽轴向磁通轮毂电机（Axial-Flux in-Wheel Motor, AFWM）为例，首先建立了未偏心时的气隙磁场准3D解析模型，该模型通过复数相对气隙磁导和径向修正函数考虑了开槽和边缘效应对气隙磁场的影响；接着通过分析轴向磁通电机发生静态偏心和动态偏心时气隙长度随时间和空间的变化，建立了偏心条件下的气隙磁场解析模型，有限元结果表明该模型可以准确预测偏心条件下任意位置的气隙磁通密度；最后根据该模型分析了偏心对轴向磁通电机的影响，提出了计算不平衡弯矩的方法。

1 轴向磁通轮毂电机结构

本文的研究对象为某一轴向磁通轮毂电机，该电机具有外转子结构，永磁体为扇形结构，采用分数槽集中绕组，定子通过定子托盘固定在轴上，转子盘、永磁体、机壳和端盖构成外转子系统，外转子通过轴承和周向分布的六个螺栓分别与轴和轮毂相连，如图1所示。

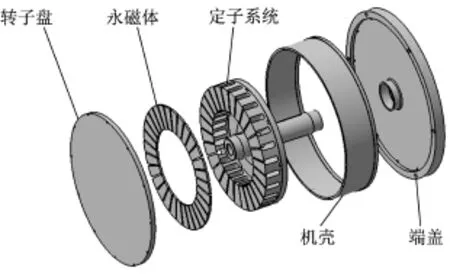
图1 轴向磁通轮毂电机爆炸图Fig.1 Exploded view of AFWM

该轴向磁通轮毂电机的主要参数见表1。

表1 轴向磁通轮毂电机主要参数Tab.1 Main parameters of AFWM

2 未偏心时气隙磁场准3D模型

为了建立未偏心时轴向磁通电机的气隙磁场解析模型，计算了未开槽时的永磁体气隙磁场，通过复数相对气隙磁导考虑了开槽的影响，通过径向修正函数考虑了边缘效应对气隙磁场的影响。

2.1 无齿槽气隙磁场

对于实际开槽的电机，应首先计算未开槽时的气隙磁通密度。将轴向磁通电机沿着永磁体不同半径位置展开，则其气隙磁场可以等效成不同直线电机的叠加，如图2所示，其中z向和θ 向分别表示轴向磁通电机的轴向和周向。

图2 等效模型Fig.2 Equivalent model

假设：①定、转子铁心磁导率无穷大；②忽略漏磁和饱和的影响。则其气隙磁场轴向和切向分量分别表示为

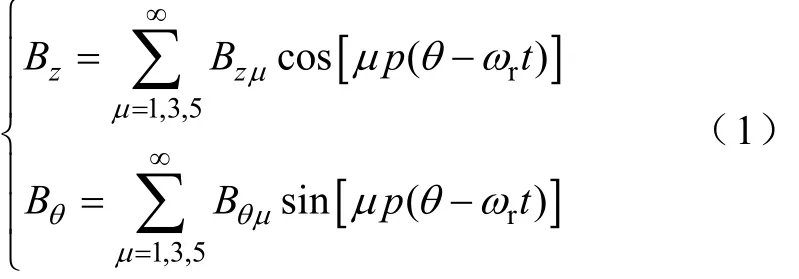
气隙中各阶磁通密度表达式为

其中

式中，Br为永磁体剩磁；αp为永磁体极弧系数；hm为永磁体厚度；g为气隙长度，0g为未发生偏心时的气隙长度；L为定、转子之间的距离；z为求解位置到转子的轴向距离；rω为旋转角频率；p为极对数；R为永磁体半径。

2.2 复数相对气隙磁导

文献[14]采用相对气隙磁导来考虑开槽对气隙磁场的影响，但由于其忽略了切向磁导的影响导致该方法对于切向磁场求解精度较差。复数相对气隙磁导很好地弥补了这一缺陷，可以准确计算法向和切向气隙磁场[15]。

复数相对气隙磁导可以表示为

实部和虚部可以表示成傅里叶级数的形式，即

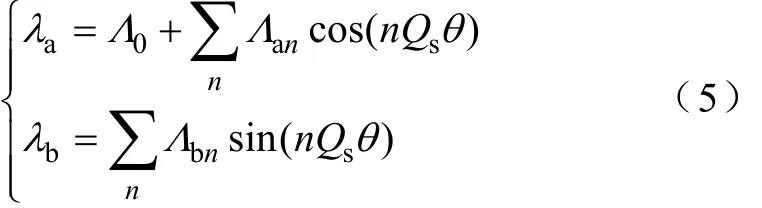
对于该轴向磁通轮毂电机，其平均半径处沿着圆周方向复数相对气隙磁导的实部和虚部如图3所示。

图3 相对气隙磁导Fig.3 Relative air-gap permeance

2.3 有齿槽气隙磁场

为考虑开槽对气隙磁场的影响，将复数相对气隙磁导引入无齿槽气隙磁场中，可以得到实际开槽情况下的气隙磁通密度为

Bslot实部和虚部分别为轴向磁通密度和切向磁通密度，即

2.4 边缘效应修正系数

图4为该电机的轴向磁通密度的空间分布。从图4中可以看出，由于该轮毂电机的永磁体为扇形，不同半径处极弧系数相等，因此沿着径向气隙磁通密度几乎不发生变化，而在内、外径处由于边缘效应的影响，气隙磁通密度呈现出较大的下降趋势，因此在建模时需要考虑边缘效应带来的影响。为了表示这种磁通密度的径向依赖性，本文引入修正函数()GR来考虑边缘效应的影响[16]。

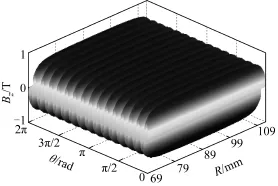
图4 未偏心时气隙磁通密度空间分布Fig.4 Spatial distribution of air gap density without eccentricity

式中，1R和2R分别为永磁体的内径和外径；β用来修正永磁体内、外径处磁通密度的下降速度，其值可以通过参数化有限元分析得到。修正函数G(R)沿半径方向的分布如图5所示，在平均半径处G(R)值为1，而在内、外半径处G(R)值出现了较大下降，约为0.55。

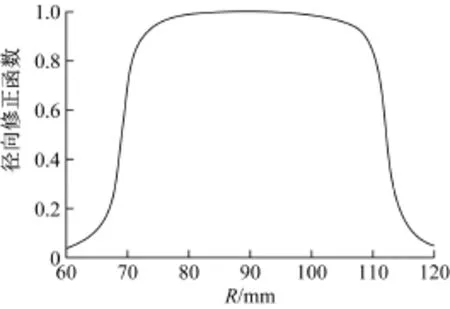
图5 边缘效应修正函数Fig.5 Correction function of fringing effect

因此，考虑边缘效应的轴向和切向气隙磁通密度可以表示为

根据式（1）、式（5）、式（7）和式（9），可以得到未偏心时轴向磁通电机的气隙磁通密度。由式（9）可以看出，轴向磁通电机的气隙磁通密度不仅和空间角度、时间有关，同时也受到其径向位置的影响。

3 偏心条件下气隙磁场建模

对于轴向磁通电机而言，偏心同样可以分为静态偏心、动态偏心和混合偏心。轴向磁通电机发生静态偏心时定子与转子的轴线发生了偏移，但转子的轴线与转轴仍然重合，如图6所示。此时气隙沿圆周方向不再均匀，但任意位置处的气隙长度不随时间发生变化，即最小气隙的位置不随时间发生变化。当轴向磁通电机发生动态偏心时，定子与转子的轴线发生了偏移，但此时转轴与定子的轴向重合，此时气隙长度不仅在空间上不再均匀，最小气隙位置还会随时间发生周期性变化。混合偏心是指同时存在静态偏心和动态偏心的情况。

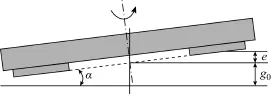
图6 静态偏心示意图Fig.6 Schematic diagram of static eccentricity

3.1 静态偏心

类比于径向电机，定义静态偏心系数为

式中，e为平均半径处气隙长度最大变化量。

根据式（10）可以得到不同偏心系数下转子的偏转角度，见表2。由表2可以看出，非常小的偏转角度可以导致较大的偏心系数，当偏心系数达到40%时，转子偏转角度仅有0.379 9°，因此对于轮毂电机而言，由于其经常工作在各种复杂工况下，定、转子容易受到冲击，再加上制造装配误差等因素的影响，非常易于产生偏心。

表2 不同偏心系数下转子偏转角度Tab.2 Incline angle with different eccentricity ratio

当轴向磁通电机发生静态偏心时，平均半径处沿圆周方向的气隙长度可以表示为

式中，0γ为最小气隙位置。

由于轴向电机定、转子轴线发生了偏移，不同半径处的气隙长度将不再相等。根据式（11）和图6，任意半径处的气隙长度为

式中，R为求解半径；Rm为平均半径，Rm=(R1+R2)/2。

此时，气隙长度不仅沿圆周方向不再均匀，沿径向也会发生变化，且越靠近外径处变化程度越大，如图7所示。

图7 静态偏心下气隙长度Fig.7 Air gap length with static eccentricity

将式（12）代入式（9）中即可得到静态偏心下轴向磁通电机的气隙磁场解析模型。该模型的准确性通过图8所示的有限元模型进行了验证，在计算时假定转子绕x轴发生了偏转，则γ090=◦。分别选取平均半径处气隙磁通密度在0t=时刻的空间分布和0θ=◦位置处的时间历程进行了对比，如图9所示，解析计算结果和有限元结果吻合较好。由图9a可知，在0°～180°范围内，气隙长度相较于初始值有所下降，导致磁通密度幅值增加，180°～360°范围内，气隙长度增加，磁通密度幅值出现了下降。由于任意位置的气隙长度不随时间发生变化，因此其磁通密度的幅值不随时间发生变化，如图9b所示。图10为静态偏心下气隙磁通密度沿径向和周向的空间分布。可以看出在静态偏心下气隙磁通密度发生了畸变，且越靠近外径处，畸变程度越大，其畸变程度与气隙的变化量呈正比。同时在内、外径处由于边缘效应的影响气隙磁通密度幅值出现了较大下降。

图8 轴向磁通电机有限元模型Fig.8 Finite element model of AFWM

3.2 动态偏心

与静态偏心类似，定义动态偏心系数为

图9 静态偏心下气隙磁通密度解析与有限元对比Fig.9 Comparison of air gap density predicted by analytical and FE method with static eccentricity

图10 静态偏心下气隙磁通密度空间分布Fig.10 Spatial distribution of air gap density with static eccentricity

动态偏心系数对应的偏转角与静态偏心相等，不同之处在于其偏转方向随时间发生变化，因此平均半径处沿圆周方向气隙长度可以表示为

动态偏心示意图如图11所示。根据式（14）和图11，任意半径处的气隙长度可以表示为

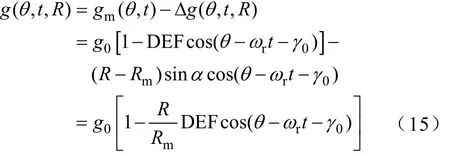
图11 动态偏心示意图Fig.11 Schematic diagram of dynamic eccentricity

与式（12）相比，式（15）中引入了时间项，气隙长度将随时间发生周期性变化。将式（15）代入式（9）中即可得到动态偏心下轴向磁通电机的气隙磁场解析模型。动态偏心下该模型的准确性同样通过图8所示的有限元模型进行了验证。分别选取了平均半径处气隙磁通密度在0t=时刻的空间分布和0θ=◦位置处的时间历程进行了对比，如图12所示，解析计算结果和有限元结果吻合较好。由图12a可知，0t=时刻在0°～180°范围内，气隙长度相较于初始值有所下降，导致磁通密度幅值增加，180°～360°范围内，气隙长度增加，磁通密度幅值出现了下降。由于动态偏心下气隙长度随时间发生周期性变化，其磁通密度幅值随时间也会发生变化，对于该监测点而言，前半个周期内气隙长度降低，磁通密度幅值有所增加，后半个周期气隙长度增加，磁通密度幅值出现了下降，如图12b所示。因此动态偏心下气隙磁通密度幅值不仅沿径向和周向发生了变化，随时间也会发生周期性的改变。

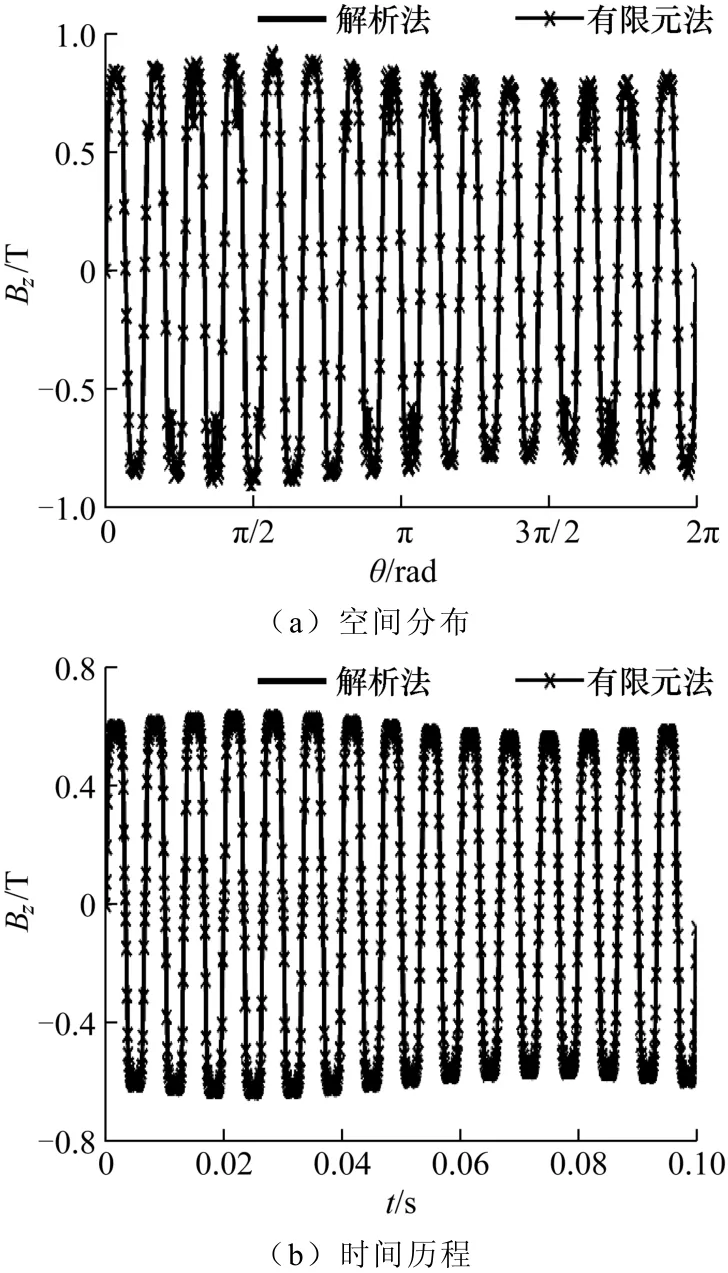
图12 动态偏心下气隙磁通密度解析与有限元对比Fig.12 Comparison of air gap density predicted by analytical and FE method with dynatic eccentricity

4 偏心对轴向磁通电机影响分析

径向电机发生偏心后，其径向力波的空间阶数和频率特性均会发生变化。与径向电机类似，对于轴向磁通电机而言，偏心同样会导致轴向力波的空间阶数和频率特性发生变化。静态偏心会导致轴向力波的空间阶次产生1±、2±阶成分，动态偏心不仅会导致轴向力波的空间阶次产生1±、2±阶成分，还会在原有频率的基础上增加1±、2±倍转频成分。这些额外的成分会增加电机共振的可能性，导致其振动与噪声特性恶化。然而与径向电机相比，由于结构存在着差异，轴向电机发生偏心时呈现出一些新的特点。

轴向磁通电机未发生偏心时，其受到的轴向力波沿圆周方向均匀分布。发生偏心后，沿圆周方向轴向力不再均匀分布，气隙减小的位置轴向力幅值增大，气隙变大的位置轴向力幅值降低，如图13所示。不平衡的电磁力会导致定子和转子分别受到额外的弯矩作用，根据右手定则，该弯矩的方向始终指向气隙不变的位置，且与旋转方向正交。

图13 未偏心和偏心条件下不平衡磁拉力示意图Fig.13 Schematic diagram of unbalanced magnetic pull with and without eccentricity

该弯矩的大小可以通过图14所示弯矩求解模型进行求解。根据麦克斯韦张量法，轴向力波为

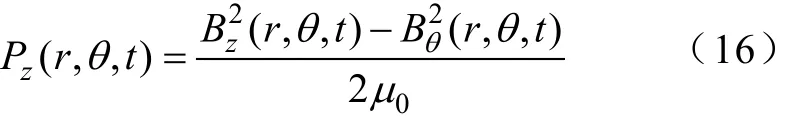
则图14中每个微元受到的电磁力为

该微元关于x轴和y轴产生的弯矩分别表示为

图14 弯矩求解模型Fig.14 Caculation model of bending moment

将dMx和dMy沿径向和周向进行积分，即可得到定子和转子关于x轴和y轴的弯矩分别为

轴向磁通电机未发生偏心时，其轴向力波关于x轴和y轴对称，因此其关于x轴和y轴的弯矩也等于零。当轴向电机发生静态偏心和动态偏心后，由于气隙磁场发生畸变，轴向力波不再对称，式（19）将不再等于零。

4.1 静态偏心

根据式（19）对静态偏心下的电磁力进行积分可以得到不同静态偏心系数下定、转子关于x轴和y轴的弯矩，计算结果如图15所示。在计算时假定转子绕x轴发生了偏转，由于气隙长度不随时间发生变化，因此在静态偏心下只存在关于x轴的弯矩，关于y轴的弯矩等于零。该弯矩几乎不随时间发生波动，其均值与静态偏心系数呈正比，如图16所示。有限元与解析结果相一致，证明了本文弯矩计算方法的有效性。该弯矩会使轴承受到恒定的反作用力，当定子系统刚度较小时，有进一步加剧偏心的趋势。同时由图16可以看出，当偏心系数为10%时，定子会受到13.56N·m的弯矩，这说明微小的偏心就会导致定子受到较大的弯矩，在轮毂电机设计时需要保证定子系统具有较大的刚度来抵抗运行过程中可能产生的由偏心导致的额外弯矩。

图15 静态偏心下定子关于x和y轴的弯矩Fig.15 Bending moment around x and y axis with static eccentricity

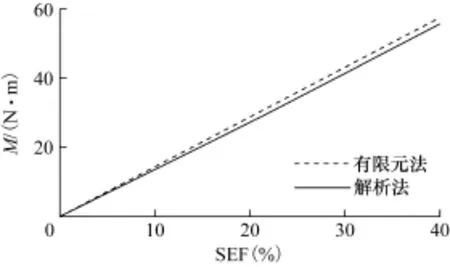
图16 弯矩均值随静态偏心系数变化关系Fig.16 Relationship between mean value of bending moment and static eccentricity factor

4.2 动态偏心

由于动态偏心下气隙长度随时间发生变化，因此气隙不变的位置随时间也相应地不断变化，这就导致动态偏心下产生的弯矩的方向随时间发生周期性变化。同样的，根据式（19）可以得到不同动态偏心系数下定、转子关于x轴和y轴的弯矩，如图17所示。Mx与My分别随时间呈现余弦和正弦变化，其频率等于转频。

图17 动态偏心下定子关于x和y轴的弯矩Fig.17 Bending moment around x and y axis with dynamic eccentricity

合成弯矩为

由图18可知合成弯矩与动态偏心系数呈正比。合成弯矩的均值和静态偏心时相等，但方向会随时间发生周期性变化。根据右手定则，该合成弯矩的方向始终指向气隙不变的位置。由于Mx与My随时间呈现周期性变化，这会导致轴承受到交变的反作用力，从而降低轴承寿命。该弯矩同样有进一步加剧动态偏心的趋势。

图18 弯矩均值随动态偏心系数变化关系Fig.18 Relationship between mean value of bending moment and dynamic eccentricity factor

5 结论

本文首先建立了未偏心下的轴向磁通电机气隙磁场准3D解析模型，该模型通过复数相对气隙磁导和径向修正函数考虑了开槽和边缘效应对气隙磁场的影响。通过分析发生静态偏心和动态偏心后气隙长度随时间和空间的变化，建立了偏心条件下轴向磁通电机气隙磁场模型，并通过有限元模型进行了验证。最后根据该模型分析了偏心对轴向磁通电机的影响，提出了计算不平衡弯矩的方法。主要结论如下：

1）轴向磁通电机发生偏心后气隙磁场会产生畸变。静态偏心时气隙磁通密度在空间上沿径向和周向不再均匀，但其磁通密度幅值不随时间发生变化，发生动态偏心后气隙磁通密度不仅在空间上发生了畸变，其空间分布也将随时间发生周期性的变化。同时不同半径处气隙磁场畸变程度不同，随着半径的增加，气隙磁场的畸变程度越来越大。

2）偏心会使轴向磁通电机的定、转子受到额外的弯矩作用，静态偏心下该弯矩大小和方向保持恒定，动态偏心下该弯矩大小恒定，方向随时间发生周期性变化，始终指向气隙不变的位置。该弯矩导致轴承在静、动态偏心下分别受到恒定和交变的反作用力，降低轴承寿命。当定子系统刚度较小时，有进一步加剧偏心的趋势。

[1] Rahman K M, Patel N R, Ward T G, et al. Application of direct-drive wheel motor for fuel cell electric and hybrid electric vehicle propulsion system[J]. IEEE Transactions on Industry Applications, 2006, 42(5)： 1185-1192.

[2] Giulii C F, De Donato G, Caricchi F. Recent advances in axial-flux permanent-magnet machine technology[J]. IEEE Transactions on Industry Applications, 2012, 48(6)： 2190-2205.

[3] 黄允凯, 周涛, 董剑宁, 等. 轴向永磁电机及其研究发展综述[J]. 中国电机工程学报, 2015, 35(1)：192-205. Huang Yunkai, Zhou Tao, Dong Jianning, et al. An overview on developments and researches of axial flux permanent magnet machines[J]. Proceedings of the CSEE, 2015, 35(1)： 192-205.

[4] Kahourzade S, Mahmoudi A, Ping H W, et al. A comprehensive review of axial-flux permanentmagnet machines[J]. Canadian Journal of Electrical & Computer Engineering, 2014, 37(1)： 19-33.

[5] 左曙光, 张国辉, 吴旭东, 等. 倾斜偏心下轮毂永磁同步电机电磁力分析[J]. 浙江大学学报： 工学版, 2015, 49(5)： 901-907. Zuo Shuguang, Zhang Guohui, Wu Xudong, et al. Analysis of electromagnetic force in wheel-drive PMSM with stator incline eccentricity[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(5)： 901-907.

[6] 鲍晓华, 吕强, 王汉丰. 基于齿部磁场分析的大型潜水电机气隙偏心故障研究[J]. 电工技术学报, 2016, 31(8)： 90-95. Bao Xiaohua, Lü Qiang, Wang Hanfeng. Study on air-gap eccentricity fault in large submersible motors with tooth magnetic field analysis[J]. Transactions of China Electrotechnical Society, 2016, 31(8)： 90-95. [7] Kim D J, Kim H J, Hong J P, et al. Estimation of acoustic noise and vibration in an induction machine considering rotor eccentricity[J]. IEEE Transactions on Magnetics, 2014, 50(50)： 857-860.

[8] 鲍晓华, 李福英, 方勇, 等. 大型潜水电机混合偏心时转子副临界振动的研究[J]. 电工技术学报, 2015, 30(6)： 142-149. Bao Xiaohua, Li Fuying, Fang Yong, et al. Sub-critical speed vibration of rotors for large submersible motors with mixed eccentricity[J]. Transactions of ChinaElectrotechnical Society, 2015, 30(6)： 142-149.

[9] 周晓燕, 章跃进, 李琛, 等. 计及定子开槽的插入式永磁电机转子偏心空载气隙磁场全局解析迭代模型[J]. 电工技术学报, 2014, 29(7)： 66-76. Zhou Xiaoyan, Zhang Yuejin, Li Chen, et al. Opencircuit magnetic field calculation for insert permanent magnet motors with rotor eccentricity based on analytical-iteration method[J]. Transactions of China Electrotechnical Society, 2014, 29(7)： 66-76.

[10] Marignetti F, Vahedi A, Mirimani S M. An analytical approach to eccentricity in axial flux permanent magnet synchronous generators for wind turbines[J]. Electric Power Components and Systems, 2015, 43(8-10)： 1039-1050.

[11] Mirimani S M, Vahedi A, Marignetti F. Effect of inclined static eccentricity fault in single stator-single rotor axial flux permanent magnet machines[J]. IEEE Transactions on Magnetics, 2012, 48(1)： 143-149.

[12] Mirimani S M, Vahedi A, Marignetti F, et al. Static eccentricity fault detection in single-stator-singlerotor axial-flux permanent-magnet machines[J]. IEEE Transactions on Industry Applications, 2012, 48(6)：1838-1845.

[13] Mirimani S M, Vahedi A, Marignetti F, et al. An online method for static eccentricity fault detection in axial flux machines[J]. IEEE Transactions on Industrial Electronics, 2015, 62(3)： 1931-1942.

[14] Zhu Z Q, Howe D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors, part 3： effect of stator slotting[J]. IEEE Transactions on Magnetics, 1993, 29(1)： 143-151.

[15] Zarko D, Ban D, Lipo T A. Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent-magnet motor using complex relative air-gap permeance[J]. IEEE Transactions on Magnetics, 2006, 42(7)： 1828-1837.

[16] Choi J Y, Lee S H, Ko K J, et al. Improved analytical model for electromagnetic analysis of axial flux machines with double-sided permanent magnet rotor and coreless stator windings[J]. IEEE Transactions on Magnetics, 2011, 47(10)： 2760-2763.

（编辑 于玲玲）

Modeling and Analysis of Unbalanced Moment for an Axial-Flux in-Wheel Motor with Eccentricity

Deng Wenzhe Zuo Shuguang Lin Fu Wu Shuanglong Mao Yu
（Clean Energy Automotive Engineering Centre Tongji University Shanghai 201804 China）

In order to analyze the impact of static and dynamic eccentricity, a quasi-3D analytical model of air-gap magnetic field was firstly built for an axial-flux in-wheel motor (AFWM) without eccentricity, and the slotting effect and fringing effect was taken into account through complex relative air-gap permeance and correction function respectively. Then the analytical model under eccentric condition was gained by means of considering the variation of air gap length, and finite element (FE) analysis results indicate that the model can predict air gap flux density precisely at arbitrary position of the AFWM with both static and dynamic eccentricity. Finally, the effects of eccentricity on magnetic field and electromagnetic force were analyzed via the established model and the method to calculate bending moment was proposed. The results reveal that apart from unbalanced magnetic pull, eccentricity in AFWM will produce extra bending moment, which is quite different from radial-flux motor. The bending moment may cause eccentric degree further deterioration.

Axial-flux in-wheel motor, static eccentricity, dynamic eccentricity, analytical model, bending moment

TM351

邓文哲 男，1993年生，博士研究生，研究方向为分布式驱动电机振动与噪声。

E-mail： deng_wenzhe@foxmail.com

左曙光 男，1968年生，教授，博士生导师，研究方向为汽车振动与噪声控制。

E-mail： sgzuo@tongji.edu.cn（通信作者）

10.19595/j.cnki.1000-6753.tces.160732

国家自然科学基金（51375343）和重大科研仪器设备专项（2012YQ150256）资助项目。

2016-05-22 改稿日期 2016-08-09