多模块并联逆变器系统中网侧电抗对谐振特性的影响分析

张 磊 王晓声 孙 凯 周洪伟

（1. 特变电工西安电气科技有限公司 西安 710119 2. 清华大学电机系 电力系统及发电设备控制和仿真国家重点实验室 北京 100084）

多模块并联逆变器系统中网侧电抗对谐振特性的影响分析

张 磊1王晓声2孙 凯2周洪伟1

（1. 特变电工西安电气科技有限公司 西安 710119 2. 清华大学电机系 电力系统及发电设备控制和仿真国家重点实验室 北京 100084）

新能源并网发电系统中常采用LCL型滤波器的多台逆变器模块化并联结构。由于LCL型滤波器本身故有的谐振特性，故实际应用中常采用无源阻尼或者有源阻尼的方法抑制谐振峰幅值。在理论研究中，通常将电网抽象为理想三相电压源而未考虑网侧电抗取值对系统谐振特性的影响；但在实际工程应用中，由于变压器漏感或线路自感等因素电网侧存在不可忽略的电抗。该文从多模块并联逆变器系统的控制结构入手，通过建立数学模型给出多台逆变器并联情况下系统谐振特性的分析方法，提出单台等效模型，并定义了新的变量——网侧总电抗Lc。深入分析使用有源阻尼时网侧总电抗取值对常用阻尼策略效果的影响，并给出保证系统稳定前提下网侧总电抗的取值范围。仿真和实验结果验证了理论分析的正确性。

并网逆变器 LCL型滤波器 并联运行 有源阻尼

0 引言

近年来，以风能、太阳能为代表的新能源在发电系统中所占的比重不断上升。为了将电能传输到更远的地方，往往需要将新能源发电系统并网运行，而PWM逆变器就承担起了接口变换器的角色，实现与外部电网之间可控的能量交换。此外，由于实际应用中单台逆变器的容量有限，为了提高新能源发电系统的输出功率，往往需要将多台逆变器并联运行。

为了抑制输出电流中由于开关动作引入的高频谐波，并网逆变器的输出端通常采用L型或者LCL型滤波器。与L型滤波器相比，LCL型滤波器在同样的滤波效果下有更小的体积和成本，动态性能良好，近些年来得到了广泛的关注和应用。然而，由于LCL型滤波器使用了三个独立的储能元件，使得其在谐振频率处存在幅值尖峰，对系统的稳定性造成影响[1-3]。

目前，解决谐振问题的主流方法有无源阻尼（Passive Damping, PD）和有源阻尼（Active Damping, AD）两大类。其中，有源阻尼方法不需要实际的电阻，而是通过改变控制结构来抑制系统的谐振峰。P. A. Dahono基于无源阻尼的思想首先提出了“虚拟电阻”的概念[4]。随后，出现了一大类基于变量反馈的有源阻尼方法[5-12]，其中典型的包括电容电流反馈、电容电压反馈、电感电流反馈等。文献[13]对这一类方法进行了总结，深入分析了上述方法能实现有源阻尼的机制。然而，目前大多数研究工作都简单地把电网抽象为理想电压源，而未对网侧漏电抗存在的条件下系统特性和有源阻尼策略进行研究。

实际应用中，往往需要将多台逆变器并联后接入电网，此时的系统谐振特性将发生变化，而针对单台逆变器设计的有源阻尼方法的效果也将受到影响[15-17]。此时有必要对多并联情况下的逆变系统进行数学建模，分析并联个数对系统特性的影响。图1给出了多模块并联逆变器系统的结构示意图。

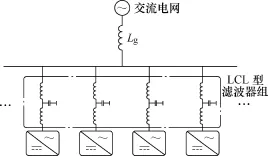
图1 多模块并联逆变器系统示意图Fig.1 Configuration of multi-module parallel inverter system

本文首先通过数学建模和分析建立多台逆变器并联时系统谐振特性和稳定性的研究方法。随后，针对几种常用的有源阻尼策略分析网侧漏电抗存在条件下的多模块并联逆变器系统谐振特性，并研究了漏电抗大小以及并联台数对于系统稳定性的影响。仿真和实验结果验证了理论分析的正确性。

1 多并联系统特性分析方法

1.1 单台逆变器控制结构分析

设Z1=L1s，Z2=L2s，Zc=1/(sC)，构成LCL型滤波器；Zg为电网侧的等效漏电抗，Zg=Lgs；uinv为逆变器输出电压，ug为电网电压。一般来说，并网逆变器的控制对象既可以是逆变器侧电流i1也可以是网侧电流i2，本文考虑控制i1的情况。可以推导得出输出电压、电网电压到输出电流的传递函数表达式分别为

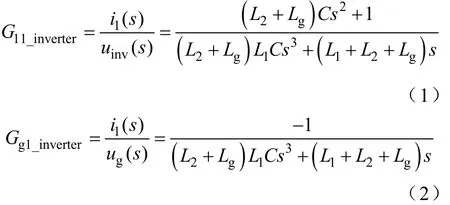
谐振峰的频率和幅值的计算相关文献中均已给出，这里不再赘述。由式（1）和式（2）可知，网侧漏电抗Lg会直接影响逆变器的谐振特性。以使用电容电流反馈为例，图2给出了此时的单台逆变器的控制结构图。图中iref为参考电流，这里为工频正弦量，相位由锁相环产生，幅值由上层功率控制器给出。Gpr(s)为比例谐振控制器的传递函数，Gd(s)代表由于PWM开关动作引入的等效延迟环节，其表达式可以写为

式中，T为开关周期。

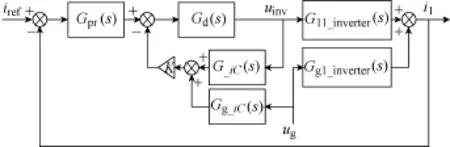
图2 含电容电流反馈的并网逆变器控制结构Fig.2 Control configuration of grid-connected inverter with capacitor current feedback

此外，图2中G_iC(s)代表输出电压到电容电流的传递函数，Gg_iC(s)代表电网电压到电容电流的传递函数，表达式为

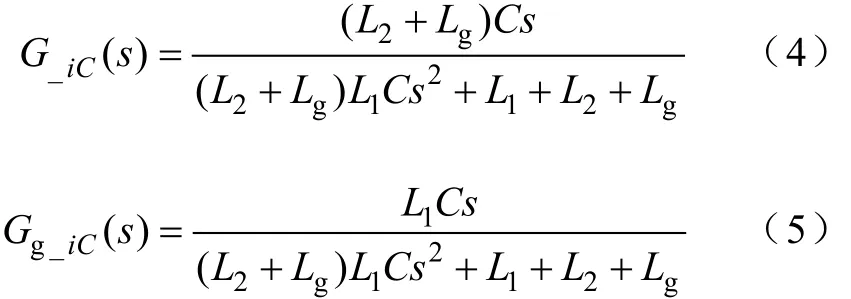
电容电流经过比例环节反馈到控制器的输出端[7,11-13]，实现阻尼效果。

1.2 多并联系统控制结构分析

实际应用中，单台并网的情况并不多见，常用的是多台逆变器并联后统一接入大电网。根据文献[15,16]，多台LCL型滤波逆变器并联后系统谐振特性将发生变化。图3给出了并联系统的阻抗网络示意图。

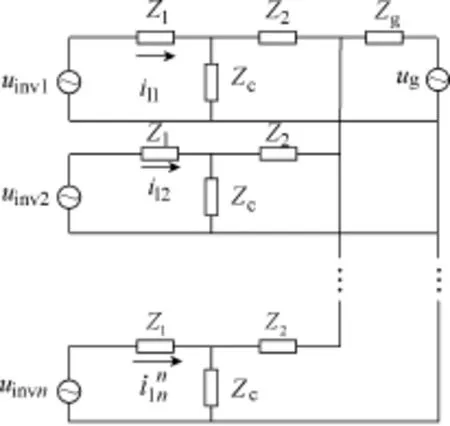
图3 并联系统阻抗网络示意图Fig.3 Impedance network of multi-parallel system

图3中各逆变器输出电流与各逆变器输出电压以及电网电压的关系为

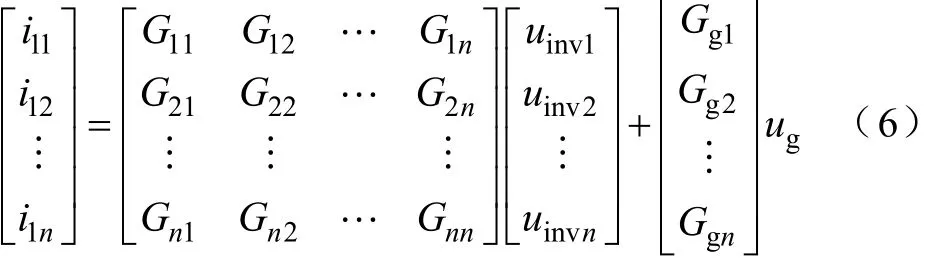
式中，由于系统结构的对称性和参数的一致性，有G11=G22=…=Gnn，Gij（i≠j）取值相等，Gg1=Gg2=…= Ggn。基于上述分析，可以得到多台逆变器并联时完整系统的控制结构如图4所示[17]。此时，图4表示的是一个典型的多输入多输出系统。图中的Gpr(s)为PR控制器传递函数矩阵，Gd(s)为等效延迟环节传递函数矩阵；由于各台逆变器独立控制，故它们均为对角矩阵。G(s)与Gg(s)与式（6）中的矩阵对应。此时电流参考值为矩阵形式Iref(s)，输出电流也为矩阵形式I1(s)，则从电流参考值Iref(s)和电网电压Ig(s)到输出电流I1(s)的闭环传递函数为矩阵形式，即

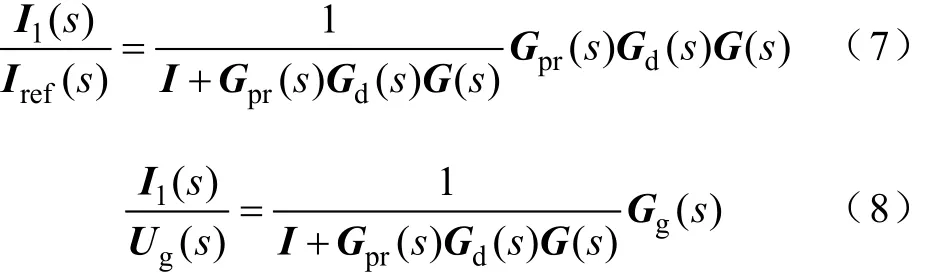
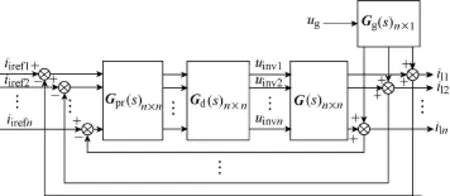
图4 并联系统控制结构图Fig.4 Control structure of multi-parallel system

对于式（6），如果各台逆变器完全相同，则有i11=i12=…=i1n、uinv1=uinv2=…=uinvn。此时对于任意一台逆变器有

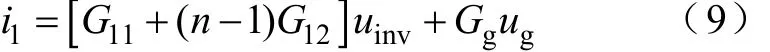
如果设Geq=G11+(n-1)G12，则有

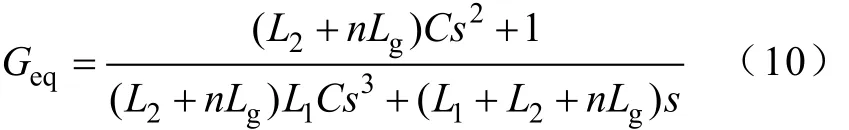
此外，推导可得

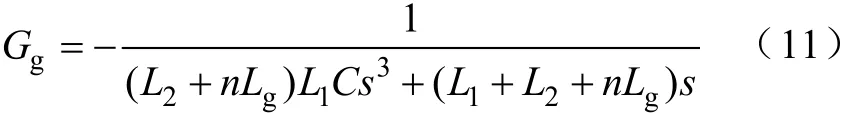
容易发现，将式（1）中的Lg用nLg代替即可得到式（10），将式（2）中的Lg用nLg代替即可得到式（11）。可见，n台逆变器并联时逆变器的输出端“看到”的网侧阻抗与单台时相比相当于放大了n倍，可以将n台并联逆变系统等效为n个独立的单输入单输出系统，从而大大简化了系统特性的分析。于是，对于n台逆变器并联的情况，只需要将图2中的G11_inverter与Gg1_inverter分别替换为Geq与Gg即可得到n台逆变器并联时一台逆变器的等效模型。

下面考虑使用有源阻尼策略后的系统特性，这里以电容电流反馈为例。此时系统的控制结构图较复杂，这里不再给出，但可以类似地推导出传递函数的矩阵形式为

其中

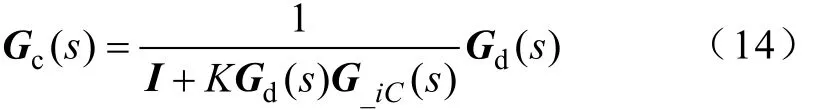
式（12）～式（14）中，G_iC(s)为n×n方阵，Ggeq_iC(s)为n×1矩阵。类似地，可以构建单台等效控制结构图。首先，需要将图2中的G11_inverter与Gg1_inverter分别替换为Geq与Gg。由方阵G_iC(s)，可以得到

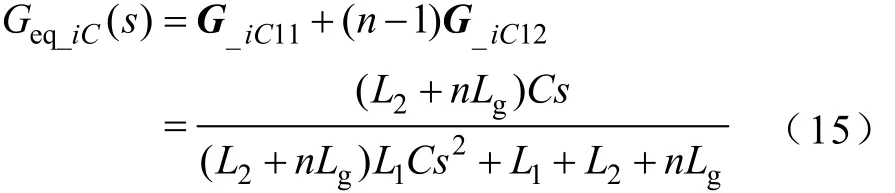
此外，推导可得

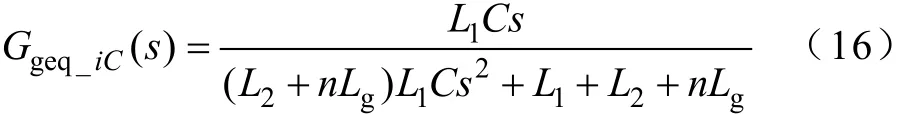
容易发现，将（4）和式（5）中的Lg用nLg代替即可得到式（15）和式（16）。于是，用Geq_iC与Ggeq_iC分别代替图2中的G_iC与Gg_iC即可得到使用电容电流反馈时的适用于多并联系统分析的单台等效模型。类似地，对电容电压反馈与虚拟电阻也可以用类似的方法得到相应的单台逆变器等效模型，其结果都相当于将单台逆变器模型中的网侧漏抗Lg放大为原来的n倍。

为了方便后面的分析，这里将nLg定义为新的变量——网侧总电抗Lc。

2 有源阻尼方法下多模块并联逆变器系统谐振特性分析

本节将针对多模块并联逆变器系统，分析网侧总电抗Lc对逆变系统特性的影响。首先不使用有源阻尼策略，从图2可以推导出Lc变化时电流给定iref和电网电压ug到输出电流i1的闭环伯德图（分别为图5上、下）。

图5中使用的主要参数见表1。其中网侧电感L2的取值为0，这是为了与实际项目对应；当L2不为0时结论类似。

图5 控制系统闭环传递函数伯德图Fig.5 Bode plot of closed-loop transfer function of control system

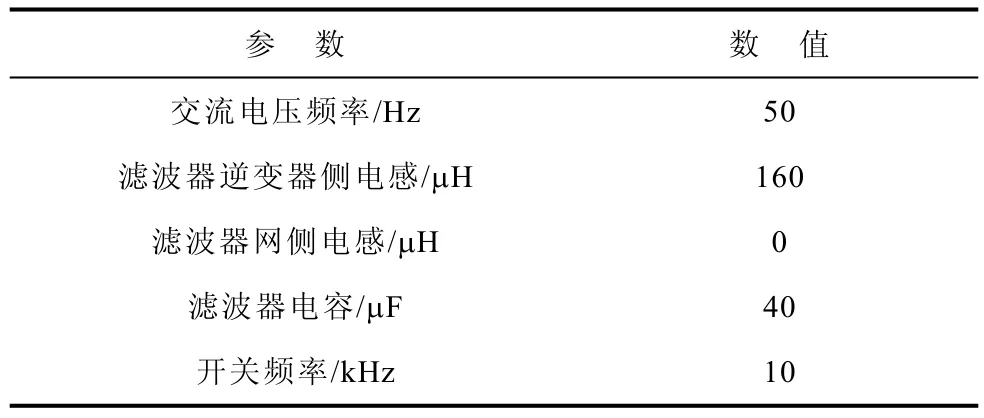
表1 并网逆变器系统参数Tab.1 Parameters of the grid-connected inverter

由图5可见，随着Lc的增大，闭环伯德图的谐振频率逐渐减小，谐振峰幅值略有减小。对于电流给定到输出电流的伯德图，Lc的变化仅对谐振频率附近频段产生影响，而对低频段和更高频段没有影响。此外，可以注意到在4krad/s附近有一个次谐振峰，该谐振峰不受Lc取值的影响，是控制器引入的。然而，该谐振峰可能对系统稳定性造成影响，后面会有分析。对于电网电压到输出电流的伯德图，Lc的取值只会影响谐振频率及以上频段的波形而对低于谐振频率的频段没有影响。图5下图在工频处形成了一个反谐振峰，这是因为PR控制器的谐振频率设定为工频，从而有效地抑制了电网电压对输出电流的影响。众所周知，电网背景谐波中有一类是工频整数倍的低频谐波（5次、7次等）。在并网逆变器应用中，为了抑制低频电网谐波对并网电流的影响，一种常见的方法是同时使用多个谐波频率处的PR控制器，从而抑制电网谐波对特定频次电流的增益。对电网低频谐波的抑制不是本文考虑的内容，本文主要关注对高频谐波的抑制效果。

下面将对几种典型的有源阻尼策略进行分析，研究网侧总电抗取值对阻尼效果的影响以及阻尼策略对电网谐波的抑制效果。

2.1 电容电流反馈

对于电容电流反馈，放大系数K是可以调节的变量，只有K取值恰当时才能在保证系统稳定的前提下抑制谐振。图6给出了反馈系数K在0～100范围内变化时系统的根轨迹，系统参数与表1相同。从图中可以看出，闭环系统共有5个根，图中标出了K=0时的闭环极点坐标，箭头方向表示特征根随K值增大而移动。

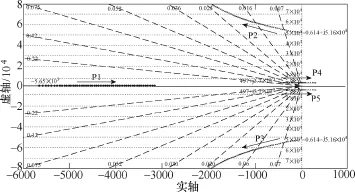
图6 电容电流反馈控制系统根轨迹Fig.6 Root locus of control system with capacitor current feedback

图6中引起振荡的是P2、P3和P4、P5两对极点。随着K值的增大，P1频率逐渐减小但阻尼为1，不存在超调。P2、P3为主谐振极点，随着K的增大谐振频率增大，阻尼增大，超调量减小。P4、P5为次谐振极点，随着K的增大，谐振频率逐渐减小，阻尼减小，超调增大；在图中的参数取值下，当K＞42时P4、P5进入右半平面，系统失稳。

下面考虑网侧总电抗Lc取值对系统稳定性的影响，图7给出了Lc变化时系统的根轨迹（反馈系数K=10），其中箭头方向代表Lc从0不断增大。在所给参数下，当Lc＞50μH时，次谐振极点（P4、P5）进入右半平面，系统失稳。在系统稳定的前提下，随着Lc的增大，主谐振极点P2、P3频率减小，阻尼增大，谐振峰幅值减小。可见，在系统稳定的前提下，较大的Lc取值反而会对谐振有抑制效果。图8上、下分别给出了Lc变化时电流给定iref和电网电压ug到输出电流i1的伯德图。

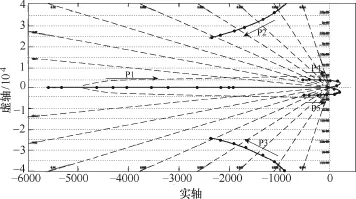
图7 Lc取值变化时控制系统根轨迹Fig.7 Root locus of control system with different value of Lc

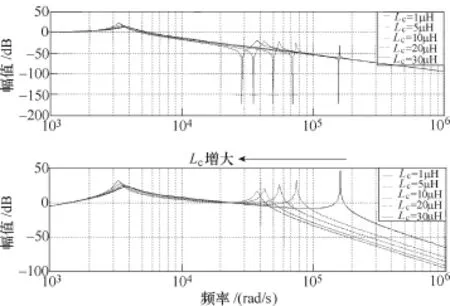
图8 Lc取值变化时控制系统伯德图Fig.8 Bode plot of control system with different value of Lc

可见，当Lc变化时，电容电流反馈策略对逆变器输出电压侧引入的高频谐波抑制效果很好；而对电网电压引入的高频谐波抑制效果较差且受Lc取值影响。Lc取值增大时，谐振峰的幅值反而越小；而且即使Lc取值很大，谐振峰的幅值也在0dB以上。

2.2 电容电压反馈

文献[13]指出，对于电容电压，为了获得良好的阻尼效果，需要对滤波电容电压进行微分反馈。然而由于实际系统中微分反馈难以实现，故比较实用的方法有数字离散化和高通滤波[10,11]。由于本文基于连续域进行分析，故这里采用高通滤波器。从逆变器输出电压uinv和电网电压ug到电容电压的传递函数为

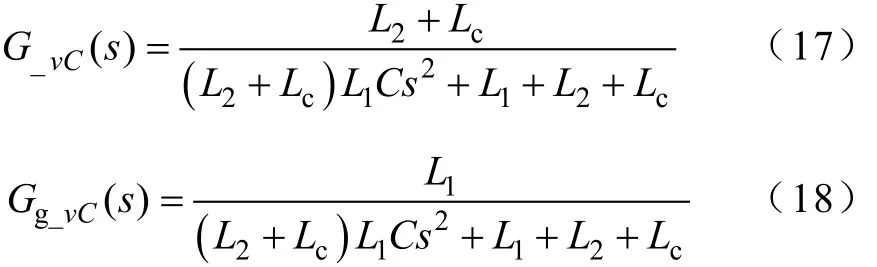
与电容电流反馈中的分析类似，改变反馈系数K的取值可以观察K值对系统稳定性以及谐振阻尼性能的影响。与电容电流反馈相比，由于增加了HPF环节，故引入了一个新的极点。从根轨迹中（图略）可以得知，只有当K＜32时系统才稳定。在稳定的范围内，随着K增大，主谐振极点的频率基本不变，阻尼逐渐增大；次谐振极点的频率变化不大，阻尼逐渐增大。通过伯德图可以看出，电容电压反馈对逆变器输出电压引入的高频谐波抑制效果良好；对电网电压的高频谐波也有一定的抑制效果，但作用有限。

类似地，可以分析网侧总电抗Lc取值对系统稳定性的影响。图9给出了Lc变化时使用电容电压反馈控制的系统根轨迹（反馈系数K=5），图中箭头方向代表Lc增大的方向。

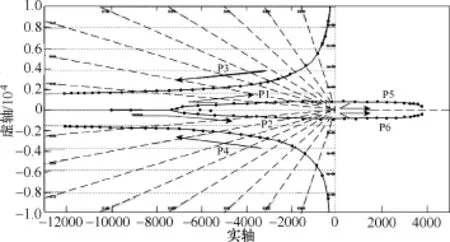
图9 Lc取值变化时控制系统根轨迹Fig.9 Root locus of control system with different value of Lc

可见，由于在反馈通道上使用了高通滤波器，故系统极点由原来的5个变为6个。随着Lc的增大，主谐振极点P3、P4频率减小，阻尼增大；次谐振极点P5、P6频率增大，阻尼先减小后增大。当Lc＞90μH时，P1、P2进入右半平面，系统失稳。类似地，可以得到Lc变化时系统伯德图，其特性与图8给出的结果类似。

2.3 虚拟电阻

虚拟电阻的概念最早在文献[4]中被提出，后来得到诸多学者的深入研究和应用。文献[14]对使用虚拟电阻时滤波器参数对系统稳定性和阻尼效果的影响进行了分析，文献[16]针对多并联系统引入虚拟电阻的方法，有效抑制了多种谐振现象。

本文采用在滤波电容上并联虚拟电阻的方式抑制谐振。图10给出了Lc变化时系统的根轨迹，箭头方向为Lc增大方向（虚拟电阻Rv=1Ω）。由图可见，随着Lc增大，主谐振极点P2、P3频率减小，阻尼增大；次谐振极点P4、P5频率减小，阻尼减小。当Lc＞68μH时，系统失稳。使用虚拟电阻时系统对谐波的抑制效果和特点与电容电流反馈和电容电压反馈类似。

3 仿真与实验

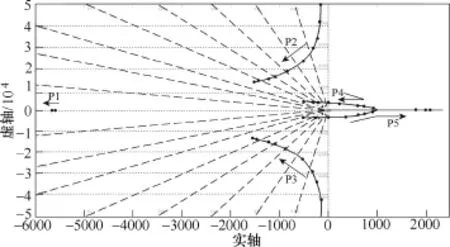
图10 Lc取值变化时控制系统根轨迹Fig.10 Root locus of control system with different value of Lc

为了验证上述分析结果，以电容电流反馈方法为例进行仿真研究（反馈系数K=10），主要参数见表1。仿真中，设置输出电流参考值为iref=30A。图11给出了网侧总电抗Lc取值不同时的输出电流响应。根据2.1节中的分析，当Lc＞50μH时次谐振极点进入右半平面导致系统失稳。从图11可看出，当Lc=10μH时输出电流经过短暂动态过程后准确跟随参考值。当Lc=60μH时输出电流发散，远远超出变换器的实际工作范围。为了更好地观察输出电流波形，可以观察0～0.03s的输出电流波形，可以看出输出电流以一固定频率振荡，且幅值不断增大。测量可知，其振荡频率即为次谐振极点对应的频率。

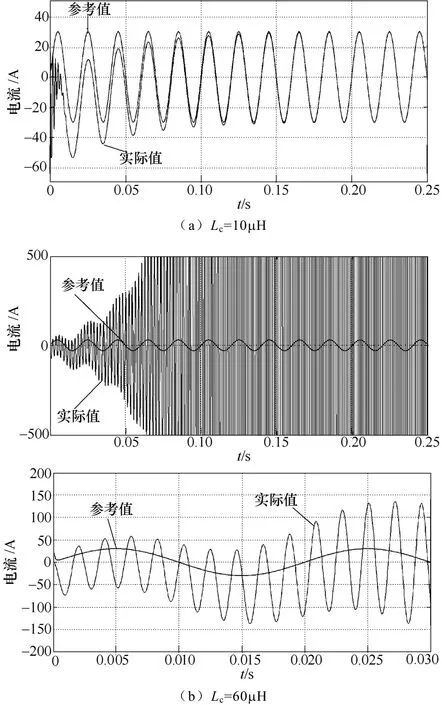
图11 网侧总电抗不同时输出电流仿真结果Fig.11 Simulation results of output current with different value of Lc

此外，可以在电网电压中注入特定频次的谐波，观察其对输出电流的影响。根据图8，当Lc取值不同时，相同的网侧电压谐波将对输出电流产生不同的影响。例如，在电网电压中注入幅值为0.3%基波的谐波，其频率为图8中Lc=10μH时对应的谐振频率，图12给出了输出电流波形和傅里叶分析结果。当Lc= 10μH时输出电流THD为4.95%，而当Lc=1μH时输出电流THD为1.07%，这与图8给出的结论相符。

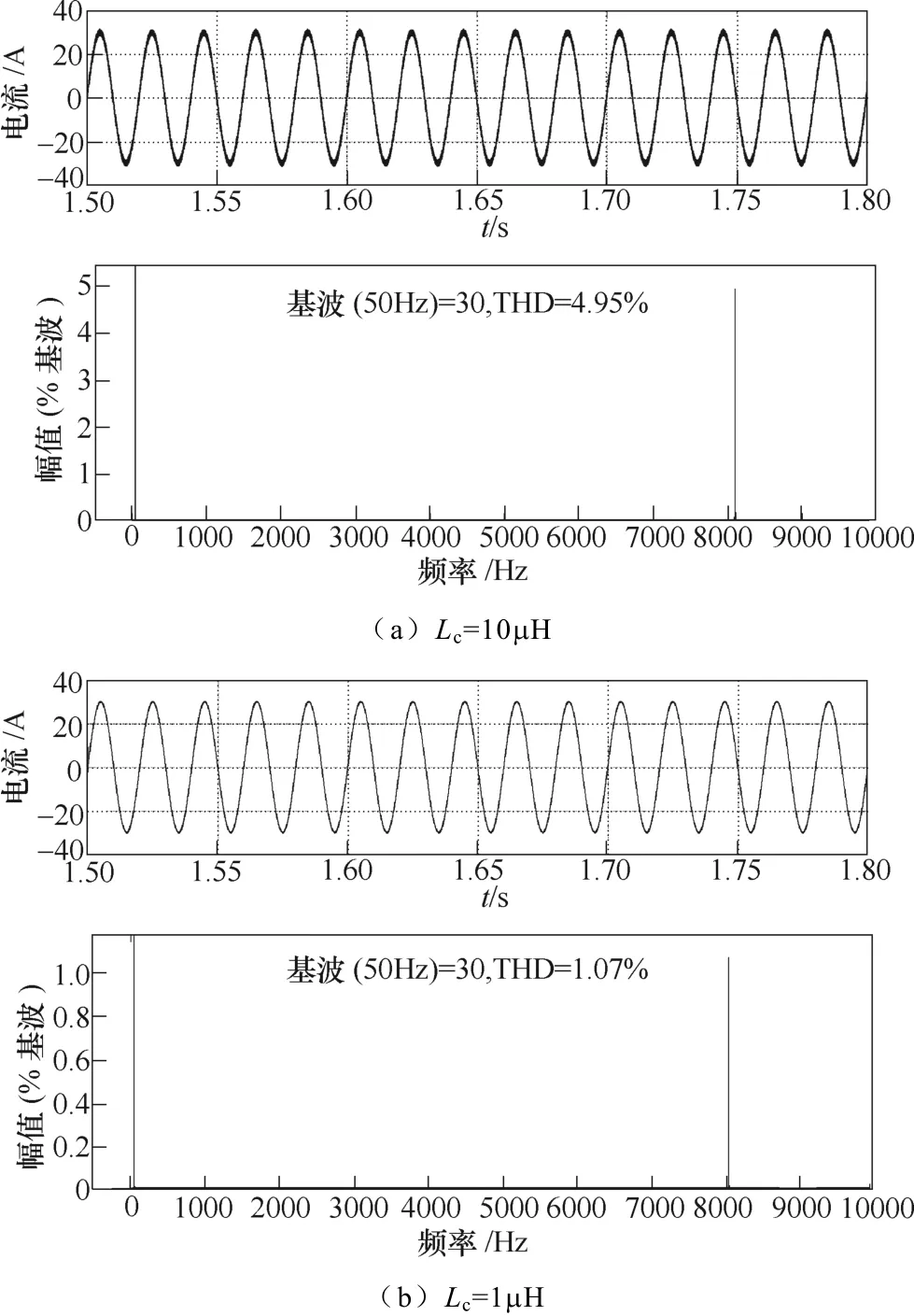
图12 网侧谐波对输出电流影响仿真结果Fig.12 Simulation results of output current with grid-side harmonics

为了验证第2节给出的结论，对Lg=10μH、n=1和Lg=1μH、n=10两种情况进行仿真，电网电压中注入与上述仿真中相同的谐波。对两种情况下逆变器的输出电流进行傅里叶分析，可得图13所示的结果。从中可以看出，网侧谐波对两种情况下逆变器输出电流的影响完全相同，输出电流THD均为4.95%。

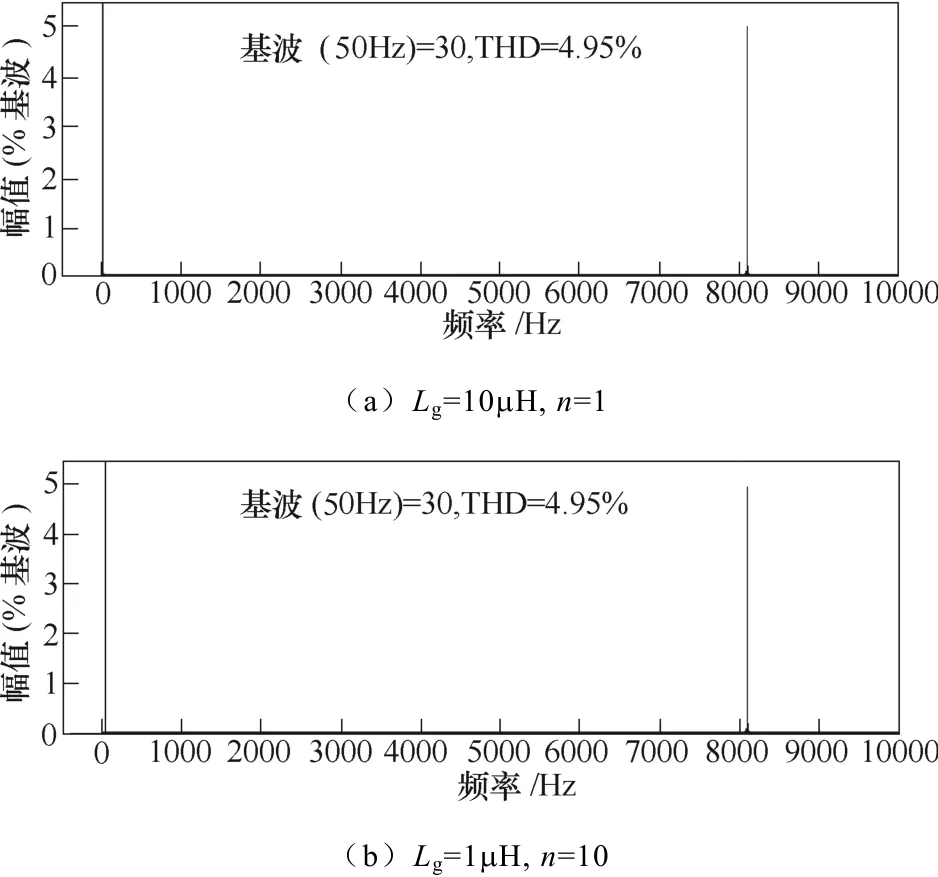
图13 两种情况下输出电流傅里叶分析结果Fig.13 Fourier analysis results of output current with different conditions

此外，还可以通过实验对上述结论进行验证。图14给出了Lg=30μH、n=1，Lg=15μH、n=2和Lg=10μH、n=3三种工况下的电网电压、输出电流波形，主要实验参数见表1，逆变器单台功率为165kW。实验中，电网电压含有相同的谐波成分。图14中还给出了n=2、n=3两种情况下逆变器之间的环流。

从图14可以看出，三种工况下逆变器输出电流中的谐波成分相同；即当nLg为定值时，输出电流有相同的谐波特性。

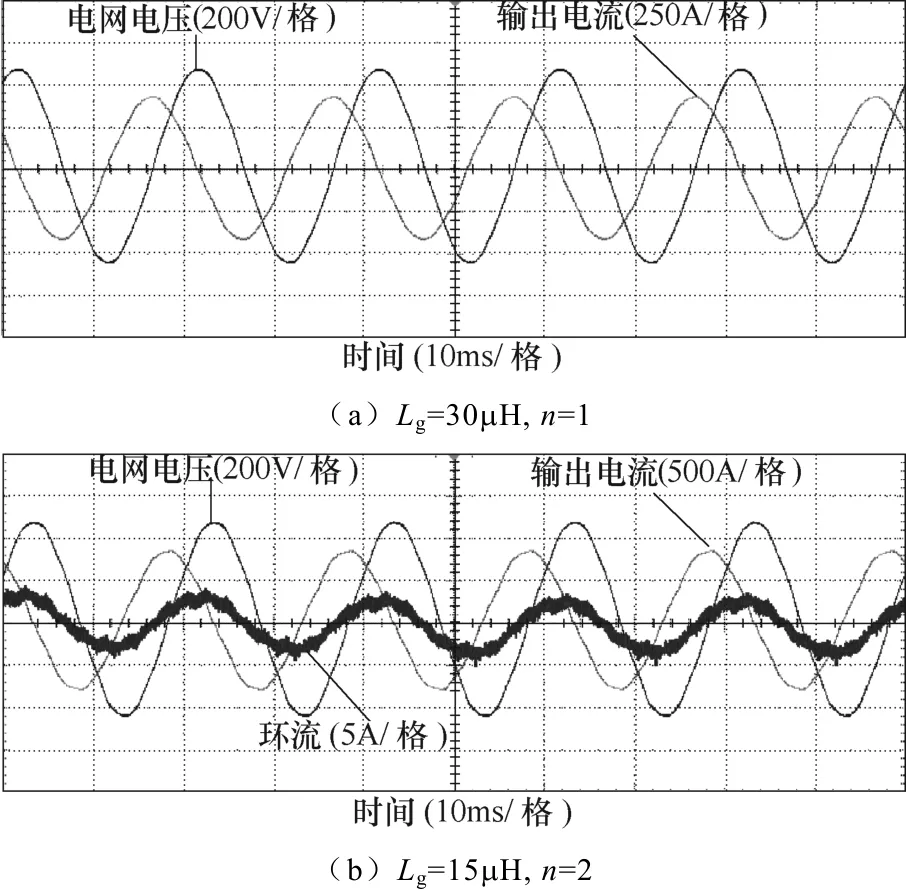
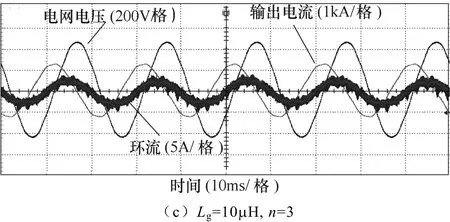
图14 不同工况下逆变器输出电流波形Fig.14 Waveforms of inverter output current with different conditons

4 结论

本文针对多模块并联逆变器系统，对其谐振特性进行了深入分析，并重点研究了在使用了有源阻尼策略前提下网侧总电抗Lc对系统谐振特性和稳定性的影响。此外，本文还分析了常用有源阻尼策略对电网电压中谐波的抑制效果。得出以下结论：

1）对于多模块并联逆变器系统，可以采用单台等效模型分析其稳定性和谐振特性。如果设逆变器台数为n，则nLg决定逆变器的特性。

2）网侧总电抗Lc的大小同时影响系统谐振峰的频率和幅值。

3）常用有源阻尼策略对于逆变器输出侧引入的高频谐波有良好的抑制效果；而对电网电压中引入的高频谐波抑制效果有限。

4）网侧总电抗Lc的取值影响系统的稳定性。对于特定的阻尼策略，当Lc取值过大时，系统的一对特征根将进入右半s平面，导致系统失稳；在稳定的前提下，Lc取值较大反而可以抑制网侧电压谐波对输出电流的影响。

[1] 黄挚雄, 徐保友, 沈玲菲, 等. LCL并网逆变器新型电流双闭环控制策略研究[J]. 电力系统保护与控制, 2012, 40(17)： 1-5. Huang Zhixiong, Xu Baoyou, Shen Lingfei, et al. New current double closed loop control strategy of LCL grid-connected inverter[J]. Power System Protection and Control, 2012, 40(17)： 1-5.

[2] 白志红, 阮新波, 徐林. 基于LCL滤波器的并网逆变器的控制策略[J]. 电工技术学报, 2011, 26(1)：118-124. Bai Zhihong, Ruan Xinbo, Xu Lin. Control strategies for the grid-connected inverter with LCL filter[J]. Transactions of China Electrotechnical Society, 2011, 26(1)： 118-124.

[3] 雷亚雄, 李建文, 李永刚. 基于准PR调节器电流双闭环LCL三相并网逆变器控制[J]. 电力系统保护与控制, 2014, 42(12)： 44-50. Lei Yaxiong, Li Jianwen, Li Yonggang. Control strategy of three-phase LCL grid-connected inverter based on quasi-PR adjuster[J]. Power System Protection and Control, 2014, 42(12)： 44-50.

[4] Dahono P A. A control method to damp oscillation in the input LC filter of AC-DC PWM converters[C]// IEEE Power Electronics Specialists Conference, Cairns, Qld., 2002： 1630-1635.

[5] 陈新, 韦徵, 胡雪峰, 等. 三相并网逆变器LCL滤波器的研究及新型有源阻尼控制[J]. 电工技术学报, 2014, 29(6)： 71-79. Chen Xin, Wei Zheng, Hu Xuefeng, et al. Research on LCL filter in three-phase grid-connected inverter and novel active damping control strategy[J]. Transactions of China Electrotechnical Society, 2014, 29(6)：71-79.

[6] 贾鹏宇, 李艳, 郑琼林. 电压型级联系统中减小源变换器输出阻抗的有源阻尼控制方法[J]. 电工技术学报, 2014, 30(8)： 71-82. Jia Pengyu, Li Yan, Zheng Qionglin. An active damping method to reduce output impedance of converters in voltage source cascaded system[J]. Transactions of China Electrotechnical Society, 2014, 30(8)： 71-82.

[7] 庄强, 叶永强, 赵强松, 等. 基于分裂电容法的LCL并网逆变器控制策略分析与改进[J]. 电工技术学报, 2015, 30(16)： 85-93. Zhuang Qiang, Ye Yongqiang, Zhao Qiangsong, et al. Analysis and improvement of the control strategy of LCL grid-connected inverter based on splitcapacitor[J]. Transactions of China Electrotechnical Society, 2015, 30(16)： 85-93.

[8] 韩刚, 蔡旭. LCL并网变流器反馈阻尼控制方法的研究[J]. 电工技术学报, 2014, 42(17)： 72-78. Han Gang, Cai Xu. Study on feedback damping control methods of grid-connected inverter with LCL filter[J]. Transactions of China Electrotechnical Society, 2014, 42(17)： 72-78.

[9] 周乐明, 罗安, 陈燕东, 等. 单相LCL型并网逆变器功率控制及有源阻尼优化方法[J]. 电工技术学报, 2016, 31(6)： 144-154. Zhou Leming, Luo An, Chen Yandong, et al. A singal-phase grid-connected power control and active damping optimization strategy with LCL filter[J]. Transactions of China Electrotechnical Society, 2016, 31(6)： 144-154.

[10] Mariusz Malinowski, Steffen Bernet. A simple voltage sensorless active damping scheme for threephase PWM converters with an LCL filter[J]. IEEE Transactions on Industrial Electronics, 2008, 55(4)：1876-1880.

[11] Dannehl J, Fuchs F, Hansen S, et al. Investigation of active damping approaches for PI-based current control of grid-connected PWM converters with LCL filters[C]//IEEE Energy Conversion Congress and Exposition, San Jose, CA, 2009： 2998-3005.

[12] 张宪平, 李亚西, 许洪华. 新型拓扑滤波器的双馈风电网侧变流器阻尼策略[J]. 中国电机工程学报, 2009, 29(21)： 1-7. Zhang Xianping, Li Yaxi, Xu Honghua. Damping strategy of grid-side converter with new topology filter in doubly-fed wind power system[J]. Proceedings of the CSEE, 2009, 29(21)： 1-7.

[13] 许津铭, 谢少军, 肖华锋. LCL滤波器有源阻尼控制机制研究[J]. 中国电机工程学报, 2012, 32(9)：27-33. Xu Jinming, Xie Shaojun, Xiao Huafeng. Research on control mechanism of active damping for LCL filters[J]. Proceedings of the CSEE, 2012, 32(9)： 27-33.

[14] Wessels C, Dannehl J, Fuchs F. Active damping of LCL-filter resonance based on virtual resistor for PWM rectifiers-stability analysis with different filter parameters[C]//IEEE Annual Power Electronics Specialists Conference, Rhodes, 2008： 3532-3538.

[15] 陆晓楠, 孙凯, 黄立培. 微电网系统中基于双二阶滤波器的主动阻尼方法[J]. 电工技术学报, 2013, 28(3)： 261-268. Lu Xiaonan, Sun Kai, Huang Lipei. Active damping method based on bi-quad filter for microgrid applications[J]. Proceedings of the CSEE, 2013, 28(3)：261-268.

[16] He Jinwei, Li YunWei, Dubravko B, et al. Investigation and active damping of multiple resonances in a parallel-inverter-based microgrid[J]. IEEE Transactions on Power Electronics, 2013, 28(1)： 234-246.

[17] Juan L A, Mikel B, Jesus L, et al. Modeling and control of N-paralleled grid-connected inverters with LCL filter coupled due to grid impedance in PV plants[J]. IEEE Transactions on Power Electronics, 2011, 26(3)： 770-785.

（编辑 郭丽军）

Analysis of Grid-Side Reactance’s Impact on Resonance Characteristic of Multi-Module Parallel Inverter System

Zhang Lei1Wang Xiaosheng2Sun Kai2Zhou Hongwei1
（1. TEBA Xi’an Electric Technology Co. Ltd Xi’an 710119 China 2. State Key Lab of Control and Simulation of Power Systems and Generation Equipments Department of Electrical Engineering Tsinghua University Beijing 100084 China）

The interfacing inverters are usually parallel-connected with modules via LCL filters in a grid-connected new energy generation system. Because of resonance problems of LCL filters, passive and active damping is commonly used to damp the resonance in application. In theoretical analysis, the grid is usually treated as an ideal three-phase voltage source without considering the impacts of grid-side reactance on resonance characteristic. But in industrial applications, however, there is a non-negligible reactance on the grid side because of transformers and wires. Based on the control structure and mathematical modeling, the analysis method of multi-module parallel system is given. Equivalent single model is proposed, and a new variable is defined as grid-side total reactance Lc. Damping effects of several common AD methods with different values of Lcare studied. Moreover, the allowable value range of Lcis given considering system stability. Simulation and experimental results have testified the correctness of theoretical analysis.

Grid-connected inverter, LCL filter, parallel operation, active damping

TM46

张 磊 男，1979年生，博士，高级工程师，研究方向为电力电子与新能源发电。

E-mail： 18729278329@139.com

孙 凯 男，1977年生，博士，副教授，研究方向为电力电子与新能源发电。

E-mail： sun-kai@mail.tsinghua.edu.cn（通信作者）

10.19595/j.cnki.1000-6753.tces.161103

国家高技术研究发展计划（863计划）（2015AA050606）和国家自然科学基金（51677054、51177083）资助项目。

2016-07-14 改稿日期 2016-08-06