复杂有源配电网供电路径快速优化

迟吉运 韦 钢 李功新 李沁愉 张嘉堃

（1. 上海电力学院 上海 200090 2. 福建省电力公司 福州 350000 3. 上海市供电公司 上海 200233）

复杂有源配电网供电路径快速优化

迟吉运1韦 钢1李功新2李沁愉3张嘉堃1

（1. 上海电力学院 上海 200090 2. 福建省电力公司 福州 350000 3. 上海市供电公司 上海 200233）

配电网络结构日益复杂化以及分布式电源广泛接入带来的不确定性，增加了配电网供电路径优化的难度，传统配电网重构方法很难满足其快速性要求。针对风机、光伏出力的波动性，在构造的概率场景模型基础上，基于时间尺度进行出力分割，并利用无重复生成树策略对复杂搜索空间进行简化，避免重复性辐射型校验，减少解空间的冗余度，采取改进的编码策略以及改进的教学优化算法对重构模型进行求解，提高搜索的速度和全局寻优能力。算例分析证明了所提方法的快速性和有效性。

分布式电源 复杂性 网络重构 无重复生成树策略 改进教学优化算法 快速性

0 引言

配电网是连接输电网与电力用户的中间桥梁，其可靠、经济运行对整个电力系统的稳定性具有重要影响[1]。其中，有源配电网的相关研究是当前国内外热点，针对复杂有源配电网供电路径的优化问题，可以通过网络重构来实现，该方法操作简便且高效，具有明显的经济效益和社会效益[2,3]。

目前，分布式电源（Distributed Generation, DG）在配电网的接入比重逐渐增大，成为有源配电网的主要特征之一。其广泛接入在应对供电紧张等方面起到了重要作用，然而规模化接入的间歇性新能源出力具有不确定性，为有源配电网的协调控制带来极大挑战[4,5]。在传统的配电网研究中，为简化计算，分布式电源常常处理成“负”的恒功率模型[6-8]。该处理方法往往忽略其出力随机性对配电网供电路径优化产生的不确定影响，有失一般性。因此，传统的重构方法如启发式算法、人工智能算法及新兴的混合算法等[9-12]并不完全适用。场景分析[13-15]是解决随机问题的有效方法，目前已越来越多地应用到考虑DG不确定性出力影响的有源配电网研究中。然而，网络结构复杂性以及DG渗透率日益增加，会导致重构优化过程中产生组合爆炸问题，影响搜索效率，不满足复杂有源配电网供电路径快速寻优的要求。如何构造计算速度快，又能获得全局最优、适用于复杂有源配电网的重构方法具有一定的研究价值。

本文基于时间尺度来分割风机和光伏的出力波动，构造不同概率场景模型，利用无重复生成树策略以缩减复杂配电网供电路径搜索空间，减少无效解的产生，并结合十进制编码策略和改进教学优化算法的应用，提高重构方法全局寻优的搜索效率，算例分析证明了所提多方面优化的重构方法的快速性及有效性。

1 含DG概率场景的配电网重构模型

1.1 风机概率模型

针对风机输出功率与风速有关，具有不确定性，本文采用应用较为广泛的两参数Weibull分布函数F(v)来描述风速的概率分布，即

式中，k为形状参数，反映风速v的分布情况；c为尺度参数，表明该风场在某时刻的平均风速大小。

风机出力wP一般采用线性分段函数来描述，即

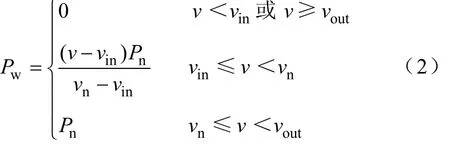
式中，vn、vin、vout分别为额定风速、切入风速和切出风速；Pn为风机的额定容量。

当vin≤v＜vn时，风电输出有功概率密度函数为

1.2 光伏概率模型

光伏发电输出功率与光照强度、光伏阵列有效面积和光电转换效率密切相关，光伏阵列的输出功率为

式中，E为实际光照强度；A为阵列总面积；η为光电转化效率。

在某个时段内（如1h），光照强度E可近似看成Beta分布，其概率密度函数为

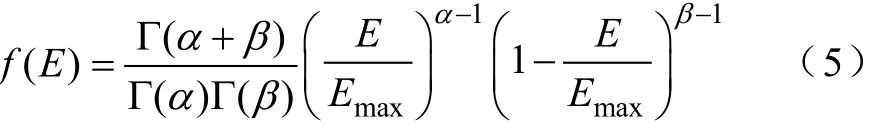
式中，maxE为光照强度最大值；α、β为分布的形状参数；Γ为伽马函数。

由式（4）、式（5）可得光伏阵列的概率密度函数为

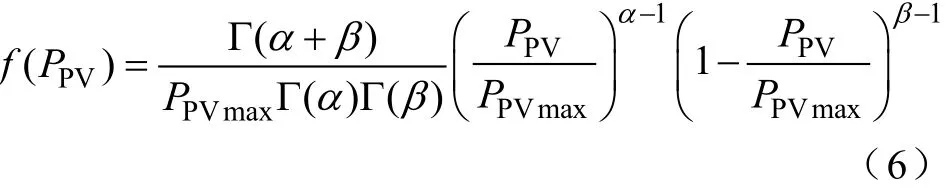
式中，PPVmax为光伏阵列最大输出功率，PPVmax= EmaxAη。

1.3 负荷概率模型

本文采用正态分布来描述负荷的不确定性，其合理性相关文献已验证，负荷的有功、无功功率概率密度函数为

式中，rP、rQ分别为节点r处的负荷有功和无功功率；rPμ、rQμ分别为节点r处的负荷有功和无功功率的均值；rPσ、rQσ分别为节点r处的负荷有功和无功功率的标准差。

1.4 供电路径重构模型

1.4.1 目标函数

供电路径重构一般以有功网损最小为目标，由于风机、光伏出力的不确定性，网损可采用其期望值来近似实际情况。因此，本文以有功网损期望值最小化作为目标函数，即

式中，E为系统有功网损总期望值，由其确定不同场景下整体最优；jp为场景j时的概率；jL为场景j时有功网损期望值；m为场景数；ir为支路i的电阻；l为支路总数；ijP、ijQ、ijU分别为支路i在场景j的有功功率、无功功率和电压。

1.4.2 约束条件

需要满足的约束条件主要为系统功率平衡约束、电压约束、DG出力功率上下限约束、支路容量约束等，即

式中，PDGi、QDGi分别为接在节点i的分布式电源所发出的有功和无功功率；PLi、QLi为接在节点i的负荷有功和无功需求；Gij为支路ij电导；Bij为支路ij电纳；θij为节点i与节点j的电压相位差；m为与节点i相联的支路数；miniU和maxiU分别为节点i的电压下限和上限，maxijS为支路ij允许通过的最大容量。

1.5 时序概率场景划分

在实际配电网中，影响风机、光伏出力特性的主要因素为风速和光照强度，不同类型的负荷需求变化主要受人为因素影响。由此可见，分布式电源的出力及不同负荷大小不是恒定不变的，而是随时间变化发生波动，具有明显的时序特性。并且，风机、光伏出力最大值以及负荷需求的高峰期时间段往往也不相同。以某地区的某一天为例，居民负荷的需求峰值主要集中在17∶00～21∶00，而光伏的出力最大值主要集中在12∶00～13∶00，存在一定的随机性。本文基于典型的风机、光伏以及不同负荷的时序曲线，采用时序场景分析法。根据风机、光伏以及负荷某天的接入情况，进行合理地出力分割，划分出不同时间段的场景模型，使其能够直观反映该时段内不同时序曲线的特征。例如，在某时间段内，普通负荷用电较少，而风机、光伏的出力在峰值附近波动[16]。通过时序场景划分，可以有效地将配电网中难以用数学模型描述的不确定性因素转化为较易求解的多个确定性场景问题来处理。不仅满足配电网运行的实际状况，而且避免建立复杂的随机性数学模型，降低建模和求解的难度，提高求解效率。本文为了更加简单明了地进行出力分割，将不同负荷的需求大小以及风机、光伏的出力值定义为高、中、低三个区间，不同的时序曲线设置区间大小不相同，但是前提必须要满足不同的时序曲线随时间变化特征。以某天的居民时序负荷曲线为例，负荷需求低于30%的负荷峰值时设为低区间，中区间介于30%～60%的负荷峰值之间，高于60%的负荷峰值设为高区间。

2 供电路径辐射型空间确定

配电网的最优供电路径搜索实际上是对开关操作寻找一组最优的开关组合。考虑到实际配电网结构越来越复杂，开关数目增多，在重构过程中产生“组合爆炸”的问题概率增加，增加了解的冗余度。为了简化计算，提高智能算法的搜索效率，本文对搜索空间进行一定的缩减，得到规模相对较小的等效网络。以美国PG&E69节点系统为例，网络等效简化流程如图1所示，简化原则如下。

（1）为了避免孤岛的产生，不在环上的支路必须闭合，且在网络等效简化的过程中，可以视为重构无效支路，进行去除，如图1中圈出的支路。

（2）对于在环上的支路，若断开任意一个开关后，对供电效果影响一样的支路可以合并为一个等效支路组，且一个等效支路组内最多只能断开一个开关，如节点4和9之间的支路，可以合并为一个等效支路组。

等效简化的最终网络中，带圈的数字为等效支路组，共有12条，大大降低了编码空间，减少了重构过程中无效解的产生。其中，每个支路组有不同数量的支路构成，如等效支路组①={4-3,3-59,59-60, 60-61,61-62,62-63,63-64,64-65,65-66}，共有9条支路构成。

图1 网络等效简化流程Fig.1 Network equivalent simplification flow

对图1的最终等效网络进行编号整理，e代表树支（等同于闭合支路），L代表连支（相当于断开支路），且一系列的树支构成一组基本树（相当于供电路径），如图2所示，设其为连通图G。

图2 连通图GFig.2 Connected graph G

为了搜索连通图G的所有不同的树组，即确定配电网运行的所有辐射型供电路径解集空间，本文采用基于图论思想的无重复生成树策略[17]进行求解，具体过程如下。

（1）在连通图G中，选定一个参考树t0= (e1,e2,…,eN-1)，如图2实线部分，N为连通图G的节点总数。

（2）求出参考树t0所有割集，记为Sei(t0)，i= 1,2,…,N-1，并将Sei(t0)中不同于ei的支路设为ai（i=1,2,…,M -1，M为Sei(t0)中支路总数），分别替换t0中的树支ei，构成一组不同树的集合，记为Tei，表达式为

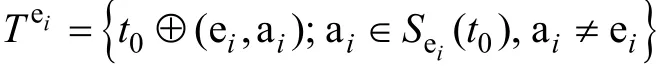
式中，⊕为异或运算符，符号两边比较元素相同结果为0，不同则为1。

（3）分别利用Tei的树t，求出包含支路ej的割集Sej(t)，其中，i＜j≤N-1。令bi∈Sej(t)∩Sej(t0)，即bi为Sej(t)和Sej(t0)的共有支路，i=1,2,…,L-1（L为Sej(t)∩Sej(t0)中支路总数），将bi分别替换t中的树支ej，得到一组不同树集合Teiej，即

（4）同理，按上述思想，分别交换参考树t0的N-1个树支得到一组包含不同树的集合Te1...eN-2eN-1，即

（5）综上所述，令k=1,2,…,N-1。当k=1时，求得的树集合为Te1, Te1e2, … Te1e2…eN-1；当k=2时，所求得的树集合为Te2, Te2e3,…, Te2e3…eN-1；依次类推，当k=N-1时，求得树集合为TeN-1；最后，按照上述无重复生成树策略，求得的连通图G所有无重复树集合为即分别对应不同的配电网辐射型网络结构，且不发生重复。

由此可见，在原始网络结构的基础上，结合网络等效简化和无重复生成树策略，使重构优化的搜索限定在辐射型供电路径集合中，无需再进行多次辐射型筛选校验，减少无效解的产生，节省了约束校验的时间。而且分布式电源的接入对辐射型供电路径空间生成也不会产生影响，通过该方法，提高了复杂有源配电网供电路径优化的快速性。

3 最优供电路径求解

求解配电网的最优供电路径即计算在不同的时序概率场景情况下满足重构优化模型的一组最优开关组合。本文利用两点估计法[18]计算配电网随机性潮流，并采用十进制编码策略，提出一种适于考虑随机性的配电网重构模型的改进教学优化算法，来求解等效支路组内的最优开关组合，即为所求的最优供电路径。

3.1 基于两点估计的概率潮流计算

电力系统随机性的潮流计算常用方法为概率潮流法。其中，蒙特卡洛仿真法因计算精度高，被广泛应用，但其计算量大，耗时长。而两点估计法不仅能够很好地克服上述缺陷，且精度较高，有利于提高不确定性潮流的计算效率[19]。

点估计法是通过给定随机变量概率分布的情况下，计算待求随机变量概率分布等结果。其中，两点估计法是点估计的一种，其基本思想是对有h个随机变量的系统，在每个随机变量左右邻域内寻找两个估计点，利用估计点求得离散分布的前3阶矩与待求量的前3阶矩相等原理，通过2h次确定性潮流计算，求得待求量的概率分布。

设各节点的注入量（有功功率、无功功率等）为Z=[zz…z]T，有h个随机变量，系统的待12h求量（节点电压幅值或网损等）可表示为S= F(z1z2…zh)，对每个随机变量zi，选取的两个估计点定义为

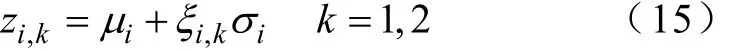
式中，i=1,2,…,h；μi、σi分别为随机变量zi的均值和标准差；ξi,k为位置度量，表达式为

式中，,3iλ为随机变量iz的偏度系数，表达的是随机变量与标准正态分布之间的偏差情况，计算式为

式中，E ■■(zi-μi)3■■为随机变量zi的三阶中心矩。

通过式（15）～式（17）求得两个估计点zi,k，代替zi，分别与其他随机变量的均值作为新的注入量，即(μ1,μ2,⋅⋅⋅,zi,k,⋅⋅⋅,μh)，进行牛顿-拉夫逊确定性潮流计算，就可求得待求量的两个估计值S(i,1)、S(i,2)，用wi,k表示zi,k概率集中度，可表示为

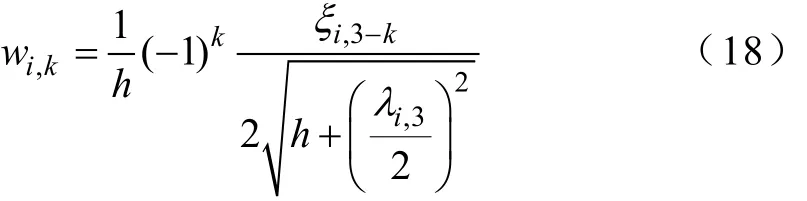
式中，wi,k∈(0,1)，且所有wi,k的和为1。则S的j阶矩可表示为

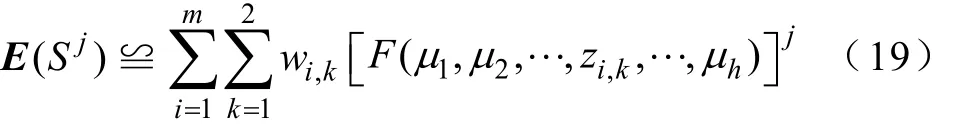
S的标准差可表示为

通过两点估计概率潮流计算，得到本文所需的各节点电压和网损概率分布函数。

3.2 基本教学优化算法

教学优化（Teaching Learning Based Optimization, TLBO）算法最初是由R. V. Rao等在2010年提出的一种群智能优化算法[20]。该算法分为“教”与“学”两个阶段，通过教师对学员的“教”和学员之间的相互“学”来提高班级的整体学识，即达到全局最优。TLBO具有参数少，算法简单，收敛速度快，精度高等优点[21]，已在求解配电网运行优化的问题中得到应用，并取得了较好结果。具体过程如下。

对于目标函数求极值，设一个班级随机生成NP个学员（搜索的粒子个数），任一学员为j=X，代表第j个学员，d为粒子的维数，代表第d门科目成绩。

（1）“教”阶段。在班级中，成绩最好的（适应值最好）学员作为教师，设为Xteacher，通过教师多次教学，来提高班级的平均成绩。“教”过程由Xteacher和学员平均值的差值以及教师的教学因子构成，由于每个学员的学习能力不同，随机地从教师处获取知识，即

（2）“学”阶段。该阶段指学员之间互相学习，通过两学员之间的差异进行学习调整，即

式中，ij≠，old()i fX为第i个学员的适应度值。

3.3 算法改进和最优开关组合确定

3.3.1 初始化编码

对于每个学员，即对应的每个粒子分别对应不同的网络拓扑结构，对粒子进行合理的编码，能减少编码空间，降低解的冗余度。因此，本文提出基于等效支路分组思想的十进制编码策略，具体编码原则如下。

（1）等效支路组数对应粒子维数。

（2）对每个等效支路组内的所有支路从1开始进行编码，粒子每维元素的编码代表相对应等效支路组内支路开关的状态，比如，粒子某维为0，代表该等效支路组内没有开关断开；粒子某维为l，代表该等效支路组内第l条支路断开，且l不大于该等效支路组内的支路数。

（3）每个等效支路组内最多只能断开一条支路。以图2等效简化拓扑为例，共有12条等效支路组，粒子的维数为12维，其产生的一组随机粒子为[0 4 1 0 0 0 0 0 1 5 7 0]，对应的等效支路组内开关状态为断开开关15-69、11-66、13-20、39-48、27-54，即断开所有的联络开关。若采用二进制编码策略，共有57条支路，则粒子的维数为57维。可见，基于等效支路分组思想的十进制编码策略，具有相对较小的解空间，有利于提高搜索效率。

3.3.2 TLBO算法改进

“教”阶段的教学因子决定着算法的搜索速度。“学”阶段，通过学生之间互相学习，保证算法的全局搜索能力。然而由于风机、光伏系统出力的变化性，原始算法有必要进行适当改进，来提高算法快速和全局搜索能力，更好地应用到复杂有源配电网供电路径的动态寻优中。

（1）引入自适应教学因子。在“教”的过程中，教学因子取值1或0，教学方法较为单一。表明学员在向教师学习的过程中，要么全盘接受，要么全盘否定。但在实际的学习过程中，学员根据自己的学习能力向教师学习，学习能力强则学习速度快；反之，则慢。尤其在学习前期，学员和教师之间水平差距较大，学习速度快，在接近教师水平时，学习速度逐渐变慢。教学因子TF决定平均值的改变，较大的TF会加快搜索速度，较小的TF会使搜索更加细微。因此，提出一种自适应教学因子，即随着迭代的进行，TF线性减小，即

式中，TFmax、TFmin分别为教学因子的最大、最小值；itermax为迭代的最大次数；iter为当前迭代值。

改进后的TF在前期较大，使搜索快速收敛于最优解附近，后期则采用精细搜索，以提高搜索的精度，从而能够动态、自适应地调整算法的搜索性能。

（2）增加“自习”阶段。在原始算法中，学员仅仅通过向教师和其他学员进行学习，使学员过度依赖他人，增加过早陷入局部最优的风险，本文引入“自习”机制，学习方法为

在充分利用“教”与“学”的基础上，引入自学机制后，学员的学习更加多样化，减小了学员对其他个体的依赖，增强了全局的搜索能力，避免过早地陷入局部最优。

因此，复杂有源配电网最优供电路径寻优的过程如下。

（1）初始化配电网络和算法参数，输入风机、光伏以及负荷的接入数据。

（2）根据风机、光伏随时间出力特性以及负荷需求，确定场景以及出现的概率。

（3）根据简化的配电网络，利用无重复生成树策略，生成不同的辐射状网络结构，即对应不同的班级学员，进而确定初始种群数。

（4）初始化编码，采用两点估计法进行潮流计算，计算适应值，找到当前班级中学识最高的学员，并设定为教师Xteacher。

（5）计算班级的平均值，进行“教”阶段，利用式（21）、式（22）、式（24）进行教学，若“教”后，学员的学识提高，则更新学员位置；否则，放弃本次“教”过程。

（6）进行“学”阶段，学员Xi和从班级中随机选取的一个学习对象jX，按式（23）计算适应值，若学员学识提高，则更新学员位置，否则，放弃本次“学”过程。

（7）进行“自学”阶段，按式（25）、式（26）进行自我学习，若学员学识提高，则更新学员位置；否则，放弃本次自学过程。

（8）验证是否达到最大迭代次数，是，则输出最优适应值，确定当前最优重构方案；否则，转步骤（4）。

综上所述，本文针对复杂有源配电网供电路径快速寻优的具体流程如图3所示。

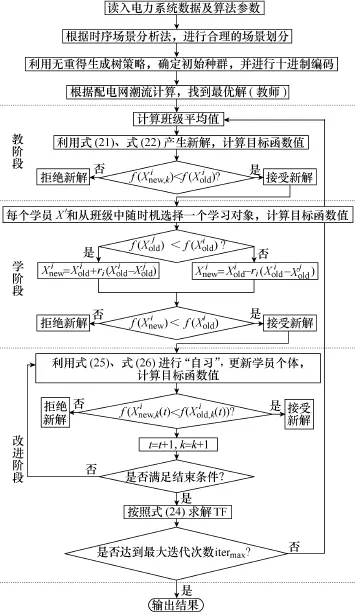
图3 优化流程Fig.3 Optimization flow chart

4 算例分析

为了更好地验证本文方法对于含风机和光伏接入的复杂有源配电网最优供电路径搜索具有快速性，本文采用图1中PG&E69节点配电系统[22]进行分析。该系统共接入48个负荷，负荷随机变量均值为节点系统的负荷值，标准差取其负荷值的10%。分别在节点10、27、68处并入三台额定功率为200kW、丹麦Bonus 1MW/54型风机；在节点34、52、56处接入Pilkington SFM144Hx250wp型太阳能光伏阵列四个，详细参数参考文献[23]。本文采用的风速和光照强度数据通过Home软件对上海地区（纬度31.08°N，经度121.35°E）月平均值进行模拟，得到以一天为例，按照前文时序场景划分的方法。根据负荷和风电、光伏的接入情况划分为6个场景，见表1。各场景的权重值分别为发生各场景的时间值与一天24h的比值。例如，场景一的权重=6h/24h=1/4。采用本文所提出的方法进行网络供电路径的优化，其中0代表不含风机、光伏接入的情况；1代表风机、光伏接入的情况。最低节点电压为95%置信度下节点电压的最低置信区间下限，结果见表2和图4所示。

表1 各时段内负荷和风电、光伏接入情况Tab.1 Scenery access of load, wind power and photovoltaic in each period

表2 PG&E69节点开关组合优化前后比较Tab.2 Comparison of the PG&E69 node switch combination before and after optimization

通过结果分析可以得出，在重构前，风机、光伏的接入可以适当地降低系统中网络损耗，并且改善网络节点电压分布；重构后，在95%置信度下，有功网损的概率置信区间为[77.84, 82.71]，系统网损总期望值由194.89kW降低至80.53kW，网损下降幅度为58.68%，且最低节点电压标幺值由0.96(pu)提高至1.018(pu)，系统运行的经济性和可靠性得到了提高。

图4 重构前后网损累积概率分布Fig.4 Cumulative probability distribution of network loss before and afer reconfiguration

重构后各时段节点电压分布如图5所示，由于风机、光伏出力随时间变化的特性，导致在不同场景下，电压分布不同。根据不同场景出现的概率进行电压加权平均并与重构前电压进行对比，如图6所示。可以发现，重构后，节点电压分布均衡，波动小，更加有利于系统平稳的运行。

图5 重构后各时段节点电压分布Fig.5 Voltage distribution of nodes in each time period after reconfiguration

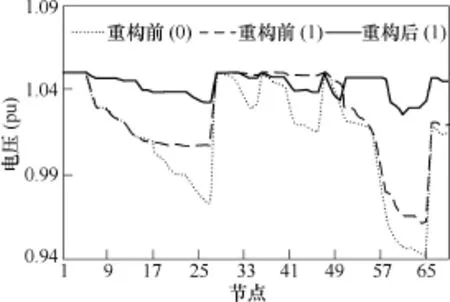
图6 重构前后电压期望值Fig.6 Expected voltage value before and after reconfiguration

为了证明本文方法在最优供电路径搜素上具有快速性特点，将本文配电网供电路径优化方法与文献[24]的遗传算法、文献[25]的二进制粒子群算法、文献[21]的教学优化算法进行对比分析。每种方法分别运行50次，最大迭代次数设为50，并各自选取其中进化效果最好的一组进行对比分析，结果如图7所示。

图7 各算法进化特性Fig.7 Evolutionary characteristics of various algorithms

由图7可见，本文所述的方法在搜索寻优过程中，迭代收敛次数少，能快速收敛到最优解，效率较高。

为证明所提出的搜索方法应用于复杂有源配电网供电路径快速寻优的普遍性，需进行平均性测验。将上述50次的运行结果进行对比分析，比较内容包括网损最优值、方均差、最小迭代次数、平均耗时和寻优率。其中，最小迭代次数指收敛到最优解的最小迭代次数，寻优率是收敛到最优解次数与实验总次数比值，结果见表3。

表3 不同方法的数据比较Tab.3 Comparison of different methods

通过表3可以得出，采用本文方法计算的方均差最小，寻优率最高，证明相对于其他方法，本文方法具有良好的稳定性。在50次的计算结果中，本文方法平均耗时为7.3s，在比较的方法中时间最短，说明其在寻优过程中具有明显的快速性。各方面指标测试表明本文方法在供电路径搜索上具有一定的数据优势，有力地说明了本文搜索方法收敛程度快，寻优时间短，效率高，误差低，具有优良的运行稳定性。

5 结论

本文面向复杂有源配电网最优供电路径的快速搜索，为了达到快速寻优的目的，在搜索过程中采取多方面、多阶段优化，主要结论如下：

1）基于时间尺度的风机和光伏的分场景随机性模型能够有效地分割出力的波动性，同时具有相对较高的准确度，符合工程实际，体现了对分布式电源随机出力的适应性。

2）简化复杂网络，并利用无重复生成树策略使搜索限定在辐射型空间中，可以避免大量无效解产生，无需再进行辐射型校验，有效缩短配电网供电路径寻优的计算时间，体现了当今复杂有源配电网供电路径寻优的快速性要求。

3）引入十进制编码策略来减少编码的冗余度，并对教学优化算法进行改进，不仅加快了动态寻优的搜索速度，而且提高了全局搜索能力，与传统方法相比，寻优效果具有一定的优越性。

综上所述，本文方法在应对含风机、光伏接入的复杂有源配电网最优供电路径搜索时，具有快速性和有效性，在未来的工程实际应用中，具有一定的指导意义，也为今后主动配电网优化运行提供了一定的理论依据。

[1] 靳小龙, 穆云飞, 贾宏杰, 等. 面向最大供电能力提升的配电网主动重构策略[J]. 电工技术学报, 2014, 29(12)： 137-147. Jin Xiaolong, Mu Yunfei, Jia Hongjie, et al. An active reconfiguration strategy for distribution network based on maximum power supply capability[J]. Transactions of China Electrotechnical Society, 2014, 29(12)： 137-147.

[2] Rao R S, Ravindra K, Satish K, et al. Power loss minimization in distribution system using network reconfiguration in the presence of distributed generation[J]. IEEE Transactions on Power Systems, 2013, 28(1)： 317-325.

[3] 李奔, 刘会家, 李珺. 考虑网络结构优化的含风电配电网多目标重构[J]. 电力系统保护与控制, 2015, 43(17)： 57-62. Li Ben, Liu Huijia, Li Jun. Multi-objective reconfiguration of distribution network with wind power generators considering network survivability[J]. Power System Protection and Control, 2015, 43(17)： 57-62.

[4] 蒲天骄, 刘克文, 陈乃仕, 等. 基于主动配电网的城市能源互联网体系架构及其关键技术[J]. 中国电机工程学报, 2015, 35(14)： 3511-3521. Pu Tianjiao, Liu Kewen, Chen Naishi, et al. Design of ADN based urban energy internet architecture and its technological issues[J]. Proceedings of the CSEE, 2015, 35(14)： 3511-3521.

[5] 张建华, 曾博, 张玉莹, 等. 主动配电网规划关键问题与研究展望[J]. 电工技术学报, 2014, 29(2)： 13-23. Zhang Jianhua, Zeng Bo, Zhang Yuying, et al. Key issues and research prospects of active distribution network planning[J]. Transactions of China Electrotechnical Society, 2014, 29(2)： 13-23.

[6] 王佳佳, 吕林, 刘俊勇, 等. 基于改进分层前推回代法的含分布发电单元的配电网重构[J]. 电网技术, 2010, 34(9)： 60-64. Wang Jiajia, Lü Lin, Liu Junyong, et al. Reconfiguration of distribution network containing distribution generation units based on improved layered forward-backward sweep method[J]. Power System Technology, 2010, 34(9)： 60-64.

[7] 赵晶晶, 李新, 彭怡, 等. 基于粒子群优化算法的配电网重构和分布式电源注入功率综合优化算法[J]. 电网技术, 2009, 33(17)： 162-166. Zhao Jingjing, Li Xin, Peng Yi, et al. A comprehensive optimization algorithm for injection power of distributed generation and distribution network reconfiguration based on particle swarm optimization[J]. Power System Technology, 2009, 33(17)： 162-166.

[8] Wu Y K, Lee C Y, Liu L C, et al. Study of reconfiguration for the distribution system with distributed generators[J]. IEEE Transactions on Power Delivery, 2010, 25(3)： 1678-1685.

[9] De M B H D, De Souza B A. Distribution network reconfiguration using genetic algorithms with sequential encoding： subtractive and additive approaches[J]. IEEE Transactions on Power Systems, 2011, 26(2)：582-593.

[10] 李锰, 黄泽华, 曾业运, 等. 基于信息集成的配电网关键负荷保障[J]. 电工技术学报, 2014, 29(增刊1)： 481-485. Li Meng, Huang Zehua, Zeng Yeyun, et al. The security of the critical load in the distribution network based on information integration[J]. Transactions of China Electrotechnical Society, 2014,29(S1)： 481-485.

[11] 张涛, 史苏怡, 徐雪琴. 基于二进制量子粒子群算法的含分布式电源配电网重构[J]. 电力系统保护与控制, 2016, 44(4)： 22-28. Zhang Tao, Shi Suyi, Xu Xueqin. Distribution network reconfiguration with distributed generation based on improved quantum binary particle swarm optimization[J]. Power System Protection and Control, 2016, 44(4)： 22-28.

[12] 卢扬, 吴俊勇, 郝亮亮. 基于改进MOBPSO算法的含分布式电源的多目标配电网重构[J]. 电力系统保护与控制, 2016, 44(7)： 62-68. Lu Yang, Wu Junyong, Hao Liangliang. Multiobjective distribution network reconfiguration with distributed generations based on improved MOBPSO algorithm[J]. Power System Protection and Control, 2016, 44(7)： 62-68.

[13] 李振坤, 周伟杰, 钱啸, 等. 有源配电网孤岛恢复供电及黑启动策略研究[J]. 电工技术学报, 2015, 30(21)： 67-75. Li Zhenkun, Zhou Weijie, Qian Xiao, et al. Distribution network restoration and black start based on distributed generators[J]. Transactions of China Electrotechnical Society, 2015, 30(21)： 67-75.

[14] Kavousi-Fard A, Niknam T, Fotuhi-Firuzabad M. Stochastic reconfiguration and optimal coordination of V2G plug-in electric vehicles considering correlated wind power generation[J]. IEEE Transactions on Sustainable Energy, 2015, 6： 1-9.

[15] 曾博, 刘念, 张玉莹, 等. 促进间歇性分布式电源高效利用的主动配电网双层场景规划方法[J]. 电工技术学报, 2013, 28(9)： 155-163. Zeng Bo, Liu Nian, Zhang Yuying, et al. Bi-levelscenario programming of active distribution network for promoting intermittent distributed generationutilization[J]. Transactions of China Electrotechnical Society, 2013, 28(9)： 155-163.

[16] Bernardon D P, Mello A P C, Pfitscher L L, et al. Real-time reconfiguration of distribution network with distributed generation[J]. Electric Power Systems Research, 2014, 107(2)： 59-67.

[17] Mayeda W, Seshu S. Generation of trees without duplications[J]. IEEE Transactions on Circuit Theory, 1965, 12(2)： 181-185.

[18] Xing H, Cheng H, Zhang Y. Optimal coordination of intermittent distributed generation with probabilistic power flow[J]. Journal of Electrical Engineering & Technology, 2015, 10(6)： 2211-2220.

[19] 王晓龙. 基于两点估计法的电力系统概率潮流计算[D]. 太原： 太原理工大学, 2013.

[20] Rao R V, Savsani V J, Vakharia D P. Teachinglearning-based optimization： an optimization method for continuous non-linear large scale problems[J]. Information Sciences, 2012, 183(1)： 1-15.

[21] Sultana S, Roy P K. Optimal capacitor placement in radial distribution systems using teaching learning based optimization[J]. International Journal of Electrical Power & Energy Systems, 2014, 54(1)： 387-398.

[22] Meneses d Q P, Contreras J, Rider M J, et al. Contingency assessment and network reconfiguration in distribution grids including wind power and energy storage[J]. IEEE Transactions on Sustainable Energy, 2015, 6(4)： 1524-1533.

[23] 黄红程, 顾洁, 方陈. 基于无向生成树的并行遗传算法在配电网重构中的应用[J]. 电力系统自动化, 2015, 39(14)： 89-96. Huang Hongcheng, Gu Jie, Fang Chen. Application of undirected spanning tree-based parallel genetic algorithm in distributed network reconfiguration[J]. Automation of Electric Power Systems, 2015, 39(14)：89-96.

[24] Cebrian J C, Kagan N. Reconfiguration of distribution networks to minimize loss and disruption costs using genetic algorithms[J]. Electric Power Systems Research, 2010, 80(1)： 53-62.

[25] Yin S A, Lu C N. Distribution feeder scheduling considering variable load profile and outage costs[J]. IEEE Transactions on Power Systems, 2009, 24(2)：652-660.

（编辑 张洪霞）

Fast Optimization of Power Supply Route for
the Complex Active Distribution Network

Chi Jiyun1Wei Gang1Li Gongxin2Li Qinyu3Zhang Jiakun1
（1. Shanghai University of Electric Power Shanghai 200090 China 2. Fujian Electric Power Corporation Fuzhou 350000 China 3. Shanghai Municipal Electric Power Corporation Shanghai 200233 China）

The increasing complexity of network structure and the uncertainty of distributed generation wide access bring out the power supply route optimization issue in active distribution network. Traditional distribution network reconfiguration methods are hard to meet the rapidity requirements. For the output volatility of wind turbine and photovoltaic power, based on the construction of the probability model of the scene, outputting segmentation is carried out on time scale, and the complex search space is simplified by the trees generation method without duplications. It can avoid repetitive radiation calibration, and reduce the redundancy of the solution space. The model is solved by the improved encoding method and the modified teaching learning based optimization algorithm. The search speed and global optimization ability are improved. Examples demonstrate that the proposed method is fast and effective.

Distributed generation, complexity, network reconfiguration, the generation of trees without duplication, the modified teaching learning based optimization algorithm, fast

TM764

迟吉运 男，1990年生，硕士研究生，研究方向为含分布式电源的配电系统优化运行及故障恢复。

E-mail： jiyunchi@163.com

韦 钢 男，1958年生，教授，硕士，研究方向为电力系统运行分析与计算、新能源与电力系统规划等。

E-mail： wg5815@sohu.com（通信作者）

10.19595/j.cnki.1000-6753.tces.151769

上海绿色能源并网工程技术研究中心项目资助（13DZ2251900）。

2015-10-18 改稿日期 2016-04-26