考虑机侧变流器复杂热载荷特性的寿命评估

高 兵 陈民铀 杨 帆 邵伟华 伏 进

（1. 输配电装备及系统安全与新技术国家重点实验室（重庆大学） 重庆 400044 2. 国网重庆市电力公司电力科学研究院 重庆 401120）

考虑机侧变流器复杂热载荷特性的寿命评估

高 兵1陈民铀1杨 帆1邵伟华1伏 进2

（1. 输配电装备及系统安全与新技术国家重点实验室（重庆大学） 重庆 400044 2. 国网重庆市电力公司电力科学研究院 重庆 401120）

风电机侧变流器中绝缘栅双极型晶体管（IGBT）模块运行时承受着复杂的多时间常数特性热载荷，是风电系统中最为薄弱的环节之一。然而现有研究更多是简单选取工作点数据或者仅考虑稳态工况以及无法考虑外部环境的长期随机变化。因此，本文建立了一种能够综合计及IGBT模块热载荷的复杂时间常数特性影响的寿命评估模型。分析了实际风电场中不同时间常数热载荷的寿命消耗特点，以及风速分布与寿命消耗之间的关系。研究了不同气温等效方法对寿命评估的影响规律，最后通过实验验证了该方法的准确性。结果表明，双馈风机中低频周期热载荷造成的寿命消耗更为严重，占到整体寿命消耗的64.42%。基频周期寿命消耗与风速概率密度具有严重的不对称性，超过60%的IGBT模块寿命主要消耗在低概率密度的高风速区间。气温等效方法对基频周期热载荷影响可以忽略不计，而忽略气温波动将导致低频周期寿命消耗评估结果减小12.26%。

机侧变流器 热载荷 寿命消耗 气温波动

0 引言

随着风电装机容量和风机功率的快速增长，风机可靠性的重要性日益突出，并带来高维修成本问题。风电变流器作为风电系统中最为薄弱的环节之一，是整个系统稳定运行的重要环节。统计数据表明，超过50%的变流器系统故障均是由IGBT功率器件失效造成的[1]。尽管IGBT模块失效机理极其复杂，与多种因素相关，但热载荷仍然是IGBT模块失效的最主要因素之一[2,3]。IGBT模块由于各层材料热膨胀系数的不匹配，在交变温度应力作用下，容易发生焊料层疲劳和铝键合线脱落，造成器件失效。风电系统中，相对于网侧变流器，机侧变流器（Generator Side Converter, GSC）失效率更高，是现有研究重点[2]。机侧变流器热载荷产生来源众多，包括外部环境、风机机械惯性，电气系统等，难以简单的将IGBT模块承受的热载荷等效为某一特定的温度条件。例如，风速变化时间较为缓慢，一般为分钟，而器件换流产生的热载荷波动时间数量级为秒。上述因素使得IGBT模块承受的热载荷极其复杂，其热应力包含多个时间常数特性，难以采用统一的仿真步长计算器件寿命。同时为了准确评估IGBT模块寿命，应考虑特定区域的风速概况等外部环境，一般需要较长时期内（一年）的数据，因而带来海量数据问题，采样间隔选取过长或者过短都会影响计算精度和效率。因此，建立准确反映上述热应力的寿命模型具有重要意义。

目前已有一些文献针对IGBT模块在实际载荷下的寿命和可靠性开展了相关的研究，但是更多是短时间内人为选择的较为简单的工作点数据。然后简单地循环利用短时间数据来得到较长时期内的结果[4-8]，且较多仅仅考虑稳态工况或者某一时间常数热应力影响[9-13]。然而上述假设严重偏离变流器实际运行情况，不仅因为IGBT模块承受的热载荷不具有周期重复性，而是随着风速和环境温度随机改变。并且未计及IGBT模块承受的多个时间常数热应力。此外，现有研究仅仅利用寿命模型计算IGBT模块失效时间以及某一风电场中的失效率，并未研究IGBT模块的寿命消耗分布规律，而该信息更能直观表示不同载荷情况下IGBT模块的寿命消耗和失效机理，对器件设计和提高其可靠性更为重要。

按照热载荷产生来源和波动特性，可以将变流器承受的复杂热载荷分离为三个独立的热应力，分别为开关周期、输出周期（基频周期）和低频周期（风速波动）。开关周期热应力主要由IGBT模块开通、关断造成，热载荷值一般较小，对器件寿命消耗的影响可以忽略不计。输出周期热应力主要是由IGBT模块换相产生，与变流器的工作状态有关，时间周期数量级一般为秒。而低频周期热应力主要由外界风速导致，时间周期数量级一般为分钟。不同时间常数热应力对IGBT模块的影响也将不同，其热载荷特性、时间步长都不一样，因此需要分别计算上述热载荷造成的影响。

文献[4]分析了不同调制方式下的变流器可靠性，但是采样风速时间太短，且未考虑气温变化的影响。文献[11]基于多状态概率模型分析了直驱风机中变流器基频周期热载荷和不同风机参数下的可靠性。文献[12]分析了风速分布对基频周期结温波动的影响。文献[13]在评估不同电流控制方式对双馈风机变流器功率循环能力影响时，只考虑风速状况的影响。同样，文献[14,15]分析了考虑风速湍流作用下的风电变流器可靠性。文献[16]分析了通用变流器不同结构对应的可靠性差异，但变流器元件可靠性在不同运行环境中的差异并没有得到体现。文献[17-19]基于物理失效模型研究了短时间内外部环境参数变化对直驱风机变流器系统可靠性的影响。文献[20,21]分析了不同调制策略下的功率模块损耗规律，发现五段式DSVPWM可在一个工频周期内将开关次数减少三分之一，有效减少逆变器的开关损耗和提高器件寿命。由于现有研究更多考虑了单一热载荷或者简单工况下的变流器寿命和可靠性，不能准确反映机侧变流器承受的复杂热载荷情况。因此需要建立一种更为精确的、考虑IGBT模块多时间常数热应力的寿命评估模型。

在现有研究的基础上，为了准确计算机侧变流器复杂载荷条件下的寿命，本文建立了一种更为精确的IGBT模块寿命评估模型，该模型综合考虑了外部环境和变流器电气系统的影响。以实际风电场为例，分别分析了不同时间常数热载荷的寿命消耗特点，以及风速分布与基频周期寿命消耗的关系。通过实验验证了本文方法的准确性，并分析了气温波动对不同时间常数寿命消耗计算结果的影响规律。结果表明，低频周期热载荷对机侧变流器寿命消耗影响更为严重，且大幅值结温波动产生频次与寿命消耗比例存在严重不对称性。而风速分布与基频周期热载荷寿命消耗也存在类似的不对称性。不同的气温等效方法对不同时间常数热载荷寿命计算影响也存在差异，气温等效方法对基频周期热载荷寿命影响较小，而计算低频周期载荷寿命时必须计及气温波动的影响。

1 机侧变流器寿命评估模型

1.1 双馈风机输出特性

本文所研究的双馈风机拓扑结构如图1所示，其中风电变流器系统由风力发电机机侧变流器和电网侧变流器构成，两者均采用两电平结构。

图1 双馈风机拓扑结构Fig.1 Topology of doubly fed wind system

根据不同风况条件，双馈风力发电机组的输出功率特性可分三个不同阶段[22]，如图2所示。在AC段，通过最大功率跟踪算法，以获取最大的风能；而在转速恒定区CD段，通过变流器转矩和变桨控制策略，风机保持最高转速运行。在这两个阶段，风机输出功率与风速满足三次方关系，这两个区域内风机输出特性相似。在更高风速区域，发电机输出功率将保持恒定即功率恒定区，为图2中的DE段，主要通过系统控制的桨距调节起作用。同时根据发电机的运行特性，机侧变流器可运行在整流模式（BE段）和逆变模式（AB段），不同模式下其损耗和结温均存在差异。

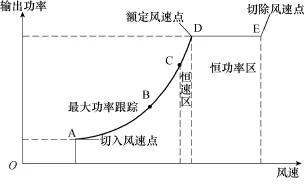
图2 双馈风机输出功率特性曲线Fig.2 Typical output power curve characteristics of doubly fed wind turbine generator system

1.2 机侧变流器IGBT模块结温计算

由于双馈风机机侧变流器输出频率较低，与IGBT模块热时间常数接近，采用开关周期损耗计算方法具有较高精度。同时调制方式对器件结温波动也存在影响[4,20,21]，为了避免调制方式带来的影响，本文主要研究了常规SPWM调制方式下机侧变流器的温度特性[12,23]。忽略一个开关周期内变流器输出电流的变化，机侧变流器IGBT模块与二极管开关一个周期内的功率损耗分别为

式中，Vce(d),25为IGBT（二极管）在25℃下的初始饱和压降；KV,igbt(d)为IGBT（二极管）初始饱和压降的温度系数；rce(d),25为IGBT（二极管）在25℃下的初始导通电阻；Kr,igbt(d)为IGBT（二极管）初始电阻的温度系数；Tj,igbt(d)为IGBT（二极管）结温；δk为占空比；Eon、Eoff分别为IGBT额定条件下的开、关损耗；fsw为开关频率；Ed,rr为二极管开关损耗；Udc为变流器直流侧电压；ic为器件导通电流；VN、IN分别为IGBT额定电压和电流；Kigbt(d),Tj为开关能量损耗温度参数，表示为

式中，Tj,igbt(d)为器件结温；ksw,T为温度系数。实际运行时，双馈风机机侧变流器中存在两个工作状态：励磁（逆变模式）和输出（整流模式），两者电流流通路径的不同导致IGBT模块损耗计算存在差异。具体差异体现在占空比上，逆变和整流模式下机侧变流器的占空比分别为

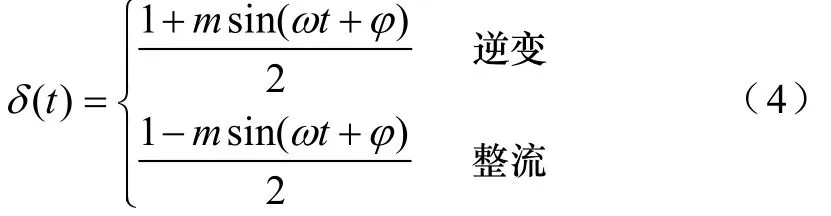
式中，φ 为交流电压与电流基波的相位差；m为调制比；ω 为调制波角频率。

IGBT模块热网络选取Foster热网络模型，结-壳热网络采用四阶模型，壳-散热器、散热器-环境均采用一阶Foster模型。机侧变流器IGBT与二极管的结温分别为

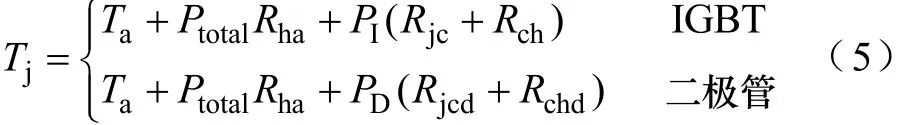
式中，Ta为环境温度；Ptotal为模块总损耗；Rha为散热器到环境之间的等效热阻；Rjc、Rjcd分别为IGBT、二极管到外壳的热阻；Rch、Rchd分别为IGBT、二极管外壳到散热器之间导热硅脂的热阻。上述取值均可根据datasheet获得。

1.3 机侧变流器多时间常数热载荷寿命评估模型

风机运行时，一般以某一采样间隔获得风速和气温数据，然后根据风机输出特性调整控制策略，实现风机的稳定并网运行。尽管在采样间隔内风速或者气温改变，但系统仍然按照采样参数控制风机运行，风机和变流器输出保持不变，而且风速波动一般较慢，IGBT模块的热时间常数通常为几秒，因此可以忽略IGBT模块结温暂态过程[24]。基频周期热载荷与变流器工作状态有关，而低频周期热载荷则与外界环境参数，如风速、气温有关。

文中利用最常用的Coffin-Mason-Arrhenius寿命模型，分别计算机侧变流器中IGBT模块因基频周期热载荷和低频周期热载荷造成的寿命消耗。该模型综合考虑了结温波动ΔTj和结温平均值Tm的作用。

式中，ΔTj、Tm分别为一个功率循环下的结温变化与平均值；Nf（Tm, ΔTj）为在ΔTj及Tm下的失效周期数；参量A、α 由实验数据拟合得到，文中分别为302 500、-5.039；Ea为激活能量常数，Ea=9.891× 10-20J；k为玻耳兹曼常数，k=1.38×10-20J/K。

以山东某风电场为例，考虑风机的切入和切出风速影响，本文所研究的风速区间为2～25m/s，利用所提出的方法计算IGBT模块的寿命，具体计算流程如图3所示，主要步骤如下。

图3 IGBT模块的多时间常数热载荷寿命计算流程Fig.3 Multi-time scale life calculation flow of IGBT module

（1）基于实际风速数据，并考虑风机的切入和切出风速影响，计算机侧变流器中IGBT模块的电参数，包括电压U、电流I、输出频率f0和占空比δ (t)。

（2）结合开关周期结温计算方法，计算IGBT模块的损耗和基频结温，并提取IGBT模块的低频周期载荷曲线，利用雨流算法统计基频和低频周期热载荷。

（3）利用寿命模型和线性损伤累积模型，分别计算基频周期和低频周期的寿命消耗，并分析各自寿命消耗特点。

2 机侧变流器IGBT模块复杂热载荷下的寿命评估

基于风电场实测风速和气温数据，按照如图3所示的评估流程计算IGBT模块寿命，并分析不同时间常数热载荷的寿命消耗规律，包括风速分布与基频寿命消耗的关系。

2.1 算例参数设置

本文所研究的双馈风机参数见表1，变流器中IGBT模块为SEMIKRON的SKM50GB12T4型。计算结温时等比例减小变流器功率[25]，根据datasheet手册[26]，表2给出了结温计算所需的IGBT模块损耗计算参数，且IGBT模块Foster热网络参数见表3。

2.2 机侧变流器的输出周期热载荷寿命评估

大量文献表明，机侧变流器载荷情况更为复杂，其失效率明显大于网侧变流器。因此本文主要研究双馈风机机侧变流器的不同时间常数寿命。选取的风电场风速以及气温数据如图4所示。

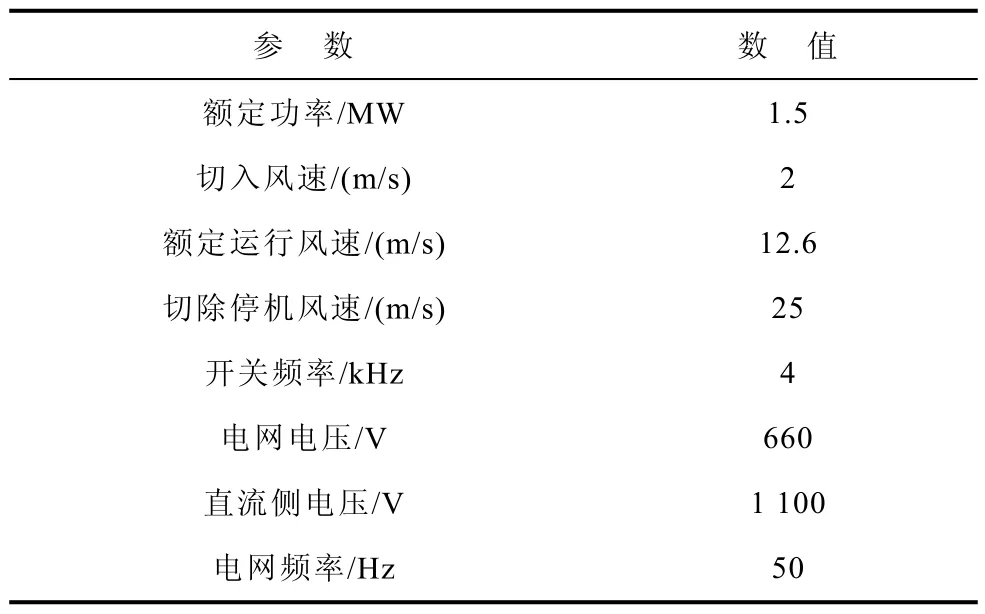
表1 双馈风机系统参数Tab.1 Parameters of doubly fed wind turbine generator

表2 IGBT模块损耗计算参数Tab.2 Parameters of IGBT module for power loss

表3 IGBT模块热网络参数Tab.3 Thermal network parameters of IGBT module

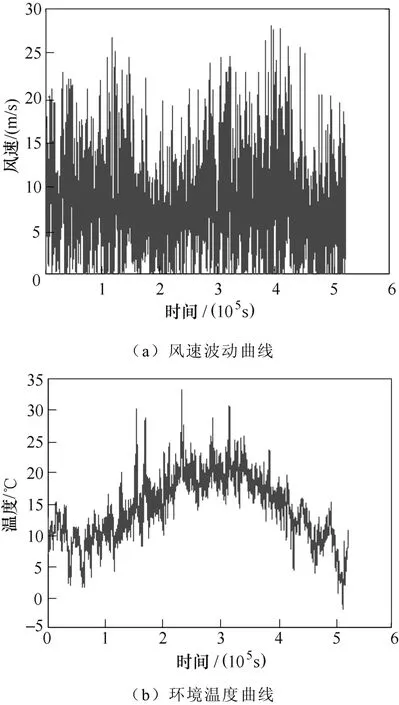
图4 风电场风速以及气温数据Fig.4 Data of wind speed and ambient temperature

目前计算风电变流器寿命时仅仅单纯针对某个风电场计算其平均失效时间（Mean Time To Failure, MTTF），并未针对风速分布对器件寿命的影响规律进入研究。目前有几种分布模型表示平均风速的变化规律，常用的两种为Weibull和Rayleigh分布，本文采用前者，其概率密度函数f (v)与年平均风速v的关系为

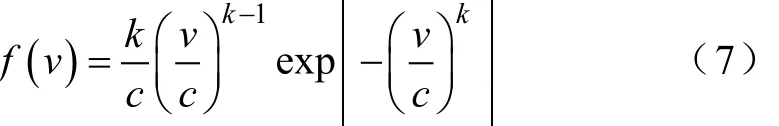
式中，k为形状参数；c为尺度参数。它们可以利用风电场年平均风速vaver和风速标准差σwind通过经验计算方程获取[27,28]，计算式为

该风场中年平均风速vaver=7.674 4m/s；标准差σwind=3.894 5；平均气温为14.1℃。而Γ为Gamma函数，按照风速概率密度计算公式，形状、尺寸参数分别为k=2.088 9、c=8.664 5。

在算例工况下，根据风速概率和寿命评估模型，得到了如图5所示的风速概率、寿命消耗以及累积寿命消耗之间的关系。可以发现，风速主要分布于低风速区间，说明机侧变流器大部分时间工作在低风速区域。然而寿命消耗曲线具有明显的波峰特性和不对称性，在同步转速点附近，寿命消耗最大，且高风速区域寿命消耗明显大于低风速区域。可以得出，机侧变流器寿命主要消耗在概率密度较小的大于或等于同步风速的高风速区域，这在寿命累积消耗曲线中也得到了验证。

图5 风速概率与器件累积寿命、寿命消耗变化规律Fig.5 Variation of accumulated life consumption, consumed life distribution and wind speed probability

为了进一步说明机侧变流器寿命消耗的不对称性，统计了大于或等于拐点风速vp的概率密度以及该风速区间内基频结温波动造成的寿命消耗比例p，见表4。

表4 风速概率及IGBT模块基频寿命消耗比例Tab.4 Relationship between wind speed probability and percentage of its life consumption of GSC

从表4中可以看出，在vwind＞vp的风速区间，风速分布概率为30.15%，而对应的寿命消耗比例却达到81.04%。因此，风速主要集中在低风速区间，而寿命主要消耗在vwind＞vp的风速区间。

为了进一步验证本文结论，以荷兰Lauwersoog、Valkenburg和爱尔兰Dublin三个风电场为例[11]，得到三个风电场中寿命消耗与风速关系如图6所示。

可以看出在三个风电场中出现了相同的规律，均是在同步转速点附近，机侧变流器寿命消耗最大，而寿命消耗主要集中在vwind＞vp风速区域，这也与图7所示的累积寿命曲线结论吻合。在图7中，不同风电场在高风速区间寿命消耗满足：山东风电场＞Lauwersoog＞Valkenburg＞Dublin，主要是因为上述风电场中年平均风速大小依次为山东风电场＞Lauwersoog＞Valkenburg＞Dublin，造成风电场中高风速概率密度也出现相同的规律。

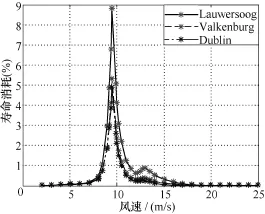
图6 机侧变流器寿命消耗分布曲线Fig.6 Life consumption with wind speed probability

图7 风速概率与器件累积寿命消耗的关系Fig.7 Relationship between accumulated life consuming and wind speed probability

表5定量给出了vwind＞vp风速区间对应的概率密度及其寿命消耗比例p。发现上述风电场中，在风速vwind＞vp风速区间，风速概率都很小，而对应的寿命消耗却均超过60%，尤其Dublin，风速概率只有7.5%，而寿命消耗比例却达到67.582%。因此针对高风速区间，可以采取不同于低风速区间的控制方法，如采用混合制开关频率、调制策略等。

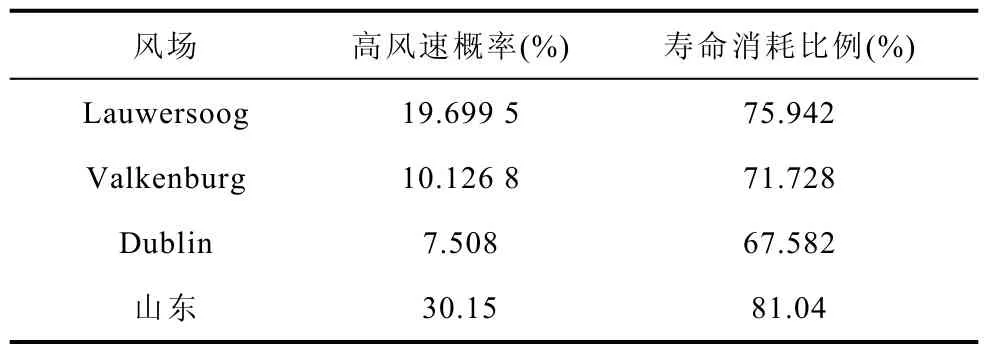
表5 高风速区域概率及对应的基频寿命消耗Tab.5 Probability density of high wind speed region and percentage of its lifetime consumption

2.3 机侧变流器的低频周期热载荷寿命计算

风机实际控制时一般按照采样风速控制系统，从而保证风机的稳定运行。而风速改变时将造成机侧变流器温度发生波动，导致IGBT模块承受较低波动周期的低频周期热载荷。低频周期热载荷反映了外界环境变化对变流器寿命的影响，与风速的随机波动和环境温度有关，具有随机性和不确定性。

本文以1min为采样间隔，一年中有超过52万个温度数据组。为了获取低频周期的温度应力曲线，首先对风速时序进行极点提取，判断最大极值点和最小极值点。对于最大极值点，取结温的最大值Tj,max为该风速下的风速温度；对于最小极值点，取结温的最小值Tj,min为该风速下的风速温度，这样就可以获取器件的低频结温。因此低频周期热载荷表征的是风电场中风速的时序性和波动程度。雨流算法作为目前最常用的数据统计算法，常用于温度曲线的统计。采用雨流算法对低频周期载荷曲线进行处理，可得到机侧变流器一系列离散数据信息，包括结温波动幅值ΔTj、结温平均值Tm以及波动次数N等，低频周期温度应力谱图如图8所示。

图8 低频周期温度应力谱图Fig.8 Thermal spectrum due to low frequency

从图8中可以看出，低频周期热载荷将产生大幅值结温波动ΔTj，尽管频次较小，其中ΔTj最大值为59.16℃。根据寿命公式可知，低频周期热载荷中的较低频次的大幅值ΔTj将带来较高的寿命消耗，明显不同于基频周期热载荷，其结温波动最大值为30～40℃。

为了定量分析风速随机波动对器件寿命的影响，表6给出了机侧变流器中出现的4种典型温度和风速波动循环以及寿命消耗，其中波动频次均为500次。

可以发现风速波动将产生大幅值的ΔTj，尤其是风速由同步风速增大到额定功率风速区域时，ΔTj幅值最为明显，IGBT模块寿命消耗最为严重。风速循环周期接近同步风速点时，IGBT模块将承受较大的热应力和较大的寿命消耗，主要因为在该点IGBT模块ΔTj较大。风速与低频周期结温波动分布规律如图9所示。图9给出了最大风速vmax与风速波动范围Δv与低频周期ΔTj的关系。当风速超过13m/s时，双馈风机输出额定功率，在该风速区，ΔTj较小，低频ΔTj几乎可以忽略，主要为基频ΔTj。

表6 风速波动对器件寿命的影响Tab.6 Effect of wind speed fluctuation on lifetime of IGBT

图9 风速与低频周期结温波动分布规律Fig.9 Wind speed and temperature variation profile

为了分析低频周期热载荷分布与IGBT模块寿命消耗之间的关系，表7给出了不同温度区间热载荷概率及低频寿命消耗比例。

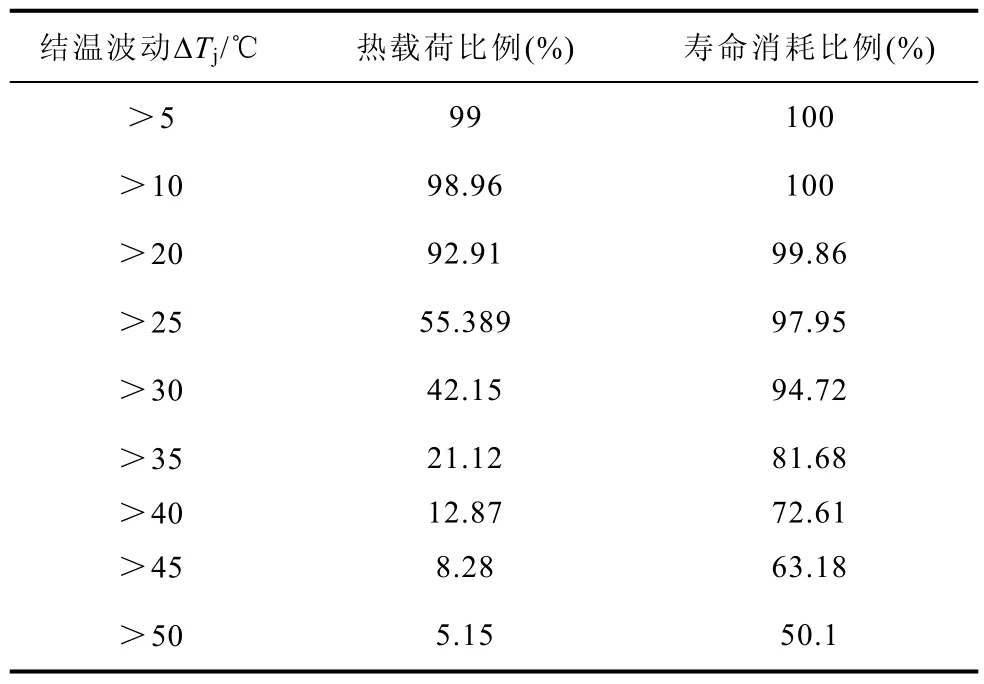
表7 不同温度区间热载荷概率及低频寿命消耗比例Tab.7 Probability of thermal loads and its percentage of low frequency temperature life consumption

从表7中可以发现大幅值热载荷在低频周期寿命消耗中占主要作用，尽管其概率较小。因此，低频周期热载荷寿命消耗与其概率严重不对等，这点与基频周期热载荷中风速概率与寿命消耗类似，但是两者存在一定的差异性。在基频周期中，寿命主要消耗在高风速区域，此时，结温波动较小，结温平均值较大。而在低频周期中，热寿命消耗分布相对较广，主要是因为低频周期热载荷与风速有关，风速随机波动，产生大幅值热载荷。然而ΔTj＜5℃的温度载荷对器件寿命消耗影响较小，几乎可以忽略不计。因此，可以从风机控制系统层面降低幅值较大的低频周期热载荷，从而提高器件可靠性。

综上所述，机侧变流器中上述两种时间常数热载荷应力特性具有明显差异性，对IGBT模块寿命的影响也不一样。表8给出了不同时间常数热载荷的寿命消耗。

表8 不同时间常数热载荷的寿命消耗Tab.8 Life consumption of different time scale thermal loadings

可以发现在双馈风机机侧变流器系统中，因低频周期热载荷造成的寿命消耗明显大于基频周期热载荷，其中低频周期热载荷导致的寿命消耗占到整体寿命消耗的64.42%。因此在双馈风机中低频周期热载荷是IGBT模块热失效的主要因素，且本文计算结果与文献[6]计算结果接近，在一定程度上验证了该方法的合理性。而研究表明，直驱风机中基频周期热载荷才是IGBT模块失效的主要因素，因此，两种不同风机需要减小的热载荷不同，导致控制策略也不一样。

尽管不同调制方式对器件结温波动存在影响[20,21]，其主要差异体现在损耗计算，但是基于SWPM调制方式的机侧变流器寿命评估方法同样可以适用于其他调制方式。

3 验证与分析

3.1 IGBT模块热响应行为验证

为了验证所提方法的准确性，最有效的方法就是获得运行变流器的失效统计数据。尽管已有关于变流复杂失效原因的研究，但是这些数据仅仅统计了变流器的失效次数和失效原因，并未详细给出失效类型及其相应的运行寿命。同时热失效只是变流器失效的主要因素之一，IGBT模块失效还包括其他失效因素如电气老化、湿度、振动、紫外辐射等，难以直接采用目前失效统计数据验证本文寿命模型。

然而现有一些文献研究结果可以论证本文得到的结论，文献[13,29]指出风电变流器在同步转速附近具有较大的寿命消耗，这点与图5得到的结论一致。而文献[5]指出基频周期幅值结温波动的影响不容忽视，这也与基频周期热载荷寿命消耗研究结论一致。文献[12,15]指出风速波动会产生较大幅值结温波动，导致IGBT模块可靠性降低，这与图9和表6结论吻合。热应力作为IGBT模块中主要失效因素，其与器件运行条件密切相关。因此，可以通过分析IGBT模块运行工况下的不同时间常数热载荷的温度行为来验证所提模型，因为这是研究思路的关键假设。

采用红外成像方法测量IGBT器件结温，其热响应行为测试平台如图10所示。为避免变流器控制策略对结温Tj测量的影响，变流器采用PWM开环控制。利用调压器和直流电容为IGBT模块提供输入电压，负载为电阻性，为两条10Ω支路并联而成。利用LC滤波器进行滤波，实验平台参数见表9。

图10 IGBT模块热响应行为测试平台Fig.10 Configuration of experiment setup for thermal behaviors validation

同时为了观察不同运行工况下IGBT模块壳温变化情况，采用K型热电偶实时测量IGBT和二极管芯片底部的壳温。热电偶直接固定在IGBT模块壳底部，正对着IGBT和二极管芯片中心点，并通过导热硅脂与散热器紧密连接。为了保证采样精度，采样帧频设置为400Hz，利用示波器监测变流器电气输出参数，包括负载电阻电压和电阻单支路电流，图11给出了实验平台中IGBT模块的电气输出参数。

表9 实验平台参数Tab.9 Parameters of experimental setup

图11 IGBT模块的电气输出参数Fig.11 Electrical output parameters of IGBT module

图12给出了输出周期下IGBT芯片结温和壳温的变化规律，可以发现在该输出频率为0.2Hz下，当达到稳态后，结温近似恒定波动，波动幅值为15.65℃，从而验证了所研究的输出周期热应力特性。

图12 IGBT模块热载荷曲线Fig.12 Thermal behavior validation of IGBT module

表10给出了不同输出频率f0下IGBT模块的结温波动，可以发现输出频率越小，结温波动越大。对于双馈风机，在同步转速点附近，其输出频率较低。因此，在该工作区间IGBT模块结温波动较大，器件失效概率较高，寿命消耗也最为严重，这与结论一致，进一步验证了该方法的准确性。

表10 不同输出频率下的器件结温波动Tab.10 Temperature fluctuation of different output frequency

而考虑风速影响时，在同步风速转速点附近，机侧变流器输出频率很低，假设为0.1Hz。当开关频率为2kHz时，实验测得结温波动为17.2℃，温度最大值为57.2℃，最小值为40℃。如果在此工作状态下，风速随机波动，风机运行在另一工作状态，假定为接近额定工作状态，该工作状态下结温最大值Tj,max可达到71℃，温度变化达到31℃，明显大于同步转速点附近的结温波动17.2℃。图13给出了风速随机波动造成的热载荷曲线，其中电流和输出周期按照实际风速序列改变。

图13 低频周期下的IGBT模块热载荷实验结果Fig.13 Experiments results of low frequency thermal behaviors of IGBT module

从图13中可以发现，风速波动将造成IGBT模块承受较大的热载荷，且波动规律与负载和风速变化规律一致。而图13c线圈中区域，结温波动尤其明显，因为该时刻为风机由同步转速点附近区域跳转到接近额定输出，这也与图9中结果一致，进一步说明了本文计算方法的准确性。同时风速波动造成的热载荷幅值明显大于基频周期热载荷，说明在机侧变流器中，低频周期热载荷造成的寿命消耗占主要作用，这点也与结论吻合。

3.2 气温的影响

考虑IGBT模块运行工况时，为了节省计算机资源，计算器件结温时一般将散热器温度等效为环境温度年平均值，从而忽略了环境温度波动的影响。从热载荷应力时间常数角度分析，该处理方法对基频结温波动影响较小，因为基频周期结温波动与变流器工作状态有关，两者时间常数差异较大，在基频周期内环境温度波动较小。但是气温波动周期与低频周期相近，可以等效为与低频热载荷周期相近的温度交变，忽略气温波动将对低频周期寿命计算造成较大的影响。为了验证理论分析的准确性，本文对比分析了实际气温时序和年平均气温方法的IGBT模块寿命计算结果。风电场年平均气温为14.1℃，对于低频周期热载荷寿命消耗，采用年平均气温方法得到的结果为24.26%，明显小于考虑气温实时序的27.776%，减小幅度达到12.66%。而基频周期热载荷寿命消耗只是略微减小为15.18%，较实际气温时序的15.34%，减小了1.04%。因此，可以采用年平均气温等效方法计算基波周期热载荷造成的寿命消耗；而对于低频周期热载荷需计及实际气温波动序列影响，即必须考虑环境温度波动的影响。

4 结论

针对难以准确评估双馈风机机侧变流器复杂热载荷条件下的寿命，基于热载荷的不同时间常数特性，建立了机侧变流器的多时间常数寿命评估模型。以实际风电场为例，分别分析了不同时间常数热载荷寿命消耗的特点以及风速分布与寿命消耗的关系，并通过实验验证了该方法的准确性。研究了气温波动对不同时间常数寿命计算结果的影响，得到了以下结论：

1）基频周期寿命消耗与风速概率密度具有严重的不对称性，IGBT模块寿命主要消耗在概率密度较小，而大于同步转速风速的高风速区域。

2）低频周期热载荷将产生大幅值结温波动，在低频周期寿命消耗中占主要作用，且ΔTj＜5℃的热载荷对低频周期寿命消耗的影响可以忽略不计。

3）相对基频周期热载荷，低频周期热载荷对IGBT模块寿命消耗更为严重，造成超过64%的整体寿命消耗。

4）气温波动对低频周期寿命消耗计算影响较大，采用年平均气温法将导致其计算结果减少12.66%，而对基频周期寿命消耗影响较小，仅为1.04%。

基于所建立的寿命评估模型，更能精确计算不同因素对风电变流器寿命和可靠性的影响，有助于从不同系统层面研究变流器寿命改善方法和措施。

[1] 黄玲玲, 曹家麟, 符杨. 海上风电场电气系统现状分析[J]. 电力系统保护与控制, 2014, 42(10)：147-154. Huang Lingling, Cao Jialin, Fu Yang. Review of electrical systems for offshore wind farms[J]. Power System Protection and Control, 2014, 42(10)： 147-154.

[2] 王春雷, 郑利兵, 方化潮, 等. 键合线失效对于IGBT模块性能的影响分析[J]. 电工技术学报, 2014, 29(增1)： 184-191. Wang Chunlei, Zheng Libing, Fang Huachao, et al. Analysis of the performance effect with bonding wires lift-off in IGBT modules[J]. Transactions of China Electrotechnical Society, 2014, 29(S1)： 184-191.

[3] 郑利兵, 韩立, 刘钧. 基于三维热电耦合有限元模型的IGBT失效形式温度特性研究[J]. 电工技术学报, 2011, 26(7)： 242-246. Zheng Libing, Han Li, Liu Jun. Investigation of the temperature character of IGBT failure mode based on 3D thermal-electro coupling FEM[J]. Transactions of China Electrotechnical Society, 2011, 26(7)： 242-246.

[4] Isidori A, Rossi F M, Blaabjerg F. Thermal loading and reliability of 10MW multilevel wind power converter at different wind roughness classes[C]//The 14th Annual IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, 2012： 2172-2179.

[5] Weiss D, Eckel H G. Comparison of the power cycling stress of IGBT in DFIG and full size converter for wind energy applications[C]//The 16th European Conference on Power Electronics andApplications, Lappeenranta, 2014： 1-9.

[6] Wang H, Ma K, Blaabjerg F. Design for reliability of power electronic systems[C]//IEEE 38th Annual Conference on Industrial Electronics Society, Montreal, 2012： 33-44.

[7] Wang H, Zhou D. A reliability-oriented design method for power electronic converters[C]//Applied Power Electronics Conference and Exposition (APEC), Long Beach, 2013： 2921-2928.

[8] Senturk O S, Munk-Nielsen S, Teodorescu R. Electro-thermal modeling for junction temperature cyclingbased lifetime prediction of a press-pack IGBT 3 L-NPC-VSC applied to large wind turbines[C]// Energy Conversion Congress and Exposition, Phoenix, 2011： 568-575

[9] Arifujjaman M, Iqbal M T, Quaicoe J E. Reliability analysis of grid connected small wind turbine power electronics[J]. Applied Energy, 2009, 86(9)： 1617-1623.

[10] Fuchs F，Mertens A．Steady state lifetime estimation of the power semiconductors in the rotor side converter of a 2MW DFIG wind turbine via power cycling capability analysis[C]//The 14th European Conference on Power Electronics and Applications, Birmingham, 2011： 1-8.

[11] Xie Kaigui, Jiang Zefu, Li Wenyuan. Effect of wind speed on wind turbine power converter reliability[J]. IEEE Transactions on Energy Conversion, 2012, 27(1)： 96-104.

[12] 杜雄, 李高显, 刘洪纪, 等. 风速概率分布对风电变流器中功率器件寿命的影响[J]. 电工技术学报, 2015, 30(15)： 109-117. Du Xiong, Li Gaoxian, Liu Hongji, et al. Effect of wind speed probability distribution on lifetime of power semiconductors in the wind power converters[J]. Transactions of China Electrotechnical Society, 2015, 30(15)： 109-117.

[13] Wei Lixiang, Kerkman R J, Lukaszewski R A, et al. Analysis of IGBT power cycling capabilities used in doubly fed induct ion generator wind power system[J]. IEEE Transactions on Industry Applications, 2011, 47(4)： 1794-1801.

[14] 季海婷. 计及温度变化因素的风电变流器可靠性评估[D]. 重庆： 重庆大学, 2014.

[15] 李辉, 秦星, 刘盛权, 等. 双馈风电变流器IGBT模块功率循环能力评估[J]. 电力自动化设备, 2015, 35(1)： 6-12. Li Hui, Qin Xing, Liu Shengquan, et al. Assessment of power cycling capability for converter IGBT module of DFIG system[J]. Electric Power Automation Equipment, 2015, 35(1)： 6-12.

[16] Aten M, Towers G, Whitlry C, et al. Reliability comparison of matrix and other converter topologies[J]. IEEE Transactions on Aerospace & Electronic Systems, 2006, 42(3)： 867-875.

[17] Wang H, Liserre M, Blaabjerg F, et al. Transitioning to physics-of-failure as a reliability driver in power electronics[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(1)：97-114.

[18] HuiHuang P, Mawby A. A lifetime estimation technique for voltage source converters[J]. IEEE Transactions on Power Electronics, 2013, 28(8)： 4113-4119. [19] Kostandyan E E, Ma K. Reliability estimation with uncertainties consideration for high power IGBTs in 2.3MW wind turbine converter system[J]. Microelectronics Reliability, 2012, 52(9)： 2403-2408.

[20] 何湘宁, 吴岩松, 罗皓泽, 等. 基于IGBT离线测试平台的功率逆变器损耗准在线建模方法[J]. 电工技术学报, 2014, 29(6)： 1-6. He Xiangning, Wu Yansong, Luo Haoze, et al. Quasi-online modeling method of the power inverter losses based on IGBT offline test platform[J]. Transactions of China Electrotechnical Society, 2014, 29(6)： 1-6.

[21] 张桂斌, 徐政. 最小开关损耗VSVPWM技术的研究与仿真[J]. 电工技术学报, 2001, 16(2)： 34-40. Zhang Guibin, Xu Zheng. Study and simulation of minimum switching losses VSVPWM technique[J]. Transactions of China Electrotechnical Society, 2001, 16(2)： 34-40.

[22] 赵霞, 王倩, 邵彬, 等. 双馈感应风力发电系统低电压穿越控制策略研究及其分析[J]. 电力系统保护与控制, 2015, 43(16)： 57-64. Zhao Xia, Wang Qian, Shao Bin, et al. Low voltage ride through control strategy and its analysis of doubly fed induction generator[J]. Power System Protection and Control, 2015, 43(16)： 57-64.

[23] 唐勇, 汪波, 陈明, 等. 高温下的IGBT可靠性与在线评估[J]. 电工技术学报, 2014, 29(6)： 17-23. Tang Yong, Wang Bo, Chen Ming, et al. Reliability and on-line evaluation of IGBT modules under high temperature[J]. Transactions of China Electrotechnical Society, 2014, 29(6)： 17-23.

[24] Arco S D, Undeland T M, Bohlländer M, et al. A simplified algorithm for predicting power cycling lifetime in direct drive wind power systems[C]// IEEE International Multi-Conference on Systems, Signals and Devices, Chemnitz, 2012： 1-6.

[25] Bowerman B L, O'Connell R T. Forecasting and time series： an applied approach[M]. London： Duxbury Press, 1993.

[26] Semikron IGBT module datasheet, SKM50GB12T4 [EB/OL]. http：//www.semikron.com.

[27] Gokcek M, Bayulken A. Investigation of wind characteristics and wind energy potential in Kirklareli Turkey[J]. Renewable Energy, 2007, 32(10)： 1739-1752.

[28] 李岩松, 郭世繁, 任国威, 等. 双馈式风力发电系统的机电暂态建模与运行分析[J]. 电力系统保护与控制, 2013, 42(13)： 104-109. Li Yansong, Guo Shifan, Ren Guowei, et al. Modeling and operation simulation of doubly-fed type wind power generation system electromechanical transient model[J]. Power System Protection and Control, 2013, 42(13)： 104-109.

[29] 赵燕峰. 风电变流器中IGBT的可靠性研究[D]. 成都： 西南交通大学, 2012.

（编辑 陈 诚）

Life Estimation of Generator Side Converter Considering the Comprehensive Mission Profiles

Gao Bing1Chen Minyou1Yang Fan1Shao Weihua1Fu Jin2
（1. State Key Laboratory of Power Transmission Equipment & System Security and New Technology Chongqing University Chongqing 400044 China 2. Electric Power Research Institute State Grid Chongqing Electric Power Company Chongqing 401120 China）

The insulated gated bipolar transistor (IGBT) suffers from complicated power loadings and is one of the weakest components in wind system. At present, researches mainly focus on a selected and tough operation environment in very short term or steady cases, taking no consideration on the long term variations of wind speed and ambient temperature. Therefore, a more detailed life consumption assessment model was built to evaluate the lifetime. Meanwhile, a wind energy conversion system was regarded as a case study. The characteristics of life consumptions under different time constant thermal loadings were discussed, as well as the relationship between wind speed probability density and life consumption. Furthermore, the influence of ambient temperature simplified methods on lifetime assessment was discussed. The experimental results indicate that the lifetime consumption caused by low frequency thermal loadings is dominant, which contributes to more than 64.42% of the wholelifetime. Variation of wind speed probability and fundamental frequency life consumption areserious unsymmetrical. More than 60% of life is consumed in high wind speed, which is with small probability density. Whereas different ambient temperature equivalent methods have great influence on different time constants thermal loadings. The ambient temperature fluctuation has little effects on fundamental frequency life consumption, which may induce a decreasing of 12.26% for low frequency lifetime calculation.

Generator side converter, thermal loading, life consumption, temperature fluctuation

TM386

高 兵 男，1987年生，博士研究生，研究方向为新能源发电转换系统状态监测。

E-mail： 785208784@qq.com （通信作者）

陈民铀 男，1954年生，教授，博士生导师，研究方向为智能控制与建模、人工智能的工程应用及新能源发电转换系统的寿命评估。

E-mail： mchencqu@126.com

10.19595/j.cnki.1000-6753.tces.151590

国家重点基础研究发展计划（973计划）（2012CB25200），国家自然科学基金（51477019）和中央高校基本科研业务费（106112015CDJXY150004）资助项目。

2015-09-24 改稿日期 2015-12-01