电力电子系统中的功率脉冲时序组合与逻辑组合

陈凯楠 赵争鸣 袁立强

（清华大学电机系 电力系统及发电设备安全控制和仿真国家重点实验室 北京 100084）

电力电子系统中的功率脉冲时序组合与逻辑组合

陈凯楠 赵争鸣 袁立强

（清华大学电机系 电力系统及发电设备安全控制和仿真国家重点实验室 北京 100084）

从电力电子系统的底层脉冲组合理论出发，对功率脉冲时序组合与逻辑组合的概念、方法和实现进行总结提炼分析。针对功率脉冲纯时序组合的局限性，提出功率脉冲及功率脉冲序列的逻辑组合方法，并对其组合思路和应用场景进行分析归纳。由于基于不同脉冲逻辑组合思路的两种典型应用，即多电平技术和倍频策略，均可以有效提高系统变换性能，以电力电子功率放大器为分析对象，对二者的谐波特性和适用性进行对比分析，以此作为上述理论的一个分析应用实例。通过电力电子系统中脉冲组合方法论的研究，有助于从更为底层的角度对相关技术进行系统认识，从而延伸拓展出新的脉冲组合与实现方式，推动电力电子技术的发展。

脉冲时序组合 脉冲逻辑组合 倍频策略 谐波分析

0 引言

电力电子变换技术区别于模拟功率放大技术最为本质的特征之一，为前者的功率器件工作于开关状态。这使得单个功率半导体器件的输出波形只能呈现方波脉冲的形式。本文将电力电子系统中产生方波脉冲的一个基本单元称为一个“开关单元”，它可以由单个功率半导体器件构成，也可以由若干同步动作的开关器件串并联而成。为了利用方波脉冲合成所需的各种形式的波形，通常使开关单元随着时间的推移发出一组脉冲序列，通过该序列上所承载的调制信息，得到所需波形分量，例如最为常用的脉宽调制（Pulse Width Modulation, PWM）方式。此为电力电子系统中功率脉冲时序组合的概念：单一开关单元所产生的功率脉冲随着时间的推移而组合成为一条脉冲序列的过程。但随着电力电子系统功率等级、输出频率、波形质量以及功率密度等性能要求的不断提高，在现有器件水平下使用单纯的脉冲时序组合已难以满足需求，因此有必要引入功率脉冲逻辑组合的概念，其涵义为：不同开关单元按照一定组合规律，在同一时间段各自产生特定的功率脉冲或功率脉冲序列，并通过空间上的叠加组合，共同实现输出波形的合成。

实际上，上述时序组合的概念作为当今电力电子技术的基石之一，在几乎所有的电力电子变换器当中均有体现；而脉冲逻辑组合的概念，尤其是在效果上，也已出现在许多电力电子系统当中，例如多电平技术、交错并联技术等。但对于相关方法论层面的提炼归纳，以及对其进行深入分析与延伸拓展的研究却很少出现。文献[1]对电力电子系统中的功率脉冲进行过深入分析，其中也包含脉冲时序组合与逻辑组合的表述，但并未对其进行进一步的研究与阐述。文献[2]给出了一种多电平通用调制算法，其首先经由普遍适用的载波调制方法得出目标输出波形，之后再利用逻辑组合的思路，结合不同的拓扑与开关管状态，利用各开关器件所产生的脉冲序列组合叠加而形成所需输出波形。其直接从实现方法上（而不仅仅是最终效果上）体现了脉冲逻辑组合的思想，但该文献仅针对多电平变换器的一种调制方式分析，而没有针对这一通用的方法论进行归纳总结。

除了多电平技术以外，脉冲逻辑组合的另一个典型应用思路为本文所针对的倍频策略。该方法可通过不同开关单元之间的脉冲逻辑组合，使得变换器输出PWM频率为单个器件等效开关频率的数倍，进而达到提升波形质量、减小无源器件、拓宽工作频带等目的。实际上，某些多电平方法，例如基于载波移相调制的级联式多电平[3-5]，在输出波形方面同样可以达到类似倍频的效果，但其输出谐波特性与上述倍频策略不尽相同，因此应用场合也有所区别，下文将会对此进行具体分析。此外，感应加热电源领域也有类似的倍频策略研究，例如文献[6]给出了一种基于IGBT的倍频拓扑，通过负载、直流母线电感、桥臂以及桥臂间的换流支路构成特殊的换流模式，从而实现了输出频率为器件开关频率的2倍，但由于其谐振换流方式的特殊性，该拓扑仅适用于感应加热电源以及类似功能的变换器当中，且只能实现有限的2倍频。

由此可见，虽然从实现效果上来说脉冲逻辑组合的概念在现有的多种变换器当中均有所体现，但却缺乏对其普遍适用性方法论的提炼和分析；而对于由此引出的倍频思想，也同样缺乏对其系统性的研究，且独立于多电平的倍频策略在电力电子系统中的应用并不多见。

本文将首先从时域和频域的角度介绍功率脉冲时序组合的概念，并阐述其局限性，进而引出脉冲和脉冲序列的逻辑组合；在给出三种功率脉冲逻辑组合思路之后，结合现有调制策略对脉冲的纯逻辑组合以及脉冲序列的逻辑组合进行了归纳总结，并引出一种普遍适用的倍频策略；由于基于不同逻辑组合思路的两种方法，即多电平技术和倍频策略，均能有效提高变换器性能，但二者的具体特性又有所不同，因此本文从理想脉冲层面对二者的谐波特性及其适用性进行了深入对比分析，以此作为功率脉冲时序与逻辑组合理论的一个分析应用实例。

1 功率脉冲的时序组合及其局限性

为使论述更为清晰，本文将针对电力电子功率放大器作为分析对象进行论述。其区别于其他变换器的最大特点之一是输出波形的任意性，因此针对其进行脉冲组合的分析具有普遍适用性。

在时域上，电力电子功率放大器要求能够进行直流、正弦交流乃至特定频带内各种任意形式的功率波形变换；对应到频域上，其要求能够在特定的信号频段内，精确地控制各种所需频率分量，电力电子功率放大器典型输出波形频域图如图1所示。而对于信号频段外的频率分量，虽然从理论上来说可以不加控制，通过输出滤波器将其滤除，但实际上由于滤波器不可能具有完全理想的特性，并且出于降低滤波器设计实现难度、减少谐波和噪声对有效信号的干扰等因素的考虑，还是应当令其尽可能地远离信号频段并且减小其幅值。

图1 电力电子功率放大器典型输出波形频域图（滤波前）Fig.1 Typical spectrum of output waveform of power electronics amplifier (before filtering)

然而在电力电子系统中，若将一对互补开关视为如图2所示的基本拓扑单元，则在理想情况下其所能产生的基本波形单元仅为特定幅值和脉宽的方波脉冲，其数学表达式以及对应的频域展开式为

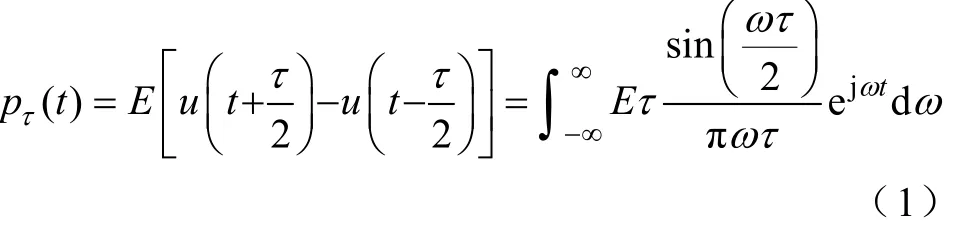
式中，E和τ 分别为脉冲的幅值和脉宽；u(t)为单位阶跃函数。由式（1）可得在不同脉宽下的频谱图如图2b所示，可见在单个方波脉冲中包含了所有频率分量，显然无法达到上述精确控制频率分量的目的。

图2 电力电子系统基本波形单元Fig.2 Basic waveform unit of power electronic system

对此，当前电力电子系统中最常用的方式是让一组互补开关以特定的时间间隔产生一组脉宽可调的脉冲序列，以此来合成所需要的波形，即PWM方式。该脉冲序列的数学表达式为

脉冲合成方式为引言所提到的脉冲时序组合。实际上除了PWM，包括脉冲密度调制（Pulse Density Modulation, PDM）在内的一些其他脉冲调制方式，也都属于脉冲时序组合的范畴。但因为PWM在电力电子系统中应用最为广泛，因此下文将主要针对此方式进行论述。

通过上述脉冲时序组合，可合成大部分所需频谱。以对称规则采样的正弦脉宽调制（Sinusoidal PWM, SPWM）为例，在去除直流分量后其脉冲序列的频谱表达式[7]为

其中

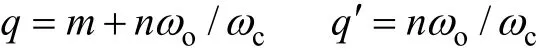
式中，ωo、θo以及ωc、θc分别为参考波和载波的角频率和相位；M为调制比；Jn(x)为x的n阶贝塞尔函数。假设参考波频率1kHz，载波频率20kHz，调制比0.9，则标幺化后的脉冲序列频谱图如图3所示。可以看出，只要滤除载波及其倍数次的谐波以及边带谐波（即图3b中信号频段以外的谐波），方可得到所需的正弦波形。当然，由于规则采样自身的特性使得在信号基波周围也产生了一些边带谐波，但其幅值相对较小，造成的波形失真程度有限。假如采用自然采样方式，则理论上可以将基波的边带谐波完全消除。

图3 PWM脉冲序列及其典型频谱（以对称规则采样SPWM为例）Fig.3 PWM pulse sequence and its typical spectrum (e.g. SPWM based on symmetric regular sampling)

然而，随着应用领域的不断拓宽，当对电力电子系统提出更高的性能要求时，单纯的脉冲时序组合方式将显现出其局限性。例如在电力电子功率放大器中，功率等级、输出频带和保真度作为三个重要性能指标，往往成为相互制约的因素。由图3b可以看出，考虑到所需波形的任意性，要保证输出波形质量（保真度），必须保证整个信号频段内足够“纯净”，即没有所需波形分量以外的谐波干扰。否则在信号频段内一旦出现了多余的谐波，是难以靠滤波手段来消除的。而在理想情况下（不考虑功率脉冲延迟与畸变等非理想因素），仅考虑脉冲调制层面（不考虑上层控制引入的谐波），信号频段内的谐波来源主要包括以下两方面。

（1）原始信号波形分量自身的边带谐波。这部分谐波主要由规则采样的自身特性所造成，除非采用自然采样，否则难以完全消除。好在通常其幅值并不大，而且随着PWM脉冲频率的升高，亦有降低的趋势。

（2）低次载波谐波的边带谐波。假如PWM脉冲频率不够高，则载波频率的左侧边带谐波，甚至2次、3次载波频率的边带谐波，都有可能会进入信号频段，从而带来谐波失真。

因此，要提高电力电子功放的输出频带并保证较高的保真度，应当采用更高的PWM脉冲频率，而对于纯时序组合，即单个开关单元所产生的脉冲序列来说，PWM脉冲频率就等于器件的开关频率。但在中大功率应用中，开关器件由于受到开关暂态时间、开关损耗以及电磁干扰等因素的影响，其开关频率往往受到限制。因此，如何在现有器件水平下同时提升功率等级、频带宽度和保真度成为电力电子功率放大技术的关键和难点所在。此外，提升PWM脉冲频率亦可降低无源滤波元件的体积和重量，是提高系统功率密度的主要途径之一。

2 功率脉冲及脉冲序列的逻辑组合

针对上述脉冲时序组合所遇的瓶颈，本文引入功率脉冲的“逻辑组合”概念：将多个基本开关单元所产生的功率脉冲或脉冲序列通过逻辑组合的方式进行空间叠加，以此对所需频率分量进行进一步合成。其目的在于突破现有器件有限的开关能力，以实现更高性能的电能变换。此处“有限的开关能力”包括了开关器件的电压、电流等级，开关速度限制等；而“更高性能的电能变换”则包括了更大的变换功率、更宽的输出频带、更好的波形质量以及更高的功率密度等。

需要指出的是，在电力电子技术几十年的发展过程中，脉冲的逻辑组合概念已在多种变换器当中有所体现，因此接下来的说明会对部分已有技术的逻辑组合概念进行提取和说明。但这一概念的提出，其意义不仅仅在于可以对已有的诸多拓扑和调制方式进行总结和归纳，更在于可以延伸拓展出新的思路和方法，从而推动电力电子技术的发展。

2.1 功率脉冲逻辑组合的三种思路

脉冲逻辑组合的具体实现方式及其衍生出来的各种拓扑和调制方法多种多样，从H桥的参考波倒相调制，到各种多电平变换器，乃至下文将要提到的倍频策略，都应用了各自的逻辑组合方法。但归纳起来，脉冲逻辑组合主要包括了三种思路，三种功率脉冲逻辑组合方式示意图如图4所示。

图4 三种功率脉冲逻辑组合方式示意图Fig.4 Illustration of power pulse logical combination methods

2.1.1 基于电平组合

该方式以得到更多的量化电平为目的，将若干子脉冲的电平相叠加，使得输出脉冲能更好地逼近所需波形并达到更高的电平值，从而达到减小谐波、降低器件耐压和du/dt等效果。其组合示意图如图4a所示（但不局限于此），其对应的数学表达式为

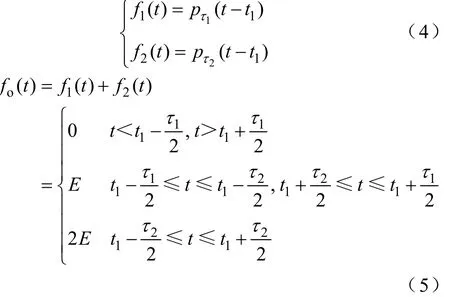
目前对于该方法的典型应用包括多电平变换器[8]、移相调制[9]以及多重化技术[10,11]等，根据不同的拓扑和调制方式，可以体现出不同的特点，对此难以一概而论。但其整体优势在于增加了一个调制自由度（电平），因此可以在对波形进行脉宽调制的同时也进行电平调制，使得输出脉冲波形包含更精确的调制信息，从而在有限的电压等级和开关频率下提高波形变换能力和波形质量。

2.1.2 基于脉冲组合

该方式以增加单位时间内输出的有效脉冲个数为目的，将若干子脉冲序列错位叠加，在不增加单个脉冲序列频率的情况下获取更高的输出脉冲频率，如图4b所示，其对应的数学表达式为

需要说明的是，相对于电平组合，该方式必须作用于脉冲序列，与PWM等脉冲时序组合方法结合使用方有意义，类似示意图中对单个脉冲进行错位叠加在实际应用中是几乎没有意义的。这种组合方式的本质是对脉冲时序组合的一种拓展，二者都是使用随时间轴展开的脉冲序列所携带的调制信息来对所需波形进行合成。但与纯时序组合相比，基于脉冲的逻辑组合将一个脉冲序列上的调制信号分摊给了多个脉冲序列，由于在实际实现中一个脉冲序列通常就对应着一对互补开关，于是这就减轻了每个器件的开关动作压力。

2.1.3 基于边沿组合

无论是时序组合还是上述两种逻辑组合方式，都是以单个脉冲作为波形合成的基本单元。而基于边沿组合方式则是将脉冲进一步拆分为上升沿和下降沿，即以边沿为基本单元，通过将若干个子“边沿序列”进行合理的叠加组合，从而合成所需的输出脉冲序列。其原理示意图如图4c所示，对应的数学表达式为

与基于脉冲的逻辑组合相同，通常情况下该组合方式本身也不包含调制信息，因此同样需要与脉冲时序组合结合使用。所不同的是，该方式将脉冲序列进一步拆分为边沿序列，其基本单元数量为原来的两倍，而在变换器中一个脉冲边沿实际上对应着一对互补开关的一次开关动作，因此可以对子序列，即互补开关单元的动作次序进行更合理地优化分配。例如将一个输出脉冲的上升沿和下降沿分别分配给两组互补开关完成，以此来控制换流通路以获得更好的瞬态效果，或是控制稳态电流通路以分摊通态损耗等。与上述基于脉冲的逻辑组合相同，该方式同样可以在相同的器件开关频率下增加输出脉冲的采样频率，同时还额外增加了开关动作的分配自由度。在实际应用中，将PWM和移相控制相结合的控制方式可利用该组合思路进行优化调制。

2.2 功率脉冲的纯逻辑组合

对基于脉冲组合和边沿组合的功率脉冲逻辑组合方式，由于其本身并不包含任何调制手段，因此必须作用于包含调制信息的脉冲序列（如PWM脉冲序列）才有实际应用价值，需要与脉冲时序组合结合使用。但对于基于电平组合的方式来说，其本身增加了一个独立的调制自由度（电平调制），因此在某些情况下可以独立应用于变换器中，对波形进行单独的电平调制，为功率脉冲的纯逻辑组合。

当输出波形在形状、幅值、频率等参数上较为固定，且对其波形理想程度要求不高时，可以舍弃PWM等脉冲时序组合方式，而完全通过脉冲的电平组合来得到输出波形（此处仅针对输出波形的单个周期范围界定是否包含脉冲的时序组合，因此对于因输出波形周期性重复而呈现的脉冲序列特征并不在此考虑范围内）。该方式的典型应用主要包括多重化技术，以及多电平中的方块开关（block switching）技术，其中前者为后者的一个特例。在多电平方块开关技术中，可以利用相同或不同幅值的子序列脉冲，通过控制其位置以及占空比，叠加逼近所需输出波形。对于该技术的脉冲组合以及谐波分析，文献[7]已详细给出，此处不再赘述。

2.3 功率脉冲序列的逻辑组合以及倍频策略

在当今对电力电子系统性能要求越来越高的情况下，往往需要同时使用脉冲时序组合与逻辑组合，方能获得更好的效果，即功率脉冲序列的逻辑组合。对于上述的三种逻辑组合方式，与时序组合相结合后可分别导出不同的脉冲合成策略。

基于电平的脉冲序列逻辑组合已在多种应用场合中得到了体现。例如H桥的参考波倒相调制就属于最简单的一种PWM脉冲时序与电平逻辑组合相结合的例子[12]。其利用两个桥臂所产生的脉冲序列进行叠加，使得输出电压波形具有三个电平值，同时也带来了输出电压脉冲频率加倍的效果（对于对称规则采样来说这种加倍效果所带来的好处甚微）。此外使用了脉宽调制的多电平变换器也属于此概念的典型应用之一。由于同时包含了电平和脉宽两重调制信息，通常可以获得更为理想的输出波形；同时由于可以利用若干子序列正向叠加来产生高输出电压，使得在相同的输出电压等级下，其单个功率脉冲序列的幅值可以更小，从而降低了器件耐压需求以及du/dt。因此该方式在大功率高性能变换器当中具有较大优势。

基于脉冲或边沿的脉冲序列逻辑组合为最典型、最直观的实现方式，接下来将引入的倍频策略。基于脉冲的逻辑组合的典型实现方式为：使用N倍频的载波对信号波形进行采样和脉宽调制，得出参考输出脉冲序列之后再将其以脉冲为单位分配给N条子脉冲序列，基于功率脉冲逻辑组合的倍频策略示意图如图5所示（以N=2为例）。由于在实际装置中一条子脉冲序列通常由一对互补开关产生，因此最终输出的PWM脉冲频率将是器件实际开关频率的N倍。这样便可在器件开关频率受限的情况下，突破第1节中所述的限制，达到拓展输出波形频带宽度，提高输出波形保真度的效果。

图5 基于功率脉冲逻辑组合的倍频策略示意图Fig.5 Illustration of frequency multiplication strategy based on power pulse logical combination

而基于边沿的脉冲序列逻辑组合是将图中的参考输出脉冲序列再拆分为上升沿和下降沿，并将这些边沿信号合理地分配到各子序列中去。当然，对于图中所示的两条子序列来说其分配的可选方式着实不多，但当采用更多子序列组合，并结合实际装置中各种因素的考虑时，则可以对其分配方式进行进一步的优化。

3 两种典型的功率脉冲逻辑组合技术对比分析

根据以上分析可以看出，在具体应用中，基于电平的逻辑组合通常引出的是各类多电平拓扑与调制策略，而基于脉冲以及边沿的逻辑组合引出的则以倍频策略为主。两种策略均有助于在有限的器件水平下提高系统变换能力，但二者的输出谐波特性却有所不同。在本文作为分析实例的电力电子功率放大器中，输出谐波特性直接关系到系统的工作带宽和波形保真度。因此本文将以此适用性为例，对二者的谐波特性进行详细的对比分析。

3.1 多电平调制方法定性分析

对于多电平策略，虽然有着各种不同的拓扑形式，但其底层的脉冲组合方式主要还是与调制方式有关，而其中最为常用，同时也较为适用于任意波形变换的，还是基于载波的调制方法。而多电平载波调制虽然也同样种类繁多，但大致上可以将其分为两大类：基于载波移相（Phase Shifted, PS）的方式，如图6a所示；基于载波分布（Carrier Disposition, CD）的方式，如图6b所示，例如APOD（alternative phase opposition disposition）、PD（phase disposition）以及POD（phase opposition disposition）等[7,13]，而其他各种策略多为两者的变形或混合。

包含CD的调制方式，是利用上下层叠的载波首先对参考波形进行了一次电平调制，之后再进行脉宽调制，因此与普通两电平变换器的纯脉宽调制相比，可以显著降低其谐波含量，提高保真度。其本质相当于让每对互补开关分别负责不同电平段的脉宽调制并产生对应的脉冲序列，之后将其进行叠加组合，得到最终输出波形。但也正因如此，该方式应用在功率放大器中具有较大的缺陷。大部分传统变换器在正常工况下，输出的波形幅值变化范围通常不大，且为了提高母线电压利用率，往往尽可能地保持高调制比，这使得上述电平调制的效果得以充分发挥。但对于功率放大器所面向的任意波形来说，却无法保证这一点，例如在音频信号中，信号的动态范围往往非常大，这意味着变换器需要在保证高幅值信号不过载的同时，也能够对低幅值的小信号波形进行高保真的还原。对应到图6c所示的载波调制中，对于持续的小信号，将只有一部分载波能够参与调制，这意味着用于电平组合的脉冲序列数量将大大降低，甚至完全脱离逻辑组合的效用而还原到普通两电平变换器的纯时序组合状态。这无疑将显著降低小信号波形输出的保真度。基于载波移相调制的电平组合策略在效果上与基于脉冲组合的倍频策略有相通之处，因此有必要进行详细分析，基于载波移相调制的脉冲产生和组合示意图如图7所示。由图7可以看出，无论是对于高幅值信号还是低幅值信号，载波移相调制的组合波形同样具有倍频的效果，尤其是对于低幅值信号来说，其脉冲序列的组合方式甚至与图5中基于脉冲的逻辑组合倍频方式完全一致。但由于二者对于单条脉冲序列中脉宽的决定方式不同（即调制方法不同），使得其最终输出谐波存在一定的差异。下面将对此进行具体分析。

图6 两类多电平调制策略示意图Fig.6 Two types of multi-level modulation strategy

需要说明的是，根据拓扑的不同，载波移相调制的输出波形最终并不一定表现为由移相载波所得出的脉冲序列的简单叠加，但由于此处探讨的重点为底层的脉冲序列产生与组合方式不同所造成的一般性谐波特性差异，因此仅对图7所示的脉冲序列组合情况进行研究。

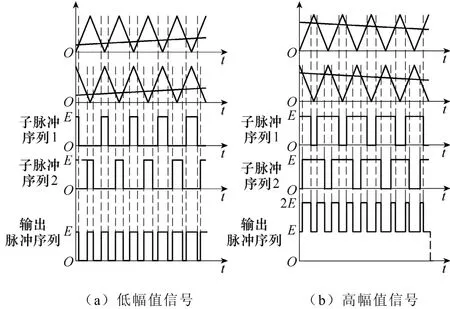
图7 基于载波移相调制的脉冲产生和组合示意图Fig.7 Pulse generation and combination based on phase shifted modulation

3.2 载波移相调制与倍频策略谐波对比分析

3.2.1 自然采样

首先以正弦波自然采样为例。在载波移相调制中，对于图7所示的三角波调制得到的子脉冲序列，在去除直流分量后（若无特别说明，下文均作此处理）其谐波形式的表达式为

式中，m为载波次数（m=0时表示基波）；n为边带谐波的次数。

根据用于分析PWM脉冲序列谐波的二重傅里叶积分理论可以知道，式（9）中等式右边的三部分分别代表信号基波、载波及载波倍数频率的谐波、载波及载波倍数频率谐波的边带谐波。

若采用N条脉冲序列进行组合叠加，每条脉冲序列的载波相位间隔为2π/N，则第i条序列载波所对应的偏移时间为

以ωc(t+toffset(i))替换式（9）中的ωct，即可得出各条序列的谐波表达式，在对其进行组合叠加之后，最终的输出脉冲序列表示为

由于在数学上有

式中，k=1, 2, 3, …，因此o()ft除信号基波以外，仅包含kN次载波谐波及其边带谐波，则式（11）可化简为

以N=4为例（即五电平），取信号频率1kHz，载波频率10kHz，则载波比co/ωω=10，调制比M= 0.9，基于电平组合的载波移相调制策略如图8a所示。可以看到，其第一载波谐波分量位于40kHz，是载波频率的4倍，这正是在脉冲序列组合过程中脉冲频率倍增所带来的效果。

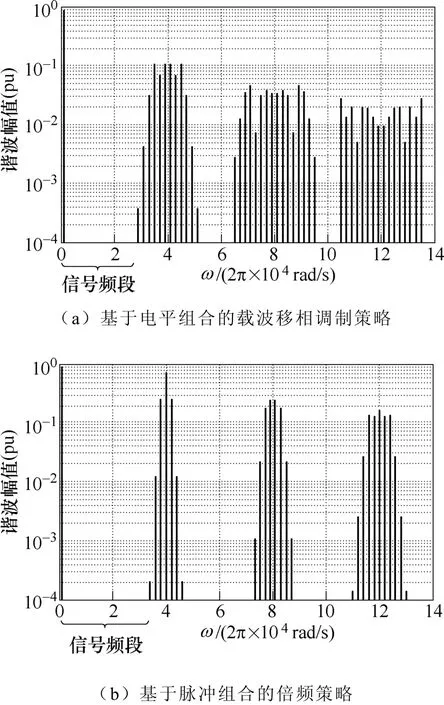
图8 两种典型功率脉冲逻辑组合方法的正弦波自然采样频谱Fig.8 Sinusoidal natural sampling spectrum of two typical power pulse logical combination

另一方面，与其对应的倍频策略频谱可直接由式（9）计算得出，其频谱如图8b所示。其中载波比为40，以保证器件开关频率与上述载波移相调制中开关频率相同。对比二者可以看出，载波移相调制策略中N倍频载波及其倍数次谐波幅值相对较低，但其边带谐波衰减较慢，使得N倍频载波谐波簇整体呈较为“分散”的趋势；而倍频策略中的载波谐波簇则显得较为“集中”，虽然载波谐波本身的幅值相对较高，但其边带衰减得很快。这主要是因为，在相同的子序列脉冲频率fc下，倍频策略的输出脉冲序列的脉宽直接由频率为Nfc的高频载波获取，因此其载波谐波组自然只会出现在kNfc频率处；而载波移相调制则是由频率为fc的载波采样，之后通过各序列移相叠加来进行谐波消除，最终达到将kNfc以外的载波谐波簇完全抵消的效果。而对于kNfc频率处的载波谐波组，虽然无法被完全消除，但也同样受到移相叠加的影响，使得谐波能量更多地扩散到边带当中，从而形成了上述区别。

当然，在载波比足够高的普通变换器中，这一区别并不会造成太大的实质性影响，但对于电力电子功率放大器来说，尤其是在输出频带较宽，输出频率上限较高的情况下，载波比往往被限制在较低的水平，使得载波谐波簇较为接近信号频带范围。此时较为“分散”的载波边带谐波将更容易扩散进入信号频带，从而给输出波形带来额外的谐波失真，或者，从另一个角度来说，压缩了系统的高保真输出频带宽度。因此在电力电子功率放大器中，具有集中式载波频谱的倍频策略将更有利于提高变换器的保真度和输出频带。

3.2.2 规则采样

在当前普遍采用的数字控制系统中，自然采样相对难以实现，因此大都采用规则采样方式。以对称规则采样为例，其频谱和自然采样最大的不同就在于自然采样（特指三角形载波的情况）中可以将奇数次载波的奇次边带谐波以及偶数次载波的偶次边带谐波完全消除，而对称规则采样却无法达到此效果；此外在规则采样中会引入自然采样中不存在的基波边带谐波，从而造成额外的信号波形失真。具体地，正弦波对称规则采样下单条PWM脉冲序列的谐波表达式由式（3）给出，经过类似的推导，可得N条载波移相脉冲序列组合叠加后，最终输出的谐波表达式为

其中

根据式（3）可以给出基于脉冲组合的4倍频策略频谱，两种典型功率脉冲逻辑组合方法的正弦波对称规则采样频谱如图9所示。可以看到，除了与3.2.1节自然采样中类似的载波边带频谱的区别以外，载波移相多电平的基波边带谐波也要明显大于倍频策略。而这些边带谐波通常都位于信号频段之内，这就造成了更为严重的波形失真。

综上所述，基于电平逻辑组合的多电平策略和基于脉冲逻辑组合的倍频策略均可以达到降低谐波含量、提高输出波形保真度、拓宽信号频带等目的。但针对电力电子功率放大器，仅从基本的脉冲组合角度来分析，倍频策略在相同的器件开关频率下可以提供更宽的信号频带以及更小的信号边带谐波，并且其性能受信号幅值，即调制比的影响较小，因此要优于多电平策略。当然，多电平策略由于具有减小单个器件耐压，减小输出状态切换时的du/dt等特点，因此在其他应用场合，尤其是大功率领域仍具有额外优势，在相关应用中需要进行权衡考虑。

4 结论

本文从电力电子系统中最底层的功率脉冲组合理论出发，首先阐述了功率脉冲纯时序组合的概念和局限性，由此引出功率脉冲逻辑组合的概念，并提炼出基于电平、脉冲以及边沿的三种功率脉冲逻辑组合方式。

在此基础上，一方面对多重化、多电平等现有技术中的脉冲组合思想进行了总结归纳；另一方面提出了基于脉冲序列逻辑组合的倍频策略。该策略的特征在于，通过多条脉冲序列的逻辑组合，使得变换器输出脉冲频率为器件实际开关频率的若干倍，从而达到突破现有器件开关频率限制的效果。

由于现有的多电平策略以及上述倍频策略均可以在不同方面提升变换器的性能，本文以电力电子功率放大器的应用需求为例，对两种策略的脉冲频谱特征进行了深入对比分析，从而明确了两种方法的适用性，同时以此为例，展示了基于功率脉冲组合理论的分析思路和应用价值。

[1] 白华. 电力电子变换器中电磁脉冲功率瞬态过程研究[D]. 北京： 清华大学, 2007.

[2] 王立乔, 严江涛. 基于目标波形与逻辑组合的多电平变流器通用调制算法设计[J]. 电力系统自动化, 2013, 37(12)： 87-91. Wang Liqiao, Yan Jiangtao. Design of general modulation algorithm of multilevel converter based on target waveform and logic combination[J]. Automation of Electric Power Systems, 2013, 37(12)：87-91.

[3] Yu S H, Tseng M H. Optimal control of a nine-level class-D audio amplifier using sliding-mode quantization[J]. IEEE Transactions on Industrial Electronics, 2011, 58(7)： 3069-3076.

[4] Zhang Y, Cai L, Meng Q D, et al. A high-efficiency cascade multilevel class-D amplifier with sliding mode control[C]//IEEE Conference on Robotics, Automation and Mechatronics, Chengdu, 2008： 1212-1216. [5] Ertl H, Kolar J W, Zach F C. Analysis of a multilevel multicell switch-mode power amplifier employing the "flying-battery" concept[J]. IEEE Transactions on Industrial Electronics, 2002, 49(4)： 816-823.

[6] 汪世平. 倍频式IGBT高频感应加热电源的研究[D].杭州： 浙江大学, 2005.

[7] Grahame H D, Lipo Thomas A. 电力电子变换器PWM技术原理与实践[M]. 北京： 人民邮电出版社, 2010.

[8] Rodríguez J, Lai J S, Fang Z P. Multilevel inverters：a survey of topologies, controls, and applications[J]. IEEE Transactions on Industrial Electronics, 2002, 49(4)： 724-738.

[9] Cho I H, Cho K M, Kim J W, et al. A new phase-shifted full-bridge converter with maximum duty operation for server power system[J]. IEEE Transactions on Power Electronics, 2011, 26(12)：3491-3500.

[10] 王铁军, 饶翔, 姜小弋, 等. 用于多重化逆变的移相变压器[J]. 电工技术学报, 2012, 27(6)： 32-37. Wang Tiejun, Rao Xiang, Jiang Xiaoyi, et al. A phase-shift transformer applied in multi-module inverters[J]. Transactions of China Electrotechnical Society, 2012, 27(6)： 32-37.

[11] 文小玲, 尹项根. 大容量多重化逆变器的输出电压谐波分析[J]. 高电压技术, 2007, 33(10)： 191-196. Wen Xiaoling, Yin Xianggen. Voltage harmonic analysis of the multi-pulse inverter with large capacity[J]. High Voltage Engineering, 2007, 33(10)：191-196.

[12] Floriani J C A. Generalized analysis of current ripple in a pulsewidth modulation H-bridge converter with unipolar-bipolar switching[J]. IEEE Power Electronics Letters, 2004, 2(3)： 83-86.

[13] Agelidis V G, Calais M. Application specific harmonic performance evaluation of multicarrier PWM techniques[C]//29th Annual IEEE Power Electronics Specialists Conference, Fukuoka, Japan, 1998： 172-178.

（编辑 陈 诚）

Power Pulse Sequential Combination and Logical Combination in Power Electronics

Chen Kainan Zhao Zhengming Yuan Liqiang
（State Key Lab of Control and Simulation Power System and Generation Equipment Department of Electrical Engineering Tsinghua University Beijing 100084 China）

This paper focuses on the basic theories of pulse combination in power electronics. The concept, method and realization of power pulse sequential combination and logical combination are summarized and analyzed. Aiming at the limitations of power pulse sequential combination, the power pulse (sequence) logical combination, as well as the methods and applications, is introduced. Both typical methods based on different pulse logical combination ideas, i.e. multilevel technology and frequency multiplication strategy, are effective in improving the performances of system. Thus, taken the power electronics amplifier as an analysis object, their harmonic characteristics and applicability are compared and contrasted. With the study of pulse combination methodology in power electronics, the relative technologies can be systematically understood, moreover, novel pulse combination and realization methods can be expanded. It is helpful to promote the development of power electronics.

Pulse sequential combination, pulse logical combination, frequency multiplication strategy, harmonic analysis

TM46

陈凯楠 男，1988年生，博士，助理研究员，主要研究方向为无线电能传输、电力电子功率放大技术等。

E-mail： chenkn@tsinghua.edu.cn（通信作者）

赵争鸣 男，1959年生，教授，博士生导师，主要研究方向为大容量电力电子变换系统、光伏发电、电机控制和无线电能传输等。E-mail： zhaozm@tsinghua.edu.cn

10.19595/j.cnki.1000-6753.tces.170589

国家自然科学基金重大项目资助（51490680，51490683）。

2017-04-08 改稿日期 2017-05-18