风力机组尾迹控制策略研究

王渊博， 李 春,2， 缪维跑， 丁勤卫， 郝文星

(1.上海理工大学 能源与动力工程学院，上海 200093；2.上海市动力工程多相流与传热重点实验室，上海 200093)



风力机组尾迹控制策略研究

王渊博1， 李 春1,2， 缪维跑1， 丁勤卫1， 郝文星1

(1.上海理工大学 能源与动力工程学院，上海 200093；2.上海市动力工程多相流与传热重点实验室，上海 200093)

为减小风力机尾迹的影响，以实现风场总功率最大化及风力机组气动性能全局协调控制的目标，采用大涡模拟(Large Eddy Simulation, LES)方法，基于致动线模型，利用开源CFD软件OpenFOAM对9种风力机组偏航控制及9种风场错列布置进行数值模拟，比较这18种方案的风场总功率，并结合流场参数分析不同尾迹控制策略影响风场下游风力机的流动机理.结果表明：尾迹对下游风力机气动性能影响严重；2种尾迹控制方法均可实现全风场优化，其中各偏航控制下，风场总功率最大可提高35.3%，风场错列布置时最大可提高68.5%.

风力机组； 尾迹； 偏航； 错列； OpenFOAM； 致动线模型

风力发电是目前可再生能源利用中技术最成熟、开发应用规模最大和商业化程度最高的发电方式[1].为获取更多风能，商业化的风力机均“集中”运行于某一风场中[2]，上游风力机汲取风能的同时会对风场原有流动产生影响[3]，造成下游风力机常处于上游风力机尾迹中，尾迹区的速度亏损和高湍流度将导致下游风力机输出功率显著降低，浪费了风能和土地资源，提高了风电成本.因此，研究尾迹控制策略，提高风场总功率以降低风能成本(Cost of Wind Energy,COWE)成为当前风电研究的热点方向之一[4].

2015年，Hornung等[5]利用OpenFOAM研究了上游风力机尾迹的结构特点及其对下游风力机性能的影响，得出风力机尾迹区速度减小和湍流强度增加会严重减弱下游风力机气动性能的结论，但Hornung等未能从风场总功率的角度考虑尾迹的影响.同年，Gebraad等[6]通过高精度风场仿真专用软件SOWFA(Simulator for Wind Farm Applications)以调整桨距角和扭矩的方法进行数值计算，但结果表明该方法对于提高风场总功率效果不佳.2014年，Fleming等[7]基于大涡模拟(LES)方法，通过独立变桨控制(Individual Pitch Control,IPC)以减小尾迹速度亏损效应，结果显示风场总功率提高有限且叶根弯矩成倍增加.张昇龙[8]基于Fluent软件对某商用1.5 MW风力机在3种不同来流风况下的尾迹和气动性能进行模拟，并将计算结果与相似实验的结果进行对比，验证了三维黏性不可压缩模型的准确性，但文中仅对单台1.5 MW风力机进行了CFD数值计算.因为CFD方法需要大量近壁面网格以分辨边界层流动，数值模拟多台兆瓦级风力机时计算量巨大，时间与成本难以承受，所以此方法用于工程设计并不现实.贾彦等[9]利用WAsP风场微观选址软件及风资源数据进行风力机组风场模拟，比较不同风力机组布局下的风场年净发电量，给出了最优风力机组布局，但WAsP软件的计算结果与真实风场存在较大误差，无法获得风力机周围流场的详细信息[10].2016年，Shives等[11]基于致动盘模型，以全风场总功率为目标进行风场布置优化，给出了最佳风场布置，但与致动线基于叶片对风轮进行简化不同，致动盘模型将风轮简化成对称圆盘，导致风轮无法旋转，因而计算结果相比致动线模型较为粗糙[12].李少华等[13]采用雷诺时均(Reynolds-Averaged Navier-Stokes,RANS)方法，结合尾流理论分别对单机、2台串列及错列布置的风力机进行数值模拟，结果表明错列布置比串列布置受尾迹的影响小，但由于采用RANS方法，过多的流动细节被平均，无法获取流场的细微结构.

为此，笔者以美国国家可再生能源实验室(National Renewable Energy Laboratory,NREL)设计的5 MW风力机为研究对象，基于致动线模型，采用LES方法，利用开源CFD软件OpenFOAM对多种风力机组偏航控制和风场错列布置方案进行数值计算，比较各工况下的风场总功率，并结合流动参数分析尾迹影响下游风力机的流动机理，为减小COWE、风电场运行及微观选址提供参考.

1 致动线模型

1.1 控制方程

致动线模型控制方程的矢量形式为：

(1)

式中：V为速度矢量；t为时间；ρ为流体密度；p为压强；ν为运动黏度；源项f为体积力，表征叶片对流场的反作用力，传统CFD方法模拟风场时的控制方程忽略这一项.

1.2 体积力

作用力与反作用力是任何物体受力的一般表现[14]，即流体作用于叶片的力与叶片作用于流体的力大小相等，因此可利用流体对叶片的作用力求得叶片对流体的体积力.叶片所受作用力计算如下：

(2)

(3)

(4)

式中：W为当地翼型的相对速度；c为当地翼型弦长；Cτ为切向力系数；τ为切向单位向量；Cn为法向力系数；n为法向单位向量；Fτ、Fn和Fs分别为当地翼展单位长度所受到的切向力、法向力及合力.

当地翼展单位长度叶片对流场的体积力Ff为：

(5)

叶片对流场的体积力需投射至致动线附近的计算区域，称为体积力光顺，如图1所示.

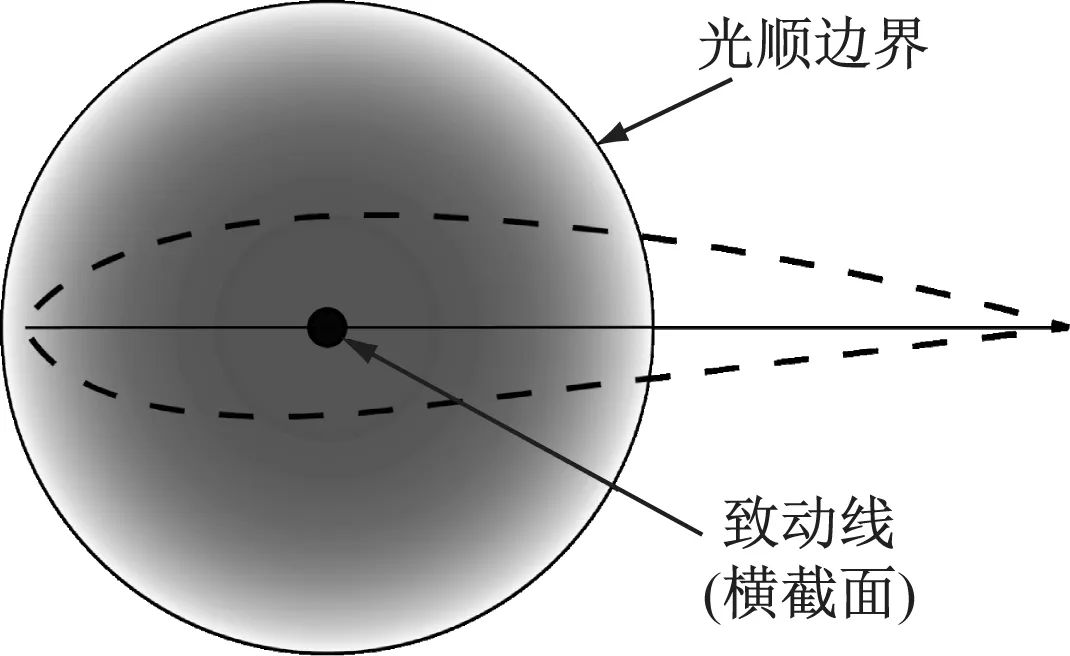
图1 体积力光顺示意图Fig.1 Distribution of body force

体积力的光顺一般采用三维高斯分布的方式，如式(6)所示，大量研究表明此分布方式与真实情况最相符[15].此外，为提高计算效率，同时兼顾精确度，需确定体积力光顺边界，边界上投射的体积力大小为最大体积力的5%，边界之外不再进行体积力光顺[16].

(6)

式中：r为体积力中心至投射点的距离；ε为分布因子，控制体积力分布的集中程度.

分布因子过小时，体积力投射范围较小，数值计算将产生严重震荡，甚至无法收敛；分布因子较大时，体积力投射范围过大，投射区域网格所得体积力过小，流场状态改变微弱，尤其是叶尖涡和叶根涡被过分抹平，与真实情况不符[17].

1.3 致动线求解器

pisoFoam是OpenFOAM的标准求解器，基于解耦N-S方程的瞬态压力全隐分离式(PISO)算法，可求解湍流及层流流动，相比压力耦合方程半隐式(SIMPLE)算法，该算法计算效率及精度更高[18].基于pisoFoam求解器构造新求解器pisoFoamTurbine，专用于致动线方法对风力机的数值模拟.与pisoFoam相比，pisoFoamTurbine通过建立C++类“turbines”，实现了定义体积力数组、求解体积力大小和光顺体积力等一系列操作.

pisoFoamTurbine中动量方程的代码变为：

fvVectorMatrix UEqn

(

fvm::ddt(U)

+ fvm::div(phi, U)

+ turbulence->divDevReff(U)

- turbines.force()

);

2 计算模型与网格

2.1 风场布置

计算模型选用NREL设计的5 MW风力机，该风力机额定风速为11.4 m/s，额定转速为12.1 r/min，风轮直径为126.0 m，轮毂直径为3.0 m，风轮锥角为2.5°，轮毂高度为90.0 m.以风轮直径D为基准，模拟偏航控制的风场尺度为20D×6D×6D，模拟风场错列的风场尺度为20D×8D×6D.在模拟风场中串列布置2台NREL 5 MW风力机，分别为WT1和WT2，如图2所示.其中，WT1距入口为3D，WT2距WT1为7D，出口距WT2为10D.图2中x轴正方向为风的流动方向，z轴正方向为风场高度方向.

2.2 尾迹偏移控制策略

第一，内部控制能够完善企业治理结构。企业的改革需要完善企业内部制度，现代企业的发展需要完善的制度支撑，公司管理制度和法人治理结构是现代企业制度的重要框架，产权明晰、责权利明确等，完善的内部控制制度促进企业的决策支持系统、管理系统和监督系统高效的运转，内部控制制度是企业治理结构的重要组成部分。

2.2.1 偏航控制

控制风场上游风力机WT1进行偏航，使其尾迹偏离下游风力机WT2风轮的中心位置.共模拟9种偏航工况，偏航角取值为230°～310°，步长为10°.图3为WT1偏航示意图，其中y轴正方向为风场横向方向.

图2 风场布置Fig.2 Layout of the wind farm

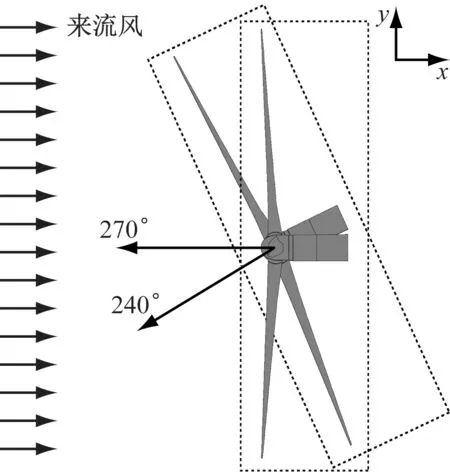
图3 WT1偏航示意图Fig.3 Yaw arrangement of WT1

2.2.2 风场错列

错列布置风力机组以使下游风力机WT2部分或完全移出上游风力机WT1的尾迹.共对9种错列布置方案进行数值模拟，WT2分别向y轴正负方向移动0.5D、0.75D、1.0D和1.25D.图4为风场错列布置示意图.

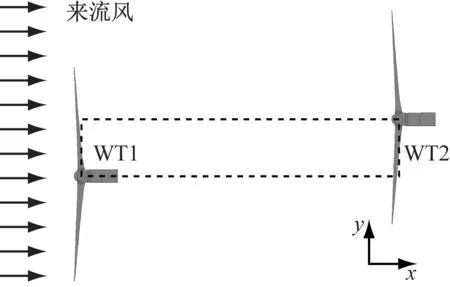
图4 风场错列布置示意图Fig.4 Staggered arrangement of wind turbines

2.3 网格与边界条件

致动线方法的优势在于无需对风力机建模，可将风场计算域全部处理为正交网格，极大地提高了计算精度和速度[12].对计算域中风轮所在水平区域的网格进行加密，并在网格加密区与粗网格区之间添加2层网格过渡带,以避免数值计算震荡.计算域网格划分如图5所示，网格精度从外向内依次加倍，其中加密区网格精度为3.94 m×3.94 m×3.94 m，与Fleming等[7]模拟风场时的网格尺度相近.此外，2种控制策略所用的计算域边界条件设置相同，进口为速度入口，速度方向平行于x轴，大小为该风力机的额定风速11.4 m/s；出口为压力出口，压力大小为一个标准大气压；下界面及上界面为滑移边界条件；2个侧面为周期性边界条件.

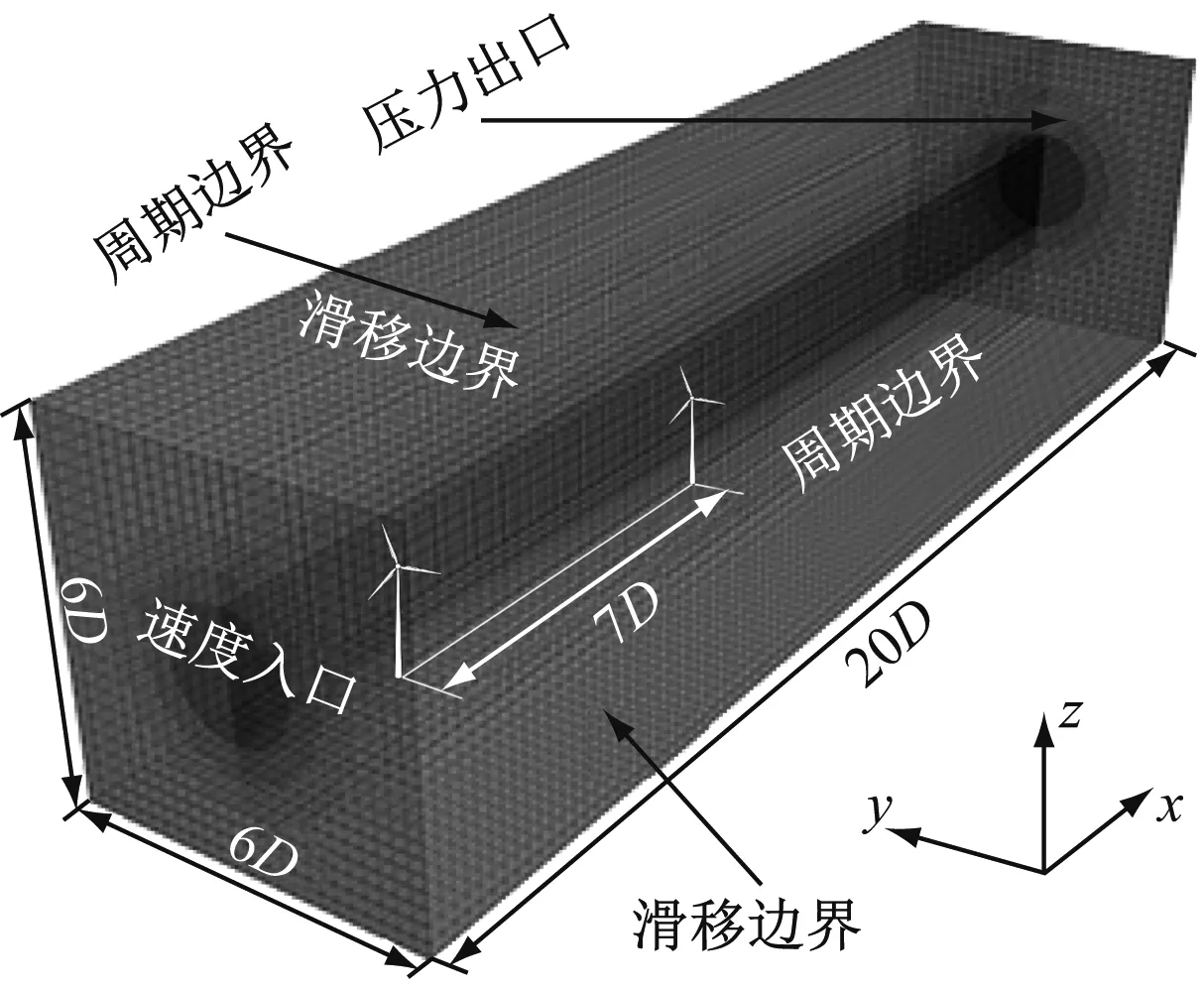
(a) 偏航控制

(b) 风场错列图5 计算域网格划分Fig.5 Mesh generation of the calculation domain

采用LES方法，流动变量通过网格过滤操作分为网格尺度(Grid Scale,GS)和亚格子尺度(Sub Grid Scale,SGS)2部分，引入各向异性的残余应力张量模型封闭亚格子模型.利用Smagorinsky涡黏假设参数化，将模型分为2部分：线性涡黏模型和基于混合长假设的亚尺度涡黏模型[19].

3 结果与分析

pisoFoamTurbine求解器在每个时间步输出风力机组的功率.图6为偏航控制与风场错列布置下各风力机的输出功率.

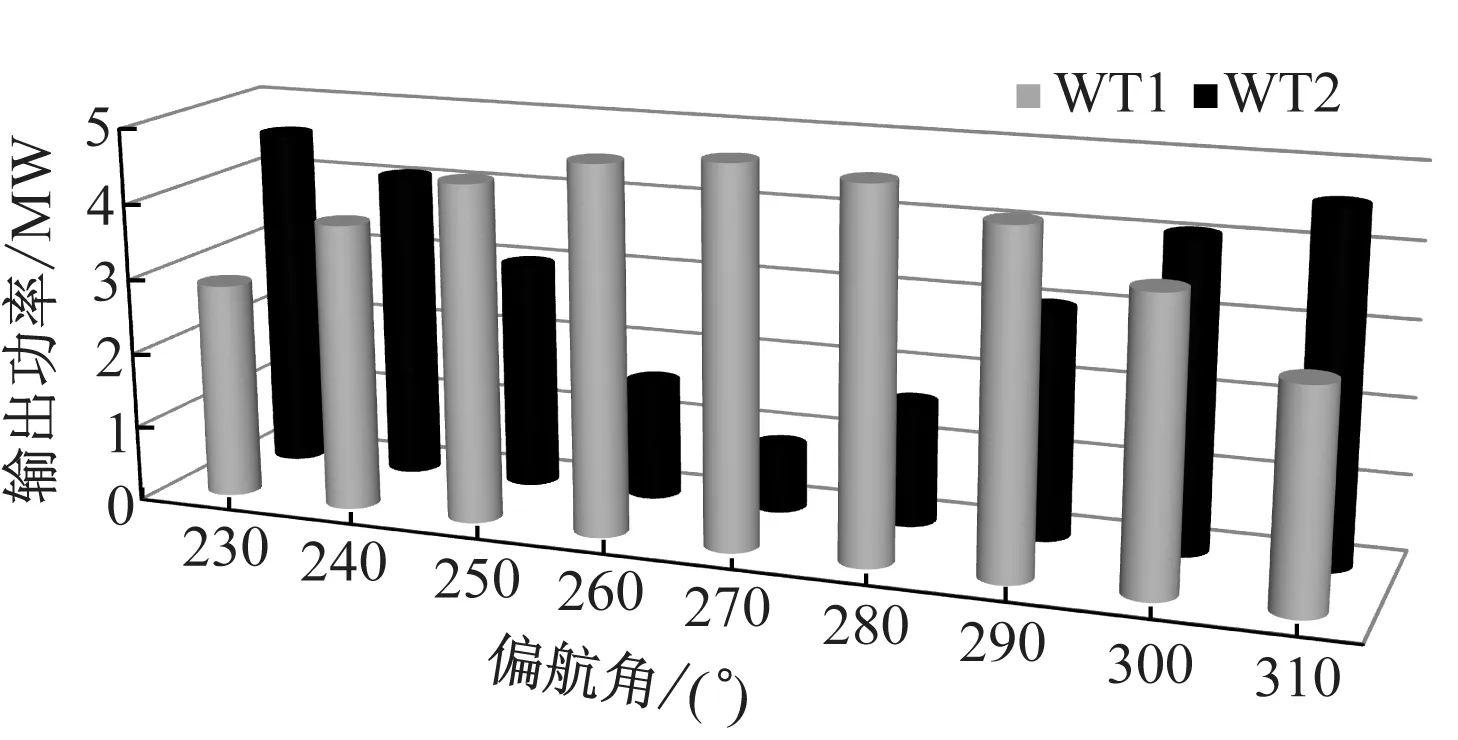
(a) 偏航控制

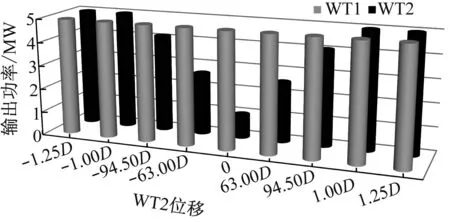
(b) 风场错列图6 各风力机的输出功率Fig.6 Power output of wind turbines

从图6(b)风场错列布置时风力机输出功率可以看出，WT2向y轴正方向移动时，风力机输出功率逐渐增大，当移动1.0D时，WT2的输出功率为5.041 8 MW，当移动1.25D时，WT2的输出功率为5.062 4 MW，可见移动1.0D时风力机输出功率并没有移动1.25D时大，说明移动1.0D时WT1的尾迹仍对WT2有影响.WT2向y轴负方向移动的过程中，其输出功率变化趋势与WT2向y轴正方向移动时相同，但移动-0.5D、-0.75D和-1.0D时，WT2的输出功率比对应y轴正方向时稍大.从图6(b)还可以看出，上游WT1的输出功率变化不大，这是因为入流风速始终无变化；随WT2移动距离的增大，WT1输出功率稍有增大，证明下游风力机WT2对上游风力机WT1也有一定影响.此外，以移动0为基点，WT2的输出功率几乎呈对称关系，这一方面说明随着下游风力机在y轴移动距离的增大，其受上游风力机影响越小，另一方面也进一步证明了计算结果的准确性和所用方法的可行性.

图7为偏航控制和风场错列布置下的风场总功率曲线图，用以对比2种不同尾迹控制策略对风场总功率的影响.从图7可直观地看出，风场错列布置下的风场总功率整体高于偏航工况下.

图7 风场总功率Fig.7 Total power output of the wind farm

选用三次多项式为基函数，利用最小二乘法分别拟合偏航和风场错列2种控制方法下风场总功率随偏航角与WT2位移的关系，可得式(7)和式(8)所示关系式.

P1=-3.072 4θ3+0.000 8θ2+

0.427θ+63.956 3

(7)

P2=0.052 7l3+2.273 8l2-

0.073 7l+7.084 5

(8)

式中：P1为偏航控制策略时的风场总功率，MW；θ为偏航角，变化范围为230°～310°；P2为风场错列布置时的风场总功率，MW；l表示WT2的位移.

图8(a)和图8(b)分别为无错列布置时距WT2为3D和6D处的压力云图与速度云图.从图8(a)可知，尾迹沿轴向距WT2越远，压力恢复越完全.从图8(b)可以看出，尾迹沿轴向距WT2越远，速度亏损也越小.压力与速度沿轴向的变化趋势与理论分析完全吻合.

图9为偏航控制下风力机轮毂高度处的速度云图.从图9可知，偏航控制可有效改变WT1的尾迹流向，偏航角越大，WT1尾迹偏离WT2风轮中心幅度越大，且尾迹偏移以270°偏航角为基准呈对称分布，与图6结果相符.上游风力机无偏航时，WT1的尾迹全部落在WT2的风轮上，造成WT2完全运行在WT1的尾迹中，输出功率仅为0.857 9 MW，只有此时WT1输出功率的17.2%.WT1偏航角为250°和290°时，WT2风轮约有一半运行在WT1的尾迹中，WT2的输出功率分别为3.021 2 MW和3.018 2 MW，已经超过无偏航控制策略时WT2输出功率的2倍，输出功率提升显著.当WT1偏航角为230°时，WT2输出功率为4.576 5 MW，已非常接近其额定功率，但由于此时WT1严重偏离设计工况，输出功率已经非常低，导致风场总功率并非最高.

(a) 压力云图

(b) 速度云图图8 无错列时尾迹横截面云图Fig.8 Clouds of wake cross-section in normal arrangement

图9 偏航控制策略时速度云图Fig.9 Velocity clouds in yaw arrangement of wind turbines

图10为风场错列布置时流场的涡量图.叶片阻力面的压力高，升力面的压力低，压差推动气流绕过叶尖，形成叶尖涡，风力机的叶尖涡在来流风速叠加下，不易从迹线或速度矢量上直接显示出漩涡位置，因而引入涡量以显示涡.只有当工质平稳顺滑地流过风力机叶片翼型时才能产生最大升力，涡量太大会造成风力机叶片翼型性能偏离设计工况，因而风轮在受尾迹涡影响较小的情况下输出功率较高.从图10可以看出，WT2沿y轴方向没有移动时，完全运行在上游风力机WT1的尾迹涡中，导致输出功率极低，随着WT2向y轴正负方向移动，其受WT1尾迹涡的影响越来越弱，因而输出功率越来越高，尤其是移动距离为1.25D时完全不受WT1尾迹涡的影响，输出功率最大，此与图6所示结果一致.此外，WT1尾迹逆时针旋转造成其向y轴正方向偏转，最终导致WT2在y轴正方向比y轴负方向输出功率小.

图10 风场错列布置涡量图

Fig.10 Wind farm vorticity in staggered arrangement of wind turbines

4 结 论

(1) 风场上游风力机尾迹对下游风力机气动性能产生严重影响，大幅降低其输出功率，但通过尾迹控制策略可减弱上游风力机尾迹的影响.

(2) 偏航控制策略可使风场上游风力机尾迹偏移下游风力机风轮中心，虽上游风力机输出功率有所降低，但下游风力机输出功率大幅提升，从而风场总功率得以升高.

(3) 风场下游风力机横向移动造成风场错列，可避免下游风力机完全运行在上游风力机尾迹中，使上游风力机在输出功率几乎不变的情况下显著提高风场总功率.

[1] 丁勤卫, 李春, 周国龙, 等. 陆海风力机动态响应对比[J]. 动力工程学报, 2016, 36(1): 65-73.

DING Qinwei, LI Chun, ZHOU Guolong, et al. Comparison of dynamic response between stationary and floating wind turbines[J]. Journal of Chinese Society of Power Engineering, 2016, 36(1): 65-73.

[2] 李少华, 匡青峰, 吴殿文, 等. 1.2 MW风力机整机流场的数值模拟[J]. 动力工程学报, 2011, 31(7): 551-556.

LI Shaohua, KUANG Qingfeng, WU Dianwen, et al. Numerical simulation on flow field of a 1.2 MW wind turbine[J]. Journal of Chinese Society of Power Engineering, 2011, 31(7): 551-556.

[3] KECSKEMETY K M, MCNAMARA J J. Influence of wake dynamics on the performance and aeroelasticity of wind turbines[J]. Renewable Energy, 2016, 88: 333-345.

[4] GAO Xiaoxia, YANG Hongxing, LU Lin. Optimization of wind turbine layout position in a wind farm using a newly-developed two-dimensional wake model[J]. Applied Energy, 2016, 174: 192-200.

[5] HORNUNG C, VIELLIEBER M, CLASS A. Simulation of wake effects of wind farms using an actuator disk implementation[J]. PAMM, 2015, 15(1): 487-488.

[6] GEBRAAD P M O, FLEMING P A, van WINGERDEN J W. Comparison of actuation methods for wake control in wind plants[C]∥Proceedings of American Control Conference. Chicago, IL: IEEE, 2015: 1695-1701.

[7] FLEMING P A, GEBRAAD P M O, LEE S, et al. Evaluating techniques for redirecting turbine wakes using SOWFA[J]. Renewable Energy, 2014, 70: 211-218.

[8] 张昇龙. 水平轴风力机尾流场及其气动性能的研究[D]. 兰州: 兰州理工大学, 2014.

[9] 贾彦, 刘璇, 李华, 等. 考虑尾流效应对风电场机组布局的影响分析[J]. 可再生能源, 2014, 32(4): 429-435.

JIA Yan, LIU Xuan, LI Hua, et al. Analysis of wind farm units layout considering wake effect[J]. Renewable Energy Resources, 2014, 32(4): 429-435.

[10] PINARD J P. Computer models for wind flow over mesoscale mountainous terrain applied to the Yukon[R]. Edmonton: International Conference on Engineering and Simulation, 1999: 1-45.

[11] SHIVES M, CRAWFORD C. Adapted two-equation turbulence closures for actuator disk RANS simulations of wind & tidal turbine wakes[J]. Renewable Energy, 2016, 92: 273-292.

[12] 王强. 水平轴风力机三维空气动力学计算模型研究[D]. 北京: 中国科学院研究生院(工程热物理研究所), 2014.

[13] 李少华, 岳巍澎, 匡青峰, 等. 双机组风力机尾流互扰及阵列的数值模拟[J]. 中国电机工程学报, 2011, 31(5): 101-107.

LI Shaohua, YUE Weipeng, KUANG Qingfeng, et al. Numerical simulation of wake interaction and array of double wind turbine[J]. Proceedings of the CSEE, 2011, 31(5): 101-107.

[14] 张晓春, 刘迈, 李晶. 大学物理全程导学[M]. 北京: 中国电力出版社, 2010.

[15] SØRENSEN J N, SHEN W Z. Numerical modeling of wind turbine wakes[J]. Journal of Fluids Engineering, 2002, 124(2): 393-399.

[16] JIN Wenjie. Numerical simulation of wind turbine wakes based on actuator line method in NEK5000[D]. Stockholm: Royal Institute of Techno-logy, 2013.

[17] 刘磊. 风力机叶片非定常气动特性的研究[D]. 北京: 中国科学院研究生院(工程热物理研究所), 2012.

[18] 李东岳. OpenFOAM中植入的PISOSIMPLE算法详解[EB/OL]. (2016-03-12) [2016-05-10]. http://www.doc88.com/p-2486927873190.html.

[19] 卞凤娇, 徐宇, 王强, 等. 基于OpenFOAM的风力机致动线模型研究[J]. 工程热物理学报, 2016, 37(1): 72-75.

BIAN Fengjiao, XU Yu, WANG Qiang, et al. Numerical study of actuator line model of wind turbine based on OpenFOAM platform[J]. Journal of Engineering Thermophysics, 2016, 37(1): 72-75.

Study on Control Strategies for Wind Turbine Wakes

WANGYuanbo1,LIChun1,2,MIAOWeipao1,DINGQinwei1,HAOWenxing1

(1. School of Energy and Power Engineering, University of Shanghai for Science and Technology,Shanghai 200093, China; 2. Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, Shanghai 200093, China)

To reduce the adverse effects of wind turbine wakes, and to effectively maximize the total power output and coordinately control the aerodynamic performance of wind turbines, numerical simulations were conducted on the control strategies by 9 yaw and 9 staggered arrangements of wind turbines using OpenFOAM based on ALM and LES, so as to compare the total power output of the wind farm among above 18 wake control strageties, while the influencing mechanism of different wake control strategies on the downstream wind turbine flow was analyzed with the help of fluid field parameters. Results show that the wake severely affects the aerodynamic performance of the downstream wind turbine; both the wake control modes could optimize the global wind farm, and among all the yaw arrangements, the total power output could be impoved by a maximum of 35.3%, and among all the staggered arrangements, it could be improved by a maximum of 68.5%.

wind turbine; wake; yaw arrangement; staggered arrangement; OpenFOAM; ALM

2016-07-20

2016-08-25

国家自然科学基金资助项目(51176129，51676131)；上海市科学技术委员会资助项目(13DZ2260900)

王渊博(1991-)，男，陕西澄城人，硕士研究生，研究方向为风电场. 李 春(通信作者)，男，教授，博导，电话(Tel.)：15216702797；E-mail：lichun_usst@163.com.

1674-7607(2017)07-0584-06

TK83

A

480.60