火电厂主蒸汽温度UMDA整定模糊PID控制算法

王天堃

(神华集团有限责任公司， 北京 100011)



火电厂主蒸汽温度UMDA整定模糊PID控制算法

王天堃

(神华集团有限责任公司， 北京 100011)

针对火电厂锅炉主蒸汽对象的温度控制变参数、大时滞问题，提出了一种基于单变量分布估计优化算法(UMDA)整定的模糊PID控制算法，以改善温度控制效果.对于给出的大时滞系统模型，首先在PID控制器的基础上通过模糊控制规则并行地进行辅助修正，采用UMDA对其中参数进行整定，实现对模糊PID的自整定优化设置，最后对所设计的时滞温控系统进行仿真分析.结果表明:采用所提方法系统在无扰情况下基本不存在超调，摄动输入下也能明显地降低超调量，且调整时间较短，明显改善了原系统的动态性能和静态性能.

温度控制； 模糊PID； UMDA

锅炉蒸汽温度的控制品质对火力发电机组的安全经济指标有着重要影响，是考核火电厂热工控制系统控制水平和机组运行质量的首选评价指标[1].一般来说，大型火电机组蒸汽温度的变负荷动态偏差要求控制在设定值±8 K以内，稳定负荷静态偏差要求控制在±3 K以内，这对火电厂机组主蒸汽温度控制系统的要求较高.而该控制系统的本质是利用一个反应特性较慢的减温水扰动来克服反应特性较快的过热器吸热量扰动[2]，被控对象体现出明显的大时滞特性，且兼有随机组负荷变化而变化的对象模型参数摄动特性，使得火电厂过热蒸汽温度通常难以达到很好的控制品质.

近年来，新的智能比例积分微分(PID)控制算法开始在火电厂蒸汽温度(以下简称汽温)控制中得到重视，陆续出现了汽温的自适应递阶模糊PID控制[3]、串级模糊PI的控制系统[4]、多种机组汽温控制策略[5]和模糊推理的模糊PID[6]等应用研究.

一般情况下，这些智能控制算法计算量大、控制规律复杂，很难满足实时性要求[7-8].所以，除了利用专家系统结合PID控制器改善锅炉稳定性的方法外[9-10]，还可采用遗传算法、粒子群算法改善模糊PID控制器的控制效果[11-12]，以及直接使用改进遗传算法整定PID控制器的算法[13]等.而单变量分布估计优化算法(UMDA)可以避免传统遗传算法中交叉算子和变异算子带来的盲目性，能有效提高搜索效率[14]，从而加快控制算法的参数寻优速度.

笔者结合某300 MW燃煤火电机组锅炉汽温控制对象的特点，基于传统的PID控制算法，设计了一种单变量分布估计优化封装的自整定模糊PID控制算法.该算法能够利用自定义的模糊规则对传统PID的控制效果和控制性能进行优化，并采用单变量分布估计优化算法进行参数的快速自适应调整.

1 火电厂主蒸汽温度模型

根据某300 MW燃煤火电机组的动态特性构建被控模型，其系统框架见图1.由于采用双冲量汽温控制方式，被控对象分为喷水减温器前的导前区部分和喷水减温器后的惰性区部分.一般情况下，由导前区汽温对象作为被调量构成一个内回路，该内回路的动态特性较快，大多数为低阶或单阶的小时间常数惯性对象；同时由惰性区汽温对象作为被调量组成一个外回路，外回路的动态特性则为大时间常数的高级惯性对象.系统模型如下：

(1)

该模型的导前区特性G1为一单阶对象特性，而惰性区特性G2为一四阶等容惯性环节特性，U为控制量，Y为系统输出.对于大多数300 MW以上的采用三段式喷水减温的燃煤火电机组来说，这种假设不影响随后推导出的各种汽温控制策略的普遍适用价值.

2 基于UMDA优化的模糊PID

图1中的主蒸汽温度控制器采用经典负反馈PID控制和基于专家知识的模糊控制相互补充，其框架如图2所示.控制系统以数字PID控制模块为基础，加入模糊控制器进行辅助修正，并采用单变量分布估计优化算法对控制器参数进行优化，从而实现系统的各参数自动整定与优化整定，这一方面是为了解决传统控制方法中调整时间与超调量的冲突问题，取得更好的控制效果；另一方面，由于控制系统参数能自适应整定，将更方便用户使用.

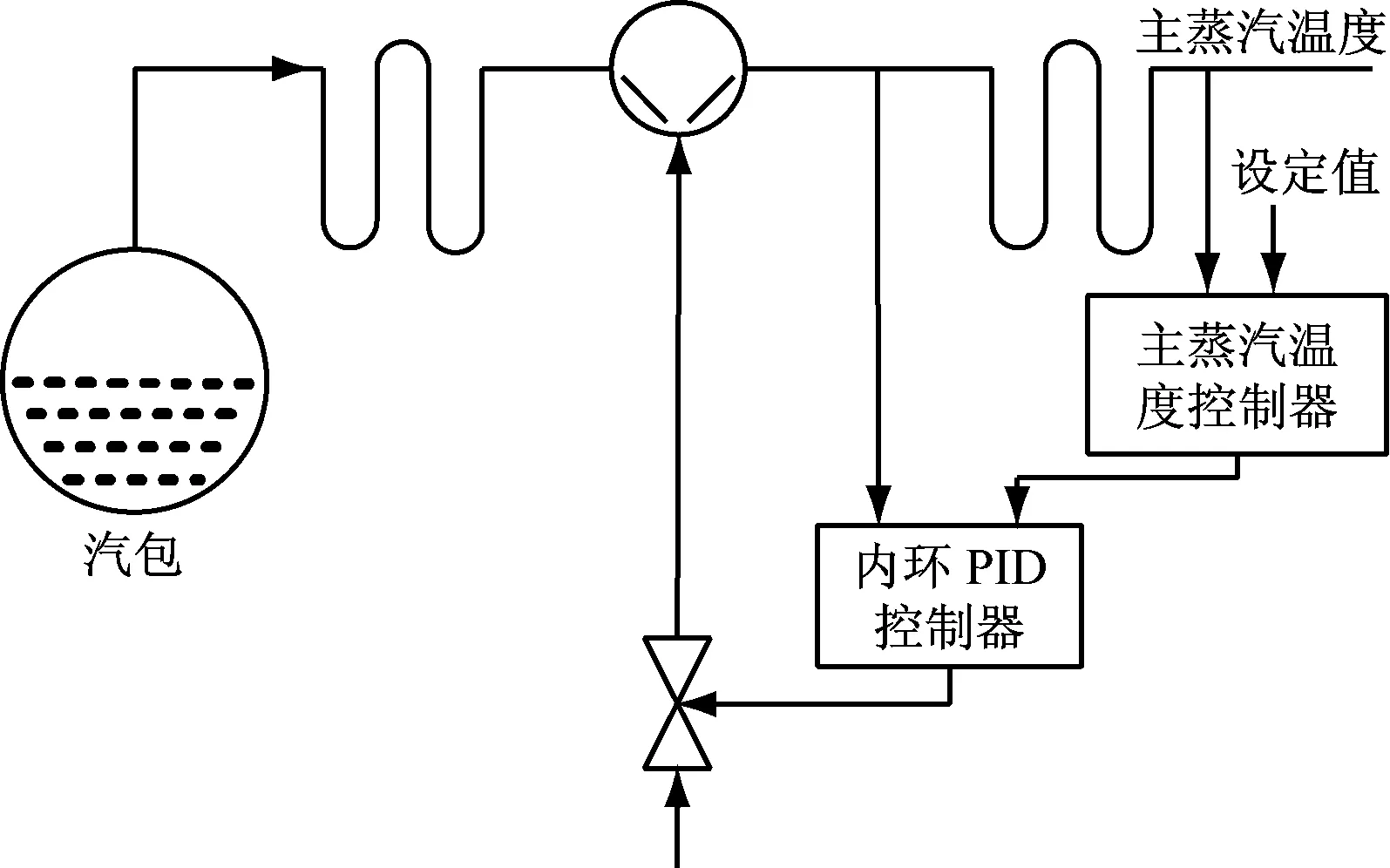
图1 系统整体框架示意图Fig.1 Schematic diagram of the overall system

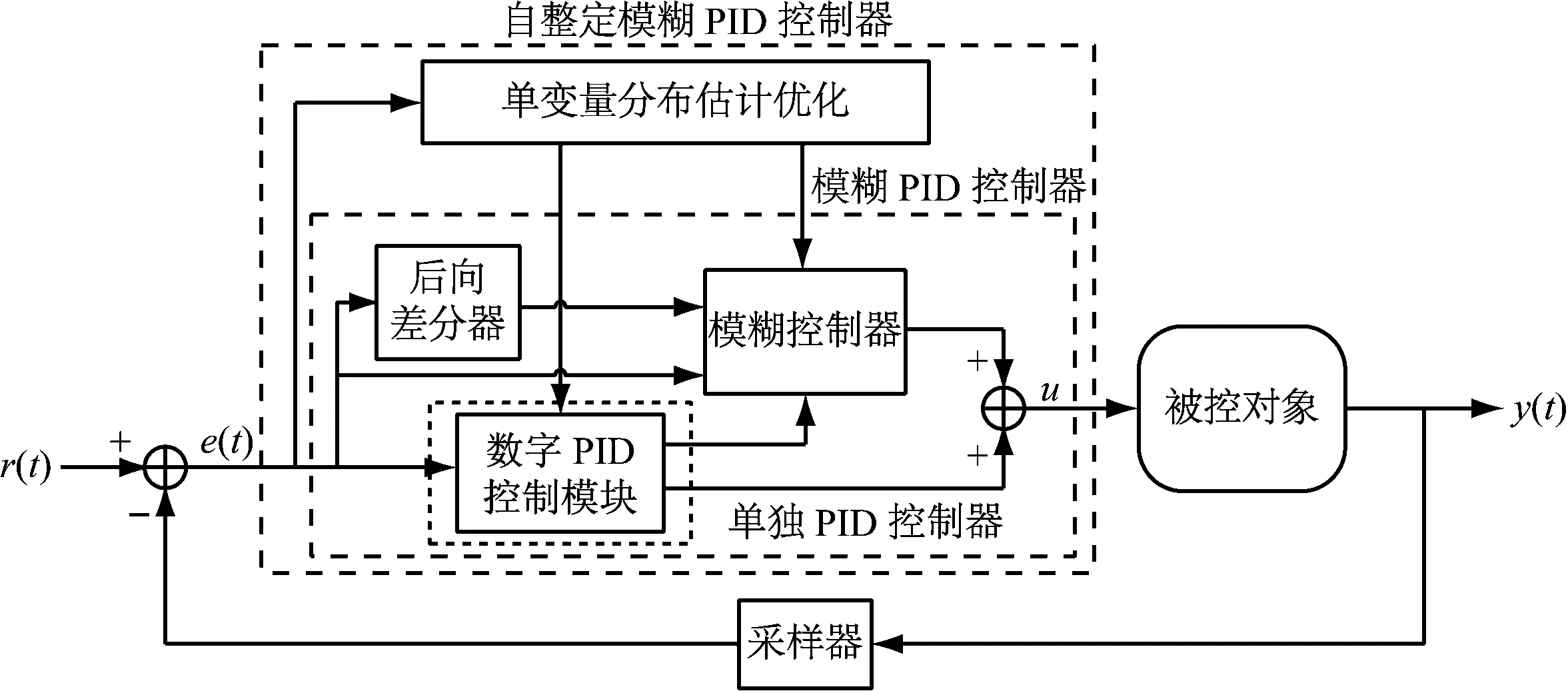
图2 主蒸汽温度控制器框架示意图Fig.2 Block diagram of the steam temperature controller

2.1 数字PID控制

PID是一种现行控制器，其根据给定输入与输出构成控制偏差，将偏差分别通过比例环节、积分环节和微分环节的线性组合构成控制量，对被控对象进行控制.其中PID控制器的输入是给定值r(t)与实际输出值y(t)形成的偏差量e(t)，即

(2)

PID控制器输出的控制量为：

(3)

式中：kP为比例系数；TI为积分系数；TD为微分系数，由被控对象的特性决定.

对式(3)进行周期为T的采样，将连续的时间t换成离散的采样时刻kT，积分用求和，微分用一阶向后差分近似，得到最终离散PID控制规则输出的表达式：

(4)

式中：u0(k)为第k个采样时刻的PID控制器输出；e(k)为第k个采样时刻的输出与输入间的偏差；积分系数kI=kPT/TI，微分系数kD=kPTD/T.其中，采样周期T要足够短以保证计算精度.

2.2 模糊控制器

模糊控制首次提出于1974年，其实质是一种非线性控制，从属于智能控制的范畴[15].模糊控制器的作用是通过模糊化、模糊推理和反模糊化过程，利用模糊规则库中的知识对PID控制模块的结果进行特定的修正，使其能达到实现更小的超调及更短的调整时间的目的.模糊控制器的输入量是系统输出与实际的偏差E和偏差的变化率Ec，输出量是与PID控制器的kP、kI和kD控制所对应的修正值集合u1(k)，该系统的结构框图见图3.

图3 模糊控制模块示意图Fig.3 Block diagram of the fuzzy control module

2.2.1 模糊化模块

输入量的模糊化模块中，目标采用模糊语言值{NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)和PB(正大)}来定义模糊变量E和Ec.模糊子集的隶属度函数采用高斯隶属度函数：

(5)

其中，x为输入变量，a、b为不同隶属度函数的参数，通过调整参数可以改变函数形状，以适应不同系统不同输入变量在不同值域时的控制要求，参数需由外部给出.通常，在模糊系统中输入变量(即E和Ec)的范围定义为其基本论域.

设E和Ec的模糊化论域分别为{-n,…, 0,…,n}与{-m,…, 0,…,m}，n、m分别为二者离散化后分成的档数，则将基本论域离散到模糊化论域的量化因子定义为：

(6)

2.2.2 解模糊化模块

对应于模糊化模块，使用加权平均法对输出量进行反模糊化，设输出量的精确值为o，则有：

(7)

式中：wi为输出量的模糊化论域值；μi为wi在各个模糊子集中对应的隶属度值.

继而需要把精确值缩放到PID控制器的论域内，参照上文的量化因子，设某PID控制器的基本论域为[-u,u]，定义比例因子如下：

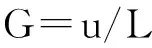
(8)

式中：L为其基本论域的量化档数，此处L=7.

2.2.3 模糊规则库

控制规则是模糊控制器的核心，直接影响到控制器的性能.针对受控系统的特点，采用自行设计的n=7、m=7的二维控制表，如表1～表3所示.其中ΔkP、ΔkI和ΔkD分别为ΔkP、TI和TD的变化量，即由偏差E和偏差变化率Ec得到的PID系数的修正值.

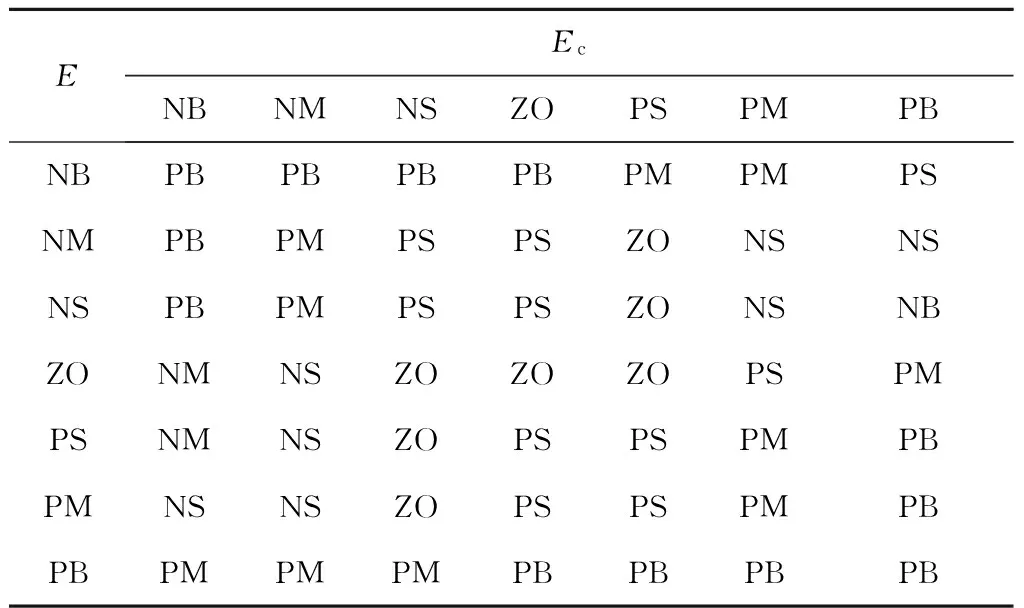
表1 ΔkP模糊控制规则表Tab.1 Table of fuzzy control rules for ΔkP

其中，ΔkP起主要调控作用，其主要设计思想是在偏差较大时加大调节力度，过渡过程中注意控制惯性，在稳态附近时偏向于PID控制；ΔkI和ΔkD亦可根据实际系统及需要自行设定.

2.2.4 模糊推理模块

以ΔkP为例，对于长度为n×m的模糊控制规则表，设其中的每条控制规则对应的模糊关系分别为R1,R2,…,Rn×m，则对于以{NB, NM, NS, ZO, PS, PM, PB}代表的7×7规则库，其计算公式如下：

(9)

将所有模糊关系合并为总模糊关系R，得：

(10)

最终基于Mamdani推理方法[16]，可以根据输入的模糊量E和Ec计算输出的模糊量ΔkP：

(11)

最终模糊系统对PID控制的修正输出为：

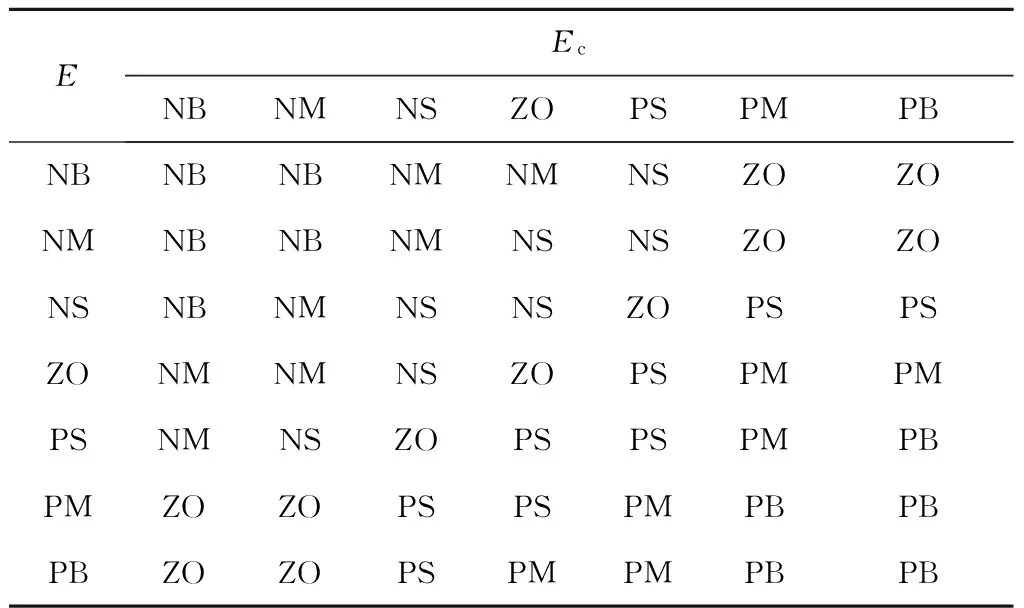
(12)表2 ΔkI模糊控制规则表Tab.2 Table of fuzzy control rules for ΔkI

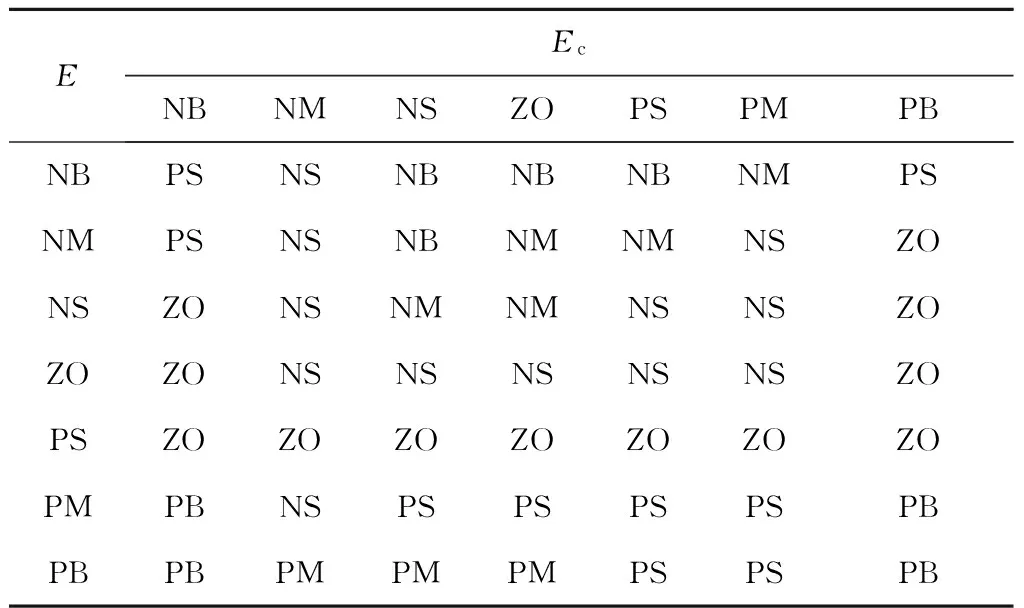
表3 ΔkD模糊控制规则表Tab.3 Table of fuzzy control rules for ΔkD

2.3 单变量分布估计优化

数字PID控制模块和模糊控制器都需要人为进行参数设置，不同参数对控制结果影响不同，而人为进行大量参数设置不仅需要耗费时间、人力成本，也对操作者的专业知识有较高的要求.为此，采用封装的单变量分布估计优化算法来实现参数的选择，自适应地实现系统参数的整定.

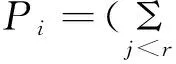
(1) 初始化种群q(0)，读取历史最优值加入初始种群，迭代次数t=0.

(2) 将q(t)按适应度值递减的顺序对染色体排序，并将前r个染色体作为精英保留.

(3) 计算前R(R一般大于r)个染色体每一列取1的概率Pi，组成概率矩阵.

(4) 以概率Pi随机产生一个符合0-1分布的数字作为染色体第i位，再用同样的算法生成(m-r)个染色体，将这些染色体和保留下来的r个染色体组成新的种群q(t+1).

(5) 令t=t+1，判断是否t>N.若是，则结束算法，若不是，则回到第二步.

其中，由于染色体的每一位对应一个二进制数值，对子模型权值进行优化时，权值需要经过编码才能参与分布估计运算.编码过程可简述为：初始化权值就是一组m×n维长的0和1编码序列，其中m为需要优化的权值个数，n为每个权值的编码位数，且每个权值的编码长度都是相同的.

同样，封装方法返回的优化结果需要经过与编码过程相对应的解码过程才能得到实际所需的权值结果.解码过程可简述为：权值wi的取值范围是[0,1]，假设第i个权值的编码是[q1q2…qn]，其中qi∈{0,1},i∈{1,2,…,n}，则：

(13)

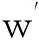
(14)

最终将wi乘以相应的量化因子即可.

对于2位模糊隶属度函数的选择，则直接将二进制编码转为十进制，即有wi=q1+2q2，解码为0表示使用均匀隶属度函数，为1表示使用三角形隶属度函数，为2或3表示使用高斯隶属度函数.

最终，将模拟信号引入封装框架，可以实现系统模型的训练和参数优化.训练并寻优后的系统即为本文的最终控制系统，综合式(4)和式(12)，系统输出的控制量u(k)=u0(k)+u1(k).

3 仿真实验结果与分析

以某火电厂锅炉变参数、大惯性、大时延的主蒸汽温度被控对象为例，系统导前区的传递函数为：

(15)

而惰性区的传递函数为：

(16)

以此进行仿真调整控制，输入信号为一个阶跃信号，分别得到使用单一PID控制(PID)、未优化的模糊PID控制(F-PID)以及单变量分布估计封装优化后的模糊PID控制(U-F-PID)时系统的输出及控制量.

图4和图5给出了3种控制算法下的输出结果.由图4可知，仅采用PID控制时，虽然系统最终也能稳定在目标值上，但产生了较显著的超调，且因震荡明显延长了调整时间；而在PID控制的同时增加了模糊控制的修正后，系统不仅快速地进行了响应，最终也能够稳定在目标值上，而且大幅消除了单独PID控制时的超调量，明显缩短了调整时间，但在模糊控制消除惯性的过程中带来了一次明显的震荡；在上述模糊PID控制的基础上采用UMDA进行自整定优化后，系统不仅快速地进行了响应，并最终稳定在目标值上，而且基本消除了单独PID控制时的超调量，明显缩短了调整时间，同时也消除了未优化的模糊控制带来的震荡.此外，由图5可知.本文方法的控制量变化比较平缓，发生的震荡次数较少.表4给出了3种控制算法下的阶跃响应性能，可见优化后的模糊PID控制效果最好.

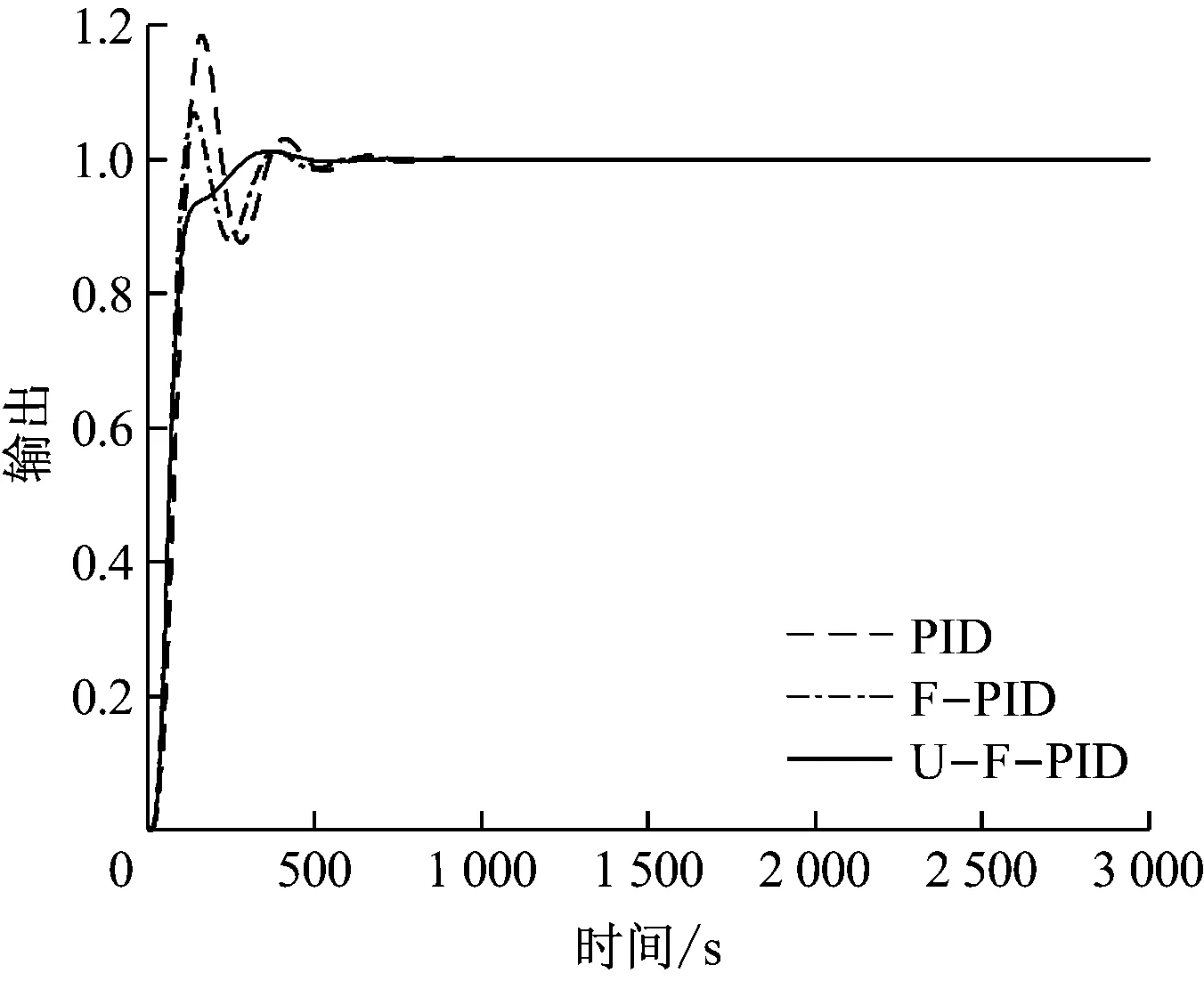
图4 不同控制算法下的阶跃信号输出Fig.4 Output results with step disturbance under different control algorithms

图5 不同控制算法下的总控制量输出Fig.5 Output quantity under different control algorithms

表4 不同控制算法的性能比较Tab.4 Comparison of control performance among different control algorithms

图6给出了摄动模型下3种控制算法的系统输出，其中导前区的传递函数变更为：

(17)

而惰性区的传递函数变更为：

(18)

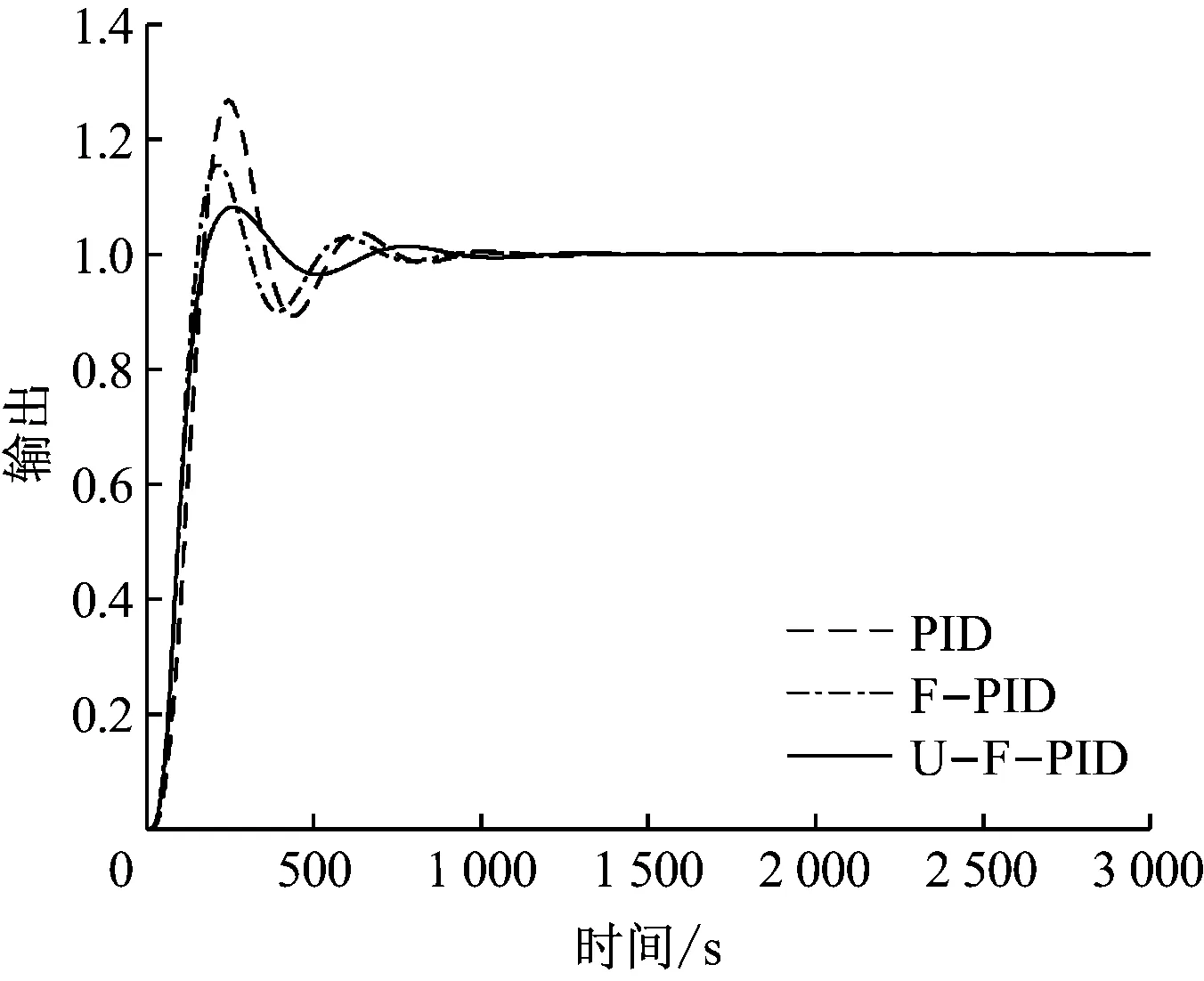
图6 不同控制算法下阶跃信号的摄动输出Fig.6 Output results with perturbation model under different control algorithms

由图6可知，参数变化对系统控制效果产生了很大影响，虽然未达到无摄动条件下的控制结果，使用单变量分布估计优化的模糊PID控制在摄动输入下仍然可以实现最小的超调量.同时模糊PID控制结果也优于普通的PID控制结果.

4 结 论

针对传统的PID控制在处理大滞后系统时效能的局限性以及参数整定的问题，研究设计了一种基于UMDA自适应整定的模糊PID控制系统，其最大优势就是能够针对被控对象快速自动调整控制器的参数，并且取得比传统控制方法更好的控制效果.

从仿真实验结果可以看出，采用所提出的控制方法系统响应曲线稳定性较好，调整时间短，无扰情况下不存在超调，摄动输入下也能明显地降低超调量，其控制效果明显优于原方法.该方法同样也可以应用于其他类似的工况不稳、大时滞系统的智能控制中，对于直流锅炉也有一定借鉴意义.

[1] 薛阳, 汪莎, 陈磊. 过热蒸汽温度控制中RBF神经网络整定PID控制的应用[J]. 上海电力学院学报, 2012, 28(5): 466-468, 477.

XUE Yang, WANG Sha, CHEN Lei. Application of RBF neural network-tuning PID control in superheated steam temperature control[J]. Journal of Shanghai University of Electric Power, 2012, 28(5): 466-468, 477.

[2] 贾立, 韩宇, 杨爱华. 基于Hammerstein模型的过热器系统建模[J]. 控制工程, 2013, 3(4): 276-281.

JIA Li, HAN Yu, YANG Aihua. Super-heater system modeling based on Hammerstein model[J]. Scientific Journal of Control Engineering, 2013, 3(4): 276-281.

[3] 谢克明, 侯宏仑, 谢刚. 过热汽温系统的自适应递阶模糊PID参数控制[J]. 中国电机工程学报, 2001, 21(9): 39-42.

XIE Keming, HOU Honglun, XIE Gang. An adaptive hierarchical fuzzy PID parameters control for superheated steam temperature system[J]. Proceedings of the CSEE, 2001, 21(9): 39-42.

[4] 马宁. 模糊PI控制在电厂串级汽温控制中的应用[J]. 电站系统工程, 2007, 23(3): 63-65.

MA Ning. Application of fuzzy PI and simulation modeling in power plant cascade steam temperature control system[J]. Power System Engineering, 2007, 23(3): 63-65.

[5] 杨平. 电站锅炉汽温控制研究进展[J]. 华东电力, 2009, 37(7): 1214-1218.

YANG Ping. Research progress on steam temperature control for power station boilers[J]. East China Electric Power, 2009, 37(7): 1214-1218.

[6] 雷俞芝, 杨晋萍, 郭向超. 基于模糊技术的锅炉主汽温控制系统研究[J]. 电力学报, 2013, 28(4): 345-348.

LEI Yuzhi, YANG Jinping, GUO Xiangchao. The control system research of boiler main stream temperature based on fuzzy technology[J]. Journal of Electric Power, 2013, 28(4): 345-348.

[7] XU Chengwei, LÜ Yongzai. Identification and self-learning of fuzzy models for dynamic systems[J]. Acta Automatica Sinica, 1988, 14(2): 135-140.

[8] WANG L X. Stable adaptive fuzzy control of nonlinear systems[J]. IEEE Transactions on Fuzzy Systems, 1993, 1(2): 146-155.

[9] 郝万君, 胡林献, 柴庆宣, 等. 基于专家PID的锅炉蒸汽压力控制策略[J]. 控制工程, 2005, 12(增刊1): 67-69, 128.

HAO Wanjun, HU Linxian, CHAI Qingxuan, et al. Control strategy for boiler steam pressure based on expert PID[J]. Control Engineering of China, 2005, 12(Sup1): 67-69, 128.

[10] 王恒飞, 陈永良, 郭春裕. 锅炉过热蒸汽出口压力的串级专家PID控制[J]. 自动化仪表, 2015, 36(10): 99-102.

WANG Hengfei, CHEN Yongliang, GUO Chunyu. Cascade expert PID control of boiler superheated steam outlet pressure[J]. Process Automation Instrumentation, 2015, 36(10): 99-102.

[11] 陈明杰, 兰海, 孙世峰. 遗传算法在锅炉蒸汽压力模糊PID控制中的应用研究[J]. 自动化技术与应用, 2008, 27(1): 12-16.

CHEN Mingjie, LAN Hai, SUN Shifeng. GA in fuzzy PID control of the boiler steam pressure[J]. Techniques of Automation and Applications, 2008, 27(1): 12-16.

[12] 汪阳华. 基于粒子群算法的锅炉主蒸汽压力模糊PID控制[J]. 湖南工业大学学报, 2012, 26(5): 62-66.

WANG Yanghua. Fuzzy PID control of boiler main steam pressure based on PSO[J]. Journal of Hunan University of Technology, 2012, 26(5): 62-66.

[13] 王朋, 刘林, 陈哲, 等. 基于改进DE算法的PID参数整定及其应用[J]. 动力工程学报, 2015, 35(3): 191-196.

WANG Peng, LIU Lin, CHEN Zhe, et al. PID parameter tuning based on improved DE algorithm and the application[J]. Journal of Chinese Society of Power Engineering, 2015, 35(3): 191-196.

[14] MÜHLENBEIN H, PAAβ G. From recombination of genes to the estimation of distributions. I. Binary parameters[C]//International Conference on Parallel Problem Solving from Nature. Berlin Heidelberg: Springer, 1996: 178-187.

[15] MAMDANI E H. Application of fuzzy algorithms for control of simple dynamic plant[J]. Proceedings of the Institution of Electrical Engineers, 1974, 121(12): 1585-1588.

[16] MAMDANI E H. Application of fuzzy logic to approximate reasoning using linguistic synthesis[J]. IEEE Transactions on Computers, 1977, 26(12): 1182-1191.

Fuzzy Self-tuning PID Control of Main Steam Temperature in Thermal Power Boilers Based on UMDA

WANGTiankun

(Shenhua Group Corporation Limited, Beijing 100011, China)

To solve the problem of large time delay and variable parameters in controlling the main steam temperature of thermal power boilers, a fuzzy self-tuning PID control algorithm was proposed based on univariate marginal distribution algorithm (UMDA), so as to improve the effectiveness of temperature control. For the given model of system with large time delay, fuzzy control rules were used to improve the PID controller, while parameters tuning was conducted by UMDA to achieve the optimization of the fuzzy PID controller, following which simulation and analysis were performed on the time-delay temperature control system. Results show that via the control algorithm proposed, there is basically no overshoot under normal working conditions, and the overshoot under perturbation conditions can be reduced remarkably, with obviously shortened adjustment time, indicating significant improvements on the performance of original system.

temperature control; fuzzy PID; UMDA

2016-06-23

2016-08-09

王天堃(1982-)，男，吉林德惠人，高级工程师，博士，主要从事生产管理、火力发电厂先进控制技术、分散控制系统、现场总线控制系统方面的研究．电话(Tel．)：18911898376；E-mail: 17000107@shenhua.cc．

1674-7607(2017)07-0546-06

TK32

A

510.80