基于内分泌单神经元滑模的核电站稳压器控制
赵 明, 叶建华, 李晨晶, 陈鹏飞
(上海电力学院 自动化工程学院, 电站自动化技术重点实验室,上海 200090)
基于内分泌单神经元滑模的核电站稳压器控制
赵 明, 叶建华, 李晨晶, 陈鹏飞
(上海电力学院 自动化工程学院, 电站自动化技术重点实验室,上海 200090)
针对系统较为复杂的核电站稳压器,在生物神经内分泌腺体激素调节的原理上,设计了一种包含长反馈和超短反馈的双层控制器.在内模和滑模复合控制系统中,内模控制器即内分泌单神经元PID负责控制系统的跟踪性能,滑模控制器负责消除系统的干扰.引入模糊控制整定单神经元PID的输出增益,建立稳压器压力和水位控制的仿真模型.结果表明:内分泌变增益单神经元滑模的控制器相较于传统PID控制器具有更加优良的性能.
稳压器; 内分泌; 单神经元PID; 滑模控制; 模糊控制
稳压器可调节和维持一回路冷却剂的压力,是核电站一回路的重要设备之一.系统负荷变化等扰动会影响稳压器压力和水位的变化,若稳压器不能得到有效控制,将给核反应堆的安全运行带来隐患.目前,稳压器常用的控制有PID控制和模糊控制等.对于传统PID控制,系统虽然响应速度比较慢,但稳态性能较好[1];而模糊控制正好相反,系统虽然响应速度较快,但稳态误差较大[2].综上所述,笔者设计了一种基于内分泌变增益单神经元PID(内模)滑模的控制器.利用内模控制能消除不可测干扰的影响,系统跟踪性能较好.当被控对象或系统中存在模型摄动和外部扰动时,内模与滑模的复合控制在一定条件下具有很强的稳健性[3],可实现消除干扰的目的.笔者将稳压器的跟踪性和稳健性分开进行设计,获得了比传统PID更好的控制性能,实现了核电站稳压器的最佳控制.
1 内模与滑模控制的结合
1.1 内模控制的基本原理
内模控制(Internal Model Control, IMC)是一种基于过程数学模型进行控制器设计的新型控制策略,其最大特点是把跟踪性能与稳健性能问题分开处理,简化了分析、设计和调整过程[4].其典型的控制结构如图1所示.

图1 内模控制原理图Fig.1 Principle diagram of the internal model controller
图1中:P(s)为被控过程;M(s)为被控过程的数学模型,即内部模型;Q(s)为内模控制器;r、y和d分别为系统的输入、输出和干扰信号;u(s)和ym分别为控制输出量和内部模型的输出;“+”、“-”分别表示系统的正负反馈作用;C(s)为反馈控制器.
由等效反馈可知:
(1)
(2)
1.2 滑模控制的基本原理
滑模变结构是一种随时间变化的不连续的控制,其运动可分为2个部分:一是运动段,二是滑模段.控制律一般由保证系统状态在滑模面上的等效控制ueq和保证系统状态不离开滑模面的切换控制uvs组成[5].该控制系统不受参数变化和外界干扰的影响,表现出极强的稳健性.滑模控制的不连续性造成了系统的抖振.
考虑如下n阶非线性系统:
(3)
(4)
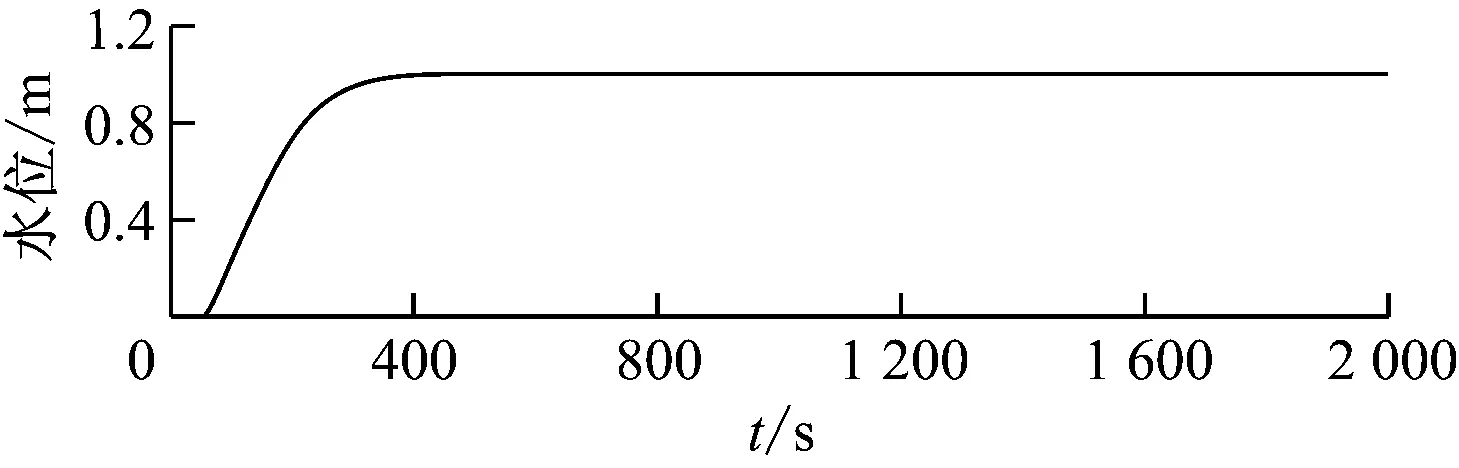
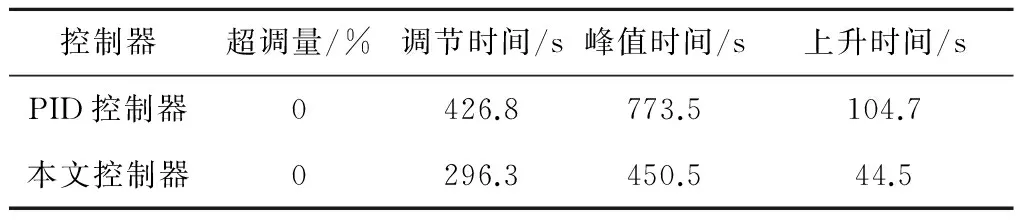
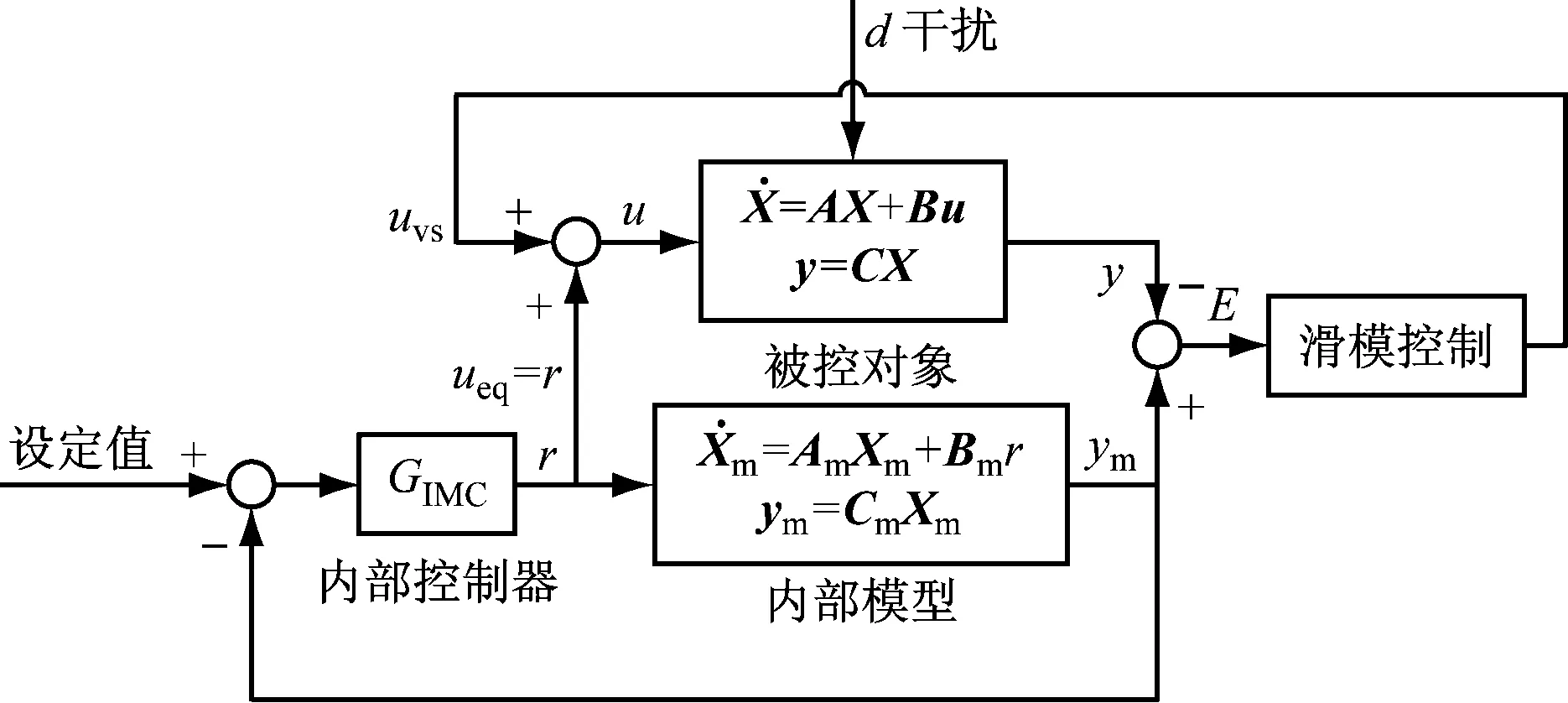
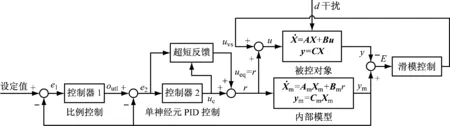
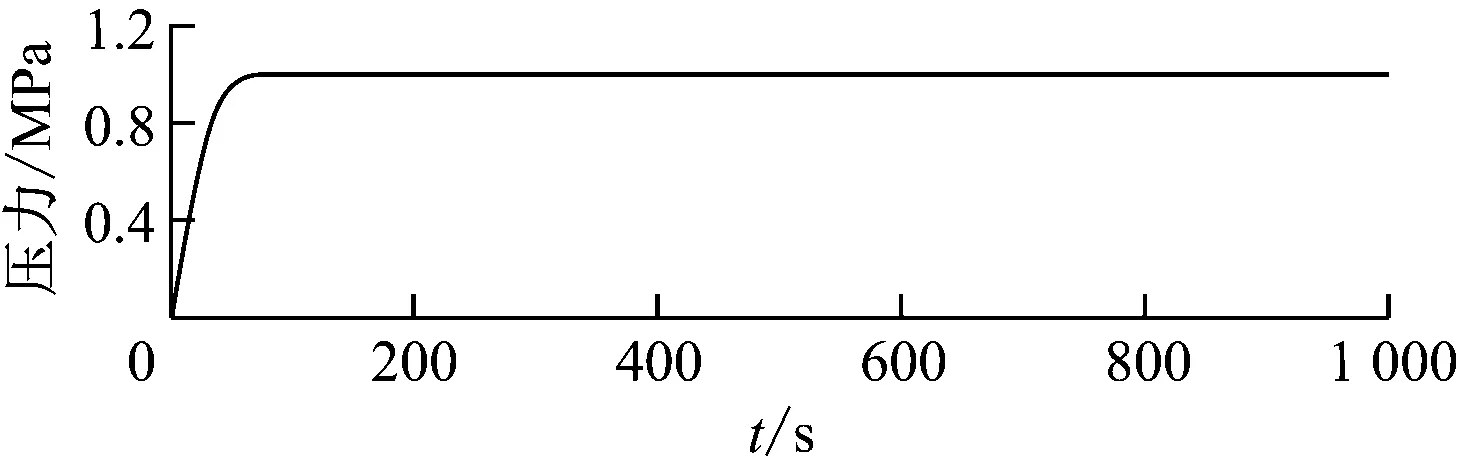
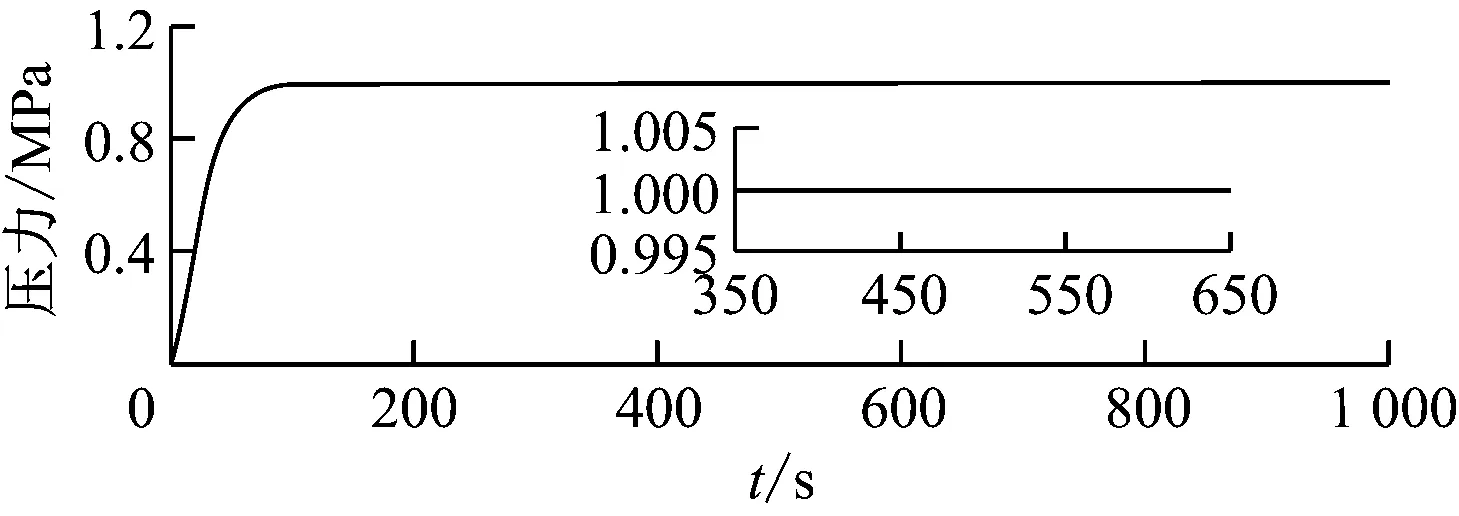
式中:f(x,t)为已知的函数,b>0;状态向量x为n×1的列向量,其中状态变量x∈R;输入变量u∈R;输出变量y∈R;d(t)为外加干扰,且|d(t)| 1.2.1 等效控制 在不考虑扰动时,被控对象为: (5) 跟踪误差向量为: (6) 式中:xd为系统理想的输入信号. 切换函数设计为: (7) 式中:切换矩阵C1=[c1c2…cn-11]. 取s′=0,则 s′(x,t)=c1e′+…+e(n)=c1e′+…+ f(x,t)-bu(t)=0 (8) 式中:s′(x,t)为切换函数的导数;c1,c2,…,cn-1为切换矩阵的分量;e′,…,e(n)为跟踪误差向量的分量,即误差的各阶导数. 等效控制器设计为: (9) 1.2.2 滑模控制 (10) 为了消弱抖振,用饱和函数sats代替式(10)中的符号函数sgns: (11) 其中,Δ称为“边界层”,即s取值的一个小范围. 同时,采用改进的指数趋近律: (12) 最终的滑模控制律为:u=ueq+uvs(g) (13) 定义Lyapunov函数: (14) (15) 1.3 内模与滑模的复合控制 内模滑模复合控制的基本原理图[6]见图2. 图2 内模滑模复合控制结构图Fig.2 Structure diagram of the internal model and sliding mode compound controller (16) 由内模控制理论可知,内部模型就是被控对象的标称模型.故当给定的参考模型与被控对象的标称模型相同时,参考模型可看作被控对象的内部模型,即 (17) 故当滑模切换面S=C1E=C1(ym-y)=0时,有ym=y,实现了被控对象的输出对给定内部模型输出的跟踪.其中ym、y分别为内部模型对象和被控对象的输出. 此时,滑模的等效控制可表示为: ueq=(C1CmBm)-1C1Cm(AmXm+Bmr-AmXm)= (C1CmBm)-1C1CmBmr=r (18) 由ueq的特殊形式,当给定参考模型与被控对象的内部模型相等时,ueq即为给定参考模型的输入.被控对象不确定部分或干扰由滑模控制到达段的切换控制uvs来消除.因此,以上由内模与滑模相结合的控制器的控制律为: (19) 由于内模滑模复合控制结构是一种最基本、最简单的形式,在此基础上,基于状态反馈u=KTX(K为状态反馈矩阵)设计了内模滑模复合控制系统.理论推导与上面类似,具体参考文献[6],其结构图如图3所示. 2.1 内分泌系统的激素调节机制 生物体内的下丘脑、垂体和腺体组成了体内内分泌激素调节系统.其调节原理的反馈环节包括长反馈(即常规反馈)和超短反馈.下丘脑分泌的促激素(TRH)刺激垂体分泌促甲状腺素(TSH),进而刺激甲状腺分泌甲状腺激素.甲状腺释放的甲状腺激素(T3、T4)反过来同时作用于下丘脑和垂体,影响其对应激素的分泌,形成长反馈回路;垂体释放的促甲状腺素不仅影响甲状腺,而且影响自身,形成超短反馈[7].其工作原理如图4所示. 图3 基于状态反馈的内模滑模复合控制结构图 Fig.3 Structure diagram of the internal model and sliding mode compound controller based on state feedback 图4 甲状腺激素调节回路Fig.4 Thyroid hormone regulation loop 2.2 内分泌控制器结构 由内分泌系统的激素调节机制可以得到图5所示的双层控制器结构.其中,e1为一级控制器的误差,e2为二级控制器的误差,out1为一级控制器的输出,uc为控制器2的输出.这种双层控制最大的优点是能够实现系统的快速跟踪性能.其中,一级控制器用于不断调整二级控制器的输入,快速、稳定地消除系统偏差;超短反馈控制器的作用是根据误差大小来补偿,按照激素分泌规律动态补偿控制输出,实现更好的控制性能.与传统串级控制最大的不同是其反馈量输入不同. 图5 内分泌两级控制器结构Fig.5 Structure diagram of the two-stage endocrine controller 2.2.1 一级控制器控制规律 对于一级控制器的控制规律,可以根据传统串级控制主控制器的规律进行选择.笔者选择比例控制,目的是实现系统的快速跟踪性.一级控制器的输出out1在给定值r附近随着偏差e1的改变而改变,当偏差e1=0时,其输出值为给定值r,相应表达式如下: e1=r-y (20) (21) 式中:kp1>0,为一级控制器的比例系数. 在一定范围内,随着比例系数的增大,系统快速跟踪性越显著,但同时也会带来系统的超调和振荡.在实际情况下,参数的选择和调整与传统串级控制系统类似,首先投入二级控制器使控制曲线略接近振荡状态,以保证二级控制器的迅速反应能力.然后再投入一级控制器,调整比例系数kp1,直到控制效果满足要求为止. 2.2.2 二级控制器的控制规律 传统二级控制器为PID控制,其自适应能力有限.相比于传统PID控制,改进单神经元PID控制性能更加优越,尤其对存在复杂控制对象的系统,其自学习和自适应能力表现得更好.图4中误差信号e2先在单神经元控制器内部转换为单神经元的输入信号xi(k),i=1,2,3: (22) 二级控制器采用改进的单神经元控制,其控制算法如下: (23) 式中:ηI、ηP、ηD分别为积分、比例、微分的学习速率;K为神经元的比例系数.通常K值的大小对控制系统的性能指标影响较大. 由于单神经元控制中k值对控制器的影响较大,对比例系数K引入了基于模糊控制的策略,对K值进行在线自整定.同时,采用两输入-输出形式,以稳压器的压力或水位的误差e和误差的导数ec作为输入变量,输出变量为单神经元PID控制器的比例系数K. 根据实际情况和经验,e和ec变化范围在模糊集上的论域为{-5,-4,-3,-2,-1,0,1,2,3,4,5},比例系数K的论域为{-3,-2,-1,0,1,2,3}.其模糊子集={NB、NM、NS、ZO、PS、PM、PB},对应{负大、负中、负小、零、正小、正中、正大}.e、ec和k均服从正态分布,模糊规则表可参考文献[8]. 2.2.3 超短反馈控制律 超短反馈采用内分泌调节规律,将控制器2(变增益单神经元PID控制器)的当前输出变化量Δuc(k)作为超短反馈的输入信号,根据Farhy[9]提出的激素腺体分泌激素的通用规律对控制变化量Δuc(k)进行超短反馈处理,得到非线性反馈的函数: (24) (25) 式中:a、n为因子系数,决定了超短反馈补偿的幅度;b决定了超短反馈补偿的方向.以变增益单神经元PID控制的变化量Δuc(k)作为激励信号,最后二级控制器的输出u(k)为: (26) 实际应用中存在许多扰动,控制系统不太容易实现理想的性能指标.因此,将因子系数a进行分段处理[10],以减小超短反馈对二级控制器输出造成的影响.分段处理后的因子系数a'为: (27) 根据前面的理论分析,设计了内分泌单神经元滑模控制器,其总体框图如图6所示.系统的跟踪性由被控对象的内部模型决定,且内部模型的给定输入r为滑模控制的等效控制ueq,也是内分泌单神经元PID的输出.系统的稳健性由滑模的切换作用uvs保证,以消除被控对象参数的变化和扰动.系统采用的被控对象的内部模型可以使系统在刚开始就能处于滑模面上,即不存在趋近阶段,使被控对象一直在滑模的切换作用uvs下跟踪内部模型. 某核电站稳压器压力和水位控制系统的数学模型[1]如下: 稳压器压力控制系统模型: (28) 图6 控制系统总体框图Fig.6 Overall block diagram of the control system 稳压器水位控制系统模型: (29) 采用内模滑模的压力控制方法,改进单神经元PID的控制参数:ηP=7 000,ηI=42.254 55,ηD=65 520;超短反馈参数:a=30,n=1.5;滑模控制参数:c=10,ε=0.125,k=1 100;外界干扰信号为sint;同时放大压力(10.05 MPa)和时间(300~700 s)范围的局部图,系统稳健性的仿真结果如图7所示. (a) 不加扰动的输出 (b) 加扰动的输出 (c) 加扰动滑模的输出图7 内分泌变增益单神经元的压力跟踪误差比较 Fig.7 Comparison of pressure tracking error of endocrine variable gain single neuron 在500 s时给系统一个幅值为0.1的阶跃干扰,并与传统PID控制进行对比,得到系统跟踪性仿真结果如图8所示. 由图7和图8的仿真结果可知,当系统存在扰动时,系统的稳健性完全由滑模控制决定,且系统的跟踪性能不受影响.系统的跟踪性能由内模控制器决定,即本文的内分泌变增益单神经元控制器.通过表1可以清楚地看到,与传统PID控制相比,内模滑模控制系统的调节时间、峰值时间和上升时间均大幅缩短,具有较好的响应特性和控制速度. 图8 压力控制系统的仿真结果Fig.8 Simulation results of the pressure control system表1 控制器动态性能的比较(压力) Tab.1 Comparison of dynamic performance between two controllers (pressure) 控制器超调量/%调节时间/s峰值时间/s上升时间/sPID控制器0134.5394.3104.7本文控制器052.889.444.6 采用内模滑模的水位控制方法,改进单神经元PID的控制参数:ηP=150,ηI=0.575,ηD=15;超短反馈参数:a=20,n=2;滑模控制参数:c=5,ε=0.35,k=0.001 25;外界干扰信号为5sint;同时放大水位(10.05 m)和时间(800~1 200 s)范围的局部图,系统稳健性仿真结果如图9所示.本文控制器与传统PID控制器的系统跟踪性仿真结果如图10所示. 由图9和图10可以看出,当系统存在环境扰动时,滑模控制可消除系统干扰和参数的摄动等,同时对系统的跟踪性能不产生影响.而系统的跟踪性能由内模控制器决定,即本文的内分泌单神经元控制器.由表2可以清楚地看到,相比于传统PID控制,基于内分泌变增益单神经元PID滑模的控制器的调节时间、峰值时间和上升时间均较短,稳态误差较小,控制精度高,能够提高稳压器水位的控制性能. 针对系统较为复杂的核电站稳压器,设计了内模滑模控制器,可实现有效的稳压器压力和水位的控制.仿真结果表明:基于内分泌变增益单神经元PID滑模的控制器可以使系统达到更加优良的性能指标. (a) 不加扰动的输出 (b) 加扰动的输出 (c) 加扰动滑模的输出图9 内分泌变增益单神经元的水位跟踪误差比较 Fig.9 Comparison of water level tracking error of endocrine variable gain single neuron 图10 水位控制系统仿真结果Fig.10 Simulation results of the water level control system表2 控制器动态性能的比较(水位) Tab.2 Comparison of dynamic performance between two controllers (water level) 控制器超调量/%调节时间/s峰值时间/s上升时间/sPID控制器0426.8773.5104.7本文控制器0296.3450.544.5 [1] 林静.基于自抗扰的核电站稳压器控制系统研究[D].上海:上海电力学院,2014. [2] 李永铃,黄宇,马进,等.核电站稳压器内模PID优化控制[J].动力工程学报,2013,33(11):858-863. LI Yongling, HUANG Yu, MA Jin, et al. Optimization on internal model PID control for nuclear power pressurizers[J].Journal of Chinese Society of Power Engineering,2013,33(11):858-863. [3] 柴华伟,马大为,李志刚,等.交流伺服系统最优内模滑模控制器设计与应用[J].南京航空航天大学学报,2007,39(4):510-513. CHAI Huawei, MA Dawei, LI Zhigang, et al. Design and application of optimal IMC-SMC in AC servo systems[J].Journal of Nanjing University of Aeronautics & Astronautics,2007,39(4):510-513. [4] 赵志斌,文新宇.內模控制及其应用[M].北京:电子工业出版社,2012. [5] 刘金琨.滑模变结构控制MATLAB仿真[M].2版.北京:清华大学出版社,2012. [6] 王有庆.基于内模滑模复合控制的直线电机高性能伺服控制研究[D].上海:上海交通大学,2003. [7] 黄桓.六自由度并联机器人内分泌控制策略的研究[D].上海:东华大学,2009. [8] 陈杰,陈冉,陈家伟,等.变速风力发电机组的模糊-单神经元PID控制[J].中国电机工程学报,2011,31(27):88-94. CHEN Jie, CHEN Ran, CHEN Jiawei, et al. Fuzzy single-neuron PID control of variable-speed wind turbines[J]. Proceedings of the CSEE, 2011, 31(27): 88-94. [9] FARHY L S. Modeling of oscillations in endocrine networks with feedback [J]. Methods in Enzymology, 2004, 384: 54-81. [10] 张嵩.基于神经内分泌反馈机制的模糊PID串级主汽温度控制系统研究[D].保定:华北电力大学,2012. Nuclear Power Plant Pressurizer Control Based on Sliding Mode of Endocrine Single Neuron ZHAOMing,YEJianhua,LIChenjing,CHENPengfei (Key Laboratory of Power Station Automation Technology, School of Automation Engineering,Shanghai University of Electric Power, Shanghai 200090, China) Based on the principle of biological neuroendocrine gland hormone regulation, a double layer controller containing long feedback and ultra-short feedback was designed for the nuclear power plant pressurizer with relatively complicated system. In the inner model and sliding mode compound control system, the tracking performance was realized by the internal model controller, namely the endocrine single neuron PID, while the interference of the system was eliminated by the sliding mode controller. A fuzzy controller was introduced to regulate the output gain of signal neuron PID, and a simulation model was established to control the pressure and water level of the pressurizer. Results show that the endocrine variable gain single nerve sliding mode controller has better performance than the traditional PID controller. pressurizer; endocrine; single neuron PID; sliding mode control; fuzzy control 2016-05-03 2016-08-04 上海市电站自动化技术重点实验室资助项目(13DZ2273800) 赵 明(1991-),男,安徽合肥人,硕士研究生,主要从事核反应堆稳压器先进控制方面的研究.电话(Tel.):15221512453; E-mail:1158111495@qq.com. 1674-7607(2017)07-0552-06 TL361 A 510.80
2 神经内分泌智能控制器设计


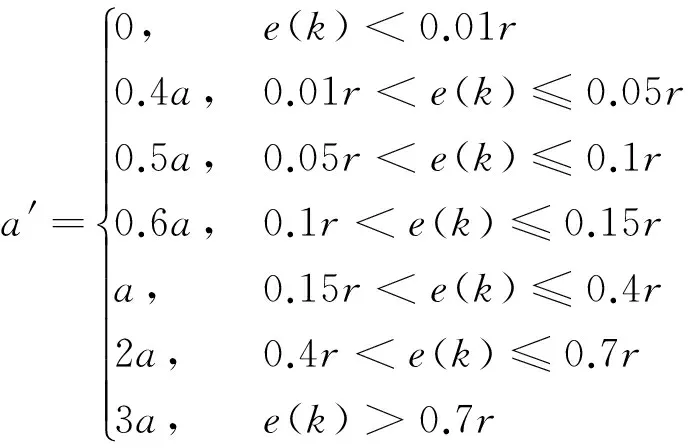
3 控制系统总体框图
4 系统仿真



5 结 论