广义犹豫模糊软集
黄 鹤,王艳平
(辽宁工业大学 理学院,辽宁 锦州121001)
广义犹豫模糊软集
黄 鹤,王艳平
(辽宁工业大学 理学院,辽宁 锦州121001)
将广义模糊软集和犹豫模糊软集相结合,提出广义犹豫模糊软集的概念,既避免广义模糊软集模型信息丢失,又弥补犹豫模糊软集在参数集不同时无法进行交并运算的缺点。首先提出广义犹豫模糊软集定义,然后给出广义犹豫模糊软集的并、交、补运算的定义,接着讨论运算的性质,并给出了广义犹豫模糊软集De Morgan律的证明。最后通过实例验证定义的有效性。
犹豫模糊软集;广义模糊软集;广义犹豫模糊软集
社会和科技不断进步,许多领域涉及到的数据愈发庞大、复杂以及不确定,比如医学、经济学和环境科学等。为了从这些庞大复杂不确定的数据中提取出隐含的有用信息,来自数学和计算机科学等领域的一些专家学者提出了许多处理不确定问题的数学理论和工具。针对数据的复杂庞大不确定性等问题,Zadeh教授[1]在1965年提出的模糊集理论,俄罗斯数学家Molodtsov[2-3]于1999年提出的软集理论,以及西班牙学者Torra[4]提出的犹豫模糊集理论都很好地解决了以上问题。
后来学者们陆续提出了模糊软集[5-6]、犹豫模糊软集[7]、广义模糊软集[8]等数学理论,使解决不确定性、不完善性等问题的方法进一步得到了升华。在文献[9]中作者考虑到了关于软集(F,E)中属性集E的权重iω情况,但不够细化。在文献[10]中作者将区间值模糊软集做了推广,考虑到了参数权重的不确定性,使决策系统化。受此启发,本文研究犹豫模糊集与广义模糊软集相结合的情况,考虑到犹豫模糊集具有信息完备性的特点,提出广义犹豫模糊软集模型,并给出其基本定义,然后针对参数集不同的广义犹豫模糊软集间的交、并、补运算进行讨论。
1 预备知识
首先,回顾一下Maji提出的模糊软集。
定义1[5]设U是有限论域,E是参数集合,A⊆E,是U的所有模糊子集组成的集合,称二元组(F,A)是U上的模糊软集(Fuzzy soft set),其中F是从A到的映射,即F:,称(F,A)为模糊软集。
在此基础上,Wen[7]定义了下面的犹豫模糊软集。并给出了犹豫模糊软集的包含关系,以及并、交和补运算。
定义2[7]设U为一个论域,E为属性集,是U上的全体犹豫模糊集,为一个映射:
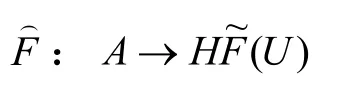
定义3[7]记为犹豫模糊软集的补集,定义为:
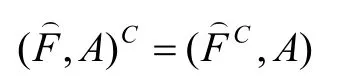
定义4[7]对于U上的两个犹豫模糊软集和,及,若满足:
定义5[7]论域U上的两个犹豫模糊软集和,当且时,称犹豫模糊软集和相等,记为:
定义6[7]对于U上的两个犹豫模糊软集和,“”表示为两个犹豫模糊软集的并。其中,C=A∪B,且∀ε∈C,有:
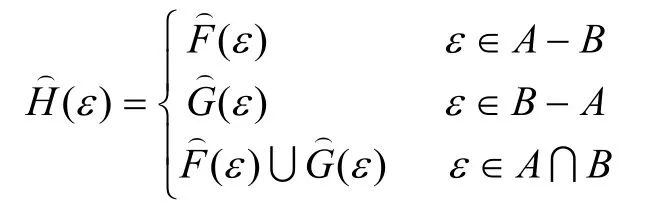
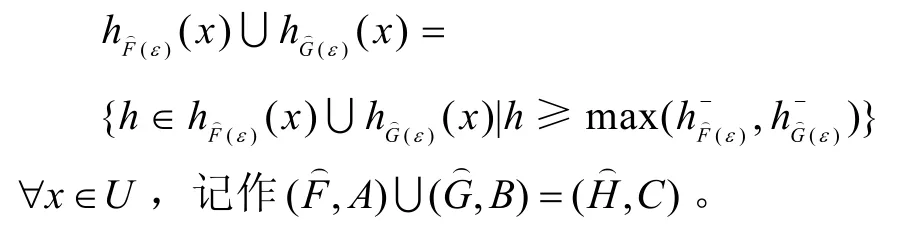
定义7[7]对于U上的两个犹豫模糊软集表示为两个犹豫模糊软集的交。其中C=A∩B,C≠φ且∀ε∈C,有:,其中和分别代表犹豫模糊集和中的犹豫模糊元。
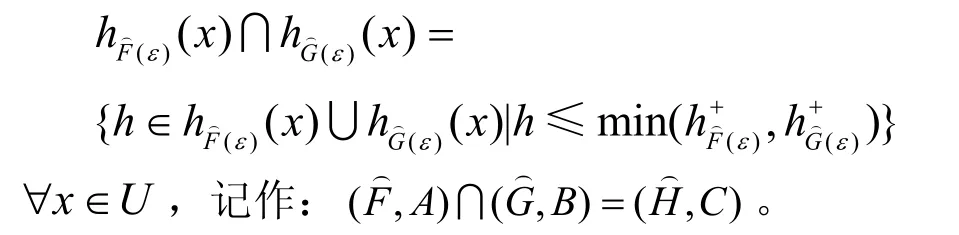
Majumdar和Samanta又提出了广义模糊软集,定义如下。
定义8[8]设U是初始论域,E是参数集,F:是一个映射,λ是E的模糊子集,即:。定义映射Fλ:,使得:
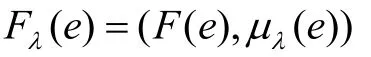
2 广义犹豫模糊软集
本节将犹豫模糊集理论与广义模糊软集相结合,给出广义犹豫模糊软集的相关定义。
定义9设U为初始论域,E为参数集,是一个映射,α是A的一个犹豫模糊子集,即:
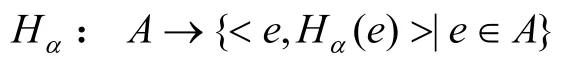
其中Hα为参数e对应的犹豫模糊元。定义函数使∀e∈E:
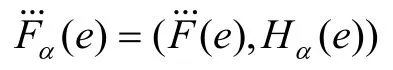
下面通过一个具体的例子来说明上述定义。

3 广义犹豫模糊软集的并交补运算及其性质
根据上一节给出的广义犹豫模糊软集定义,本节将讨论广义犹豫模糊软集的交并补运算及其性质。为了方便定义运算,需要对定义9进行改进,为此先定义两种特殊的犹豫模糊集。
定义12[11]设U为初始论域,定义空犹豫模糊集和满犹豫模糊集如下。
(1)空犹豫模糊集Hφ:对∀x∈U,Hφ(x)={0}。
(2)满犹豫模糊集HU:对∀x∈U,HU(x)={1}。
在许多文献中软集间进行交并运算时并未考虑到参数集不相同的情况,针对这个问题,本文给出下面定义。
定义13设U为初始论域,E为参数集,为一个广义犹豫模糊软集,将扩充到,令,即对∀e∈E,当e∈A时,当e∉A时,,则称为的扩充。
定义14设U为初始论域,定义两种特殊的广义犹豫模糊软集,分别为:广义空犹豫模糊软集和广义满犹豫模糊软集,定义形式如下:
(1)广义空犹豫模糊软集:对 ∀e∈E,,记为
(2)广义满犹豫模糊软集:对 ∀e∈E,,记为。
定义15对于U上的两个广义犹豫模糊软集和,对应的扩充为和。对∀ε∈E,有:
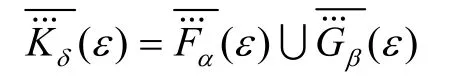
其中,h为广义犹豫模糊软集中的犹豫模糊元。

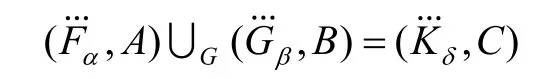
定义16对于U上的两个广义犹豫模糊软集和,对应的扩充为和。对∀ε∈E,有:
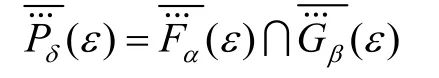
其中,h为广义犹豫模糊软集中的犹豫模糊元。
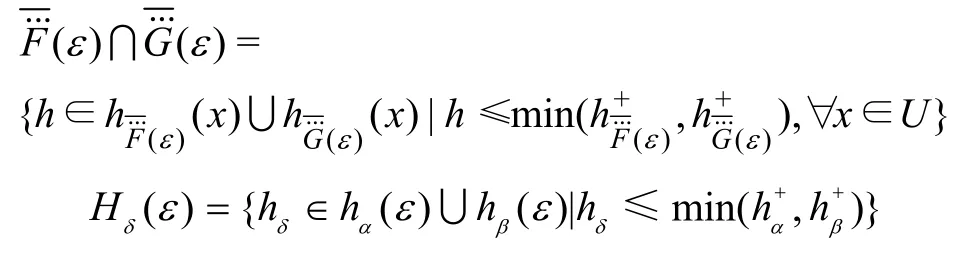

定义17(补集)论域为U,参数集为E,。为广义犹豫模糊软集,其对应的扩充为。定义:
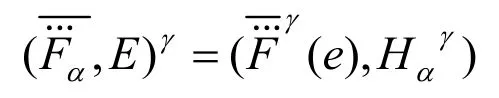
对∀e∈E有:
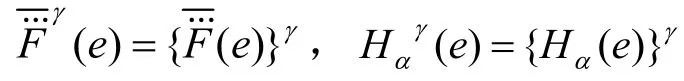
由定义15和16不难看出,它们与定义6和7的形式是完全一致的。但在定义13的基础上定义广义犹豫模糊软集的交并补运算更为简单,而且具有统一性。由上述定义及犹豫模糊集的运算性质不难得到以下性质。
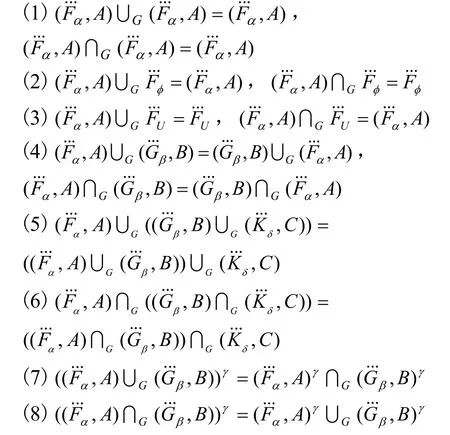
下面只就性质(7)给出证明,其余由定义直接可得或类似可证。


其中:

设乙考虑的参数只有B={耐用的,功能多的},则:
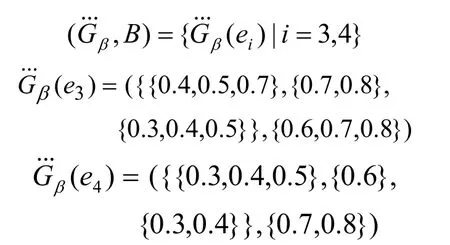
由定义13可得到扩充后的两个广义犹豫模糊软集:


由定义16可得到两个广义犹豫模糊软集的交
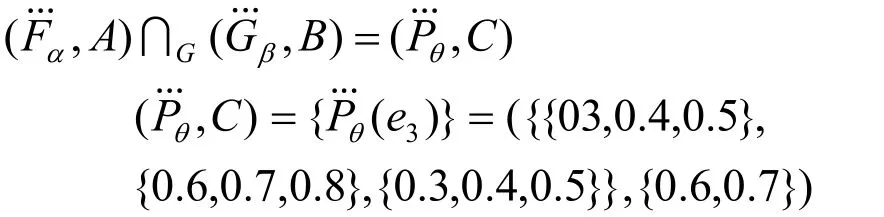


通过上例可以看出,与定义6和7比较,虽然它们在本质上是一样的,但本文定义的广义犹豫模糊软集的交并补运算更加直观。
4 结束语
软集的应用愈发广泛,其理论的深入研究亦变得愈发必要。本文把广义模糊软集的思想推广到犹豫模糊软集,提出了广义犹豫模糊软集,这是广义模糊集合与犹豫模糊集合的进一步推广。广义犹豫模糊软集不仅可以更完善地处理信息,更能够计算有不同参数集的两个广义犹豫模糊软集间的交并运算。本文在定义的基础上讨论了广义犹豫模糊软集的并、交、补运算及其运算性质。广义犹豫模糊软集的并交补运算具有简单明了的运算特点。
本文进一步完善了软集理论,为实际应用奠定了基础。
[1]Zadeh LA.Fuzzy sets[J].Information and Control,1965,8: 338-353.
[2]Molodtsov D.Soft set theory-First results[J].Computers and Mathematics withApplications,1999,37:19-31.
[3]Molodtsov D.The theory of soft set[M].Moscow:URSS Publishers,2004.
[4]Torra V,Narukawa Y.On hesitantfuzzy setsand decision[C].In:The 18th IEEE Int Conf Fuzzy Systems, JejuIsl-and,Korea,2009:1378-1382.
[5]Maji P K,Biswas R,Roy A R.Fuzzy Soft Sets[J].The Jurnal of Fuzzy Mathematics,2001,9(3):589-602.
[6]Maji P K,Biswas R,Roy AR.Soft set theory[J].Computers and Mathematics withApplications,2003,45:555-562.
[7]Wen X.Hesitant fuzzy soft sets[J].Computer Engineering andApplications,2015,51(24):56-60.
[8]Majumdar P,Samanta S K.Generalised fuzzy soft sets[J].Comput MathAppl,2010,59(4):1425-1432.
[9]温永川,关于软集的研究[D].大连:辽宁师范大学, 2008.
[10]周小强,软集与犹豫模糊集理论及其在决策中的应用[D].长沙:湖南大学,2014.
[11]Torra V.Hesitant fuzzy sets[J].International Journal of Intelligent Systems,2010,25(6):529-539.
[12]Zhu B,Xu Z,Xia M.Dual hesitant fuzzy sets[J].Journal ofApplied Mathematics,2012,26(5):410-425.
[13]Ju Y,Liu X,Yang S.Interval-valued dual hesitant fuzzy aggregation operators and their applications to multiple attribute decision making[J].Journal of Intelligent and Fuzzy Systems,2014,27(3):1203-1218.
责任编校:孙 林
Generalized Hesitant Fuzzy Soft Set
HUANG He,WANG Yan-ping
(Science College,Liaoning University of Technology,Jinzhou 121001,China)
The generalized hesitant fuzzy soft sets are proposed by combining generalized fuzzy soft sets with hesitant fuzzy soft sets in this paper.In generalized hesitant fuzzy soft sets, the information loss and being unable to calculate basic operations of union and intersection can be avoided while the parameter set is different.At first,some basic operations of union,intersection and complement are studied and fundamental properties of generalized hesitant fuzzy soft sets are discussed as well.Meanwhile,the De Morgan’s law of generalized hesitant fuzzy soft sets is proved.A practical example is given to illustrate the effectiveness of the definition.
hesitant fuzzy soft sets;generalized fuzzy soft sets;generalized hesitant fuzzy soft set
TP301;O236
A
1674-3261(2017)01-0062-05
2016-03-31
黄 鹤(1991-),男,辽宁沈阳人,硕士生。
王艳平(1965-),女,辽宁锦州人,教授,硕士。
10.15916/j.issn1674-3261.2017.01.016

