左截断右删失数据下非参数估计方法的研究*

陈金宝 侯雅文 陈 征△



左截断右删失数据下非参数估计方法的研究*

陈金宝1侯雅文2陈 征1△

目的 针对左截断右删失数据，现有的非参极大似然估计法(NPMLE)和Breslow-Fleming-Harrington估计法(BFH)都对小风险集情形极为敏感，此时生存率会出现急速下降，本文除了提出校正精度的新估计法，同时对现有方法进行比较研究。方法 基于现有NPMLE和BFH，结合Lai-Ying加权思想和条件概率，介绍加权NPMLE和条件NPMLE法，并提出加权BFH法。利用绝对误差积分(IAE)和平均宽度积分(IAW)指标，通过模拟研究比较上述方法的估计精度。结果 模拟结果显示NPMLE、BFH、加权NPMLE、加权BFH和条件NPMLE法的IAE值依次递增，而IAW值显示加权BFH法最小，NPMLE法最大，BFH、条件NPMLE和加权NPMLE法在高低删失率下IAW大小相互逆转。结论 结合模拟结果和实际例子，存在小风险集时推荐使用加权BFH法，其次加权NPMLE法；没有小风险集时5种方法基本一致。

生存分析 左截断 小风险集 非参极大似然估计法 BFH法

在生存数据的临床研究中，生存率的计算是最重要的研究问题之一。常见的生存数据类型有寿终和右删失，另外一种常见的是左截断数据[1]，它指个体的生存时间开始点是在试验随访之前，也就是在随访开始时其已经度过了一段生存期，相当是延迟进入随访研究，一直到发生终点事件或右删失为止，如SARS患者在刚被感染或有初期病症时不会被观察到，而绝大多数是在发烧等病情严重后才进入医院开始随访的，也可以说从感染发病到随访之间有一段延迟的时期。传统Kaplan-Meier(KM)估计法只能处理寿终数据或右删失数据，而忽略左截断信息的存在，此时KM法则会高估生存率，造成分析结果存在偏倚[2]。针对左截断数据的生存率估计，常见的方法有非参极大似然估计法(nonparametric maximum likelihood estimate，NPMLE)[3]，Breslow-Fleming-Harrington估计法(BFH)[4]和迭代Nelson估计法[5]。Gasparini[4]研究发现通常情况下迭代Nelson法比NPMLE法和BFH法更易出现低估生存率情形。在生存时间t较小或者较大时，此时风险集人数可能较少，甚至会出现风险集数和死亡数相等的情况，通常将这种情形称为小风险集，这时NPMLE法估计的生存率会突然出现急速的下降，甚至下降为0，而不管之后是否还有生存者，并且这种不稳定会传播到整个生存曲线[1]，此时BFH法估计的生存率虽然可以保持为正数，表现优于NPMLE法估计值等于0，然而依旧无法避免出现低估生存率的情况[5]，迭代INE法虽然可以较好克服小风险集情形的影响，但在早期依旧会低估生存率，综上所述本文不再讨论迭代INE法。小风险集存在时采用合理恰当的估计方法显得极为重要。针对左截断存在小风险集情形，一种有效且常规的方法是通过估计(t|t>u)的条件分布来计算生存率，其中u是事先定义的恰当时间点，如条件NPMLE法。除此之外，Lai和Ying[6]提出使用加权方法来计算生存率，如加权NPMLE法。加权方法在避免小风险集影响的同时，也无需定义时间点u，避免定义时间点u时主观性带来的影响，对此本文提出新方法加权BFH法，在克服小风险集影响的同时，也无需事先主观性地定义时间点u，更为合理精确地估计生存率。另外，目前为止还没有相关研究对未校正方法和校正方法一起进行模拟比较，只是从理论上加以区别说明，对此本文还会通过模拟研究，综合评价和比较上述5种方法的估计精度，包括新方法加权BFH法，最后进行一个实例分析。

方法介绍

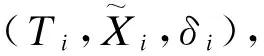
1.非参数极大似然估计法(NPMLE)

(1)

2.加权非参数极大似然估计法(加权NPMLE)

Lai-Ying[6]提出第一种校正方法，称为加权NPMLE法。首先是先选择常数c>0和0<α<1，n代表样本量，则加权NPMLE法定义如下：

(2)

相比于公式(1)，公式(2)设置了权重函数I{Rm(n)(s)≥cnα}，即只有在风险集数Rm(s)大于等于某一设定值cnα时，权重函数设为1，否则设为0，此时加权NPMLE弱收敛于正态分布，有较强的一致性[6]，则可以避免小风险集的影响。

3.条件非参数极大似然估计法(条件NPMLE)

加权NPMLE法(公式(2))使用了加权思路，另一种有效且自然的解决方法是通过估计(t|t>u)条件分布来计算生存率，其中u是事先定义的恰当时间点，则条件NPMLE定义如下：

(3)

此时的条件NPMLE法有较强的一致性[6]。通过选择和改变不同的时间点u，可以获得足够的样本信息和避免出现小风险集情形。

4.Breslow-Fleming-Harrington估计法(BFH)

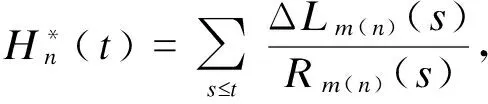
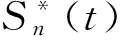
(4)

BFH法虽然在Rm(s)和ΔLm(s)相等的情形下，可以固定保持为正数，表现优于NPMLE等于0，然而依旧无法避免出现低估生存率的情况[5]，也需要进行适当的校正。

5.加权Breslow-Fleming-Harrington估计法(加权BFH)

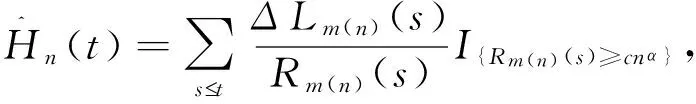
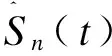
(5)

加权BFH法不论在什么情况下都可以固定保持为正数，并且可以有效避免出现低估生存率的情况。

模拟研究

通过Monte-Carlo模拟比较上述5种方法的表现，主要模拟情形有两种：(1)相同样本量下不同删失率；(2)相同删失率下不同样本量。左截断生存时间T服从威布尔分布，形状参数和尺度参数分别设为4和25；生存时间X分布也服从威布尔分布，参数分别为3和50；研究时间窗口长度为w，则删失时间C=T+w，通过改变w值获得不同删失率；模拟次数设为10000次。主要评价指标[5]有两个：

1.绝对误差积分(integrated absolute error,IAE)

IAE描述的是生存率估计值与生存率真实值的偏倚程度，定义如下：

其中S(t)是指t时刻上10000次模拟后生存率估计值的平均值，W(t)是指t时刻上由概率密度函数求得的生存率真实值。为了避免最后时刻t事件状态的不确定性，设定k=50。

2.平均宽度积分(integrated average width，IAW)IAW是描述的是生存率估计值和生存率真实值的变异程度，定义如下：

其中S95(t)和S05(t)分别指t时刻上10000次模拟后生存率估计值的95%和5%分位数，W(t)是指t时刻上生存率的真实值，同样设定k=50。

(1)相同样本量不同删失率

研究时间窗口长度w分别从5增加到35，对应的平均删失率从0.926减少到0.258。从表1得出，样本量固定时，随着平均删失率的递减，5种估计法的偏倚和变异呈现递减趋势；在偏倚方面，NPMLE法最小，其次是BFH法，加权NPMLE法居中且略微小于加权BFH法，最大的是条件NPMLE法；在变异方面，加权BFH法最小，最大的是NPMLE法，BFH法都大于加权NPMLE法，而在删失率大于0.890时，变异小于条件NPMLE法，小于0.890时，结果相反；同样的在删失率大于0.81时，加权NPMLE法小于条件NPMLE法。

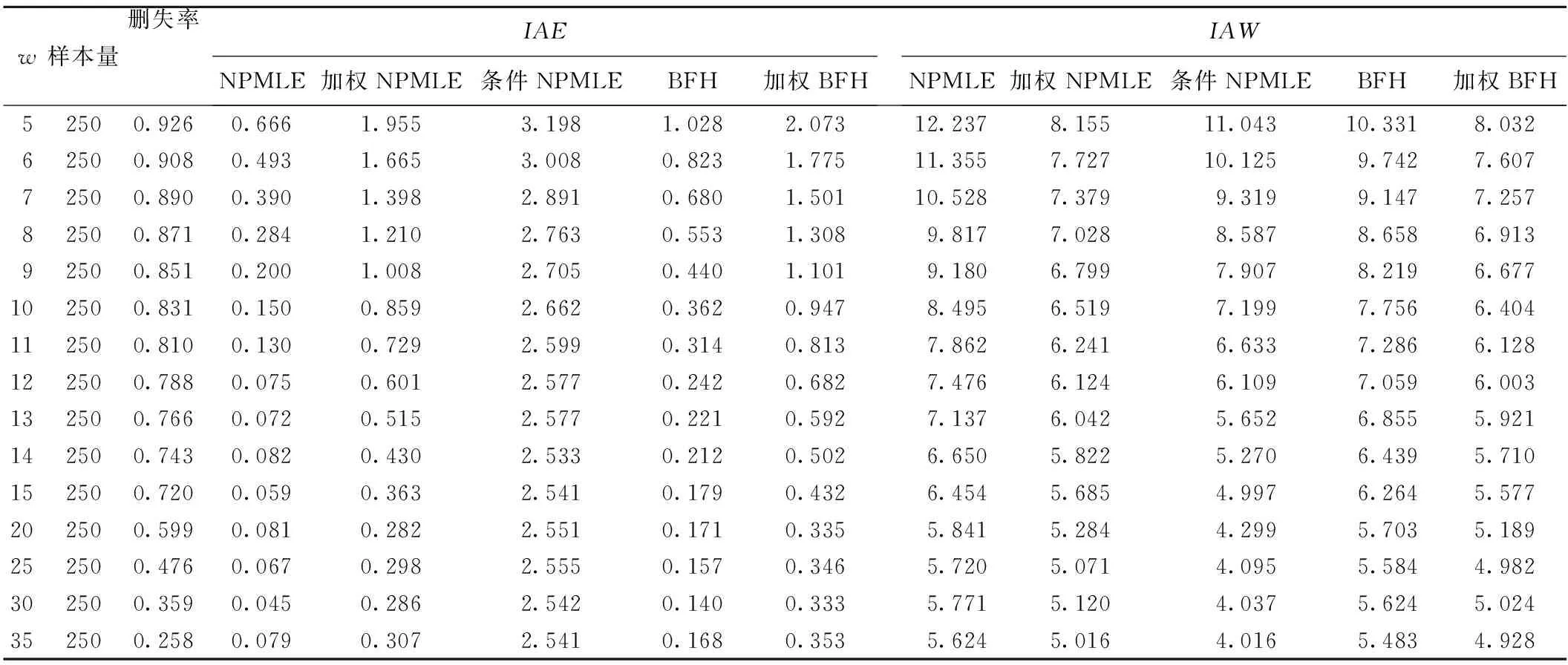
表1 相同样本量不同删失率下5种估计法的偏倚(IAE)和变异(IAW)模拟结果

(2)相同删失率不同样本量

研究时间窗口长度 固定为5，对应的平均删失率固定为0.926。从表2得出，平均删失率固定时，随着样本量从250到2000递减，5种估计法的偏倚和变异都在递减；在偏倚方面，NPMLE法最小，其次是BFH法，加权NPMLE法居中且略微小于加权BFH法，最大的是条件NPMLE法；在变异方面，加权BFH法最小，加权NPMLE次之且略微小于加权BFH法，BFH法居中，然后是条件NPMLE，最大的是NPMLE法。

实例分析

一项关于在加利福尼亚州帕罗奥多的钱宁屋退休中心老年居民寿命的研究[10]，研究对象是从1964年1月到1975年7月期间入住退休中心的老年人，其中男性97例，女性365例，删失率分别为52.6%和64.4%。每个个体必须生存到足够年纪65岁(780个月)才能进入在退休中心，则生存时间是死亡时间，左截断时间是进入研究时间，删失时间是研究截止时间或者对象退出研究时间。图1显示的是男性老年人生存率，发现黑色点线NPMLE法在800个月之前急速下降为0，灰色点线BFH虽然避免降低为0，但依旧有突然下降的趋势；令c=1,α=1/3，使得权重函数I{Rm(n)(s)≥cnα}中cnα男性和女性分别约为5和8，合理地避免风险集数Rm(s)过小情形，如男性Rm(800)为1，加权BFH和加权NPMLE两条实线基本重合；点虚线条件NPMLE(t>781个月)和两条实线都基本重合，三种方法都避免了生存率突然降低为0的情况。图2是女性老年人的生存率，发现当不存在风险集数Rm(s)过小或Rm(s)和死亡数ΔLm(s)相等的小风险集情形，校正与未校正的估计法结果基本一致，5条图线基本重合在一块。

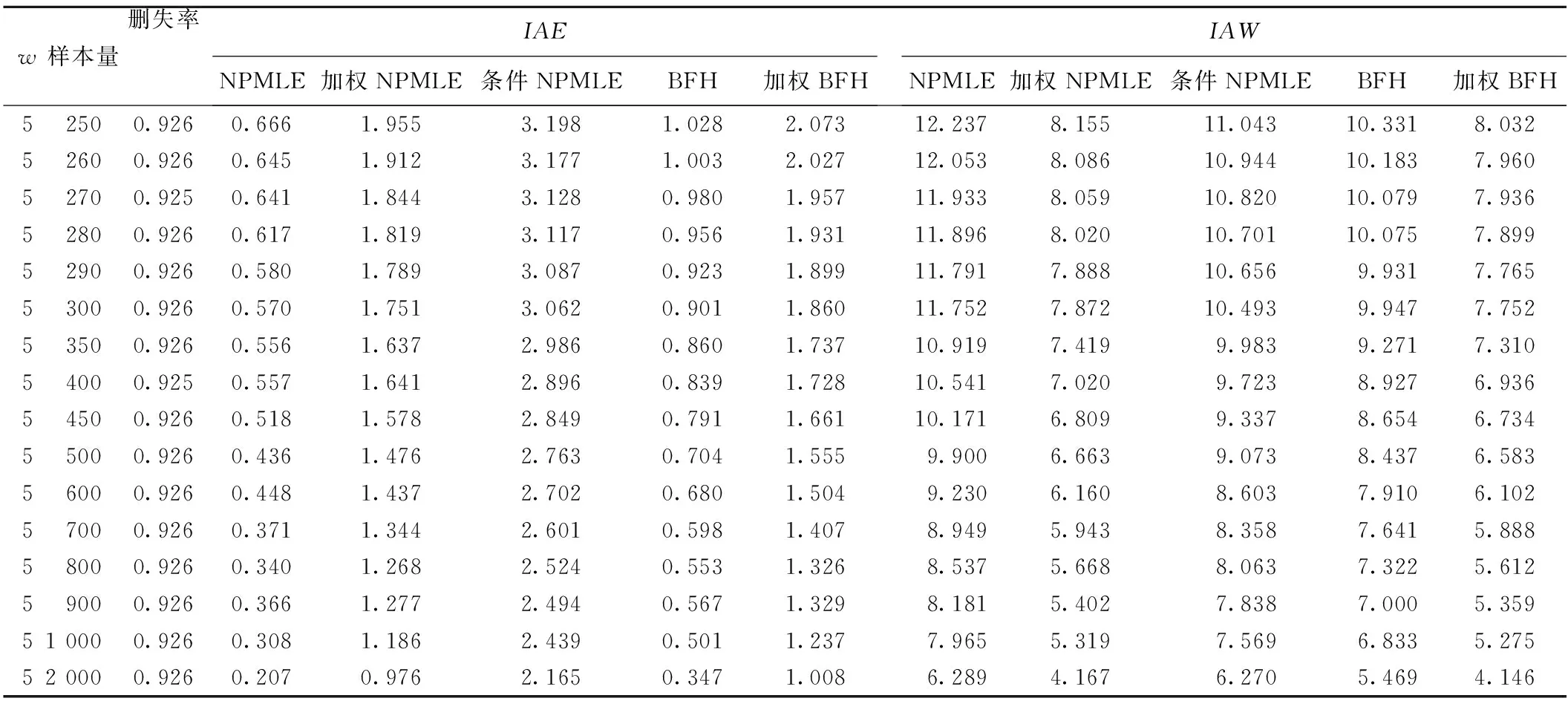
表2 相同删失率不同样本量下5种估计法的偏倚(IAE)和变异(IAW)模拟结果

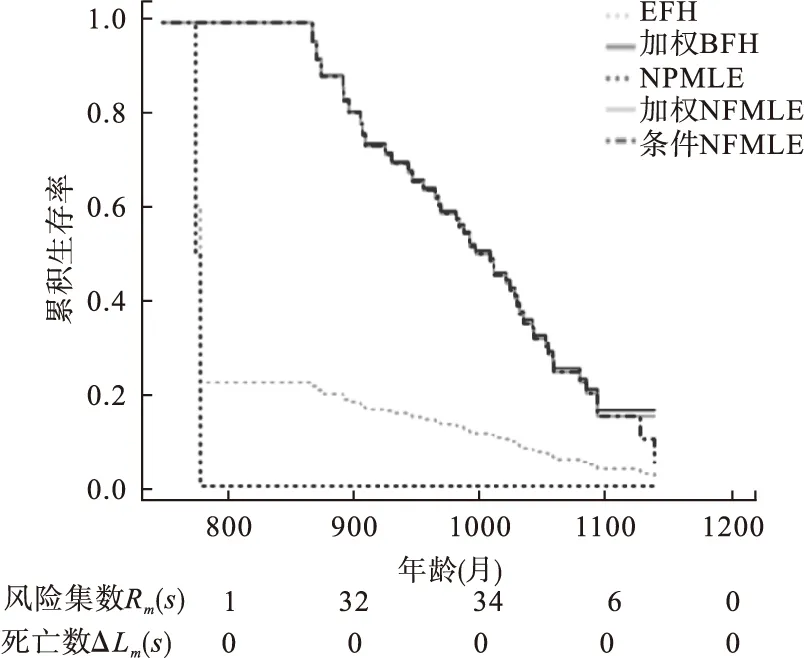
图1 男性老年人的累积生存率图

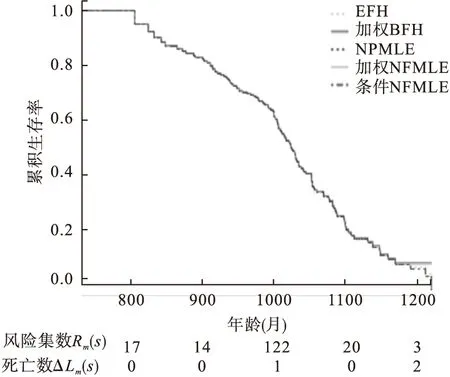
图2 女性老年人的累积生存率图

讨 论

在医学临床研究中，左截断类型数据是常见的类型之一，并且其生存率的计算是最重要的研究问题之一。关于左截断类型生存率的计算过程，常常出现风险集数Rm(s)过小或风险集数Rm(s)和死亡数ΔLm(s)相等的小风险集情形，导致生存率突然出现急速下降甚至下降为0的异常情况，有效的解决策略是采用加权思想和条件分布思想，本文相应的提出了加权BFH法。进行模拟分析，从偏倚程度和变异程度两方面综合评价NPMLE法、加权NPMLE法、条件NPMLE法、BFH法和加权BFH法共5种估计法的表现，根据模拟结果，可以发现NPMLE法有最小的偏倚，同时有着最大变异，说明NPMLE法存在不稳定性；条件NPMLE同时具有较大的偏倚和变异，可能是因为模拟研究中条件t>u，其中u取时间25%分位数点，选择时间点偏后导致的，u的选择具有一定的主观性；加权NPMLE法在低删失率下比条件NPMLE法有着更高的变异程度；BFH法有较小的偏倚但有较大的变异，表现略优于NPMLE法，5种方法只有加权BFH法基本维持较低且合理的范围内，虽然加权方法中常数c和α都具有一定的主观性，模拟结果显示依旧可以很大程度地避免偏倚和变异的产生，最接近真实的生存率值。在左截断类型数据的实际应用中，应注意是否有小风险集情形的出现，对应地采用合理的方法，避免做出错误的结论。

[1]Klein JP,Moeschberger ML.Survival Analysis:Techniques for Censored and TruncatedData.Second Edition.New York:Springer,2003.

[2]Nahman NS,Middendorf DF,Bay WH,et al.Modification of the Percutaneous Approach to Peritoneal Dialysis Catheter Placement UnderPeritoneoscopic Visualization:Clinical Rensults in 78 Patients.Journal of the American Society of Nephrology,1997,1992(3):103-107.

[3]Lynden BD.A method of allowing for known observational selection in small samples applied to 3CR quasars.Monthly Notices of the Royal Astronomical Society,1971,115(1):95-118.

[4]Gasparini M,Gandini M.A comparison of nonparametric estimators of survival under left-truncation and right-censoring motivated by a case study.Statistica,2011,71(3):391-406.

[5]Pan W,ChappellR.A Nonparametric Estimator of Survival Functions for Arbitrarily Truncated and Censored Data.Lifetime Data Analysis,1998,4(2):187-202.

[6]Lai TL,Ying Z.Estimating a distribution function with truncated and censored data.The Annals of Statistics,1991,19(1):417-422.

[7]Woodroofe M.Estimating a distribution function with truncated data.The Annals of Statistics,1985,13(1):163-177.

[8]Wang MC,Jewell NP,Tsai WY.Asympotic properties of the product limit estimate under random truncation.The Annals of Statistics,1986,14(4):1597-1605.

[9]Lai TL,Ying Z.Linear rank statistics in regression analysis with censored or truncated data.Technical Report,Department of Statistics,Stanford University,NO.2,March 1988.

[10]Hyde J.Testing survival under right censoring and left truncation.Biometrika,1977,64(2):225-230.

(责任编辑：郭海强)

The Study of Nonparametric Estimate Method for Left Truncated and Right Censored Data

Chen Jinbao,Hou Yawen,Chen Zheng

(DepartmentofBiostatistics,SchoolofPublicHealth,SouthernMedicalUniversity(510515),Guangzhou)

Objective Nonparametric maximum likelihood estimate(NPMLE)and Breslow-Fleming-Harrington estimate(BFH)are extremely sensitive to small risk set for left truncated and right censored data,this study aims to develop estimation methods to improve the estimation accuracy and compare the existing methods.Methods We introduced the NPMLE,weighted NPMLE,conditional NPMLE,BFH and a new weighted BFH estimate.Simulation studies were carried out to compare five methods via the integrated absolute error(IAE) and integrated average width(IAW).Results The IAE of NPMLE,BFH,weighted NPMLE,weighted BFH and conditional NPMLE is ascending in turn;The IAW of weighted BFH is the lowest and NPMLE is the largest,BFH,conditional NPMLE and weighted NPMLE is reversed under different censored rate.Conclusion According to the results of simulation and example,weighted BFH and weighted NPMLE is recommended in turn when the risk set is small.Otherwise,the results of five methods would be consistent.

Survival analysis;Left truncation;Small risk set;Nonparametric maximum likelihood estimate(NPMLE);Breslow-Fleming-Harrington estimate(BFH)

国家自然科学基金(81673268,81202288)，广州市科技计划项目(2012J5100023)，南方医科大学科研启蒙计划(B1012444)

1.南方医科大学公共卫生学院生物统计学系(510515)

2.暨南大学经济学院统计学系

△通信作者：陈征，E-mail:zchen@smu.edu.cn