基于LFM算法的改进社区发现算法

肖永嘉，朱征宇

（重庆大学计算机学院，重庆 400000）

基于LFM算法的改进社区发现算法

肖永嘉，朱征宇

（重庆大学计算机学院，重庆 400000）

由于能够反映网络内部结构，重叠社区划分在各领域有着越来越重要的作用。LFM算法是其中较为流行的一种社区划分方法。但其存在一些缺点，例如在网络变得庞大和复杂的时候，时间消耗会变得巨大。为了解决这一问题，提出核心区域的概念，并藉此对LMF算法进行改进。最后通过实验验证，发现该算法能够减小时间消耗，同时能够得到更为可靠的社区划分。

重叠社区划分；LFM；核心区域

0 引言

现实世界的很多复杂的相互作用的系统往往被抽象成网络来表示，用来让人们更好地理解复杂系统的全部特性，更好地应对现实的变化。例如互联网环境下的社交网络、电子商务；流行病传播学中的疾病预防控制过程，生物学网络中蛋白质组织构造等。随着人们对复杂网络的研究日益深入，社区结构作为复杂网络存在的普遍特征，由于能有效地揭示网络系统中群体的共性规律，是解决复杂系统的基础，又能推进相关应用的发展，已经成为网络研究的一个重要分支。而重叠社区的发现可以更为准确地理解网络内部的拓扑结构信息，在近些年的研究中得到了越来越多的关注。

1 相关工作

社区并没有一个严格意义上的定义，较为广泛接受的是Newman和Gievan提出的“同一社区内的点与点之间的链接更紧密，不同社区之间的点的链接更稀疏[1，2]。”重叠社区即与其他社区拥有重叠节点的社区。如图1中G1，G2拥有重叠的节点A1，A2因此G1，G2都是重叠社区。

基于局部优化的社区发现方法可以分为四类：局部拓展优化方法，从给定的初始节点逐步合并引起最大的社区度量增量的近邻节点，从而进行局部扩展优化，各方法的主要差异在于对局部社区的度量不同。例如子图度量优化的局部社区扩展算法LWP[3]，L-壳扩展的社区发现算法，LMD算法[4]，LFM算法[5]等；派系过滤方法CPM[6，12]其定义了一种严格的社区结构，并允许社区间存在重叠。为进一步分析网络社区的重叠特性基于子图强度将CPM算法扩展到加权网络，提出了一种加权派系过滤算法CPMw[7]，为了进一步有效应用到大规模的加权和非加权社交网络提出了一种快速派系过滤算法SCP标签传播法（LPA）[8]基于单个标签传播，网络中的每个节点被确定地划分至单一社区中，忽略了社区结构的重叠特性，为此拓展出多标签传播算法copra[9]；以及局部边聚类优化方法，菲利波·拉迪奇（Filippo Radicchi）等人定义了一种边聚类系数，并提出了一种社区发现的局部方法[10]，Ahn等人提出了一种基于连边局部相似性的边社区发现方法来检测社区的重叠性和层次性[11]，潘磊等人提出另一种局部的边社区发现方法等。

本文的主要工作是针对LFM算法在时间复杂度上的明显不足进行改进，得到了较原算法在时间，评价效果都更为出色的改进算法。

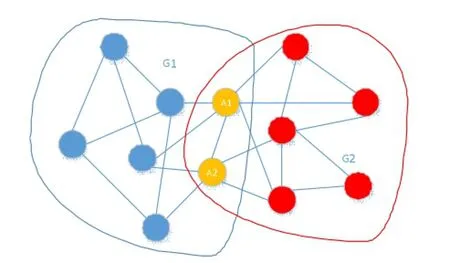
图1

2 算法介绍

2.1 相关定义

网络可以通过抽象成图G=（V，E）来表示，其中V= {v1，v2，v3，…}表示节点的集合，E={e1，e2，e3，…}表示边的集合。

LFM算法中的适应度fG的定义如下：

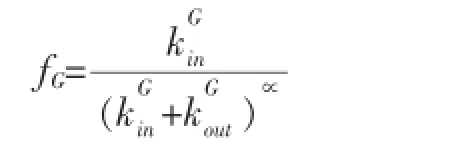
其中kGin和kGout分别指的是图G中内部和外部度数的总和，∝是一个正实数参数用来控制社区的规模。较大的∝值会产生较小的社区，较小的∝值会导致社区较大。此外原算法的作者对∝的取值进行了分析：在多数情况下当∝<0.5时整个网络被划分为一个社区，当∝>2时，每个节点都是一个单独的社区。同时对本文实验包含的三个测试集上时的实验表明：∝取值为0.9时效果最好。

适应度函数的定义如下：

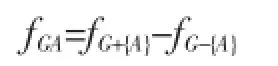
其中G+{A}表示G中包含A的子图，G-{A}则表示G中不包含A的子图。如果fGA>0则表明将节点A加入社区G有益于提高社区质量，则将节点A加入社区G。

2.2 LFM算法的思想

首先引入包含顶点A的自然社区的获取过程：

假设已有一个包含节点A的子图G，

①对G的所有邻接点循环操作，计算每个邻接点对G的适应度函数值；

②将适应度值最大的点加入子图G形成更大的子图G'；

③重新计算子图G'中的所有点的适应度值；

④如果其中一个节点的适应度值变为负数，则将该节点从子图G'中剔除，形成新的子图G"；

⑤如果发生④，则从③开始重复，否则，以子图G"从①开始重复，直到第①步中所有邻接点对子图G的适应度值都为负数时结束。

对于LFM算法的执行过程就可以概括为以下几步：

①随机选取一个节点A；

②探测获取包含节点A的自然社区；

③随机选取一个为被划分至任意社区的节点B；

④探测获取包含节点B的自然社区，不管其临节点是否属于其他社区；

⑤从③开始重复，直至所有的节点都被至少分配在一个社区。

算法存在的问题有：

①在获取自然社区时会有节点反复加入社区然后被剔除的死循环现象；

②在获取自然社区时每加入一个新的节点都要重新计算一下社区内所有节点针对该社区的适应度值，导致计算量巨大。

针对上述两条缺点，我们采取如下措施：

①在自然社区发现过程中，对现有社区G的所有邻接点进行区别标记，如果某个邻接点曾被加入临时社区则在自然社区的获取过程中不再将其加入临时社区。

②引入核心区域的概念，并规定在获取自然社区的过程中，如果节点A属于现有社区的核心区域则则认为该节点将确定属于现有社区，不再计算其适应度值。

这样就解决了原算法中出现的问题，极大地提高了算法速度和划分社区的质量。

2.3 改进算法思想

我们定义：如果某一个节点A在只跟当前社区G内的节点有边相连，则该节点属于当前社区的核心区域。如上图2所示。

根据适应度值的定义：

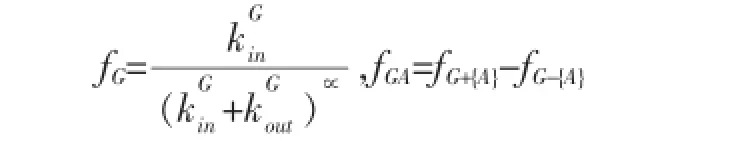
我们可以得到表达式：

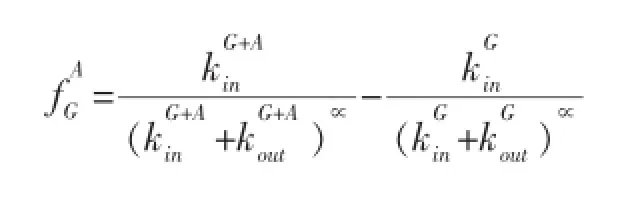
因此我们给出结论如果节点A属于临时社区G的核心区域，则将节点A加入社区G有益于社区划分质量的提高。

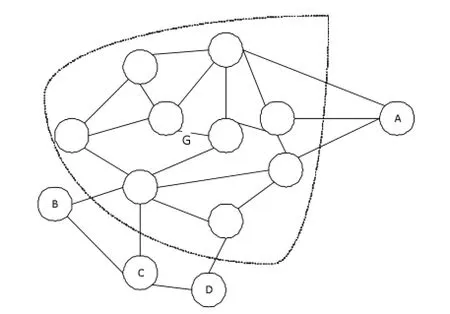
图2

此外，我们对临时社区的所有邻接点增加一个标记位，用来表示该邻接点是否被访问过即计算过其对社区G的适应度值，在拓展过程中，如果邻接点中出现了已被访问过的节点，则说明该节点在临时社区G’重新计算适应度值的过程中不再有益于提高社区划分质量，我们认为该节点将永远不利于提高社区划分质量。因此我们在新形成的社区G”的拓展过程中将跳过该节点，不再重复计算其对社区的适应度值。

改进后的包含节点A的自然社区获取过程如下：

假设已有一个包含节点A的子图G，

①对G的所有邻接点进行判断，如果属于当前社区的核心区域，则对其标记并直接加入当前社区，如果不是进入②；

②对G的非核心区域且未访问过的邻接点循环操作，计算每个邻接点对G的适应度函数值；

③将适应度值最大的点加入子图G形成子图G'，并将其标记为已访问;

④重新计算子图G'中的所有非核心区域的点的适应度值；

⑤如果其中一个节点的适应度值变为负数，则将该节点从子图G'中剔除，并将其标记为已访问过，形成新的子图G"；

⑥如果发生⑤，则从②开始重复，否则，以子图G"从①开始重复。

直到所有邻接点对子图G的适应度值都为负数时结束。

3 实验

本章通过实验验证我们提出的改进算法的性能，我们将其与LFM原算法以及其他几种较有代表性的算法进行比较，分别是CPM，COPRA。其中为了使这两个算法效果最佳，在CPM算法中我们选取k取值为3，COPRA算法中v的取值为3。而在LFM算法及我们的改进算法中，我们参考LFM作者的分析取效果最佳的0.9。

3.1 实验环境

处理器Intel core i5-5200U 2.20GHz，内存4G，硬盘500G，系统为Windows7 x64，编程语言为Java，开发环境为Eclipse4.4。

3.2 实验数据

实验数据包括真实网络数据集和人工合成网络数据集两大类。

五组真实网络数据集的参数如下，其中karate网络为W.W.Zachary描述的20世纪70年代一所美国大学的空手道俱乐部中34名成员之间的友谊关系图，dolphin网络为David Lusseau描述的新西兰神奇峡湾一个拥有62只海豚族群的关系网络，American football网络为Girvan等人描述的2000年秋季常规赛IA级别的115只球队比赛的关系网络，email网络为具有1133个节点和5451条边的网络，blogs网络为Adamic和Glance在2005年记录的关于美国政治的3982个博客之间超链接的有向网络。

表1 真实网络数据集

人工合成网络数据集的生成我们采用LFR（Lancichinetti-Fortunato-Radicchi）基准程序来构造人工网络。根据Santo Fortunat在个人网站上提供的源程序，运行时的需要按如下格式输入参数：benchmark-N-kmaxk-maxc-on-mu-om。

其中N表示节点数目，k表示网络中节点的平均度；kmax表示节点的最大度；minc表示最小社区包含的节点的个数；maxc表示最大社区包含的节点的个数；on表示重叠节点的个数，om表示每个重叠节点属于几个社区；mu表示用来表示社区的混乱程度，mu越大社区发现的难度越大。

3.3 评价指标Qov和NM I

对于真实网络，我们使用模块度Qov对社区的划分质量进行判断，模块度的提出基于一个简单地理念：如果一个子图是社区那么它的内部节点之间的连边数一定比随机生成的自图的内部节点的连变数多。模块度的相关概念可以参考文章，这里只给出公式。

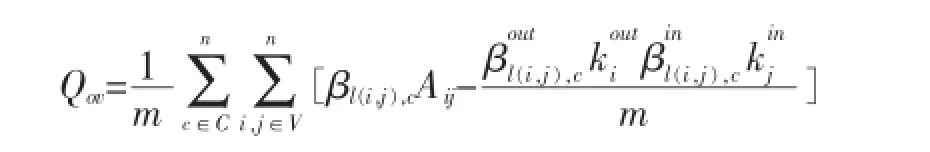
对于由LFR基准程序生成的人工合成网络，在生成网络的同时程序会给出参考社区划分，因此我们用标准化互信息度NMI（Normalized Mutual Information）来评价各种算法得到的社区划分与已知社区划分的相似程度。如果NMI=1则表示算法得到的结果与已知的社区划分完全一致。

3.4 人工合成网络上的时间对比

为了验证我们的改进算法与原算法在时间上的改进，我们使用LFR基准程序生成两组人工合成网络节点数目分别从1000-10000，10000-100000.为了降低整个实验过程的总耗时，我们将mu置为0.1。

其他参数取值分别为k=10，maxk=50，minc=10，maxc=50，on=100，om=0.1。

图3

可以看到我们的改进算法在网络规模相对较小（节点数<10000）时与原算法相比具有显著提升，随着网络节点数目的增加我们的算法与原算法在时间消耗上的差距相对变小，主要原因是网络规模的剧增导致社区的邻接点数目剧增。导致在标记邻接点和判断是否为核心区域时消耗大量的时间。

3.5 现实网络效果Qov对比

可以看到我们的改进算法在Karate，football，email三个网络中效果优于原算法，在dolphins网络中持平，在blogs网络中效果比原算法差；与CPM算法相比我们的改进算法在Karate，football和blogs网络中效果较好，在dolphins和email网络中效果较差；与Copra算法相比，我们的改进算法在karate，email和blogs网络中效果较好，在dolphins和football网络中效果较差。

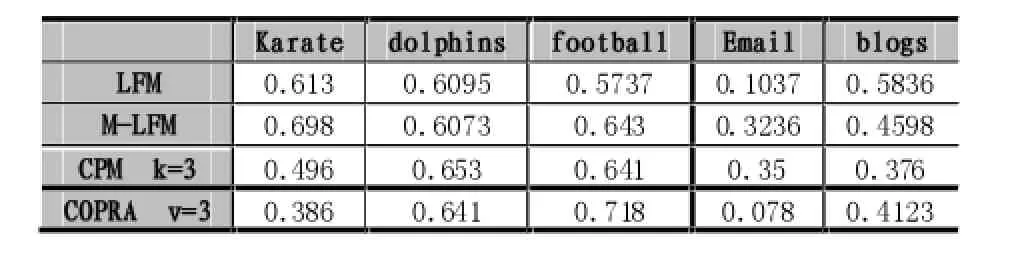
表2

3.6 人工合成网络效果对比

为了比较各算法在不同类型网络下的社区发现质量，我们根据网络规模N及每个重叠节点所属的社区个数om的不同，生成了四组由大小网络和大小社区组合而成具有不同特征的人工网络。为了降低计算复杂度，我们将影响社区复杂程度的参数mu固定为0.1。其他参数如下图所示。

得到的各组数据分别如下所示：

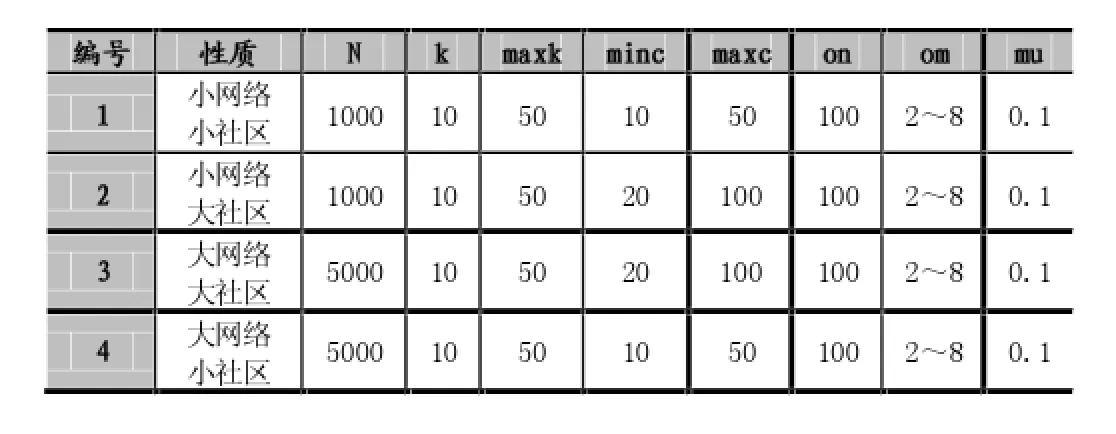
表3

我们可以看到在网络规模较小的情况下（第1，2组数据），我们的改进算法的社区划分质量高于其他三种算法；在网络规模较大，同时社区规模较大的情况下的情况下（第3组数据）我们的改进算法的社区划分质量也高于其他三种算法；只有在网络规模较大且社区规模较小的情况下，我们的改进算法的社区划分质量逊色于CPM算法，但仍然高于原算法和COPRA算法。

4 结语

本文针对LFM算法的不足提出了相对应的改进方案，结果表明在时间和社区划分质量上相较于原算法都有了显著地提升。但是无论原算法还是我们的改进算法都存在社区划分不稳定的缺点，如何提高其稳定性有待进一步的工作。

[1]M.E.J.Newman And M.Girvan.Finding and Evaluating Community Structure In Networks.Physical Review E，69:026113，2004.

[2]V.Nicosia，G.Mangioni，V.Carchiolo and M.Malgeri.Extending the Definition Of Modularity To Directed Graphs With Overlapping Communities，Arxiv:0801.1647v4[Physics.Data-an]24 Mar 2009

[3]Luo F，Wang JZ，Promislow E.Exploring Local Community Structures In Large Networks.Web Intelligence and Agent System，2008，6（4）:387-400.

[4]Chen Q，Wu T T，Fang M.Detecting Local Community Structures In Complex Networks Based on Local Degree Central Nodes.Physica A-statistical Mechanics And Its Applications,2013,392(3):529-37.

[5]Lancichinetti A,Fortunato S,KertéSz J.Detecting The Overlapping and Hierarchical Ommunity Structure in Complex Networks.New Journal of Physics,2009,11（3）：033015.

[6]Palla G,Derenyi I,Farkas IEt Al.Uncovering the Overlapping Community Structure of Complex Networks in Nature And Society. Nature,2005,435（7043）：814-8.

[7]Farkas I,Bel D,Palla G Et A l.Weighted Network Modules.New Journal Of Physics,2007,9（6）：180.

[8]Raghavan U N,Albert R,Kumara S.Near Linear Time Algorithm to Detect Community Structures in Large-Scale Networks.Physical Review E,Statistical,Nonlinear,and SoftMatter Physics,2007,76（3 Pt2）：036106.

[9]Gregory S.Finding Overlapping Communities In Networks By Label Propagation.New Journal of Physics,2010,12（10）：103018.

[10]Radicchi F,Castellano C,Cecconi F Et Al.Defining and Identifying Communities in Networks.Proceedings of the National Academy of Sciences of the United States of America,2004,101（9）：2658-2663.

[11]Symeon Papadopoulos As,Athena Vakali,Yiannis Kompatsiaris Et Al.Bridge Bounding:a Local Approach for Efficient Community Discovery In Complex Networks.Physics And Society,2009.

[12]DeréNyi I,Palla G,Vicsek T.Clique Percolation In Random Networks.Physical Review Letters,2005,94（16）：160202.

Im proved Algorithm of Overlapping Community Detection Based on LFM

XIAO Yong-jia，ZHU Zheng-yu

（College of Computer Science,Chongqing University，Chongqing 400000）

Overlapping community detection has becomemore and more important since it can reveals the inner structure of networks.LFM algorithm is one of themost popular way to detect communities in complex networks,however the algorithm itself has some weaknesses,such as large time consumption when the network become large and complex.To overcome these problems,based on LFM,presents an improved LFM algorithm(M-LFM)which proposes a definition of core area and apply it into the process of community detection with LFM. Experiments on real networks and artificial networks show that the improved algorithm can decrease time consumption and get better result than LFM.

肖永嘉（1991-），男，山东临沂人，研究方向为复杂网络中重叠社区发现算法研究

2017-03-15

2017-05-10

1007-1423（2017）14-0021-06

10.3969/j.issn.1007-1423.2017.14.004

朱征宇（1959-），男，安徽马鞍山人，博士生导师，研究生方向为数据挖掘技术、互联网技术与检索方法、电子商务网站与应用、软件工程方法与应用、智能交通

Overlapping Community Detection;LFM;Core Area