基于连续小波阈值去噪算法的目标检测研究

刘冰，刘雪梅

（1.达州职业技术学院，达州 635001；2.西南大学计算机与信息科学学院，重庆 400715；3.四川省达州市统计局，达州 635000）

基于连续小波阈值去噪算法的目标检测研究

刘冰1，2，刘雪梅3

（1.达州职业技术学院，达州 635001；2.西南大学计算机与信息科学学院，重庆 400715；3.四川省达州市统计局，达州 635000）

对含噪图像的去噪处理是目标检测任务中的一个经常性工作，由于传统软/硬阈值去噪算法其估计小波系数在所设定的阈值处存在不连续和不可导的缺陷，常常导致重构图像的质量达不到目标检测的要求。对传统软/硬阈值去噪算法存在的问题进行详细的分析，并据此重新构造一个在所设定的阈值处具有连续可导的阈值函数，同时还给出相应的算法步骤。仿真实验表明，运用所提出的算法能够很好去除含噪图像中的噪声，较之传统软/硬阈值算法效果更加明显，其处理后的图像能很好地满足更进一步的目标检测任务的要求。

图像去噪；软/硬阈值去噪；连续小波阈值；均方误差；峰值信噪比

0 引言

随着机器学习理论和特征分析技术的发展，视觉任务的前提性工程——目标检测一直是最具挑战性的研究课题。由于受环境及设备本身因素的影响，被检测目标及其背景往往都带有某种噪声。因此，对含噪图像进行去噪处理就成为了在目标检测任务中非常重要的一环，其处理结果将直接影响到能否从含噪图像中最终检测得出目标。当前，对图像进行去噪的主要方法大致有两类：一类是空间域方法，另一类是频率域方法[1-4]。前者是对图像像素进行处理，通常先是通过选取某一图像平滑模板对原始图像作卷积运算，然后经过对原始图像中的噪声进行压抑或消除，达到图像去噪的目的，但在处理的过程中，没有顾及到图像中每一像素的特点，常常导致去噪后的图像的边缘细节变得模糊不清，效果较差；后者则是先对原始图像进行某种变换，接着对变换后的图像进行滤波处理，最后通过重构来得到去噪后的图像，较前者而言，处理后的图像质量较高。

由于小波变换在分离相关性较强的数据方面具有独特的优势，在近年来，它也成为频率域方法中最受青睐的一种去噪处理方法[5-11]。由于在运用其他频率域方法进行噪处理的实践中，通常在滤波处理阶段采用低通滤波器直接滤除高频信息的方法来实现，而阈值的设定又较为固定，这常常导致一些有用的高频的信息随着噪声的去除而丢失，从而影响到图像去噪效果。而小波变换具有独特的多分辨特性，通过运用不同中心频率的带通滤波器对信号进行滤波，就能够把主要反映噪声频率的小波系数去掉，达到图像去噪的目的[12-13]。目前，在众多的基于小波变换的去噪算法中，最为成熟和使用得较多的方法是阈值去噪法，其中，Donoho提出的软/硬阈值去噪法[14-16]影响最大。阈值图像去噪算法的关键是构造阈值函数，其中阈值的设计是又是最为关键的方面。由于硬阈值法的估计小波系数在所设定的阈值处不具有连续性，从而造成重构信号的振荡；虽然软阈值法有效地克服了这一缺陷，但在所设定的阈值处不具有可导性，这又限制了其更进一步的运算，不利于实际的应用。基于软/硬阈值去噪法存在的问题，本文通过构造一个新的阈值函数并结合运用小波系数域处理及阈值估计技术提出了一个基于连续的小波阈值图像去噪处理算法。实验表明，运用该算法进行目标检测，能获得较为清晰的目标图像，同时运算速度也较为理想。

1 传统小波阈值去噪

1.1 算法原理及实现步骤

传统的小波阈值去噪算法的原理在于：由于含有噪声的图像在经过多层小波变换后，所得到的一系列小波系数中，通常较大的值代表原始图像信息，较小的值代表噪声信号。这样，在对这些系数进行进一步的处理过程中，就可以通过设定一个阈值来分离这些系数，将那那些值相对较小的系数去除，保留那些值相对较大的系数，最后通过对保留下来的系数进行重构来获得去噪图像。在实际应用中，通常的实现步骤如下：

第一步，选择适当的小波基函数并确定小波分解的层数，计算出含噪图像的小波分解系数；

第二步，对每层的小波系数选择一个恰当的阈值，仅对高频系数进行处理，得到小波估计系数；

第三步，对得到的小波估计系数进行小波重构，得到去噪后的原始图像。

1.2 软/硬阈值算法

假设含有噪声的图像用f（i，j）表示，原始图像用s（i，j）表示，噪声用n（i，j）表示，则它们的数学模型可表示为：

对f（i，j）进行多层小波变换，设第n层、第m个小波系数为W（n，m），则传统的硬阈值去噪法的数学模型可用（2）式表示，软阈值去噪算法的数学模型可用（3）式表示：

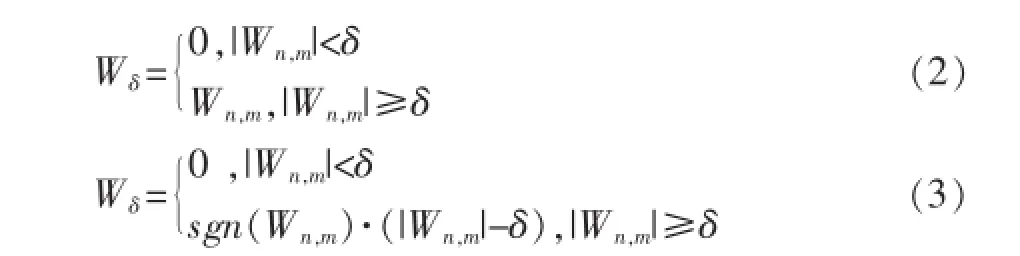
在（2）、（3）式中，Wδ为阈值处理后的估计小波系数，sgn（·）为符号函数，δ为第n层小波变换的阈值。

阈值法处理的关键在于阈值δ的选择，如果选择太小，代表噪声的小波系数不能去除完全；如果太大，代表图像的小波系数将被过滤掉，导致还原图像的失真。在实际应用中，（2）、（3）式中δ值的选取通常用如下的经验公式获得：

在公式（4）中，φ为噪声的强度，L为图像的长、宽像素数的乘积。

运用上述两种方法对图像进行去噪处理，虽然能取得一定的效果，但是不太理想。分析原因，主要在于：无论δ如何选取，公式（2）在该处都不连续，这就使得利用Wδ获得的重构信号存在附加的振荡，导致最后的还原信号失去光滑性；虽然公式（3）在阈值处的连续性相对较好，但当|Wn，m|=δ时，Wδ与W之间总存在偏差，同时Wδ的一阶导数也不连续，因此影响了实际的去噪效果[17-18]。

2 连续小波阈值算法

2.1 阈值函数的构造

为了能有效地解决软/硬阈值去噪法存在的问题，本文构造了一个新的阈值函数：

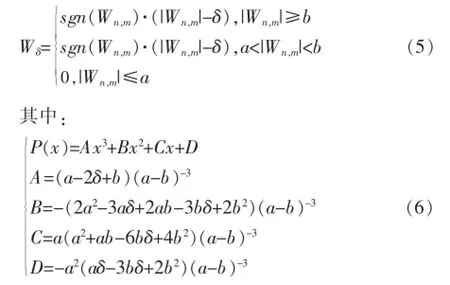
下图描述了式（5）中处理后的小波系数Wδ和原小波系数Wn，m之间的关系：

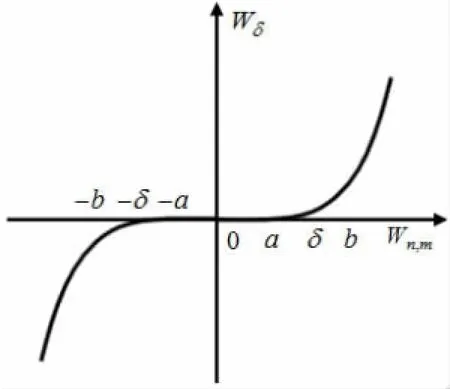
图1 新阈值函数图

从（5）式和图1容易看出，Wδ在a，b处连续且一阶可导。与传统的软/硬阈值去噪法相比，不仅具有整体的连续性，而且阈值δ的调节也非常灵活。

2.2 算法步骤

根据上节构造的阈值函数，设计如下的算法步骤：

第1步：选择适合于具体含噪图像特点的小波基函数。通过对含噪图像f（i，j）进行多层的小波变换，得到一系列小波分解系数Wn，m。（其中：Wn，1∈{LHn}，Wn，2∈{HLn}，Wn，3∈{HHn}，Wn，1、Wn，2、Wn，3分别代表水平方向，垂直方向和对角线方向的小波系数，n=1，2，…，l，l代表分解的层数）。

第2步：根据文献[19]的结论（η=median（|W1，3|/c），c=0.6745）求出式（1）中噪声n（i，j）的方差η值，并根据式（2）求出δ。

第3步：以第2步的δ值作为阈值，根据式（7）分别对LHn，HLn，HHn进行处理，得到小波系数的估计值Wδ。

第4步：利用小波基函数将第3步得到的Wδ和代表低频部分的小波系数进行重构，重构的结果即是去噪后的图像s（i，j）。

3 算法测试与评价

为了验证本文提出方法的有效性，从国际通用测试图库中选取Lena图像并添加高斯白噪声，然后用软/硬阈值法及本文中提出的算法在MATLAB软件[20]上进行处理。实验中，选择COIF4作为小波基函数[21]并对加噪图像进行4层小波分解。结果表明，本文提出的算法较软/硬阈值法的去噪效果更好。其定性测试结果如图2所示。

图2 Lena图像的测试去噪比较效果

另外，在定量测试中，我们采用均方误差（MSE）和峰值信噪比（PSNR）两个指标进行对比[22]。一般来说，一幅高质量的图像PSNR的值很大，而MSE的值很小。下面是MSE和PSNR的数学模型：

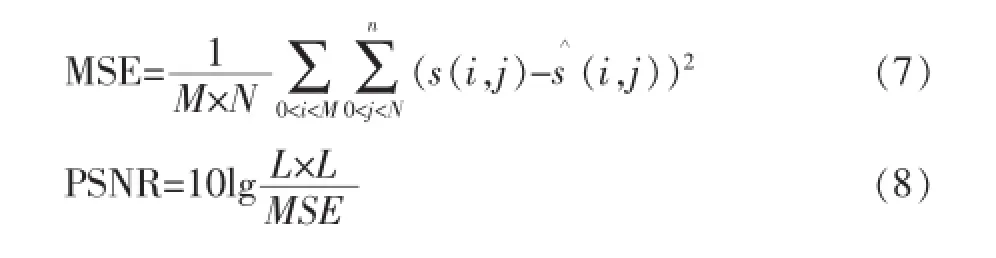
其中，式（7）中的M×N表示图像的大小，s（i，j）表示无噪图像，s∧（i，j）表示去噪后的图像。式（8）中的L表示图像的最大灰度值，通常取255。

实验结果表明：本文算法比起传统的软/硬阈值法所获得的去噪图像的均方误差值更小，而峰值信噪比则更大一些。具体测试结果如下表所示。

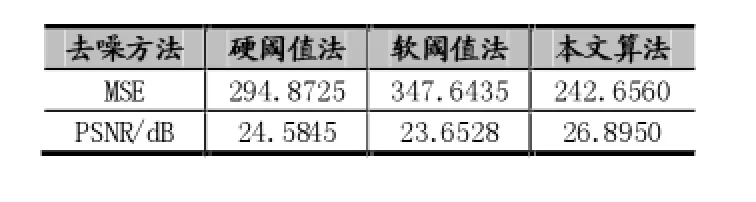
表1 Lena图像去噪后MSE和PSNR对比情况表

4 实验分析

为了验证本文提出的算法在目标检测中的实际应用效果，实验中对某远程视频图像中的行人目标进行分析检测。该输入数据为某小区外的一段远程视频，其视频帧大小为684×528，如图3（a）、（b）所示。

图3 某小区外远程视频帧图像

从图3中不难看出，行人目标在背景图中所占比例较小，同时背景图噪声较多，要对该目标进行准确检测，存在相当大的难度。图4（a）、（b）是运用传统的软/硬阈值去噪法中较好的软阈值法得到两幅帧图像，显然无法检测出行人的目标。图4（c）、（d）是运用本文新构造的阈值函数所设计的算法得到的两幅帧图像，不难看出：背景中的对目标行人所造成的干扰被有效地过滤掉了，准确检测出了该目标。由此说明本文的改进方法的具有较强的有效性。

图4 某远程目标（行人）检测效果对比图

5 结语

在通常的目标检测任务中，极其重要的一环是对含噪图像的处理。由于传统的软/硬阈值算法在图像去噪处理中存在固有的缺陷，即硬阈值算法所设定的阈值不能使图像处理后的估计小波系数连续，软阈值算法所设定的阈值虽然能使图像处理后的估计小波系数连续，但在所设定的阈值处又不可导，这样就会使得在图像去噪处理过程中其重构信号要么存在附加的振荡，导致最后的还原信号失去光滑性；要么在设定的阈值处重构信号与原始信号之间存在偏差，引起还原图像失真。针对这一问题，本文在传统的软/硬阈值算法的基础上，新构造了一个阈值处理函数。该函数较好地满足了其处理后的估计小波系数在设定的阈值处连续并且可导。从测试结果来看，本文提出的算法能较好地去除含噪图像中的噪声，较之传统的软/硬阈值去噪算法具有更好的去噪效果，其所处理的图像能很好地满足目标检测任务的要求。

[1]赵嘉，孙辉，邓承志，等．基于粒子群优化的Shearlet自适应图像去噪[J]．小型微型计算机系统，2011，32(6)：1147-1150．

[2]杨农丰，吴成茂，屈汉章．基于偏微分方程的混合噪声去噪研究[J]．计算机应用研究，2013，30(6)：1899-1902．

[3]张云强，张培林，王国德等．基于曲波变换和色度模型的彩色图像去噪[J]．中国图象图形学报，2012，17(12)：1472-1477．

[4]张力娜，李小林．一种基于小波变换的偏微分方程图像去噪方法[J]．激光与红外，2013，43(8)：943-946．

[5]Mehdi N，Hossein N.Image Denoising in the Wavelet Domain Using a New Adaptive Thresholding Function[J].Neurocomputing, 2009,72(4/6):1012-1025.

[6]Liu W Y，Han JG.The Optimal Mexican HatWaveletfilter Denoising Method Based on Cross-Validation Method[J].Neurocomputing, 2013,108:31-35.

[7]Beenamol M,Prabavathy S,Mohanalin J.Wavelet Based Seismic Signal De-Noising Using Shannon and Tsallis Entropy[J].Computers and Mathematicswith Applications,2012,64(12):3580-3593.

[8]Li J,Cheng C K,Jiang T Y.Wavelet De-Noising of Partial Discharge Signals Based on Genetic Adaptive Threshold Estimation[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2012,19(2):543-549.

[9]Atto A M,Pastor D,Mercier G.Wavelet Shrinkage:Unification of Basic Thresholding Functions and Thresholds[J].Signal Image and Video Processing,2011,5(1):11-28.

[10]Stefan W,Chen KW,Guo H B,et al..Wavelet-Based De-Noising of Positron Emission Tomography Scans[J].Journal of Scientific Computing,2012,50(3):665-677.

[11]Xie Y B,Tang J,Zhou Q.SuppressingWhite-Noise in Partial Discharge Measurements Part1:Construction of Complex Daubechies Wavelet and Complex Threshold[J].European Transactions on Electrical Power,2010,20(6):800-810.

[12]Sanam T F，Shahnaz C.Noisy Speech Enhancement Based on an Adaptive Threshold and a Modified Hard Thresholding Function inWavelet Packet Domain[J].Digital Signal Processing,2013,23(3):941-951.

[13]李旭超，朱善安．小波域图像降噪概述[J]．中国图象图形学报，2006，11(9):1201-1209．

[14]苗常青，汪渤，付梦印等．基于小波分析的电视导引头图像预处理方法[J].弹箭与制导学报,2004,24(1):13-15

[15]Donoho DL,Johnstone IM.Ideal Spatial Adaptation by Wavelet Shrinkage[J].Biometrika，1994,81(3):425-455

[16]DONOHOD L．De-Noising by Soft-Thresholding[J]．IEEE Transactions on Information Theory，1995，41(3):613-627．

[17]朱艳芹，杨先麟．几种基于小波阈值去噪的改进方法[J]．电子测试，2008(2):18-22．

1[8]陶红艳，秦华峰，余成波．基于改进阈值函数的小波域去噪算法的研究[J]．压电与声光，2008,30(1):93-95．

[19]叶重元，黄永东．小波阈值去噪算法的新改进[J]．计算机工程与应用，2011，47(12):141-146．

[20]刘刚，王立香，董延．MATLAB数学图像处理[M]．北京:机械工业出版社，2010:223-250．

[21]郑钧，侯锐峰．小波去噪中小波基的选择[J]．沈阳大学学报，2009，21(2):108-110．

[22]刘召海，杨文柱，张辰．基于变换域的条带噪声去除方法[J]．计算机应用，2013，33(9):2603-2605．

Research on Target Detection Based on Continuous Wavelet Threshold Denoising Algorithm

LIU Bing1，2，LIU Xue-mei3

（1.Dazhou Vocational and Technical College，Dazhou 635001；2.College of Computer and Information Science，Southwest University，Chongqing 400715；3.Statistics Bureau of Dazhou City，Sichuan Province，Dazhou 635000）

The denoising of the noisy image is a recurring work in the target detection task,because of the traditional soft and hard threshold denoising algorithm,the estimated wavelet coefficients have discontinuous and non-derivable defects at the set threshold,often leading to the quality of reconstructed images cannotmeet the requirements of target detection.Analyzes the problems of traditional soft and hard threshold denoising algorithms in detail,and reconstructs a threshold function with continuous derivative at the set threshold.At the same time,gives the corresponding algorithm steps.The simulation results show that the algorithm proposed can remove the noise in the noisy image,which ismore obvious than the traditional softand hard threshold algorithm.The processed image can wellmeet the requirements of further target detection tasks.

刘冰（1970-），男，四川达州人，副教授，研究方向为图像处理、虚拟现实、信息安全等

2017-03-14

2017-05-10

四川省教育厅重点科技计划项目（No.14ZA0330）、四川省达州市2014年科技计划项目（No.2014-8220）

1007-1423（2017）14-0064-05

10.3969/j.issn.1007-1423.2017.14.013

刘雪梅（1975-），女，四川达州人，统计师，研究方向为统计分析与应用等

Image Denoising;Softand Hard Threshold Denoising;ContinuousWavelet Threshold;MSE;PSNR