为什么三角形三个内角的和等于180°？

彭柳萍

一、我的疑惑

证明“三角形三个内角的和等于180°”的方法一般有两种。

方法一：

作直线L，使L平行于三角形的边BC，（如图1）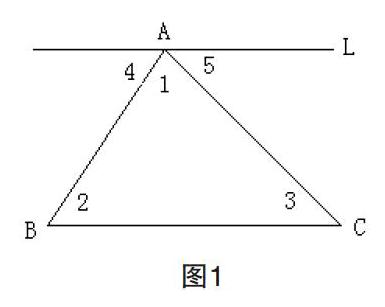

因为∠4+∠1+∠5=平角，

所以∠4+∠1+∠5=180°，（平角等于180°）

因为∠2=∠4，∠3=∠5；（两条直线平行，内错角相等）

所以∠1+∠2+∠3=180°。（等量代换）

方法二：

延长三角形的边BA到点D，作直线L，使L平行于BC，（如图2）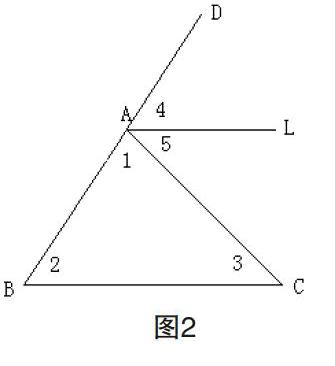

因为∠1+∠4+∠5=平角，

所以∠1+∠4+∠5=180°，（平角等于180°）

因为∠2=∠4，（两条直线平行，同位角相等）

∠3=∠5；（两条直线平行，内错角相等）

所以∠1+∠2+∠3=180°。（等量代换）

小学生还不具备这种“证明”所需要的知识基础，在小学阶段，得到“三角形三个内角的和等于180°”这一结论的教学过程一般是这样的，先让学生画几个不同类型的三角形，通过量一量、算一算，得出三角形三个内角的和等于或接近180°，再让学生通过折一折、撕一斯、拼一拼，得到三角形三个内角拼在一起刚好是一个平角，然后就得出结论。

每次听其他老师上这堂课或者自己教学这个内容时，心中不免忐忑，这样的教学科学吗？通过对几个具体的三角形折腾一番就得出结论，能让学生信服吗？有没有既适合小学生的认知水平，又能使学生更加信服的方法呢？我在教学中做了新的尝试，取得了不错的效果。

二、我的尝试

前面的步骤和原来的基本相同，在让学生通过画一画、算一算、撕一撕、折一折等活动得出“三角形三个内角的和等于180°”这个结论后，我增加了下面这样的环节。

师：大家还有什么疑问吗？

生：……

沉默了一会儿后，平时最爱“较劲”的一个学生举起了手，我投去了赞许的目光。

生1：为什么三角形的内角和都是180°？

师：有想法，谁能回答？

生2：因为三角形的三个角都能拼成一个平角呀！

生1：为什么三角形的三个角都能拼成一个平角呢？

生：哈哈……

一阵哄笑过后，大家陷入了沉默……

师：这确实是一个值得思考的问题，为什么三角形有大有小，有长有短，而内角和都是180°呢？

……

我拿出了课前制作的教具。

师：这是用两根木棒和一根橡皮筋做成的三角形（如图3），谁能利用它说明为什么三角形三个内角的和等于180°？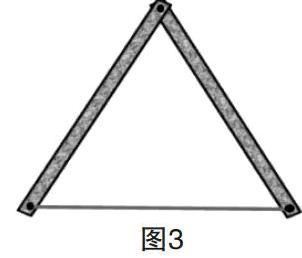

我故意拉了拉兩根木棒的两边，使大家看清楚两根木棒没有钉死，是可以活动的。

有人举起了手。

师：请到上面边演示边说明。

生：这个三角形有三个角，可以把上面这个角叫作角1，下边两个角分别叫作角2和角3，如果角1变大，角2和角3就会变小，角1继续变大，角2和角3就会继续变小，角1越来越接近180°，角2和角3就越来越接近0°，角1等于180°时，角2和角3就变成了0°，不管怎么变，它们的和都是180°。

随着他的演示和说明，学生的眼神渐渐变得明亮。

师：大家觉得他说得有道理吗？

生齐：有道理……

师：掌声！

教室里响起热烈的掌声，上台的同学自信地回到了自己的座位。

师：是啊，三角形其中一个角的度数发生了变化，必然会引起别的角的度数也随着发生变化，而三个角度数的和总是不变的，请看大屏幕。

我让学生观看了几组三角形的动态变化图，然后再问。

师：你们还有什么发现吗？

生1：三角形的一个角变大，另外一个角或者两个角就会变小。

生2：三角形的一个角变小，另外一个角或者两个角就会变大。

生3：三角形的一个角变大，与这个角相对的边也会变长。

……

师：同学们的观察非常仔细，讲得很有道理，其实三角形不单有“内角和等于180°”这个神奇的规律，还有许多知识等着我们去探索，去发现呢！

……

三、我的反思

局限于小学生原有的知识基础和认知水平，在小学阶段很多数学知识无法进行严密的论证，只能通过分析具体的例子，遵循从个别到一般，由具体到抽象的顺序，用归纳总结的方法来获得结论，但是，我们在教学中不能忘记，逐步培养学生的抽象思维能力是数学教学的根本，在教学中，我们要给学生“多问为什么”的机会，让学生的思维由肤浅走向深入，从表象走向实质，使学生不满足于底层次的“发现”止步不前，更不能让学生徘徊在抽象思维的门外沾沾自喜，我们要从学生的实际出发，了解学生的需求，利用他们的好奇心，培养他们的求知欲，在“具体”与“抽象”的夹缝中前行，不断培养学生的思维能力，提高学生的思维水平。