环境因素影响风机MPPT的机理研究

苏勋文，徐殿国，杨荣峰，岳红轩

（1.黑龙江科技大学电气与控制工程学院，黑龙江 哈尔滨 150027；2.哈尔滨工业大学电气工程及自动化学院，黑龙江 哈尔滨 150001；3.许继集团有限公司，河南 许昌 461000）

环境因素影响风机MPPT的机理研究

苏勋文1，2，徐殿国2，杨荣峰2，岳红轩3

（1.黑龙江科技大学电气与控制工程学院，黑龙江 哈尔滨 150027；2.哈尔滨工业大学电气工程及自动化学院，黑龙江 哈尔滨 150001；3.许继集团有限公司，河南 许昌 461000）

为分析环境因素对风机最大功率点跟踪（MPPT）的影响，以环境因素中气压、温度、海拨高度和相对湿度与空气密度的数学关系为基础，从机理上解释了环境因素引起的空气密度变化将改变风机原有的最优功率曲线和最优转矩曲线，并进一步定性分析了环境因素对不同MPPT算法的影响。在Matlab/Simulink分析平台上，搭建了功率信号反馈算法的双馈机组风电场模型。仿真对比了考虑环境因素的MPPT控制与不考虑环境因素的MPPT控制的风机输出特性。结果表明，风机采用考虑环境因素的MPPT控制将提高风机输出功率，从而证实了环境因素影响风机MPPT的机理。

环境因素；最大功率点跟踪；风机；最优功率曲线

在风电机组的实际运行过程中，风电机组输出功率不仅与风速、机组参数、控制策略等有关，还会受到风电场环境因素的影响。

由于环境因素影响，风机所处的不同温度、海拔高度、气压和湿度会导致空气密度随时间波动较大。

目前，大多数风电机组制造商在选择风电机组的控制策略时，仅根据风电场年平均空气密度来确定机组最优控制策略，很少考虑环境因素变化（即空气密度变化）对风电机组输出功率产生的影响，从而导致风电机组输出功率达不到厂家设计的最优输出功率值。

文献［1］综述了风电机组的MPPT算法，把算法分成3大类，即间接功率法（尖速比法、最优力矩法、功率信号反馈法）、直接功率算法（爬山法、电导增量法、最优关系法）、其他算法（模糊算法、神经网络法、扰动观察法），文中指出在不同的环境情况下，间接功率法需要知道空气密度信息，否则将影响风机效率。

文献［2］利用遍历算法，分析了不同温度下，空气密度的增大使得DTG跟踪控制的转矩增益系数Kd和基于收缩跟踪区间跟踪控制的补偿系数a增大。

文献［3］给出了一种自适应空气密度变化的风电机组最优转矩控制方法。但鲜有文献详细揭示环境因素与空气密度的关系以及环境因素对风机MPPT的影响机理。

综上所述，深入研究环境因素对MPPT的影响机理是提高风机输出效率的基础。

为此，本文给出温度、海拨高度、气压和湿度与空气密度的数学关系，分析空气密度变化对风机MPPT的影响机理，深入讨论环境因素对各种风机MPPT算法的影响。最后通过仿真进行验证。

1 环境因素与空气密度数学模型

影响空气密度的环境因素有气压、温度、海拨高度和湿度［4］。根据风机所处的不同地理环境，有些影响空气密度的因素不需考虑，比如海上风电场不需要考虑海拨高度，而山区风电场需考虑。为此，给出3组环境因素与空气密度的数学模型。

1.1 气压和温度与空气密度的数学模型

当不考虑湿度和高度时，空气密度仅与气压和温度有关，其数学关系为

式中：ρ为10 min的平均空气密度；P为10 min的测量平均气压；R0为干燥空气的气体系数，取287.05 J/（kg·K）；T为10 min的平均测量温度，计算时取T=TC+273.15，TC为实际温度值。

图1给出了气压、温度与空气密度的关系曲线，可以看出，随着气压降低和温度升高，空气密度将变小。

图1 气压和温度与空气密度函数关系Fig.1 Air density as function of barometric pressure and temperature

1.2 高度和温度与空气密度的数学模型

空气密度与高度和温度的关系式为

式中：P0为标准大气压，101 325 Pa；T0为标准温度，15+273.15=288.15℃；L为温度递减率，0.006 5 K/m；H为高度，m；g为重力加速度，9.806 65 m/s2。

图2给出了高度和温度与空气密度的关系曲线，可以看出，随着高度增加和温度升高，空气密度将变小。

图2 高度和温度与空气密度函数关系Fig.2 Air density as function of altitude and temperature

1.3 湿度、气压和温度与空气密度的数学模型

基于特腾斯公式（Tetens formula）的饱和水蒸气压力为

式中：C0,C1,C2分别为特腾斯公式的系数；C0为6.107 8；C1为7.5；C2为237.3。

相对湿度定义为实际水蒸气压力和饱和水蒸气压力的比值，计为PH%。实际水蒸气压力为

考虑湿度的空气密度计算公式为

还有2个表征湿度的物理量是露点温度和绝对湿度，他们与相对湿度可相互转化。

图3给出了相对湿度、温度与空气密度的关系曲线。

图3 相对湿度和温度与空气密度函数关系Fig.3 Air density as function of relative humidity and temperature

由图3可以看出，随着相对湿度变大和温度升高，空气密度将变小。但在温度较低时，相对湿度对空气密度影响不大，而气温较高时，需要计及相对湿度对空气密度的影响。

2 环境因素的MPPT影响机理

2.1 MPPT原理

由空气动力学和贝兹准则可知，风力机从风能中捕获的机械功率为［1］

式中：ρ为空气密度；R为风机叶轮半径；vw为风速；λ为叶尖速比；β为桨距角；Cp为叶片的风能利用系数。

机械力矩为

式中：ωm为机械转速。

叶尖速比为

风能利用系数的一种解析法计算方法如下：

本文采用式（9）的风能利用系数计算方法，假定桨距角β为0，其Cp—λ曲线如图4所示。

图4 Cp—λ曲线Fig.4 Cp—λcurve

从图4可以看出，当λ取6.325时，Cp最大为0.438 2，此时风机的输出功率最大。对于特定的风速，存在唯一的转速使得风能转换效率最高。连接不同风速的最优功率运行点，得最优功率曲线，如图5所示。

图5 最优功率曲线Fig.5 Maximum power curves

2.2 环境因素对MPPT曲线的影响

风机的环境因素时时刻刻都在变化，当风机所处的海拨高度、气压、温度、相对湿度有变化时，风机输入风能的空气密度也会发生变化。空气密度分别取1.1 kg/m3，1.2 kg/m3，1.3 kg/m3，1.4 kg/m3，图6给出风速为8 m/s，空气密度不同时风机输出功率和转速的特性曲线。

图6 空气密度不同的PM—ω曲线Fig.6 PM—ωcurves for different air densities

从图6可以看出，随着空气密度的变大，风机的输出功率增加。但不同空气密度时风电机组最大功率对应的转速不变。原因是式（8）叶尖速比的计算公式中没有空气密度变量，因此最优转速不受空气密度变化影响。风速分别取7 m/s，8 m/s，9 m/s，图7给出空气密度分别为1.1 kg/m3，1.2 kg/m3，1.3 kg/m3的风机最优功率曲线。

图7 空气密度不同的最优功率曲线Fig.7 Maximum power curves for different air densities

从图7可以看出，当空气密度变化时，风机的最优功率曲线会变化，如果不监控空气密度，当空气密度变化时，还按照原来的最优功率曲线控制风机运行，风电机组的输出性能将不是最优。

3 环境因素对MPPT算法的影响

下面分别介绍几种MPPT算法，结合上节的环境因素对风机MPPT的影响机理，分析环境因素对MPPT算法的影响。

3.1 叶尖速比算法

叶尖速比方法［1，5］是在风速变化时，保持风机的叶尖速比λ处于最优叶尖速比λopt，它是通过风速测量和风电机组转速测量，得到最优功率跟踪的方法。控制方法如图8所示。

图8 叶尖速比MPPT算法Fig.8 Tip speed ratio MPPT algorithm

环境因素会改变空气密度，从式（8）和式（9）可以看出叶尖速比计算和最优转速的计算公式中没有空气密度，因此环境因素不影响叶尖速比MPPT算法，但由于该算法需要风速测量，这会增加成本，且难以准确测量风速。

3.2 最优转矩算法

根据式（7）～式（9），把最优叶尖速比和最大风能利用系数带入风机转矩计算公式，可以计算出最优机械转矩如下式，该转矩与转速的平方成正比，然后和实际转矩进行比较控制。控制算法如图9所示［1］。

式中：Kopt为转速的立方与最优转矩的关系系数。

图9 最优转矩MPPT算法Fig.9 Optimal torque MPPT algorithm

根据式（10）可以得出风机最优转矩-转速曲线，如图10所示。

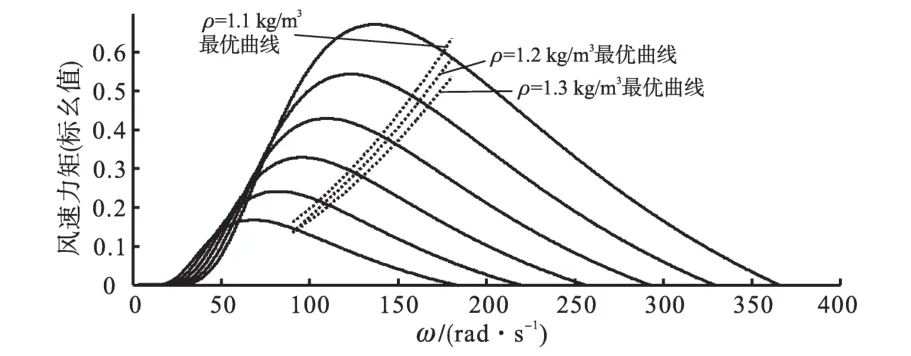
图10 空气密度不同的最优转矩曲线Fig.10 Maximum torque curve for different air densities

图10中，实线由下至上是空气密度为1.2kg/m3、风速为5～10 m/s的风机力矩-转速特性曲线；虚线表示空气密度为1.1～1.3 kg/m3的风机最优转矩曲线。可以看出，当空气密度变化时，风机最优转矩曲线也会发生变化。

当环境因素变化，空气密度从 ρ1变成 ρ2。从图10可以看出空气密度变化后，最优转矩曲线也发生变化，相同转速对应的最优转矩比值为

由此可见，当环境因素变化时需要修订最优转矩算法的Kopt值中的空气密度［3］。

3.3 功率信号反馈算法

已知风机的最优功率曲线、输入转速，通过最优功率曲线查到对应的最优功率值，最优功率值与实际功率进行比较控制，其控制算法如图11所示［1，6］。

图11 功率信号反馈MPPT算法Fig.11 Power signal feedback MPPT algorithm

从图7可以看出空气密度变化后，最优功率曲线也发生变化，相同转速对应的最优功率比值为

由此可见，当环境因素变化时需要修订最优转矩算法的Kopt值中的空气密度。

3.4 爬山搜索及其改进算法

爬山搜索算法［1，7］不同于前面的算法，可以不依赖风速测量和风机特性参数，持续地搜索风机输出功率最大值。但该算法存在极值点附近震荡搜索、搜索方向误判、不适合转动惯量较大的机组等缺陷［8］。为此，提出了改进的变步长爬山搜索算法［9］。当环境因素和风速变化后，其运行点为A点，首先根据运行点功率和最优功率曲线找到对应功率曲线的B点，该运行点与最优功率曲线的距离为ω-ω*，然后取控制器搜索步长为β(ω-ω*)，β是正系数。可以看出，如果距离最优功率曲线较远，则用大步长，如果接近最优功率曲线，则步长变小，最后达到C点最大功率输出点。其自适应变步长跟踪方法如图12所示。

图12 自适应变步长跟踪Fig.12 Adaptive tracking with variable step size

当环境因素变化时，以文献［10］的爬山算法为例，风机的空气密度会发生变化，将会对该算法产生3方面的影响：

1）算法模式0中ω*计算公式需要考虑Kopt空气密度的变化；

2）模式2中的变搜索步长 β(ω-ω*)，需要考虑空气密度变了后，根据图7最优功率曲线也发生了变化，ω*的计算也会发生变化；

3）算法中模式的切换需要判断风速是否变化，文中给出一种不需要测风仪的风速判断方法，但该方法没有考虑空气密度变化的情况，空气密度的变化同样会引起模式的切换。

3.5 人工智能算法

基于模糊算法和神经网络［1，11］的MPPT算法，如果环境因素变化，则需要一定的时间进行样本的训练，否则风机效率可能达不到最优。或者根据环境因素进行样本训练，当环境因素变化后，直接找到环境变化后对应的最优控制数值。

4 仿真验证

在Matlab/Simulink中建立了基于功率信号反馈算法的双馈机组风电场模型，图13是风电场算例的结构示意图。该风电场由100台2 MW双馈风电机组组成，假定所有机组感受相同的风速，采用1台等值风电机组表征风电场模型，风电机组经机端负荷和变压器（110 kV/690 V）连接到外部电网。风电机组发电机主要参数为：额定功率2 MW，额定电压690 V，额定频率50 Hz，Rs=0.010 08（标幺值），Rr=0.010 21（标幺值），Xm=3.362（标幺值），Xs=0.102（标幺值），Xr=0.11（标幺值），H=3 s，F=0.01（标幺值）。

图13 风电场系统单线示意图Fig.13 Single line diagram of wind farm

为了验证环境因素对风机MPPT的影响，假定环境因素变化，使得空气密度由标准空气密度增加到1.2倍标准空气密度。分别进行下列3种情况的仿真：

1）标准空气密度，MPPT控制采用基于功率信号反馈算法；

2）1.2倍标准空气密度，原有MPPT控制（即MPPT同前）；

3）1.2倍标准空气密度，根据式（13），采用考虑环境因素变化的MPPT控制。

输入风速如图14所示，仿真时间60 s。图15给出了3种情况下风机转速的特性曲线（取系统稳定后10～60 s）。

图14 风速Fig.14 wind speed

图15 风机转速Fig.15 Rotor speed of wind turbine

图16～图18给出了3种情况下风能利用系数、风力机转矩、风机输出功率的特性曲线（取系统稳定后10～60 s）。

图16 风机风能利用系数Fig.16 power coefficient of wind turbine

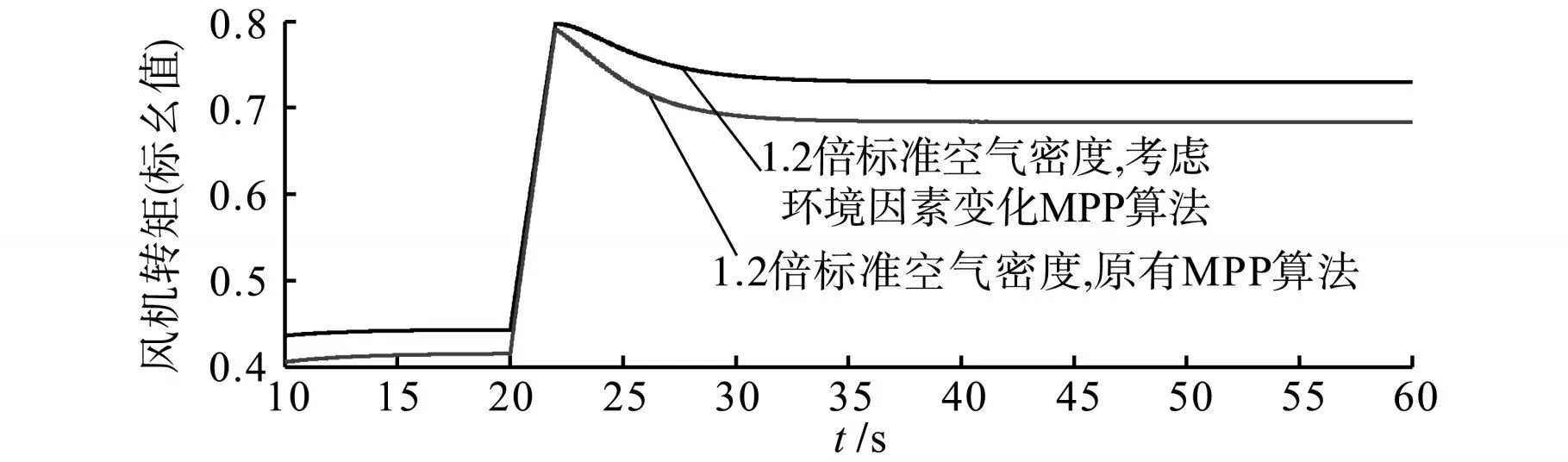
图17 风机转矩Fig.17 Torque of wind turbine

图18 风机输出功率Fig.18 Output power of wind turbine

结合图6和图15可以看出，图15中实线和虚线几乎重合，说明当环境因素改变后，空气密度发生变化，但同一风速下对应的最优转速不变，从而验证了图6的原理。图15中1.2倍标准空气密度，原有MPPT算法中，则风机转速略高，而不是最优转速，所以图16中虚线的风能利用系数较低。注意到当风速变化期间，虚线风能利用系数相对较高的原因是此时风机输出较低，加速了风机转子的跟踪速度。

从图17的风力机机械转矩和图18的风机输出功率可以看出考虑环境因素变化的MPPT控制相比不考虑环境因素变化的情况将获得更大的机械力矩和输出功率，从而证实了环境因素对风机MPPT的影响机理。

另外，已将环境因素影响考虑到风机MPPT的实际应用中，目前该课题合作单位正在国家风光储输（张北）示范风电场进行测试，已完成阶段测试，测试的参数精度是：温度的测量误差是在1℃以内，气压的精度在98%以上，通过风机功率曲线对比，考虑环境因素MPPT控制的风机功率曲线优于没有考虑环境因素MPPT控制的风机功率曲线，特别在风速为8～12 m/s之间时该优势更加明显。

5 结论

1）环境因素中的气压、海拔高度、温度和相对湿度影响空气密度的大小。当环境因素变化后，风电机组的最优功率曲线和最优转矩曲线也会发生变化。

2）当环境因素变化后，风机MPPT的大部分算法也要进行相应的修改，否则将影响风机的风能转换效率。

［1］Dipesh Kumar，Kalyan Chatterjee.A Review of Conventional and Advanced MPPT Algorithms for Wind Energy Systems［J］.Renewable and Sustainable Energy Reviews，2016，55：957-970.

［2］张小莲，殷明慧，周连俊，等.风电机组最大功率点跟踪控制的影响因素分析［J］.电力系统自动化，2013，37（22）：15-21.

［3］楚峥，李楠.自适应空气密度变化的风电机组最优转矩控制［J］.上海电气技术，2014，7（2）：41-44.

［4］Picard A，Davis R S，Glser M，et al.Revised Formula for the Density of Moist Air（CIPM-2007）［J］.Metrologia，2008，45（2）：149-155.

［5］Abdullah M A，Yatim A H M，Tan C W，et al.A Review of Maximum Power Point Tracking Algorithms for Wind Energy Systems［J］.Renewable and Sustainable Energy Reviews，2012，16（5）：3320-3327.

［6］陈家伟，陈杰，龚春英.变速风力发电机组恒带宽最大功率跟踪控制策略［J］.中国电机工程学报，2012，32（27）：32-38.

［7］林济铿，仵光宇，孙峰，等.计及疲劳载荷基于极值搜索控制的风电系统最佳出力追踪［J］.中国电机工程学报，2014，34（17）：2826-2835.

［8］张小莲，李群，殷明慧，等.一种引入停止机制的改进爬山算法［J］.中国电机工程学报，2012，32（14）：128-134.

［9］Wang Q，Chang L.An Intelligent Maximum Power Extraction Algorithm for Inverter-based Variable Speed Wind Turbine Systems［J］.IEEE Transactions on Power Electronics，2004，19（5）：1242-1249.

［10］Kazmi SMR，Goto H，Guo H-J，et al.A Novel Algorithm for Fast and Efficient Speed-sensorless Maximum Power Point Tracking in Wind Energy Conversion Systems［J］.IEEE Transactions on Industrial Electronics，2011，58（1）：29-36.

［11］殷明慧，张小莲，邹云，等.跟踪区间优化的风力机最大功率点跟踪控制［J］.电网技术，2014 ，38（8）：2180-2185.

Mechanism Research on the Effects of Environmental Factors for Wind Turbine MPPT

SU Xunwen1，2，XU Dianguo2，YANG Rongfeng2，YUE Hongxuan3
（1.Institute of Electrical and Control Engineering，Heilongjiang University of Science and Technology，Harbin 150027，Heilongjiang，China；2.School of Electrical Engineering and Automation，Harbin Institute of Technology，Harbin 150001，Heilongjiang，China；3.Xuji Group Corporation，Xuchang 461000，Henan，China）

To analyze the effects of environmental factors on MPPT of wind turbine，basing on the mathematical relationships of air pressure，temperature，altitude and relative humidity in environmental factors with air density，it was explained that the change of air density caused by environmental factors will change the original optimal power curve and optimal torque curve of the wind turbine from the mechanism.Furthermore，the influence of environmental factors on different MPPT algorithms was analyzed qualitatively.Based on power signal feedback MPPT algorithm，wind farm with doubly fed induction generator wind turbines was built on Matlab/Simulink platform.The MPPT control considering the environmental factors and the MPPT control without considering the environmental factors were simulated and compared.Analysis results show that the MPPT algorithm considering the environmental factors can increase output power of wind turbine，thus it can confirm that the environmental factors affect MPPT algorithm.

environmental factors；maximum power point tracking（MPPT）；wind turbine；optimal power curve

TM315

A

10.19457/j.1001-2095.20170613

2016-03-06

修改稿日期：2016-05-02

国家电网公司科技项目资助（SGSDDK00KJJS1500155）；国家自然科学基金重点项目（51237002）；

国家自然科学基金（51677057）；2015年哈尔滨市科技创新人才研究专项资金（青年后备）项目（RC2015QN007019）；博士后研究人员落户黑龙江科研启动项目（LBH－Q15125）

苏勋文（1976-），男，博士后，副教授，Email：suxunwen@163.com