非隔离型光伏并网逆变器共模电流抑制

李奎，韩振铎，牛峰，王尧

（河北工业大学电磁场与电器可靠性省部共建国家重点实验室培育基地，天津 300130）

非隔离型光伏并网逆变器共模电流抑制

李奎，韩振铎，牛峰，王尧

（河北工业大学电磁场与电器可靠性省部共建国家重点实验室培育基地，天津 300130）

非隔离型光伏并网系统共模电流较大，其大小受控制方法的直接影响。首先阐述系统共模电流产生机理，然后在分析传统直接功率控制原理的基础上提出一种基于新型开关表和性能指标评估函数的模型预测直接功率控制方法，该方法通过权衡各个控制性能指标之间耦合关系实现最优电压矢量的选择。对提出的方法进行了仿真实验研究，并与传统直接功率控制方法进行了详细对比分析，结果表明提出的方法不仅可以有效抑制系统共模电流，同时能够降低输出功率脉动，验证了该方法的可行性和有效性。

非隔离型光伏并网逆变器；共模电流；模型预测直接功率控制；性能指标评估函数

光伏并网系统作为一种高效的分布式发电系统越来越广泛地被接入到现代智能电网中，其中并网逆变器作为光伏发电与电网的连接设备，其性能优劣直接影响到电网系统的高效可靠运行。非隔离型光伏并网逆变器具有体积小、成本低和效率高等优点，近年来得到了广泛关注［1-3］。然而由于非隔离型光伏并网逆变器舍弃了隔离变压器，使得光伏系统与电网之间存在电气连接，导致系统存在高幅值、高频率的共模电流，对系统的安全可靠运行带来隐患。因此，如何消除光伏并网系统中的共模电流已成为国内外研究的主要热点［4-7］。

关于三相非隔离型光伏并网系统共模电流的抑制方法，简单有效的是将光伏阵列直流侧中点、电网交流侧中点与大地二者连接［4］，忽略大地之间的阻抗Lg和直流侧/交流侧中点之间的阻抗Z，直流侧/交流侧中点与大地连接可使得光伏板与大地之间寄生电容两端的电压为常量，从而达到抑制共模电流的效果。文献［6］参考电机驱动系统共模电流的抑制方法［5］，通过3个非零矢量合成所需矢量来抑制光伏并网系统共模电流。相比于矢量控制，直接功率控制（DPC）［8］不涉及复杂的坐标变换和空间矢量脉宽调制（SVPWM），具有控制结构简单、动态响应快等优点，但是关于DPC对光伏并网系统共模电流进行抑制的文献报道很少。

本文以三相非隔离型光伏并网逆变器为研究对象，首先对光伏并网系统共模电流进行分析，然后介绍传统DPC工作原理［8］，最后提出一种基于新型开关表和性能指标评估函数的模型预测直接功率控制方法（MPDPC），并对上述2种控制方法进行仿真实验和对比分析，验证本文所提方法的有效性和优越性。

1 系统共模电流分析

图1为典型的三相非隔离型光伏并网系统结构图［9］。其中Ea,Eb,Ec为电网三相交流电压；L和R分别为并网接口电感和电阻；Cpv为光伏板与大地之间的寄生电容，其值与外部环境条件、光伏板尺寸结构等因素有关，一般在50～150nF/kW左右［6］。

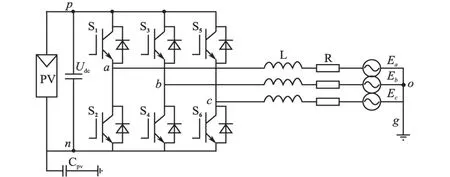
图1 三相非隔离型光伏并网系统Fig.1 Three-phase non-isolated PV grid-connected system

光伏并网系统正常运行时，根据共模电压定义［9］，可得并网逆变器输出的共模电压为

三相两电平光伏并网逆变器可直接输出8个空间电压矢量，包括6个有效矢量U1，U3，U5（奇矢量），U2，U4，U6（偶矢量）和2个零矢量U0，U7。由式（1）可计算不同电压矢量对应的共模电压，如表1所示。

表1 电压矢量与对应的共模电压Tab.1 Voltage vectors and corresponding common mode voltage

共模电流计算公式为

由式（2）可知，系统共模电流大小与共模电压的变化率和变化量有关。并网逆变器输出不同电压矢量时输出的共模电压也会变化，进而在逆变器、光伏板寄生电容与电网组成的回路中形成高频共模电流。

2 传统直接功率控制

由图1可知三相并网系统输出电流在α-β坐标系下的动态方程为

式中：Uα,β，iα,β分别为并网逆变器输出电压和电流在静止坐标系中的α,β分量；Eα,β为电网电压在静止坐标系中的α,β分量。

并网逆变器输出的瞬时有功、无功功率在α-β坐标系下可以表示为

对式（4）求导并忽略电阻压降，可得瞬时功率的变化率为

如果控制周期为Ts，认为电网电压在1个控制周期内保持不变，分别对式（3）和式（5）进行一阶前向欧拉离散，可得：

将式（6）代入式（7）可得：

其中 ΔP=P(k+1)-P(k) ΔQ=Q(k+1)-Q(k)

文献［15］将矢量空间分为12个扇区，根据式（8）可得各个扇区中不同空间电压矢量作用下有功、无功功率变化量ΔP,ΔQ的波形，如图2所示。

图2 不同空间电压矢量作用下ΔP,ΔQ波形Fig.2 The behaviors ofΔP,ΔQunder different space voltage vectors

根据图2得出的开关表中1、2扇区的电压矢量相同，本文将其合并为1个扇区θ1，依此类推，得到的开关表如表2所示。ΔP＞0时，SP=1，ΔP＜0时，SP=0，同理可得ΔQ对应的SQ值。

表2 DPC开关表Tab.2 SwitchingtableofDPC

3 模型预测直接功率控制

3.1 控制原理

传统DPC的有功和无功功率脉动较大，且未考虑共模电流的抑制，这主要是由于传统DPC在1个控制周期内根据滞环输出信号SP，SQ的取值只作用表2所给出的电压矢量，而忽略了其它电压矢量所包含的信息，从而降低系统控制性能。针对这一问题，本文提出基于新型开关表和性能指标评估函数的模型预测直接功率控制。该方法的控制思想是预测不同电压矢量作用下光伏并网系统的运行状态，并对不同电压矢量的预测结果进行控制性能评估，选取综合误差最小的电压矢量为最优电压矢量。为尽可能包含多的可供选择电压矢量，通过对图2详细分析可知，在1扇区内，当SP=0，SQ=1时，可以通过施加电压矢量U5或U6而达到有功功率减小且无功功率增加。同理可得SP，SQ为其它情况时，可供选择的电压矢量，如表3所示。按照上面电压矢量在1扇区内的作用关系，可得其它扇区的各电压矢量作用关系，如表4所示。

表3 电压矢量在1扇区作用关系Tab.3 Relationships space vectors in the sector

表4 MPDPC开关表Tab.4 Switching table of MPDPC

MPDPC方法实施流程如下：在k时刻，计算系统有功和无功功率实时值，根据表4和式（8）预测并记录不同电压矢量作用下k+1时刻的系统有功和无功功率误差，同时预测和记录相应的共模电压变化量。预测过程结束后，对不同电压矢量的预测结果进行误差评估，选定综合误差最小的电压矢量作为下一控制周期的输出电压矢量。

3.2 性能指标评估函数

本文采用下式所示的性能指标评估函数对共模电压变化量、有功功率误差和无功功率误差进行综合误差评估，最后选取综合误差最小的电压矢量为最优电压矢量。

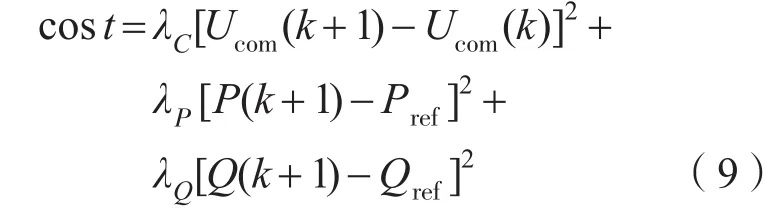
式中：Ucom(k+1),P(k+1)和Q(k+1)分别为共模电压、有功功率和无功功率预测值；Ucom(k)是k时刻输出的共模电压；Pref和Qref分别为有功功率和无功功率期望值；为了平衡各个控制性能指标在综合误差中所占比重，引入相应的权重系数进行调节，λC,λP和λQ分别为3个相应的权重系数。

本文所提方法的控制目标是在不影响输出功率脉动的前提下，有效抑制系统共模电流。其控制策略为：如果k时刻采用的电压矢量是奇矢量或偶矢量，则k+1时刻优先选用相应的奇矢量或偶矢量，使共模电压变化量为零，从而降低系统共模电流。以上控制策略的实现可以通过增大权重系数λC实现。此外，在实际应用中，各权重系数的取值可以根据共模电压、有功功率和无功功率的脉动幅值进行调节，以实现不同控制目标。

4 仿真实验验证

为验证本文所提方法的可行性与有效性，在Matlab/Simulink环境下进行仿真，系统框图如图3所示。系统相关参数为：直流母线电压Udc=500 V，电网电压有效值EArms=100 V，三相输出电感Li（i=a，b，c）=25 mH，寄生电容Cpv=100 nF，控制周期Ts=50 μs。

图3 三相光伏并网系统MPDPC框图Fig.3 The block diagram of MPDPC for three⁃phase PV grid⁃connected system

共模电流有效值通过下式计算：

式中：IRms为共模电流有效值；m为采样点数。

有功和无功功率脉动通过下式计算：

式中：Prip，Qrip分别为有功功率脉动和无功功率脉动；Pavg，Qavg分别为有功功率和无功功率的平均值。

4.1 基本控制性能对比分析

本文首先对DPC和MPDPC的基本控制性能进行对比分析，图4和图5分别为有功功率变化和无功功率变化时DPC和MPDPC对比图。图中从上至下分别为有功功率和无功功率、三相电流、共模电压和共模电流，其中图4b和图5b中权重系数为：λC=20，λP=15，λQ=15。

图4为光伏并网逆变器有功功率Pref由1000 W跃升至1 500 W、无功功率Qref=0时的波形。有功功率Pref为1 000 W时，MPDPC的有功功率脉动比DPC降低了约11%，无功功率脉动和电流THD与DPC基本相同，但是MPDPC的共模电流有效值比DPC降低了约59%。当Pref从1 000 W阶跃到1 500 W时，MPDPC和DPC的输出功率脉动、电流THD基本相同，但是MPDPC的共模电流有效值比DPC降低了约56%。

图4 有功功率改变时DPC和MPDPC对比图Fig.4 Comparison between DPC and MPDPC under different active power

图5为光伏并网逆变器有功功率Pref=1500W、无功功率Qref由0跃升至500 W时的波形。无功功率Qref为0时，MPDPC的有功功率脉动比DPC降低了约11%，无功功率脉动与DPC基本相同，MPDPC的电流THD优于DPC，同时MPDPC的共模电流有效值比DPC降低了约62%。当Qref从0阶跃到500 var时，MPDPC的无功功率脉动比DPC升高了约11%，有功功率脉动和电流THD与DPC基本相同。但是，MPDPC的共模电流有效值比DPC降低了约51%。

图5 无功功率变化时DPC和MPDPC对比图Fig.5 Comparison between DPC and MPDPC under different reactive power

通过上述结果可知，并网逆变器无论工作在单位功率因数下还是在无功补偿状态下，MPDPC的输出功率脉动和电流THD与DPC基本相同甚至优于DPC，但是MPDPC的共模电流有效值明显低于DPC。此外，在改变功率给定时，MPDPC和DPC的输出功率都能很快跟随给定值，具有很好的动态性能。

4.2 权重系数变化对比分析

本文在对2种方法的基本控制性能进行研究的基础上，还对MPDPC在不同权重系数和不同输出功率下的控制性能进行了详细对比分析。图6为系统在有功功率Pref=1 500 W、无功功率Qref=0的情况下，权重系数λC在不同取值下的波形。权重系数初始值为：λC=15,λP=15,λQ=15,在0.09 s时变为：λC=22，λP=15，λQ=15。

从图6中可以看出，随着权重系数λC的增大，MPDPC的输出功率脉动增加了约7%，电流THD增加了约6.6%，但是共模电流有效值降了约24%。

图6 MPDPC权重系数变化对比图Fig.6 The comparison of MPDPC weight ratio change

图7为不同有功功率下DPC和MPDPC的共模电流、有功功率脉动和无功功率脉动的对比图，其中为简化MPDPC权重系数变化时的图例，使用@12，@17，@23和@27分别表示MPDPC的权重系数，λC∶λP∶λQ分别为：12∶15∶15，17∶15∶15，23∶15∶15和27∶15∶15。

图7 DPC和MPDPC在不同有功功率下对比图Fig.7 Comparison between DPC and MPDPC under different active power

从图7可以看出，随着λC的增大，MPDPC的共模电流有效值明显降低，但是有功功率脉动和无功功率脉动会相应增大。也就是说，可以根据实际应用场合对相应的权重系数进行调节，使系统达到最优运行性能。同理，可以通过调节权重系数λP和λQ的大小调节有功和无功功率脉动，由于篇幅限制，本文不再给出λP和λQ改变时的波形图。

5 结论

本文针对非隔离型光伏并网系统中共模电流较大的问题，首先对传统直接功率控制进行研究，在此基础上提出一种基于新型开关表和性能指标评估函数的模型预测直接功率控制方法，该方法通过权衡各个控制性能指标之间的耦合关系确定最优电压矢量。通过仿真实验验证了本文所提方法不仅能够有效抑制系统共模电流，同时能够降低系统输出功率脉动，在光伏并网系统中具有一定的应用价值。

［1］Kjaer S B，Pedersen J K，Blaabjerg F.A Review of Sin⁃gle-phase Grid-connected Inverters for Photovoltaic Modules［J］.IEEE Transactions on Industry Applications，2005，41（5）：1292-1306.

［2］Quan L，Wolfs P.A Review of the Single Phase Photovoltaic Module Integrated Converter Topologies with Three Different DC Link Configurations［J］.IEEE Transactions on Power Electronics，2008，23（3）：1320-1333.

［3］王宝诚，郭小强，梅强，等.无变压器非隔离型光伏并网逆变器直流注入控制技术［J］.中国电机工程学报，2009，29（36）：23-28.

［4］Kerekes T，Teodorescu R，Liserre M，et al.Evaluation of Three-phase Transformerless Photovoltaic Inverter Topologies［J］.IEEE Transaction on Power Electronics，2009，24（9）：2201-2211.

［5］Hava A M，Un E.Performance Analysis of Reduced Com⁃mon-mode Voltage PWM Methods and Comparison with Stan⁃dard PWM Methods for Three-phase Voltage-source Inverters［J］.IEEE Transactions on Power Electronics，2009，24（1）：241-252.

［6］Cavalcanti M C，De Oliveira K C，De Farias A M，et al.Modu⁃lation Techniques to Eliminate Leakage Currents in Transfor⁃merless Three-phase Photovoltaic Systems［J］.IEEE Transac⁃tions on Industrial Electronics，2010，57（4）：1360-1368.

［7］Yang B，Li W H，Gu Y J，et al.Improved Transformerless In⁃verter with Common-mode Leakage Current Elimination for a Photovoltaic Grid-connected Power System［J］.IEEE Transac⁃tions on Power Electronics，2012，27（2）：752-762.

［8］杨勇，阮毅.三相并网逆变器直接功率控制［J］.电力自动化设备，2011，31（9）：54-59.

［9］邬伟扬，郭小强.无变压器非隔离型光伏并网逆变器漏电流抑制技术［J］.中国电机工程学报，2012，32（18）：1-8.

Common Mode Current Suppression for Non-isolated Photovoltaic Grid-connected Inverters

LI Kui，HAN Zhenduo，NIU Feng，WANG Yao
（Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability，Hebei University of Technology，Tianjin 300130，China）

The common mode current in non⁃isolated photovoltaic（PV）grid⁃connected systems is large，which is mainly affected by the control method.The generation mechanism of system common mode current and the traditional direct power control（DPC）were analyzed，and a novel model predictive direct power control（MPDPC）strategy was proposed based on the new switching table and performance evaluation function.The MPDPC could select the optimal voltage vector by weighting the coupling between the various control performance index.Simulation experiments of the proposed MPDPC were carried out and the comparison of MPDTC and DPC were conducted.The results show that the proposed MPDPC can be able to suppress common mode current and reduce the output power ripples，which verifies the feasibility and validity of the proposed MPDPC.

non-isolated PV grid-connected inverters；common mode current；model predictive direct power control（MPDPC）；performance evaluation function

TM464

A

10.19457/j.1001-2095.20170605

2016-05-03

修改稿日期：2016-08-01

河北省高等学校自然科学青年基金项目（QN2016193，QN2014148）；

河北省高等学校创新团队领军人才培育计划（LJRC003）

李奎（1965-），男，博士，教授，Email：likui@hebut.edu.cn