Stable t-structures and Homotopy Category of Strongly Copure Projective Modules

Ma Xin and Zhao You-yi

(College of Natural Sciences,Gansu Agricultural University,Lanzhou,730070)

Stable t-structures and Homotopy Category of Strongly Copure Projective Modules

Ma Xin and Zhao You-yi

(College of Natural Sciences,Gansu Agricultural University,Lanzhou,730070)

Communicated by Du Xian-kun

In this paper,we study the homotopy category of unbounded complexes of strongly copure projective modules with bounded relative homologiesK∞,bscp(SCP). We show that the existence of a right recollement ofK∞,bscp(SCP)with respect toK−,bscp(SCP),Kscpac(SCP)andK∞,bscp(SCP)has the homotopy category of strongly copure projective acyclic complexes as a triangulated subcategory in some case.

homotopy category,recollement,stablet-structure

1 Introduction and Preliminaries

As we know,triangulated categories play an important role on communicating algebraic reprensentability theory with algebraic geometry.The recollements andt-structures of triangulated categories introduced by Beilinsonet al.[1]are the key factors in this process. Recollements of triangulated categories with the idea thatTcan be viewed as being“glued together”fromT′andT′′.The canonical example of a recollement hasT,T′andT′′equal to suitable derived categories of sheaves on spacesX,ZandU,whereXis the union of the closed subspaceZand its open complementU.Miyachi[2]introduced the stablet-structure of triangulated categories,which relates the recollements.

In Section 2,we study some properties of strongly copure projective acyclic complexes. In Section 3,letSCPbe the category of strongly copure projectiveR-modules,which are also called stronglyP-projective modules.The notion is introduced by Mao[3],Mis said to be stronglyP-projective module iffor all projective leftR-modulesP,which is dual to the notion of strongly copure injectiveR-modules in[4].So we call them strongly copure projective modules in this paper,which is a generalization of Gorenstein projective modules.We consider the relation of the homotopy categoryof unbounded complexes with bounded relative homologies,its subcategoriesand the homotopy categoryof strongly copure projective acyclic complexes. We show that the existence of a right recollement of the homotopy categoryand it hasas a triangulated subcategory whenRis ann-FC ring.

Next we recall some known notions and facts needed in the sequel.

LetRbe a ring with unity andC(R)the category of complexes ofR-modules.A complexXinC(R)is said to be bounded below if there exists anN∈Zsuch thatXn=0 forn≤Nand bounded above if there exists anN∈Zsuch thatXn=0 for alln≥N.A complex is bounded if it is both bounded above and bounded below.We de fine three full subcategories ofK(R):

K+(R):bounded below complexes;

K−(R):bounded above complexes;

Kb(R):bounded complexes.

LetXbe inC(R)andn∈Z.We de fine another complex inC(R)by“shifting”nplaces to the left(writing cochain complexes with indices ascending to the right)

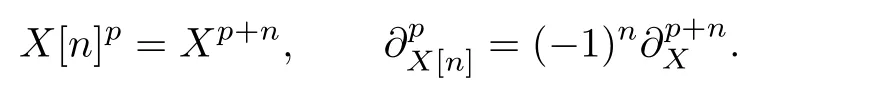
Ifis a morphism of complexes,thende fines a morphism of complexes

Letf:X−→Ybe a morphism of complexes.is a quasi-isomorphism if the morphismis an isomorphism of abelian groups for everyThe mapping cone Cone(f)offis de fined forn∈Zbywith the di ff erentialf:is a quasi-isomorphism if and only if the mapping cone Cone(f)is acyclic.

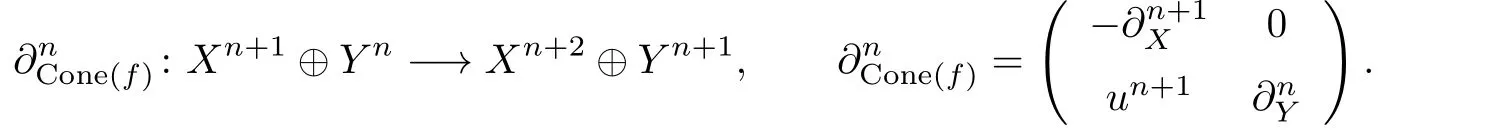
The homotopy categoryK(R)is the category whose objects are complexes inC(R)and whose morphisms are homotopy equivalence classes of morphisms of complexes.That is,we begin with the abelian categoryC(R)and use the homotopy equivalence relation to divide the morphism sets up into equivalence classes.As we all know,K(R)is a triangulated category with triangulations.

2 Strongly Copure Projective Acyclic Complex

This section is to introduce and study the strongly copure projective acyclic complex.

De finition 2.1A complex X∗is strongly copure projective acyclic,or simply,SCP-acyclic,ifis acyclic for all strongly copure projective R-modules M.

Since every projectiveR-module is strongly copure projective,SCP-acyclic complex is acyclic.

De finition 2.2HomR(M,f∗)is a quasi-isomorphism for any strongly copure projective R-module M,i.e.,there are isomorphisms of abelian groups

Lemma 2.1Ifis an SCP-acyclic complex,then for any i,the truncation

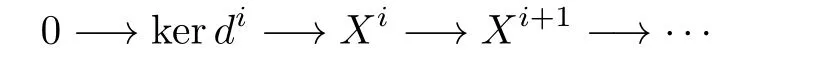
and

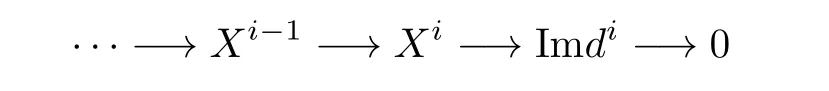
are also SCP-acyclic complexes.

Proof.SinceX∗isSCP-acyclic,in order to prove thatisSCP-acyclic,it suffices to prove that

SinceX∗is acyclic,is acyclic.Consider the following commutative diagram

By Propositions 2.4 and 2.6 of[5],we get the following two conclusions.

Proposition 2.1A complex X∗is an SCP-acyclic complex if and only ifis acyclic for anyor equivalently,

Proposition 2.2

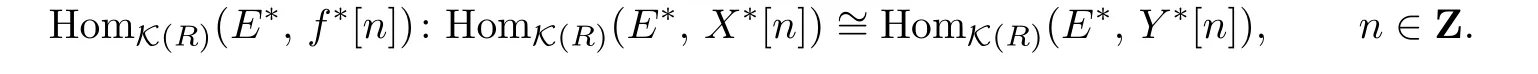
Proposition 2.3(i)

(ii)

Proof.(i)By Proposition 2.2,we have the isomorphism:

from which the assertion follows.

(ii)By(i),there exists asuch thatIt is clear thatg∗is also anSCP-quasi-isomorphism.By(i)again,there exists ansuch thatIt follows thatf∗is a homotopy equivalence.

Proposition 2.4Cone(f∗)is an SCP-acyclic complex.

Proof.By applying the cohomological functor HomK(R)(M,−)to the distinguished triangle

whereMis strongly copure projectiveR-module.We get the exact sequence

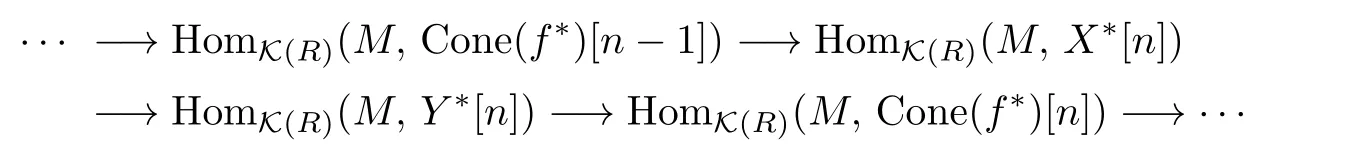
By rewriting we have the exact sequence

Sinceis anSCP-quasi-isomorphism,is an isomorphism for alln∈Z.Then

3 Homotopy Category of Strongly Copure Projective Modules

In this part,silfRis de fined as the supremum of injective lengths of fl at modules.s fl iRopis de fined as the supremum of fl at lengths of injective rightR-modules.SCPis de fined as the category of strongly copure projective modules.

Lemma 3.1Let R be a right coherent ring.ThensilfR≤s fl iRop.

Proof.The inequality is obvious if s fl iRop=∞and hence we may assume that s fl iRop=n＜∞withna positive integer.LetFbe an arbitrary fl atR-module.Consider the exact sequence

with eachIiinjective.To complete the proof,it is enough to show thatLis injective.Applying the exact functor(·)+=HomZ(−,Q/Z)on this sequence to get the exact sequence

Clearly,F+is an injective rightR-module.SinceRis right coherent,each(Ii)+is fl at by Lemma 3.14 of[6].Hence,by assumption,L+is fl at.So,by Lemma 3.14 of[6]again,Lis injective.Thus silfR≤n.

Lemma 3.2(i)Let R be a1-FC ring.Then SCP is closed under taking submodules.

Proof.(i)Let,andM′is a submodule ofM.Then we have the following exact sequence:

Applying the functor HomR(−,P)to it withPprojective,by dimension-shift,we get

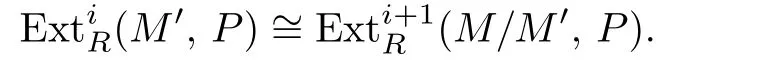
SinceRis a 1-FC ring,FP-idRR≤1.It follows from Theorem 3.8 of[7]that s fl iand silfR=silpR≤1 by Proposition 2.1 of[8]and Lemma 3.1.ThenSo

This meansM′∈SCP.

(ii)Since we have a series of exact sequences:

By dimension-shift,we get

withPprojective.SinceRis ann-FC ringIt follows from Theorem 3.8 of[7]thatand silfR=silpR≤nby Proposition 2.1 of[8].SoThenThis means

LetDbe a triangulated category.Denote by[1]the shift functor.A pair(U,V)of full subcategories ofDis called a stablet-structure inD(see[2])provided that

(1)

(2)HomD(U,V)=0.

(3)For eachX∈D,there exists a trianglewithand

A right recollement of triangulated categories(see[1])is a diagram of triangulated categories and exact functors

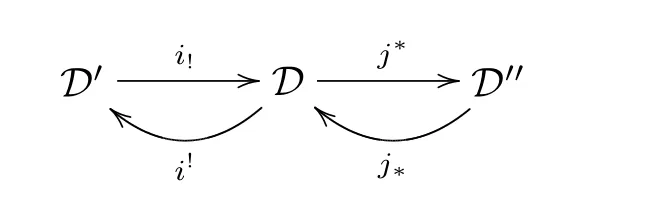
satisfying

(2)

(3)i!andj∗are full embeddings.

(4)Each objectX∈Ddetermines a distinguished triangle

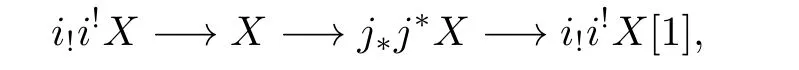
where the arrows toXand fromXare counit and unit morphisms.

LetDbe a triangulated category,and(U,V)be a stablet-structure inD.Then by[2] the canonical embeddingandhave a right adjointand a left adjoint

Lemma 3.3[9]Let D be a triangulated category with small Hom-set and C be a thick triangulated category of D.If the canonical embedding i::

De finewith∗∈{∞,−,b}to be the full subcategory ofby

Theorem 3.1Let R be an n-FC ring.Then we have the following:

(i)A pairis a stable t-structure in

(ii)The canonical embedding i!:

Proof.By Lemma 2.4 of[5],we have

where for anyE∈SCP,there existm,k∈Zsuch thatforandi＞k.Let

SinceRis ann-FC ring andis exact,it follows from Lemma 3.2 that kerBywe get.ThenLet

Thenby Lemma 2.1,and we have an exact sequence of complexes

This induces a triangle in

By the de finition of stablet-structure,we get thatis a stabletstructure inBy[2]we get that the canonical embeddingi!:has a right adjointi!:SinceSCPis closed under direct summands,it follows thatis a thick triangulated category ofHence by Lemma 3.3 we can obtain a right recollement

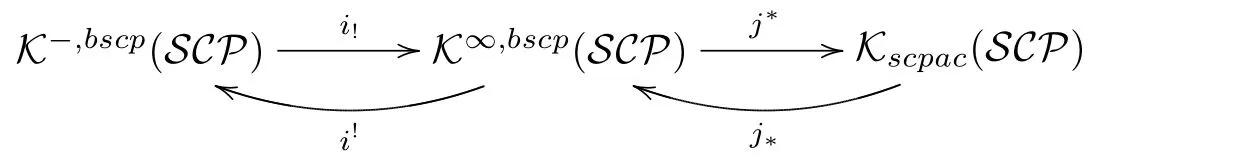
LetRbe ann-FC ring.By Theorem 3.11 of[3],every finitely presentedR-moduleMhas a proper strongly copure projective resolutionWe denoteR-mod the full subcategories consisting of finitely presented modules of all leftR-modules.

Theorem 3.2Let R be an n-FC ring.Then we have a right recollement

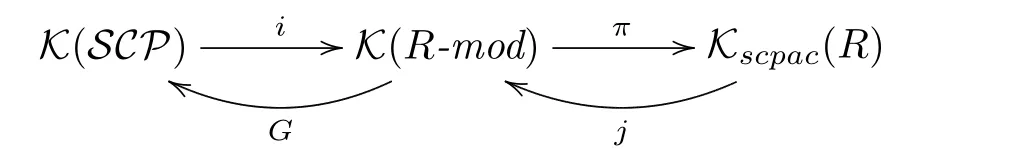
In this case,(K(SCP),Kscpac(R))is a stable t-structure in K(R-mod).

Proof.By de finition,SCPcontains all the finitely generated projective modules and is closed under direct summands.SinceRis ann-FC ring,it follows from Theorem 3.11 of [3]thatSCPis contravariantly finite subcategory ofR-mod.So every finitely presentedR-moduleMhas a proper strongly copure projective resolution

Hence by Proposition 3.5 of[10],the canonical embeddingi:has a right adjointG:By Lemma 3.3,we get a right recollement

In this case,we haveandi,jare full embeddings.Hence,for arbitraryandwe have a series of isomorphisms

Moreover,we have that each objectindetermines a distinguished triangle

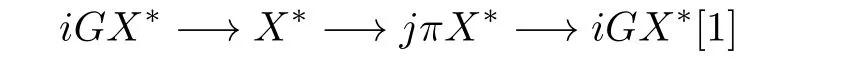
Again byiandjare full embeddings,we getandTherefore,is a stablet-structure in

[1]Beilinson A A,Bernstein J.Faisceaux Pervers.in:Deligne P eds.Proceedings of the Conference Analysis and Topology on Singular Spaces,vol.100,Ast´erisque:Luminy,1982.

[2]Miyachi J.Localization of triangulated categories and derived categories.J.Algebra,1991,141:463–483.

[3]Mao L X.Some aspects of stronglyP-projective modules and homological dimensions.Comm. Algebra,2013,41:19–33.

[4]Enochs E E,Jenda O M G.Copure injective resolutions, fl at resolvents and dimensions.Comment.Math.Univ.Carolin,1993,189:167–193.

[5]Christensen L W,Frankild A,Holm H.On gorenstein projective,injective and fl at dimensions—a functorial description with applications.J.Algebra,2006,302:231–279.

[6]Xu J.Flat covers of modules.Lecture Notes in Math.,vol.1634,Berin:Springer-Verlat,1996.

[7]Ding N Q,Chen J L.The fl at dimensions of injective modules.Manuscripta Math.,1993,78: 165–177.

[8]Emmanouil I,Talelli O.On the fl at length of injective modules.J.Lond.Math.Soc.,2011,84:408–432.

[9]Neeman A.Triangulated Categories.Annals of Mathematics Studies,vol.148,Preinceton: Princeton University Press,NJ,2001.

[10]Chen X W.Homotopy equivalences induced by balanced pairs.J.Algebra,2010,324:2718–2731.

tion:18E30,18G10

A

1674-5647(2017)03-0281-08

10.13447/j.1674-5647.2017.03.08

date:Sept.21,2016.

The NSF(11461060)of China.

E-mail address:maxin263@126.com(Ma X).