Multilinear Calderón-Zygmund Operators and Their Commutators with BMO Functions in Herz-Morrey Spaces with Variable Smoothness and Integrability

Hu Yuan-zhu and Xu Jing-shi

(School of Mathematics and Statistics,Hainan Normal University,Haikou,571158)

Multilinear Calderón-Zygmund Operators and Their Commutators with BMO Functions in Herz-Morrey Spaces with Variable Smoothness and Integrability

Hu Yuan-zhu and Xu Jing-shi*

(School of Mathematics and Statistics,Hainan Normal University,Haikou,571158)

Communicated by Ji You-qing

In this paper,we obtain that multilinear Calder´on-Zygmund operators and their commutators with BMO functions are bounded on products of Herz-Morrey spaces with variable smoothness and integrability.The vector-valued setting of multilinear Calder´on-Zygmund operators is also considered.

multilinear Calder´on-Zygmund operator,variable exponent,Herz-Morrey space,vector valued estimate

1 Introduction

Recent decades,variable exponent function spaces have been received more and more attention.This mainly began with the work of Kov´aˇcik and R´akosn´ık in 1991.In[1],Kov´aˇcik and R´akosn´ık gave fundamental properties of the variable Lebesgue and Sobolev spaces.Then some sufficient conditions were obtained for the boundedness of Hardy-Littlewood maximal operator on variable Lebesgue spaces(see[2]).After that,many function spaces with variable exponents appeared,such as Besov and Trieble-Lizorkin spaces with variable exponents,Hardy spaces with variable exponents,Morrey spaces with variable exponent,Bessel potential spaces with a variable exponent and Herz-Morrey spaces with variable exponents (see[3]–[17]).Herz-Morrey spaces are a generalization of Herz spaces.For the classical Herz spaces we refer the reader to the monograph by Luet al.[18]

Recently,linear and multilinear singular operators and their commutators are also intensively studied by a signi ficant number of authors,for instance,see[19]–[25].

In this paper we consider the boundedness of multilinear Calder´on-Zygmund singular operators,their commutators with BMO functions and their vector-valued setting in Herz-Morrey spaces with three variable exponents

2 Main Results

To state the main results of this paper,we need recall some notions firstly.

Letmbe an integer not less than 2.A multilinear operatorTis called a Calder´on-Zygmund operator if it is initially de fined on them-fold product of the Schwartz spaceS(Rn)and can be extended bounded fromtoLpfor some 1＜p1,withand for(the space of compactly supported bounded functions),supp

where the kernelKis a function inaway from the diagonaland there exist positive constantsϵ,Asuch that

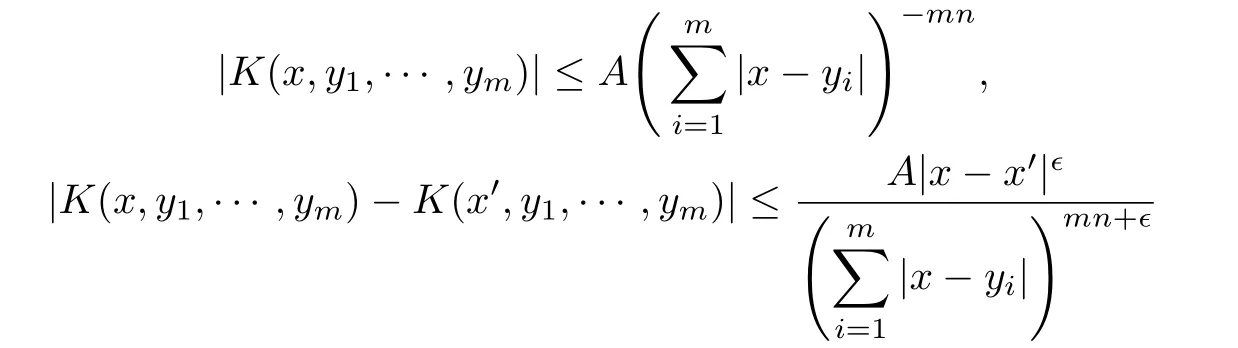
provided that

and for eachi∈{1,2,···,m},

provided that

Grafakos and Torres[26]showed that ifTis anm-linear Calder´on-Zygmund operator, thenTis bounded fromtoLqfor eachsuch thatMoreover,Grafakos and Torres[19]obtained weighted norm inequalities for multilinear Calder´on-Zygmund operators.

De finition 2.1

(i)The Lebesgue space with variable exponentis de fined by

(ii)

where and what follows,χSdenotes the characteristic function of a measurable set

is a Banach function space when equipped with the norm

LetWe denoteandThe setP(Rn)consists of allp(·)satisfyingandandconsists of allp(·) satisfyingandcan be similarly de fined as above formeans the conjugate exponent ofp(·),that means

whereBis a ball.LetB(Rn)be the set ofsuch thatMis bounded on

De finition 2.2Let α(·)be a real-valued measurable function onRn.

(i)α(·)is locally log-Hölder continuous if there exists a constant C1such that

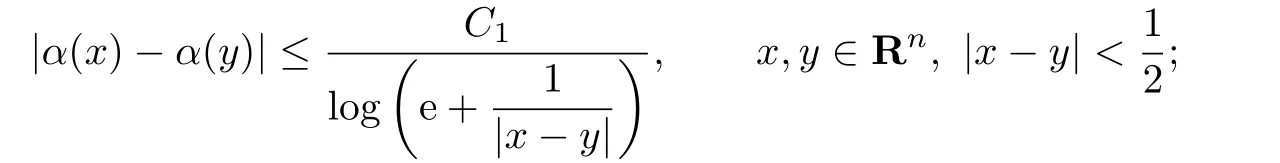
(ii)

(iii)α(·)is log-Hölder continuous at the in finity if there exists α∞∈Rsuch that

(iv)α(·)is global log-Hölder continuous if α(·)is both locally log-Hölder continuous and log-Hölder continuous at the in finity.

It is well known that(see[23]).

LetThe mixed Lebesgue-sequence spaceis de fined on sequences ofLq(·)-functions by the modular

The(quasi-)norm is de fined from this as usual:

Sinceq+＜∞,we can replace(2.1)by the simpler expression

Furthermore,ifpandqare constants,then

To give the de finitions of Herz spaces and Herz-Morrey spaces with variable exponents, we use the following notations.For eachk∈Z,we de fineFor eachandThe following spaces were firstly introduced by Izuki and Noi[27].

De finition 2.3consists of allsuch that

De finition 2.4

(i)The homogeneous Herz-Morrey spaceis de fined by

where

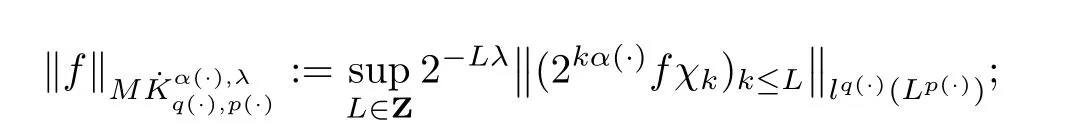
(ii)The non-homogeneous Herz-Morrey spaceis de fined by

where

Throughout this paper,Calways denote a positive constant depending on the context, whose value may be di ff erent at di ff erent occurrences.

Our main results are the following theorems.

Theorem 2.11,2,···,m}andsuch thatfor someLetfor i∈{1,2,···,m}such thatLetand0≤λi＜∞withwhereare theconstants appearing in(3.2)and(3.3)for pi(·),i∈{1,2,···,m}.Suppose thatandThen the m-linear Calder´on-Zygmund operator T is bounded on theproduct of variable exponent Herz-Morrey spaces.Moreover,

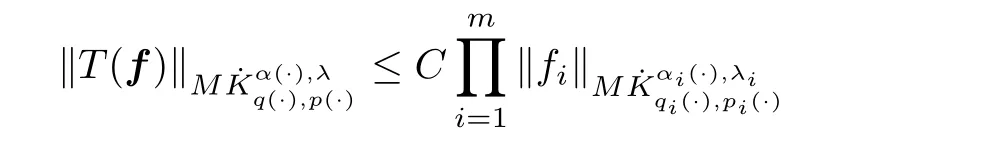
with the constant C＞0independent off.

Letλi=0.We immediately get the boundedness of the multilinear Calder´on-Zygmund integral operator on the product of variable exponent Herz spaces.

Theorem 2.21,2,···,m}andsuch thatfor some.Letfor i∈{1,2,···,m}such that.Letandwithwhereare theconstants appearing in(3.2)and(3.3)for pi(·),i∈{1,2,···,m}.Suppose thatandThen the m-linear Calder´on-Zygmund operator T is bounded on theproduct of variable exponent Herz spaces.Moreover,

with the constant C＞0independent off.

Theorem 2.3such thatfor someLetfor i∈{1,2,···,m}such thatLetandwith(3.2)and(3.3)andLetthen

with the constant C＞0independent of

with the constant C＞0independent of

Remark 2.2Here we only declare our result in the homogeneous Herz-Morrey spaces with variable exponents,but there is an analogue for the non-homogeneous Herz-Morrey spaces with variable exponents,we omit the detail here.

3 Proofs of the Main Results

For brevity,we use the notationif there exist a constantc＞0 such thatIfandwe write

To prove our results,we need the following Lemmas.

Lemma 3.1[28]0such that for all balls B inRn,

Lemma 3.2[11]0such that for all balls B inRnand all measurable subsets

and

Lemma 3.3[29]

Additionally,if α and q are log-Hölder continuous at the origin,then

here and hereafter q0:=q(0).

From Lemma 3.3,we easily have the following lemma.

Lemma 3.4Then

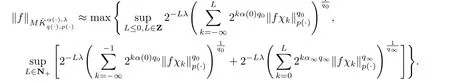
Lemma 3.6[23]for somethen the m-linear Calder´on-Zygmund operator T is bounded on the product of variable exponent Lebesgue spaces.Moreover,

with the constant C independent of

Lemma 3.7[29]Let0＜a＜1andLet{bk}k∈Zbe a sequence of positive realnumbers such thatThen the sequencesandbelong to ℓqand

with the constant C only depending on a and q.

Proof of Theorem 2.1Without loss of generality,we only consider the case thatm=2. Actually,similar procedure works for allm≥3.Write

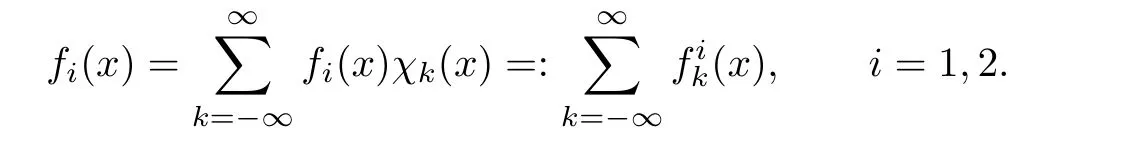
Let

Then from Lemma 3.4,we have

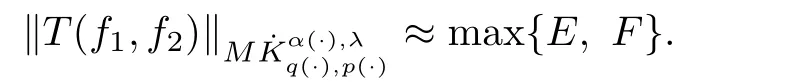
Since the estimation ofEis essentially similar to that ofF,so it suffices to prove thatFis bounded in Herz-Morrey spaces with variable exponents.It is easy to see that

where

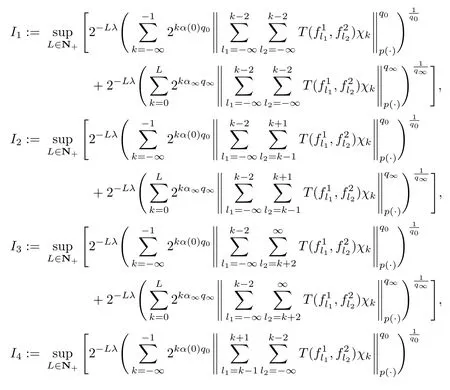
Because of the symmetry off1andf2,we see that the estimate ofI4is analogous to that ofI2,the estimate ofI7is similar to that ofI3and the estimate ofI8is similar to that ofI6.So we shall only estimateI1,I2,I3,I5,I6andI9,respectively.

(i)To estimate the term ofI1,we note thatforand

Then,forwe obtain

Applying Hölder’s inequality to the last integral,we obtain

By Lemmas 3.1 and 3.2,we have

Therefore,we arrive at the inequality

LetandandSinceit follows that

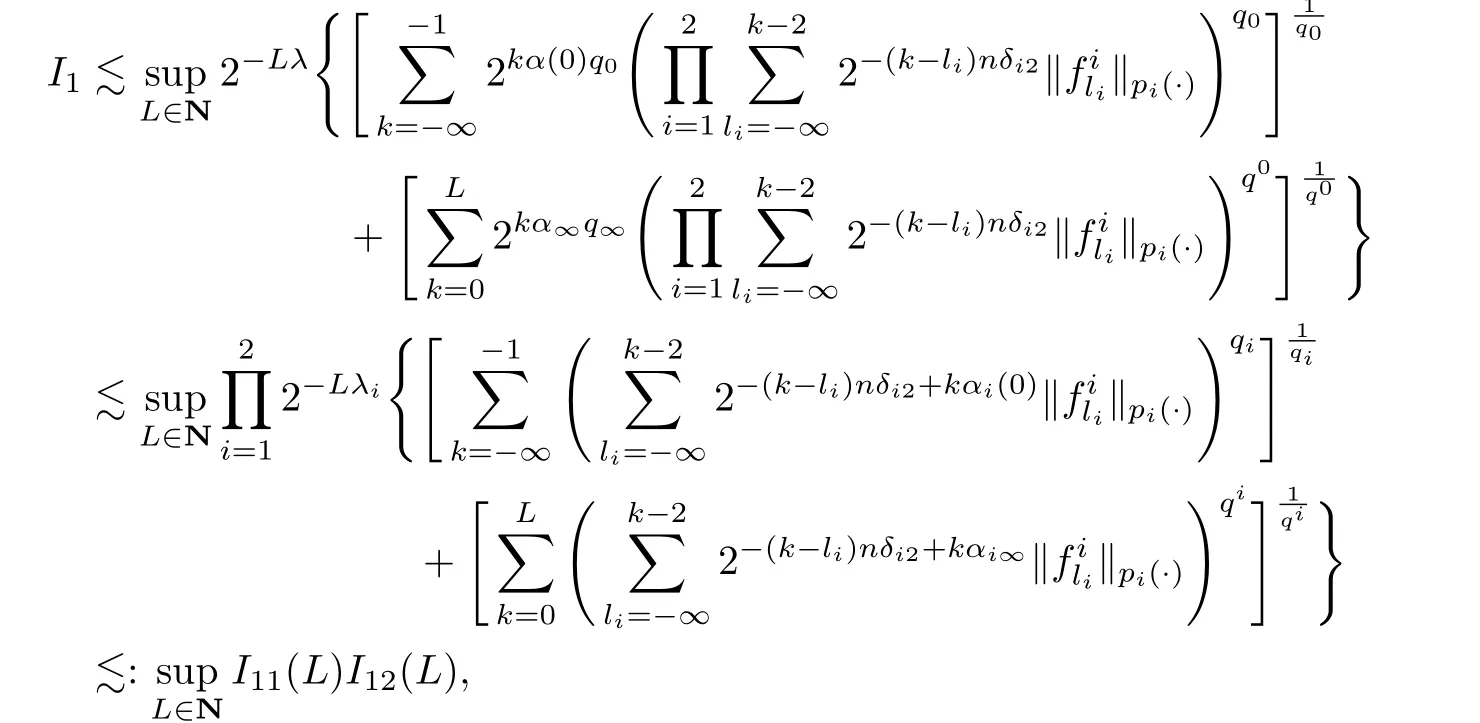
where

In the above derivation,we noticed the fact ofandand used Lemma 3.7.

(ii)To estimateI2,we haveandand then forone has

Then,forwe obtain

Applying Hölder’s inequality to the last integral,we obtain

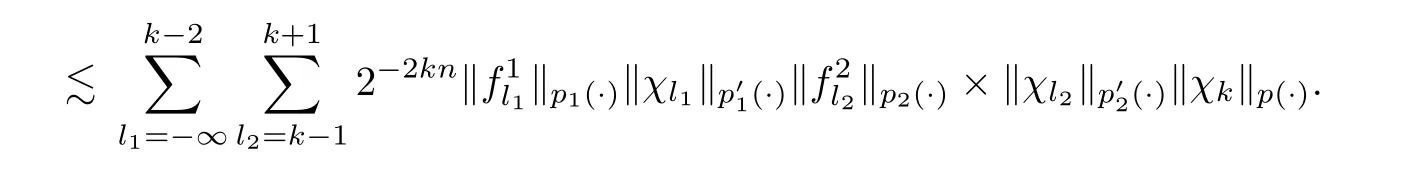
By Lemmas 3.1 and 3.2,we have

Therefore,we arrive at the inequality

Then we have

Note that

Thus we obtain

(iii)To estimateI3,forandwe have

Thus,forwe get

By Hölder’s inequality and Lemma 3.2,we have

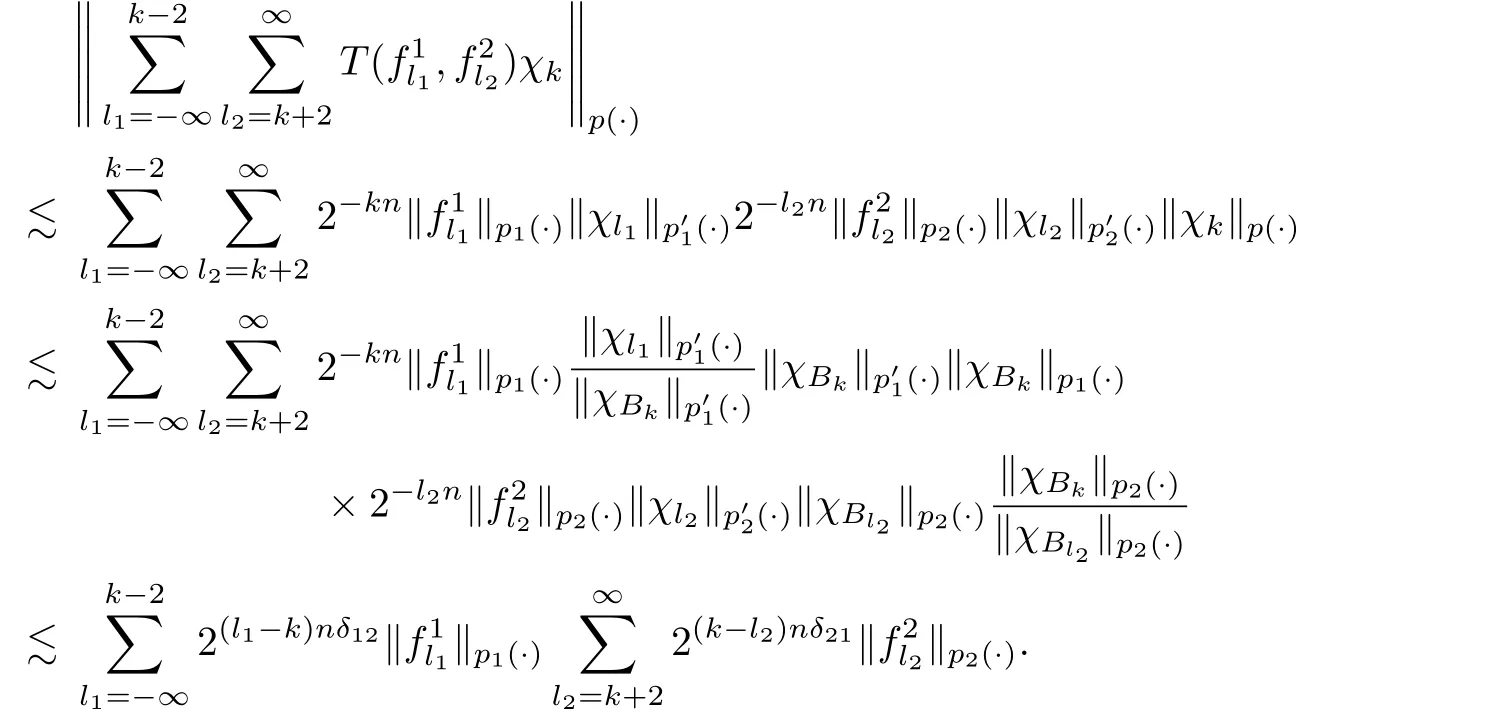
So we get

Here

Note that

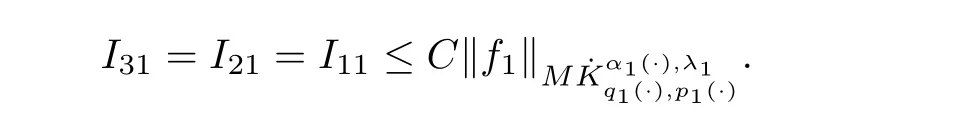
To estimatewe write

we obtain

For,whenby the fact that

we have

Forwhenby the fact thatwe have

Therefore,we get

(iv)To estimate the termI5,by Lemma 3.2,theLp(·)-boundedness ofT,we note that

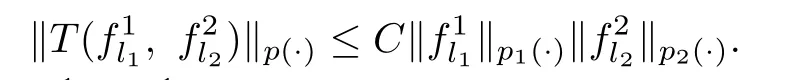
(v)To estimate the termI6,forandwe have

By Hölder’s inequality and Lemma 3.2,we obtain

Hence

here the estimate ofI61(L)is equal to that ofI22(L)andI62(L):=I32(L).Then we have

(vi)Finally,to estimate the term ofI9,we note thatl2≥k+2 andfor.Hence

Applying Hölder’s inequality to the last integral,and by Lemmas 3.2,we obtain

Thus

Since the estimates ofare similar to that ofI32(L),so we have

Combining all the estimates forIitogetheri=1,2,···,9,we get

The proof of Theorem 2.1 is completed.

Proof of Theorem 2.3In the following,we only consider 2-linear operators for simplicity. Since the set of all bounded compactly supported functions is dense in Herz-Morrey spaces with variable exponents,we letf1andf2be bounded compactly supported functions forj∈N+and write

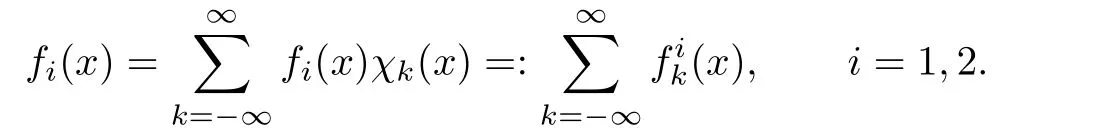
By Lemma 3.4,we get

where

We do the same estimates and calculations as in the proof of Theorem 2.1(also as the proof of Theorem 6 in[25]),then we can conclude what we want.We omit the detail here. Thus we complete the proof.

Proof of Theorem 2.4In the following,we only consider 2-linear operators for simplicity. Since the set of all bounded compactly supported functions is dense in Herz-Morrey spaceswith variable exponents,we letandbe bounded compactly supported functions forand write

By Lemma 3.4,we get

where

We do the same estimates and calculations as in the proof of Theorem 2.1,we can obtain what required.We leave the detail here.Thus we complete the proof.

[1]Kov´aˇcik O,R´akosn´ık J.On spacesLp(x)andWk,p(x).Czechoslovak Math.J.,1991,41:592–618.

[2]Nekvinda A.Hardy-Littlewood maximal operator onLp(x).Math.Inequal.Appl.,2004,7: 255–265.

[3]Almeida A,Hasanov J,Samko S.Maximal and potential operators in variable exponent Morrey spaces.Georgian Math.J.,2008,15:195–208.

[4]Almeida A,Drihem D.Maximal,potential and singular type operators on Herz spaces with variable exponts.J.Math.Anal.Appl.,2012,394:781–795.

[5]Almeida A,H¨astö P.Besov spaces with variable smoothness and integrability.J.Funct.Anal., 2010,258:1628–1655.

[6]Dong B H,Xu J S.New Herz type Besov and Triebel-Lizorkin spaces with variable exponents.J.Funct.Spaces Appl.,2012,2012,Article ID 384593,27 pages.

[7]Fu J,Xu J S.Characterizations of Morrey type Besov and Triebel-Lizorkin spaces with variable exponents.J.Math.Anal.Appl.,2011,381:280–298.

[8]Gurka P,Harjulehto P,Nekvinda A.Bessel potential spaces with variable exponent.Math. Inequal.Appl.,2007,10:661–676.

[9]Ho K P.Vector-valued singular integral operators on Morrey type spaces and variable Triebel-Lizorkin-Morrey spaces.Ann.Acad.Sci.Fenn.Math.,2012,37:375–406.

[10]Ho K P.Atomic decomposition of Hardy-Morrey spaces with variable exponents.Ann.Acad. Sci.Fenn.Math.,2015,40:31–62.

[11]Izuki M.Boundedness of vector-valued sublinear operators on Herz-Morrey spaces with variable exponent.Math.Sci.Res.J.,2009,13:243–253.

[12]Kempka H.2-Microlocal Besov and Triebel-Lizorkin spaces of variable integrability.Rev.Mat. Complut.,2009,22:227–251.

[13]Kempka H.Atomic,molecular and wavelet decomposition of generalized 2-microlocal Besov spaces.J.Funct.Spaces Appl.,2010,8:129–165.

[14]Nakai E,Sawano Y.Hardy spaces with variable exponents and generalized Campanato spaces.J.Funct.Anal.,2012,262:3665–3748.

[15]Sawano Y.Atomic decompositions of Hardy spaces with variable exponents and its application to bounded linear operators.Integral Equations Operator Theory,2013,77:123–148.

[16]Wang H,Liu Z.The Herz-type Hardy spaces with variable exponent and their applications.Taiwanese J.Math.,2012,16:1363–1389.

[17]Xu J S.Variable Besov and Triebel-Lizorkin spaces.Ann.Acad.Sci.Fenn.Math.,2008,33: 511–522.

[18]Lu S,Yang D,Hu G.Herz Type Spaces and Their Applications.Beijing:Science Press,2008.

[19]Grafakos L,Torres R.Maximal operator and weighted norm inequalities for multilinear singular integrals.Indiana Univ.Math.J.,2002,51:1261–1276.

[20]Izuki M.Boundedness of commutators on Herz spaces with variable exponents.Rend.Circ. Mat.Palermo(2),2010,59:199–213.

[21]Lian J L,Li J,Wu H X.Multilinear commutators of BMO functions and multilinear singular integrals with non-smooth kernels.Appl.Math.J.Chinese Univ.Ser.B.,2011,26:109–120.

[22]Chen D X,Mao S Z.Weighted estimates for maximal commutators of multilinear singular integrals.J.Funct.Spaces Appl.,2012,2012,Article ID 128520,20 pages.

[23]Huang A W,Xu J S.Multilinear singular integrals and commutators in variable exponent Lebesgue spaces.Appl.Math.J.Chinese Univ.Ser.B.,2010,25:69–77.

[24]Lu Y,Zhu Y P.Boundedness of Multilinear Calder´on-Zygmund Singular Operators on Morrey-Herz Spaces with variable exponents.Acta Math.Sin.,(Engl.Ser.),2014,30:1180–1194.

[25]Tang C,Wu Q,Xu J.Commutators of multilinear Calder´on-Zygmund operator and BMO functions in Herz-Morrey spaces with variable exponents.J.Funct.Spaces.,2014,2014,Article ID 162518,12 pages.

[26]Grafakos L,Torres R.Multilinear Calder´on-Zygmund theory.Adv.Math.,2002,165:124–164. [27]Izuki M,Noi T.Duality of Besov,Triebel-Lizorkin and Herz spaces with variable exponents.Rend.Circ.Mat.Palermo(2),2014,2:221–245.

[28]Izuki M.Fractional integrals on Herz-Morrey spaces with variable exponents.Hiroshima Math. J.,2010,40:343–355.

[29]Drihem D,Seghiri F.Notes on the Herz-type Hardy spaces of variable smoothness and integrability.Math.Inequal.Appl.,2016,19:145–165.

tion:42B25,42B35

A

1674-5647(2017)03-0238-21

10.13447/j.1674-5647.2017.03.05

date:March 9,2016.

The NSF(11361020)of China and the NSF(20151011)of Hainan Province.

*

.

E-mail address:1621873782@qq.com(Hu Y Z),jingshixu@126.com(Xu J S).