On C-left Hyperideals of Ordered Semihypergroups

Tang Jianand Xie Xiang-yun

(1.School of Mathematics and Statistics,Fuyang Normal College, Fuyang,Anhui,236037)

(2.School of Mathematics and Computational Science,Wuyi University, Jiangmen,Guangdong,529020)

On C-left Hyperideals of Ordered Semihypergroups

Tang Jian1and Xie Xiang-yun2,*

(1.School of Mathematics and Statistics,Fuyang Normal College, Fuyang,Anhui,236037)

(2.School of Mathematics and Computational Science,Wuyi University, Jiangmen,Guangdong,529020)

Communicated by Du Xian-kun

In this paper,the concept ofC-left hyperideals is introduced in ordered semihypergroups,and several related properties are investigated.In particular,we discuss the relationships between the greatest left hyperideals andC-left hyperideals of ordered semihypergroups.Furthermore,we introduce the concept of left bases of an ordered semihypergroup,and give out the sufficient and necessary conditions of the existence of the greatestC-left hyperideal of an ordered semihypergroup by the properties of left bases.The result aboutC-left ideals in ordered semigroups is generalized to the ordered semihypergroups.

ordered semihypergroup,C-left hyperideal,maximal left hyperideal, left base

1 Introduction

In mathematics,an ordered semigroup is a semigroup together with a partial order that is compatible with the semigroup operation.Ordered semigroups have several applications in the theory of sequential machines,formal languages,computer arithmetics and errorcorrecting codes.There are several results which have been added to the theory of ordered semigroups by several researchers.For more details,the reader is referred to[1]–[6].Inparticular,Kehayopulu[1],[3]introduced the concepts of ideals,prime ideals and weakly prime ideals of ordered semigroups,and provided some results which are similar to that in ring theory.In[4]and[6],Xieet al.de fined and studied theC-ideals andC-left ideals in ordered semigroups.

On the other hand,algebraic hyperstructures,particularly hypergroups,were introduced by Marty[7]in 1934.Later on,algebraic hyperstructures have been intensively studied,both from the theoretical points of view and especially for their applications in other fields(see [8]).One of the main reasons which attracts researchers towards algebraic hyperstructures is its unique property that in algebraic hyperstructures composition of two elements is a set,while in classical algebraic structures the composition of two elements is an element. Thus algebraic hyperstructures are a suitable generalization of classical algebraic structures. The study on the theory of semihypergroups is one of the most active subjects in algebraic hyperstructure theory.A theory of hyperstructures on ordered semigroups has been recently developed.It is worth pointing out that Heidari and Davvaz[9]applied the theory of hyperstructures to ordered semigroups and introduced the concept of ordered semihypergroups, which is a generalization of the concept of ordered semigroups.Later on,Changphas and Davvaz[10]investigated the properties of hyperideals in ordered semihypergroups in detail. In[11],Tanget al.introduced the concept of hyper filters of ordered semihypergroups,and discussed the relationships between hyper filters and completely prime hyperideals of ordered semihypergroups.As a further study of hyperideals in ordered semihypergroups,in this paper we attempt to introduce and give a detailed investigation ofC-left hyperideals of an ordered semihypergroup.Especially,we discuss the relationship between the greatest left hyperideals andC-left hyperideals of ordered semihypergroups.Furthermore,we introduce the concept of left bases of an ordered semihypergroup,and provide the sufficient and necessary conditions of the existence of the greatestC-left hyperideal of an ordered semihypergroup in terms of left bases.As an application of the results of this paper,the corresponding results of semihypergroups(without order)and ordered semigroups are also obtained by moderate modi fications.

2 Preliminaries and Some Notations

Recall that a hypergroupoid(S,◦)is a nonempty setStogether with a hyperoperation, that is a map◦:whereP∗(S)denotes the set of all the nonempty subsets ofS.The image of the pair(x,y)is denoted byx◦y.IfandA,Bare nonempty subsets ofS,thenA◦Bis de fined by

AlsoA◦xis used forandx◦AforGenerally,the singletonis identi fied by its elementx.

We say that a hypergroupoid(S,◦)is a semihypergroup if the hyperoperationisassociative,that is,

for allx,y,z∈S(see[12]).We now recall the notion of ordered semihypergroups from[9].

De finition 2.1An algebraic hyperstructure(S,◦,≤)is called an ordered semihypergroup(also called po-semihypergroup in[9]),if(S,◦)is a semihypergroup and(S,≤)is a partially ordered set such that:for any x,y,a∈S,x≤y implies a◦x≤a◦y and x◦a≤y◦a.Here, if A,B∈P∗(S),then we say that A≤B if for every a∈A there exists b∈B such that a≤b.In particular,ifthen we write a≤B instead of{a}≤B.

Clearly,every ordered semigroup can be regarded as an ordered semihypergroup.Also see[11].Throughout this paper,unless otherwise mentioned,Sdenotes an ordered semihypergroup.

(1)(resp.and

(2)Ifwithb∈S,thenb∈A.

IfAis both a left and a right hyperideal ofS,then it is called a hyperideal ofS(see[9]).

LetSbe an ordered semihypergroup.Forwe de fine

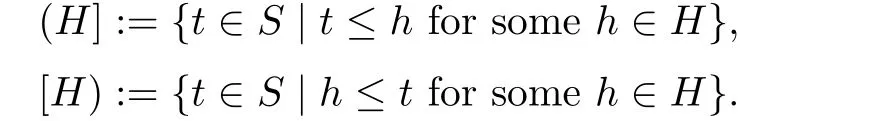
Forwe writeinstead ofrespectively.Forthe intersection of all left hyperideals ofScontainingAis called the principal left hyperideal ofSgenerated byA,denoted byL(A).One can easily prove that

Lemma 2.1Let S be an ordered semihypergroup.Then the following statements hold:

(1)

(2)

(4)For every left hyperideal T of S,we have

(5)

Proof.Straightforward.

Proof.The proof is straightforward veri fication,and hence we omit the details.

LetSbe an ordered semihypergroup.A left hyperidealLofSis called proper ifis called left simple if it has no proper left hyperideals.A proper left hyperidealLofSis called maximal,ifTis a left hyperideal ofSsuch thatthen we haveEquivalently,if for any proper left hyperidealTofSsuch thatthen we haveA proper left hyperidealLofSis called greatest if,for any left hyperidealTofS,we have

Lemma 2.3Let S be an ordered semihypergroup and L a left hyperideal of S.Then the following statements are equivalent:

(1)L is maximal;

(2)

Proof.(1)⇒(2).LetLbe a maximal left hyperideal ofS.Then,for anya∈SL,

By Lemma 2.2,is a left hyperideal ofS.Also,sinceLis maximal,we have

(2)⇒(1).Suppose thatTis a left hyperideal ofSsuch thatThen there exists anand thus

Hence we have

By hypothesis,we have

and thusT=S.Therefore,Lis maximal.

LetSbe an ordered semihypergroup.Then we de fine an equivalence relationonSas follows:

We denote theL-class containingabyLaand assign a partial order relationon theL-classes as follows:

Lemma 2.4Let S be an ordered semihypergroup andThen the following statements are equivalent:

(1)L is a maximal left hyperideal of S;

(2)

Proof.We first show thatis anL-class.In fact,leta,bbe arbitrary elements ofIfthen,clearly,By Lemma 2.2,is a left hyperideal ofS.By hypothesis,It thus implies thatwhich is a contradiction. HenceSimilarly,it can be shown thatThusOn the other hand,letIt is not difficult to show thatfor anyWe have thusshown thatis anL-class,denoted it byLa.Furthermore,if there exists anL-classLcsuch thatthenwhich implies thati.e.,Thus

which is a contradiction.Therefore,s a maximalL-class ofS.

Thus,

which is a contradiction.It thus follows thatLis a maximal left hyperideal ofS.

The reader is referred to[8]for notation and terminology not de fined in this paper.

3 C-left Hyperideals of Ordered Semihypergroups

In this section,we de fine and study theC-left hyperideals of ordered semihypergroups. In particular,we discuss the relationship between the greatest left hyperideals andC-left hyperideals of ordered semihypergroups.

De finition 3.1A proper left hyperideal L of an ordered semihypergroup S is called a C-left hyperideal of S if

In what follows,we denote bythe minimum ofxandy,andZ+the set of all positive integers.

Example 3.1Letwith the hyperoperationonSde fine by

ThenSis a semihypergroup.Furthermore,we de fine the order relation“≤”onSas follows:

It is easy to check thatSis an ordered semihypergroup.Clearly,the following subset ofS

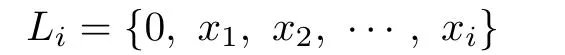
is a left hyperideal ofSfor anyandLiis aC-left hyperideal ofSsince

Theorem 3.1Let S be a commutative ordered semihypergroup.If S is not left simple, then S contains at least one C-left hyperideal of S.

Proof.LetTbe any proper left hyperideal ofS.Then

If we denote

then,sinceSis commutative,Lis a left hyperideal ofS,and

Furthermore,Lis aC-left hyperideal ofSsince

Example 3.2We consider the setwith the following hyperoperationand the order

We give the covering relationand the figure ofSas follows:

Furthermore,let

By Theorem 3.1,L1is aC-left hyperideal ofS.

ForC-left hyperideals of an ordered semihypergroup,we have the following properties.

Proposition 3.1Let S be an ordered semihypergroup.If S contains two di ff erent proper left hyperideals L1and L2

Proof.LetThen

HenceL1andL2are notC-left hyperideals ofS.Indeed,ifL1is aC-left hyperideal ofS, then

Sincewe havewhich is impossible.ThusL1is not aC-left hyperideal ofS.In a similar way,we can show thatL2is also not aC-left hyperideal ofS.

Corollary 3.1If an ordered semihypergroup S contains at least two maximal left hyperideals, then any maximal left hyperideal of S is not a C-left hyperideal of S.

Proof.LetM1andM2be two di ff erent maximal left hyperideals ofS.Then

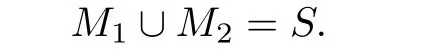
Thus,by Proposition 3.1,M1andM2are notC-left hyperideals ofS.

Proposition 3.2Let L be a maximal left hyperideal of an ordered semihypergroup S.If K is a C-left hyperideal of S,then

Proof.By Lemma 2.2,is a left hyperideal ofS.Clearly,thenIfthen,sinceLis maximal,and thus.Hence

Proposition 3.3Let S be an ordered semihypergroup.If L1and L2are two C-left hyperideals of S,thenis a C-left hyperideal of S.

Proof.We show that if

then

In fact,letThen

implies that there exists ansuch thatNext,there are two cases to be considered.

Case 1.Ifthen

Case 2.LetThen

So there exists asuch thatThen we claim thatbdoes not belong toL1.Otherwise,we would have

which is a contradiction.Thereforeand,which implies that

Thus we have

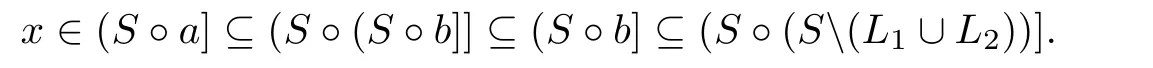
Hence

Similarly,we can prove that

Therefore,

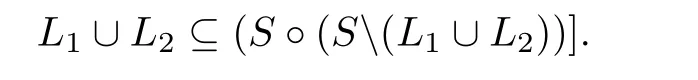
Proposition 3.4Let S be an ordered semihypergroup.If L1and L2are two C-left hyperideals of S,thenis a C-left hyperideal of S.

Proof.From the relationwe have

Therefore,is aC-left hyperideal ofS.

If we consider the empty set∅as aC-left hyperideal,then,by Propositions 3.3 and 3.4, we immediately obtain the following corollary:

Corollary 3.2The set of all C-left hyperideals of an ordered semihypergroup S is a sublattice of the lattice of all left hyperideals of S.

Proposition 3.5Let S be an ordered semihypergroup.If S contains a maximal left hyperideal L and L is a C-left hyperideal of S,thenfor all a∈SL.

Proof.Assume thatLis a maximal left hyperideal ofS.Then,by Lemma 2.3,for allIfthenLis not aC-left hyperideal ofSby Proposition 3.1.

In the following,we discuss the relationship between the greatest left hyperideal andC-left hyperideal of an ordered semihypergroup.

Proposition 3.6Let S be an ordered semihypergroup containing only one maximal left hyperideal L.If L is a C-left hyperideal of S,then L is the greatest left hyperideal of S.

Proof.Suppose thatLis a maximal left hyperideal ofS,and letKbe a left hyperideal ofSsuch thatThenand thusBy Proposition 3.1,Lis not aC-left hyperideal ofS.This is a contradiction.Therefore,Lis the greatest left hyperideal ofS.

Proposition 3.7Let S be an ordered semihypergroup.If S contains the greatest left hyperideal L∗,then L∗is a C-left hyperideal of S or there exists ansuch that

Proof.LetL∗be the greatest left hyperideal ofS.Then,and thusBy Lemma 2.1(5)is a left hyperideal ofS.SinceL∗is the greatest left hyperideal ofS,we have

or

IfL∗is not aC-left hyperideal ofS,then

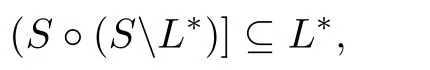
and we have

HenceWe first show thatis a left hyperideal ofS.Ifandthen we haveIn fact,if there exists asuch thatthen

that is,Impossible.Thus

Furthermore,letandwithThen.Otherwise,ifthenThuswhich is a contradiction.Thus,is a left hyperideal ofS.Also,sinceL∗is the greatest left hyperideal ofS,we have

It is well known that a semihypergroupSendowed with the equality relation

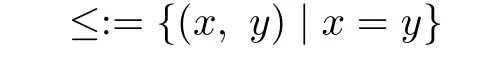
is an ordered semihypergroup.As an application of Propositions 3.6 and 3.7,we have the following theorem.

Theorem 3.2Let S be a semihypergroup and L a maximal left hyperideal of S.Then L is a C-left hyperideal of S if and only if L is the greatest left hyperideal of S.

Proof.⇒.By Proposition 3.6,the result is obvious.

⇐.LetLbe the greatest left hyperideal ofS.Then,by Proposition 3.7,there exists ansuch thatorLis aC-left hyperideal ofS.Now we show that if,thenLis also aC-left hyperideal ofS.In fact,sinceSis a semihypergroup,we haveFrom the proof of Proposition 3.7,we notice thatis a left hyperideal ofS,and thusis a maximal left hyperideal ofS.Consequently,Sinceis a left hyperideal ofSandwe have

On the other hand,and(since,so

Thus

In other words,Lis aC-left hyperideal ofS.

Theorem 3.3Let S be an ordered semihypergroup which satis fies just one of the following conditions:

(1)S contains the greatest left hyperideal L∗and it is a C-left hyperideal;

(2)

Then every proper left hyperideal of S is a C-left hyperideal.

Proof.LetLbe any proper left hyperideal ofS.Assume that the condition(1)holds. Then,and we haveThus

which implies thatLis aC-left hyperideal ofS.

Let(2)be satis fied.Ifthenwhich implies that there exists asuch that

It is obvious thatSince

we havefor someWe show thatIndeed,ifthen

which is a contradiction.Thus,we have

from which we deduce that

Therefore,Lis aC-left hyperideal ofS.

Theorem 3.4Let every proper left hyperideal of an ordered semigroup S be a C-left hyperideal.Then just one of the following conditions holds:

(1)S contains the greatest left hyperideal L∗;

(2)(b)

Proof.We first show that if every proper left hyperideal ofSis aC-left hyperideal,thenScannot contain two di ff erent maximalL-classes.Indeed,ifLcandLdare maximalL-classes andthen,by Lemma 2.4,andare two di ff erent maximal left hyperideals ofS,and none of them areC-left hyperideals ofSby Corollary 3.1.This is a contradiction. Thus there are two cases are considered:

Case 1.IfScontains just one maximalL-classLc,thenis again a maximal left hyperideal ofS,moreover,it is aC-left hyperideal.By Proposition 3.6,we have

Case 2.Suppose thatSdoes not contain maximalL-classes.First we show thatIfthen for anyIn fact,ifthenLyis amaximalL-class ofS,which is a contradiction.By assumption,is aC-left hyperideal ofS,i.e.,

Thus,

which is impossible.Therefore,

Furthermore,letLbe any proper left hyperideal ofS.Then,by hypothesis,

LetThen there exists asuch thatThis implies

SinceSdoes not contain maximalL-classes,we haveMoreover,since

Theorem 3.5Let S be an ordered semihypergroup.If every principal left hyperideal of S is a C-left hyperideal of S,then S does not contain maximal left hyperideals.

Proof.LetLabe anL-class ofS.ThenL(a)/=SsinceSis not aC-left hyperideal ofS. By hypothesis,

Thus there exists asuch thatfor someHence

Therefore,Lais not a maximalL-class ofS.By Lemma 2.4,Sdoes not contain maximal left hyperideals.

4 Left Bases of Ordered Semihypergroups

In the current section we introduce the concept of left bases of ordered semihypergroups, and provide the sufficient and necessary conditions of the existence of the greatestC-left hyperideal of an ordered semihypergroup in terms of left bases.

De finition 4.1Let S be an ordered semihypergroup andA is called a left base of S if the following conditions are satis fied:

(1)S=L(A);

(2)

In the following,we give an equivalent characterization of left bases of ordered semihypergroups.

Theorem 4.1Let S be an ordered semihypergroup andThen A is a left base of S if and only if the following conditions are satis fied:

(1)For any a∈S,there exists a b∈A such that

(2)For any a1

Proof.⇒.(1)Suppose thatAis a left base ofS.Then

and thus for anya∈S,there existsuch thatorIfa≤b1, then,clearly,

LetWe claim thatTo prove our claim,let

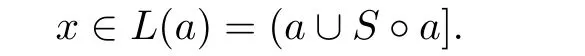
Thenx≤aorfor somey∈S.Thus

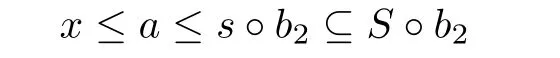
or

It implies that

Hence

(2)Letbe such that

Then

and we haveAssume thatLetSince,it can be easily shown that

Also,sinceAis a left base ofS,we haveand thusBy hypothesis,B=A,which is impossible.

⇐.Assume that the conditions(1)and(2)hold.By(1),we have

It implies thatFurthermore,suppose that there existsB⊂Asuch that

LetThen there existsuch thata≤b1orand thus

or

i.e.,orBy(2),we haveorThis is impossible.

Remark 4.1IfAis a left base of an ordered semihypergroupS,then for anya∈A, there exists a maximalL-classLsuch thata∈L,and there exists unique one element ofAin every maximalL-class.

De finition 4.2An ordered semihypergroup S is called C-left simple if it has no C-left hyperideals.

Theorem 4.2Let S be an ordered semihypergroup and not C-left simple.If there exists a left base of S,then there exists the greatest C-left hyperidealof S and in this case,

whereis the intersection of all maximal left hyperideals of S.

Proof.LetAbe a left base ofS.By Remark 4.1 and Lemma 2.4,is the set of all maximal left hyperideals ofS.By Proposition 3.2,allC-left hyperideals ofSare contained in every maximal left hyperideal ofS.SinceSis notC-left simple,we haveHence

Put

By Lemma 2.2,is a left hyperideal ofS.For anythere exists ac∈Ssuch thatSince

we havec≤bfor someorand thus

which implies thatis aC-left hyperideal ofS.

Furthermore,letKbe aC-left hyperideal ofS.ThenKis contained in every maximal left hyperideal ofSby Proposition 3.2,and thusAlso,

Hence

Therefore,is the greatestC-left hyperideal ofS.

For the converse of the above theorem,we have the following theorem.

Theorem 4.3Let S be an ordered semihypergroup which contains the greatest C-left hyperidealIfand any two elements inare incomparable,then there exists a left base of S.

Proof.Notice that any left hyperideal of an ordered semihypergroupSis a union ofL-classes.Ifthenis a union ofL-classes.Taking a representative subsetBofL-classes inLet

It is clear thatWe show thatAis a left base ofS.In fact,

(1)For anyifthen there existssuch thatLetThen

If

then there exists asuch thatThus

If

then there exists asuch thatandfor somea∈A.Thus

(2)Letsuch thatThena1=a2.Indeed,since eitherorwe need to consider the following two cases:

Case 1.Ifthen there exists ab∈Ssuch thatIfthen

and thusL(a1)is aC-left hyperideal ofS.Sinceis the greatestC-left hyperideal ofS, we havewhich implies thatImpossible.Hence

and we haveb≤a1orb≤s◦a1for somes∈S.Therefore,

i.e.,

Now,letfor somea2∈A.Then

and we have

Ifthen

and thusL(a1)is aC-left hyperideal ofS.Sinceis the greatestC-left hyperideal ofS, we have

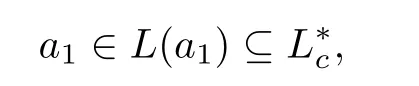
which is impossible.Henceand we obtain thatOn the other hand,

and thusHencea1=a2.

Case 2.LetIf there exists ana2∈Asuch thatthen

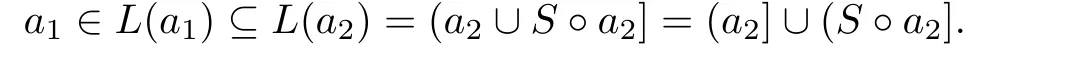
Sincewe haveIfthen

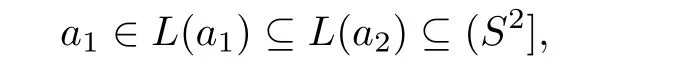
which is a contradiction.ThusandAlso,since any two elements inare incomparable,we havea1=a2.

By Theorem 4.1,Ais a left base ofS.The proof is completed.

In the above theorem,ifSis a semihypergroup(without order),then,clearly,any two elements inare incomparable.From Theorems 4.2 and 4.3,we immediately obtain the following corollary:

Corollary 4.1Let S be a semihypergroup and not C-left simple.Then S contains the greatest C-left hyperideal if and only if there exists a left base of S.

[1]Kehayopulu N.On weakly prime ideals in ordered semigroups.Math.Japon.,1990,35(6): 1051–1056.

[2]Kehayopulu N.Note on Green’s relations in ordered semigroups.Math.Japon.,1991,36(2): 211–214.

[3]Kehayopulu N.On prime,weakly prime ideals in ordered semigroups.Semigroup Forum,1992,44(1):341–346.

[4]Wu M F,Xie X Y.OnC-left ideals in ordered semigroups(in Chinese).J.Wuyi Univ.,1995,9(1):43–46.

[5]Xie X Y.On regular,strongly regular congruences on ordered semigroups.Semigroup Forum, 2000,61(2):159–178.

[6]Xie X Y,Guo X J.OnC-left ideals in ordered semigroups(in Chinese).Acta Mathematica Sinica,Chinese Series,1997,40(6):861–866.

[7]Marty F.Sur une generalization de la notion de group,8th Congress Mathematics Scandenaves, Stockholm,1934,pp.45–49.

[8]Corsini P,Leoreanu V.Applications of Hyperstructure Theory,Advances in Mathematics. Dordrecht:Kluwer Academic Publishers,2003.

[9]Heidari D,Davvaz B.On ordered hyperstructures.Politehn.Univ.Bucharest Sci.Bull.Ser. A Appl.Math.Phys.,2011,73(2):85–96.

[10]Changphas T,Davvaz B.Properties of hyperideals in ordered semihypergroups.Ital.J.Pure Appl.Math.,2014,33:425–432.

[11]Tang J,Davvaz B,Luo Y F.Hyper filters and fuzzy hyper filters of ordered semihypergroups.J.Intell.Fuzzy Systems,2015,29(1):75–84.

[12]Corsini P.Prolegomena of Hypergroup Theory.Italy:Aviani Editore Publisher,1993.

tion:20N20,06F05

A

1674-5647(2017)03-0223-15

10.13447/j.1674-5647.2017.03.04

date:Feb.25,2016.

The NSF(11271040,11361027)of China,the Key Project(2014KZDXM055)of Department of Education of Guangdong Province,the University Natural Science Project(KJ2015A161)of Anhui Province and the NSF(2014A030313625)of Guangdong Province.

*

.

E-mail address:tangjian0901@126.com(Tang J),xyxie@wyu.edu.cn(Xie X Y).