Boundedness of Fractional Integrals with a Rough Kernel on the Product Triebel-Lizorkin Spaces

Zhang Hui-hui,Yu Xiaoand Xiang Zhong-Qi

(Department of Mathematics,Shangrao Normal University,Shangrao,Jiangxi,334001)

Boundedness of Fractional Integrals with a Rough Kernel on the Product Triebel-Lizorkin Spaces

Zhang Hui-hui,Yu Xiao*and Xiang Zhong-Qi

(Department of Mathematics,Shangrao Normal University,Shangrao,Jiangxi,334001)

Communicated by Ji You-qing

By using the Littlewood-Paley decomposition and the interpolation theory,we prove the boundedness of fractional integral on the product Triebel-Lizorkin spaces with a rough kernel related to the product block spaces.

fractional integral,block space,Triebel-Lizorkin space,product space

1 Introduction and Main Results

LetSN−1be the unit sphere inRN,N≥2,with the normalized Lebesgue measure dσ=De fineandSuppose that a functionbelongs towithn,m≥2 and satis fies the following two conditions:

Then the singular integral operatorTΩ,Ion the product domain is de fined by

For the study ofTΩ,I,one may see[1]–[2]for the boundedness ofTΩ,Iwithor[3]–[5]with

De finition 1.1[6]Fora q-block on

(i)supp(b)⊂Q,where Q is an interval on

Then the de finition of the block spaceon the product domain is

where the in fimum is taken over all q-block decompositions of Ω.

Jiang and Lu[6]proved the following theorem.

Theorem 1.1[6]1and ν≥1.Thenthe operator TΩ,Iis bounded onfor m≥2and n≥2.

However,the proof of Theorem 1.1 mainly based on the Plancherel Theorem.By using some basic ideas from[7],Fanet al.[8]improved Theorem 1.1 and they proved the following result.

Theorem 1.2[8]

On the other hand,the theory of fractional integral operator also plays important roles in harmonic analysis and PDE.Denotewithand

Suppose that a functionbelongs toand only satis fies(1.1),then the fractional integral operatorTΩ,αon the product domain is de fined by

For the one parameter case,the study of singular integral and fractional integral operators with a rough kernel related to block space can be found in[9]–[11]etc.for more details. Recently,Yu and Lu[12]proved the boundedness of the fractional integral operator on the homogeneous Triebel-Lizorkin space with a rough kernel related to block spaces in the one parameter case.Motivated by the above backgrounds,we give the boundedness ofon the homogeneous product Triebel-Lizorkin spacewithand the de finition ofwill be given in Section 2.

Theorem 1.3ForletandDenoteandthen there exists a constant C is independent of f such that

2 Block Space and Triebel-Lizorkin Space on the Product Domains

In this section,we give some properties of the block space and the de finition of the Triebel-Lizorkin spaces on the product domains.

2.1 Block Space on the Product Domains

In order to study the convergence of Fourier series,Taibleson and Weiss[13]introduced the method of block decomposition for functions.Later,the block decomposition for functions in harmonic analysis was studied by many authors(see,e.g.,[14]and[15]).For more information and background about the block spaces,one may read the survey paper[16]or the survey book[17].

Recall the de finition ofin Section 1.We would like to mention that Jiang and Lu[6]also gave the following relationship of the block spaces on

2.2 Triebel-Lizorkin Space on the Product Domains

De finition 2.1[18],[19]Fix two radial functionsSuppose that Φ1and Φ2satisfy the following two conditions:

1and Φ2satisfy

From[18]and[19],we know that the dual space ofis

3 Some Lemmas

In this section,we give some lemmas and notations which will be very useful throughout this paper.Without loss of generality,we only consider the casen＞2 andm＞2.As the casem=2 orn=2 can be treated in a similar but easier way.

Forwe may decomposeby

where eachis anr-block onThen we denote

Thus,we have

De fineby

Moreover,we de fine

Thus,if we denote

then it is easy to check

Next,we are going to prove the following lemmas about

Lemma 3.1For the fourier transform ofthere is

Proof.By the de finition ofwe have

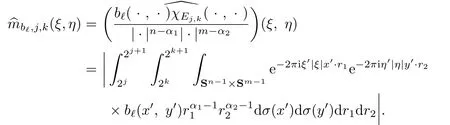
Thus,the proof of Lemma 3.1 is completed.

If we denote

then we have

Lemma 3.2Another estimate ofis

Proof.By the de finition ofFℓ,it is easy to see

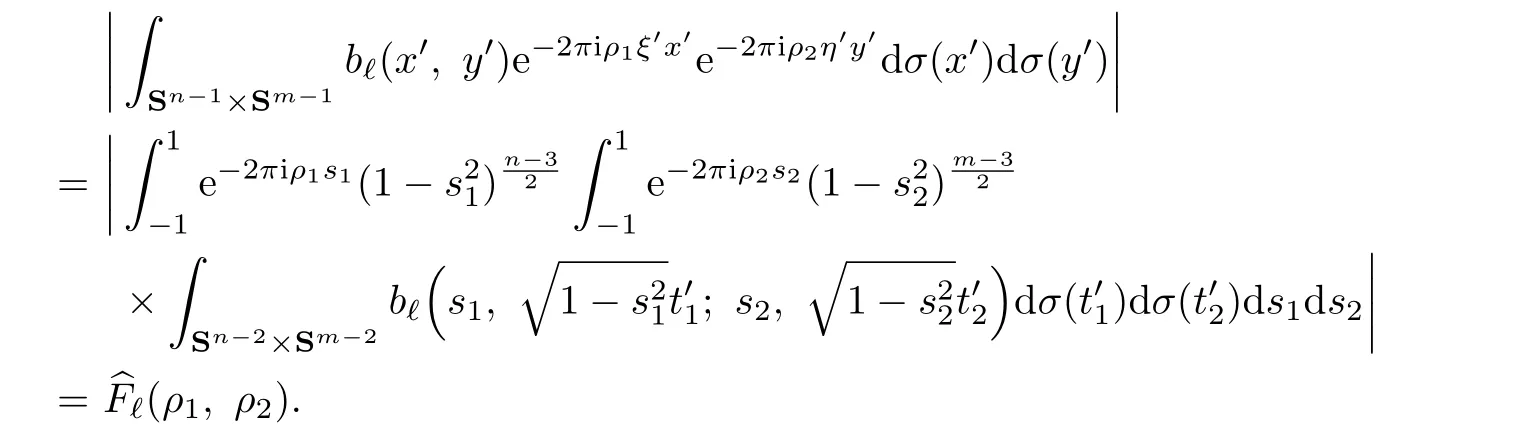
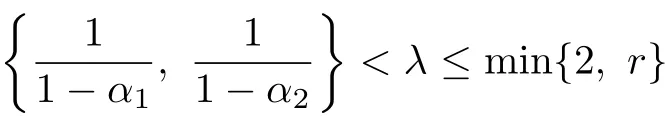
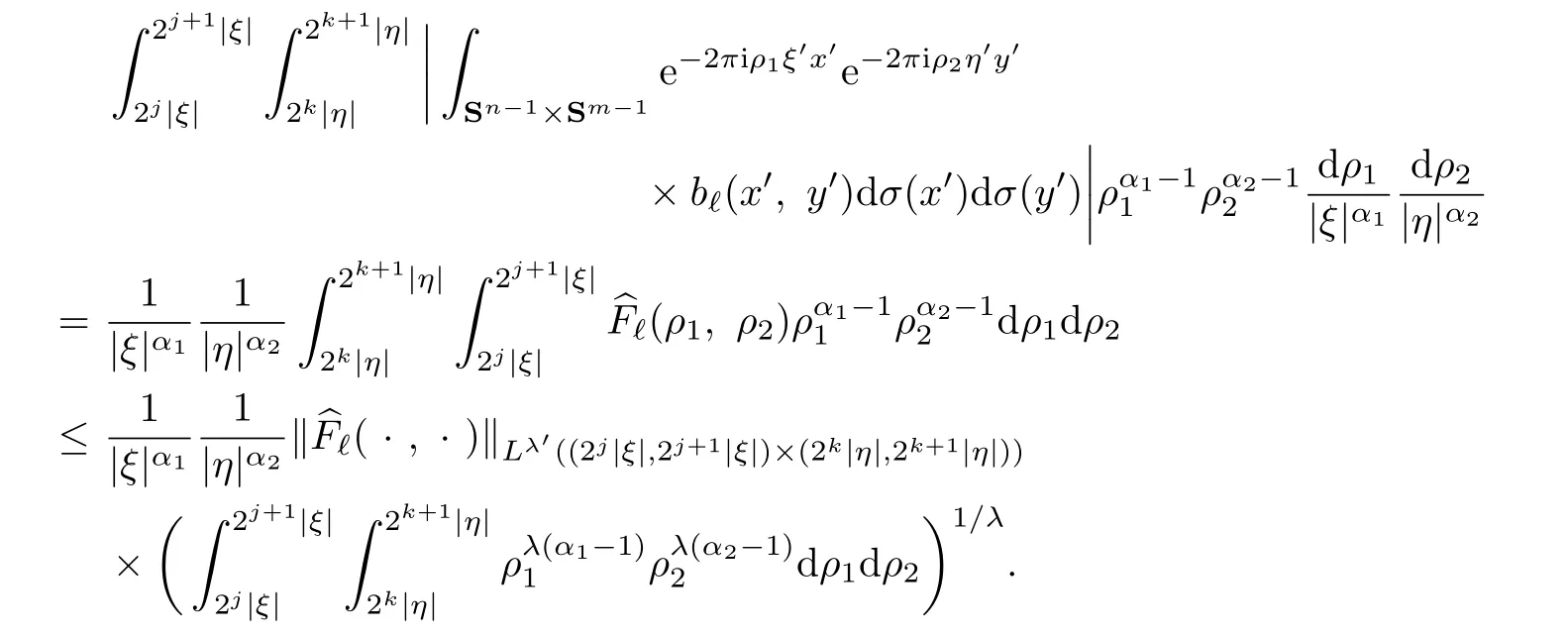
Note the following fact

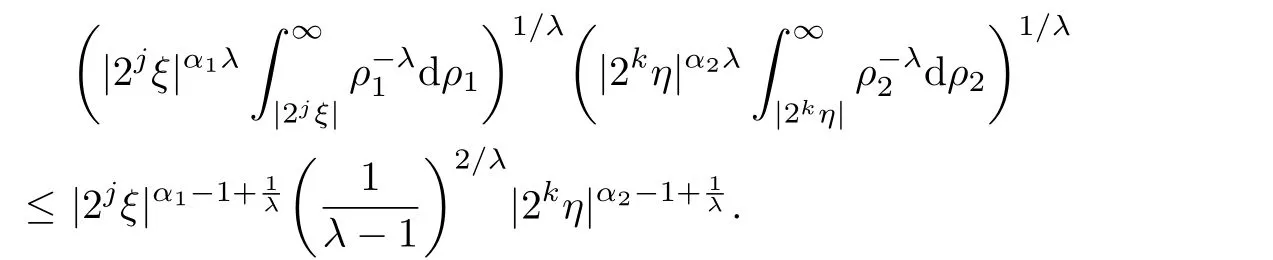
Thus,by the Hausdor ff-Young inequality,one has

which implies Lemma 3.2.

Using Lemma 3.2,we may further get

Lemma 3.3Another estimate ofis

Proof.By Lemma 3.2,we have

By the Minkowski inequality and the de finition ofmbℓ,j,k,we have

Lemma 3.4For any f∈Lp,one has

Proof.Using the Minkowski inequality and the de finition ofwe have

Lettingandbe the same as in the de finition ofand adopting some ideas from[7]–[8]and[20],we may decomposeas

Moreover,we have

Lemma 3.5For the estimates ofone has

where Lj,kis de fined by

Proof.Using the Hölder’s inequality,we obtain

as

Then,it is easy to see

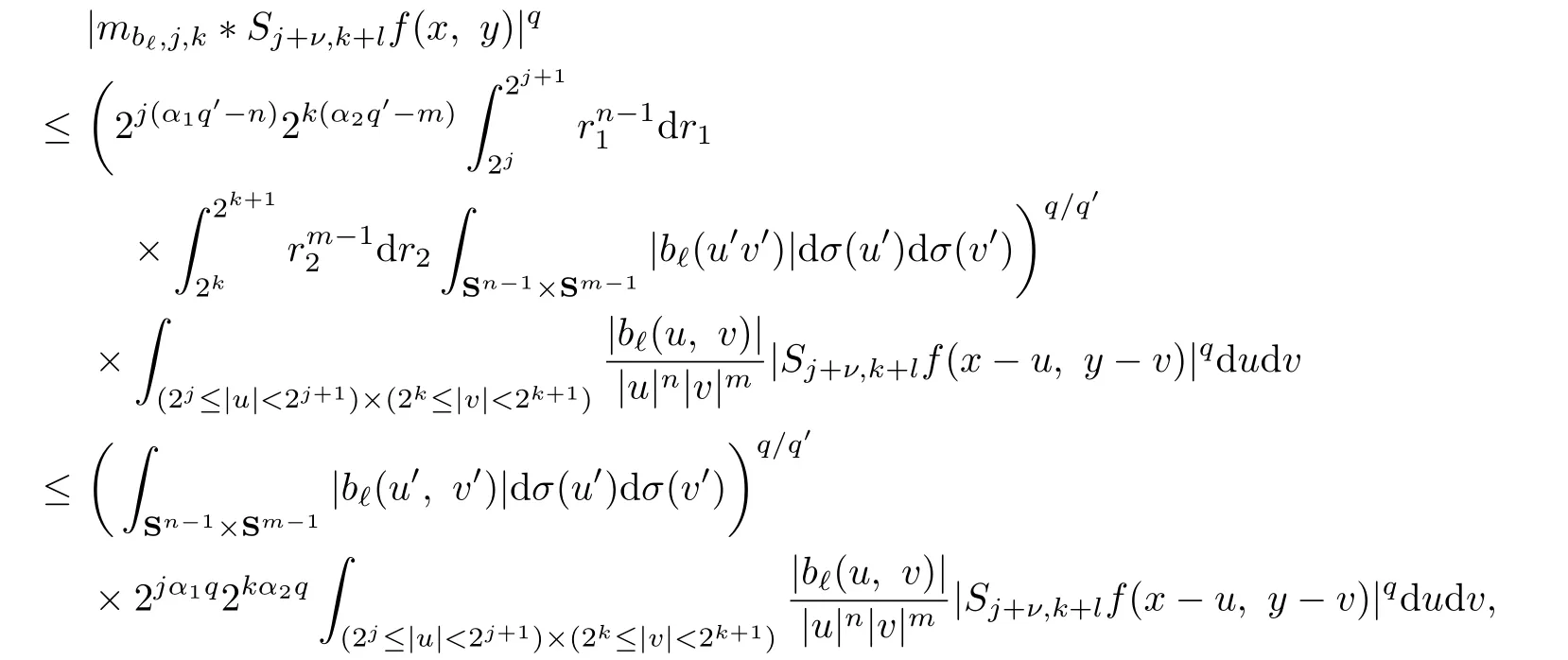
which implies Lemma 3.5.

4 Proof of the Main Results

By(iii)in Subsection 2.1,it suffices to consider the caseFrom(3.1),we have

whereis the dual operator of

For anywe have

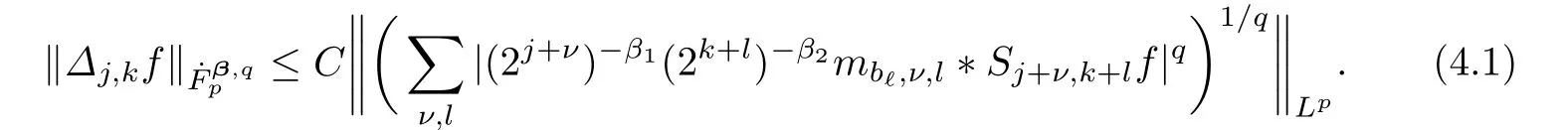
Next,we estimateby using(4.1)for di ff erent pairs(p,q).

4.1 The Casep=q=2

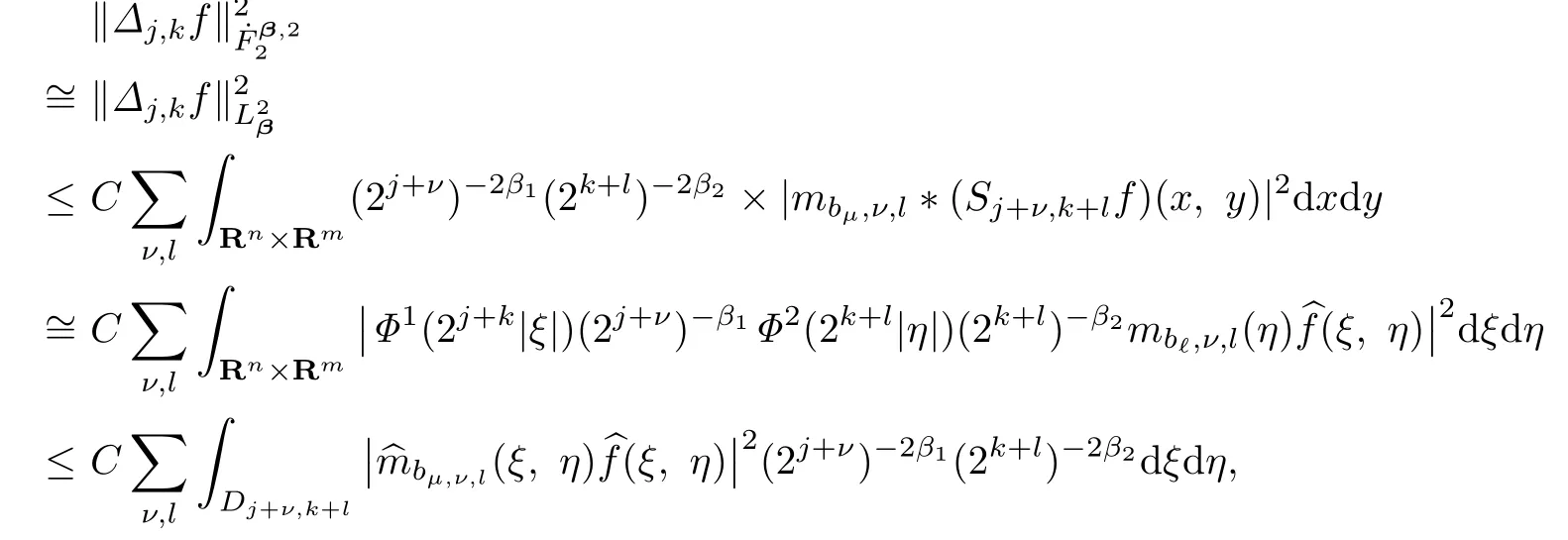
whereis de fined by

For the casej≥0 andk≥0,by using Lemma 3.1,the factandonwe get

Thus,we have

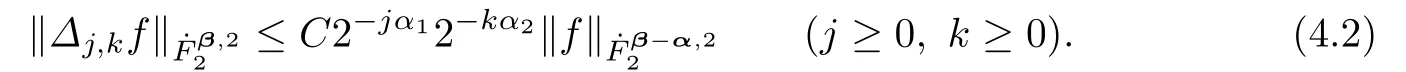
For the casej＜0 andk＜0,by using Lemma 3.3,we obtain

which implies

For the casej≥0 andk＜0,combining the above two estimates,we can easily get

Thus,it is easy to get

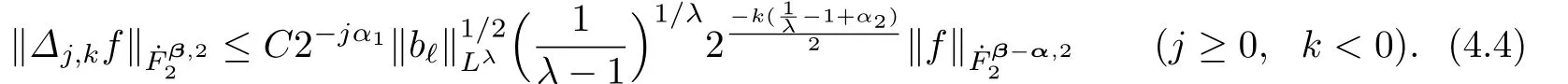
Similarly,ifj＜0 andk≥0,we may also obtain

4.2 The Casep=q

For the case,by using Lemma 3.4,we have

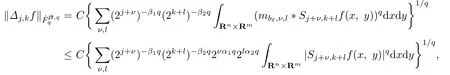
which implies

4.3 The Case

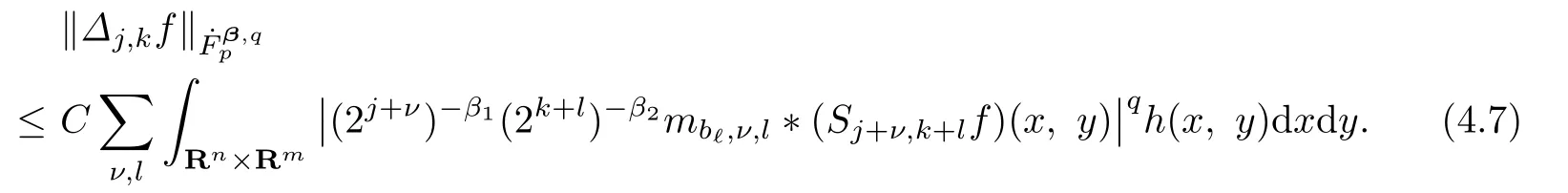
From Lemma 3.5,we get

Here the de finition of the operatoris de fined by

Using the method of rotation and the boundedness of Hardy-Littlewood maximal function on thespace,we obtain

Thus,we have

which implies

Using duality and takingq=2 in(4.9),we may obtain

For the casej≥0 andk≥0,we have the following estimates if we interpolate between (4.2)and(4.10).

Thus,ifj≥0 andk≥0,we have the following estimates if we interpolate between(4.9) and(4.11),

For the casej≥0 andk＜0,by interpolation(4.4)and(4.10),we have

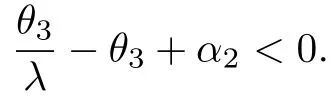
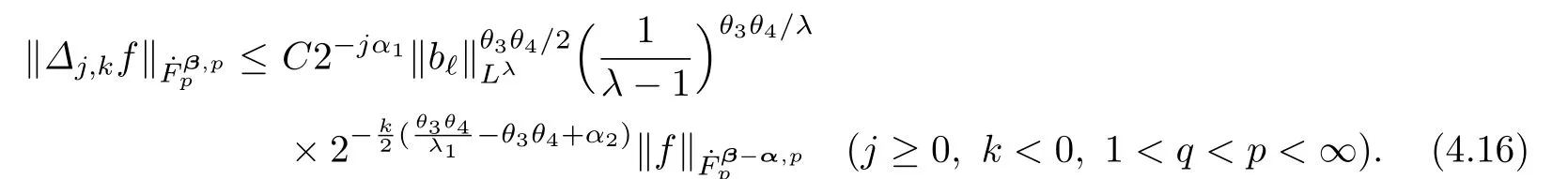
Now,we may denoteand0 such that

Similarly,for the caseandthere existsandsatisfying

4.4 Proof of Theorem 1.3

Now,we are ready to prove Theorem 1.3.Without loss of generality,we assume thatα1≥α2.

For the casej≥0 andk≥0,from(4.12),we have

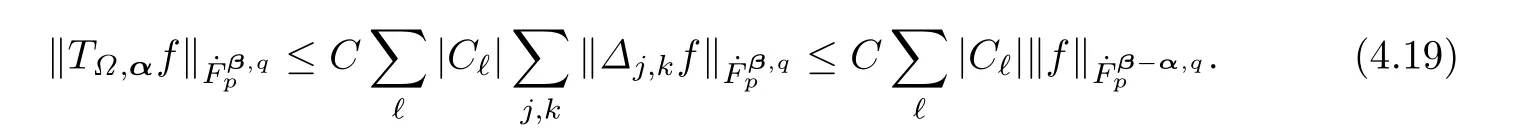
On the other hand,ifandusing(4.14),one has

Asα1≥α2,we have

and

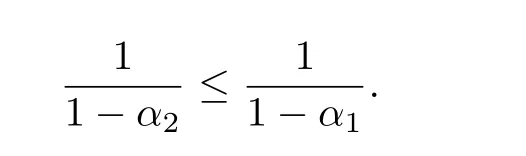
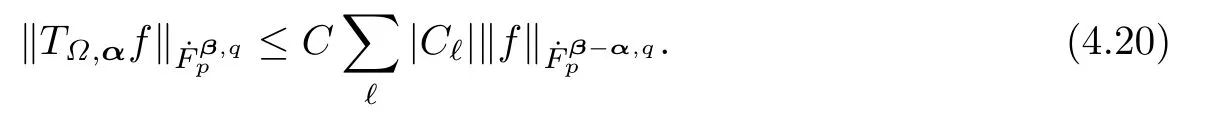
and

Thus,we can choose

Obviously,it is easy to see

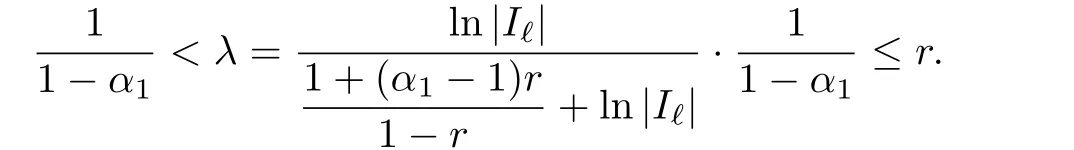
Then,by a simple computation and the factwe obtain

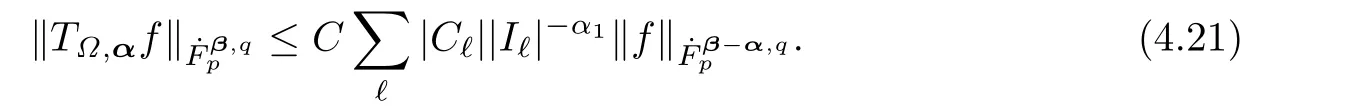
For the casej≥0 andk＜0,using(4.17),we have

By a similar argument as in the proof of(4.20)and(4.21),we may get

and

Similarly,for the casej＜0 andk≥0,we have

and

Combing(4.19)–(4.25),we have

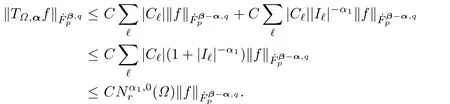
Consequently,Theorem 1.3 has been proved in the caseSinceβ1andβ2are arbitrary numbers,then by the duality theory,we conclude that Theorem 1.3 is true for alland the proof of Theorem 1.3 is completed.

[1]Duoandikoetxea J.Multiple singular integtrals and maximal functions along hypersurfaces.Ann.Inst.Fourier,1986,36:185–206.

[2]Fe ff erman R.Singular integrals on product domains.Bull.Amer.Math.Soc.,1981,4:195–201.

[3]Chen J C.Lpboundedness of singular integrals on product domains.Sci.China,Ser.A,2001,44:681–689.

[4]Chen J C,Wang H.Singular integral operators on product Triebel-Lizorkin spaces.Sci.China Math.,2010,53:335–346.

[5]Wang H,Chen J C.The maximal super-singular integral operators on product spaces.Sci. China Math.,2011,54:2615–2626.

[6]Jiang Y S,Lu S Z.A class of singular integral operators with rough kernels on product domain.Hokkaido Math.J.,1995,24:1–7.

[7]Duoandikoetxea J,Rubio de Francia J-L.Maximal and singular integral operators via Fourier transform estimates.Inv.Math.,1986,84:541–561.

[8]Fan D S,Guo K H,Pan Y B.Singular integrals with rough kernels on product spaces.Hokkaido Math.J.,1999,28:435–460.

[9]AL-Hasan A J,Fan D S.A singular integral operator related to block spaces.Hokkaido Math. J.,1999,28:285–299.

[10]Jiang Y S,Lu S Z.Lpboundedness for a class of maximal singular integrals.Acta Math.Sinica(Chin.Ser.),1992,35:63–72.

[11]Jiang Y S,Lu S Z.A note on a class of singular integral operators.Acta Math.Sinica(Chin. Ser.),1993,36:555–562.

[12]Yu X,Lu S Z.Boundedness for a class of fractional integrals with a rough kernel related to block spaces.Front.Math.China,2016,11:173–187.

[13]Taibleson M H,Weiss G.Certain function spaces associated with a.e.convergence of Fourier series.in:University of Chicago Conference,in honor of Zygmund:Woodsworth,1983:95–113.

[14]Lu S Z.On block decomposition of functions.Scientia Sinica,1984,27:585–596.

[15]Lu S Z.Taibleson M H,Weiss G.On the a.e.Convergence of Bochner-Riesz Means of Multiple Fourier Series.in:Harmonic Analysis,Lecture Notes in Mathematics,Berlin:Springer-Verlag, 1982:311-318.

[16]Lu S Z.Applications of some block spaces to singular integrals.Front.Math.China,2007,2: 61–72.

[17]Lu S Z,Taibleson M H,Weiss G.Spaces Generated by Blcks.Beijing:Beijing Normal University Press,1989.

[18]Triebel H.Theory of Function Spaces.Birkhauser,Basel:Springer Monographs in Mathematics,1983.

[19]Wang M.Boundedness of certain operators on product spaces(in Chinese).Ph.D.Thesis, Hangzhou:Zhejiang University,2002.

[20]Fan D S,Sato S.Singular and fractional integrals along variable surfaces.Hokkaido Math.J., 2006,35:61–85.

A

1674-5647(2017)03-0259-15

10.13447/j.1674-5647.2017.03.06

date:April 4,2016.

The NSF(11561057,11226104)of China,the NSF(20151BAB211002,20151BAB201007) of Jiangxi Province,the Science Foundation(GJJ151054,GJJ151061)of Jiangxi Education Department,and the Scienti fic Research Project of Shangrao Normal University.

*

.

E-mail address:zhanghuihuinb@163.com(Zhang H H),yx2000s@163.com(Yu X).

42B20,42B25