On ∂-reducible 3-manifolds Which Admit Complete Surface Systems

Zhao YanLei Feng-chunand Li Feng-ling

(1.School of Mathematical Sciences,Dalian University of Technology,Dalian,116024)

(2.College of Mathematics and Physics,Bohai University,Jinzhou,Liaoning,121013)

On ∂-reducible 3-manifolds Which Admit Complete Surface Systems

Zhao Yan1,2,Lei Feng-chun1and Li Feng-ling1

(1.School of Mathematical Sciences,Dalian University of Technology,Dalian,116024)

(2.College of Mathematics and Physics,Bohai University,Jinzhou,Liaoning,121013)

In the present paper,we consider a class of compact orientable 3-manifolds with one boundary component,and suppose that the manifolds are∂-reducible and admit complete surface systems.One of our main results says that for a compact orientable,irreducible and∂-reducible 3-manifoldMwith one boundary componentFof genusn＞0 which admits a complete surface systemS′,ifDis a collection of pairwise disjoint compression disks for∂M,then there exists a complete surface systemSforM,which is equivalent toS′,such thatDis disjoint fromS.We also obtain some properties of such 3-manifolds which can be embedded inS3.

complete surface system,∂-reducibility,Heegaard splitting

1 Introduction

LetJ={J1,···,Jn}be a collection of pairwise disjoint simple closed curves on a connected orientable closed surfaceSof genusn.If the surface obtained by cuttingSopen alongJis a 2n-punctured 2-sphere,we callJa complete curve system(or simply,CCS).Two CCSs onSare equivalent if one can be obtained from another via finite number of band moves (de fined in Section 2)and isotopies.

LetMbe a compact orientable 3-manifold with one boundary componentF,andS={S1,···,Sn}a collection ofnpairwise disjoint connected orientable surfaces properly embedded inM.Ifis a CCS onF,we callSa complete surface system (or simply,CSS)forM.Two CSSsS1andS2forMare equivalent if∂S1and∂S2are equivalent onF.

It is well known that any two complete disk systems in a handlebody are equivalent,thatis,the equivalent classes of complete disk systems for a handlebody are unique.Clearly,a complete system of disks for a handlebodyHnof genusnis a CSS forHn.By Corollary 1.4 in[1],the complete disk systems are the only CSSs in a handlebodyHn.

In this paper,we consider a class of compact orientable 3-manifolds with one boundary component,and suppose that the manifolds are∂-reducible and admit CSSs.One of our main results says that for a compact orientable,irreducible and∂-reducible 3-manifoldMwith one boundary componentFof genusn＞0 which admits a CSSS′,ifDis a collection of pairwise disjoint compression disks for∂M,then there exists a CSSSforM,which is equivalent toS′,such thatDis disjoint fromS.We also obtain some properties of such 3-manifolds which can be embedded inS3.

The paper is organized as follows.Section 2 contains some necessary preliminaries.In Section 3,we prove one of the main results mentioned as above,and in Section 4,we obtain some properties of such 3-manifolds which are 3-submanifolds ofS3.

2 Preliminaries

The terminology and de finitions used in the paper are all standard,see for example,refer to[2]–[3].

2.1 Complete Surface Systems for 3-manifolds

In this part,we introduce some de finitions on complete surface systems for 3-manifolds.

De finition 2.1Let S=Snbe a closed orientable surface of genus n.A collection of n pairwise disjoint simple closed curves J on S is called a complete curve system(or simply, CCS)for S if the surface obtained by cutting S open along J is a2n-punctured sphere.

De finition 2.2Let S=Snbe a closed orientable surface of genus n,n≥2.

(1)Let J1,J2be two disjoint essential simple closed curves on S.Let γ be a simple arc on S with one endpoint lying in J1,and another endpoint lying in J2,and the interior of γ is disjoint from J1and J2∪∪be a compact regular neighborhood ofon S.Denote the component of∂N,which is parallel to neither J1nor J21and J2along γ.

(2)let γ be a simple arc on S with one endpoint lying in Ji,and another endpoint lying in Jj,and the interior of γ isdisjoint fromLet Jijbe the band sum of Jiand Jjalong γ.By isotopy,we mayassume that Jijis disjoint from the curves in J.It is easy to see that J′is still a CCS for S.We call J′an elementary band move of J along γ.

(3)Two CCSs C1and C2on S are called equivalent if one can be obtained from another by a finite number of elementary band moves and isotopies.

It is clear that ifJ′is a band move ofJ,thenJis also a band move ofJ′.

De finition 2.3Let M be a compact3-manifold and S a boundary component of M with g(S)=n≥1=1,2,···,n.If{J1,···,Jn}is a CCS for S,we call S a complete surface system(or simply,CSS)for M with respect to S.We call two CSSs S1and S2for M with respect to S are equivalent if the corresponding CCSs∂S1and∂S2are equivalent on S.

By Corollary 1.4 in[1],a complete disk system in a handlebodyHnis the only CSS. In particular,for a complete disk systeminHn,ifJis a CCS on∂Hnwhich is equivalent to∂D,thenJbounds a complete disk system forH.

By a similar argument to that of complete disk systems in a handlebody,one can get the following proposition.

Proposition 2.1Let M be a compact3-manifold,and S a boundary component of M with genus n＞0.Let S be a CSS for M with respect to S.Then any CCS J′on S which is equivalent to∂S also bounds a CSS for M.

De finition 2.4Let M be a compact orintable3-manifold,and F a compact surface properly embedded in M.We say that F is compressible in M if

(1)either F is a2-sphere which bounds a3-ball in M;or

(2)F is a disk either contained in∂M or properly embedded in M and F cuts out a3-ball from M;or

(3)there exists a disksuch thatand∂D is an essential loop in F.In the case,we call D a compression disk for F.

We say that F is incompressible in M if F is not compressible in M.If∂M is compressible in M,we say that M is∂-reducible.Otherwise,we say that M is∂-irreducible.

De finition 2.5Let M be a compact orientable3-manifold.If M contains an incompressible2-sphere,we say that M is reducible.Otherwise,M is irreducible.

De finition 2.6Let Mibe a compact orientable3-manifold with one boundary Fi,anda disk,i=1,2.Let h:called the boundary connected sum of M1and M2,and is denoted byorwhereis a compression disk of∂M in M which cuts M into M1and M2

It is obvious that the operationon 3-manifolds is associative and commutative. We say that a decompositionis nontrivial if none of the factorsM1,···,Mpis a 3-ball.

Similar to the uniqueness theorem of the prime decompositions of connected sums for compact orientable 3-manifolds,the following theorem is well known in[3].

Theorem 2.1Let M be an orientable irreducible3-manifold with one boundary component of genus≥1.Then M has a non-trivial boundary connected sum decomposition as

such that at most one of M1,···,Mk,say M1,is a handlebody of genus≥1,and each Mi, if any,is∂-irreducible,

Moreover,the decompositions in(2.1)are unique up to homeomorphism and re-ordering.

The decomposition in(2.1)is called a standard boundary connected sum decomposition forM,and ifMis∂-reducible,the collection{Δ1,···,Δk−1}of pairwise disjoint disks properly embedded inMis called a standard disk set for the standard decomposition.

2.2 Heegaard Splittings

In this part,we review some fundamental facts on Heegaard splittings of 3-manifolds.

De finition 2.7Let F be a closed orientable connected surface,and let I=[0,1]be the unit interval.A compression body W is a3-manifold obtained by attaching22-spheres by3-balls.Denote the boundary componentin∂W byandis a handlebody of genusIn W,J can be naturally extended to a collection E of pairwise disjoint essential disks properly embedded in W.We call E a de fining disk set for W.

De finition 2.8Let M be a compact connected orientable3-manifold.If there exists a connected orientable surface F in M such that F cuts M into two compression bodies V1and V2called a Heegaard splitting of M,and g(F)is also called the genus of the splitting.

It is a well known fact that a compact connected orientable 3-manifold always admits a Heegaard splitting.

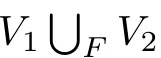
In the following we brie fl y collect some well-known facts that are used in Sections 3 and 4.

Theorem 2.2[4]Any Heegaard splitting of genusfor S3is stabilized.

Theorem 2.3[5]Any Heegaard splitting of a∂-reducible3-manifold is∂-reducible.

Proposition 2.2[6]Let A be a spanning essential annulus in a compression body.Then there exists a de fining disk set E for W such that A is disjoint from E.

Theorem 2.4[7]Let X be a compact connected3-submanifold of S3.Then X can be re-embedded in S3so that the complement of the image of X is a union of handlebodies.

3 ∂-reducible 3-manifolds Which Admit CSSs

We first show the following theorem.

Theorem 3.1Let M be a compact orientable,irreducible and∂-reducible3-manifold with one boundary component F of genus n＞0.Suppose that M admits a CSS S.Let D=for M which is equivalent to S,such that

Proof.Choose a CSSforMsuch thatS′is equivalent toS,S′andDare in general position,and the number of components of the intersection ofandis minimal over all CSSs inMwhich are equivalent toS.We may assume thatS′is incompressible inM.We show that the minimality implies that

If it is not the case,then

Sinceincompressible inM,cbounds a disk.Setand pusho ff△slightly by isotopy.The CSSobtained fromby replacingbyhas clearly less intersection number withthan that ofandThis contradicts to the choice ofS′.

Setandis a simple arc onFsuch that

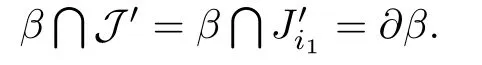
At least one ofandsay,,is non-trivial onF.Set

Next we show thatis equivalent toonF.

In fact,letPbe the 2n-punctured sphere obtained by cuttingFopen alongDenote byandthe two cutting sections ofin∂P.is a simple closed curve onP,soseparatesPinto two planar surfacesP1andis a simple arc onPwith∂βlying in one ofandsinceThus each of∂P1andcontains one ofandsay,is a component ofandis a component of

Assume thatwhere foris one of the two cutting sections of someandSinceP1is a connected planar surface,there exists a collectionof pairwise disjoint properly embedded simple arcs onP1such thatconnectsandMake the band sumsonP1.It is clear that the resulting simple closed curve is parallel toKi1.Thus,

can be obtained frombyqelementary band moves,sois equivalent toonF.

By Proposition 2.1,bounds a collectionofnpairwise disjoint orientable surfaces inM,and each has one boundary component.By Claim 1,we may further assume that the intersection of the union of surfaces inand the union of disks inDhas no circle components.Note that

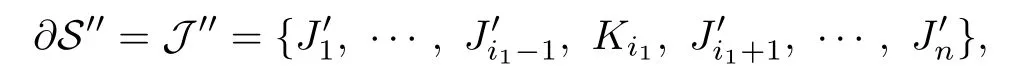
so we have

again contradicting to our choice of

As direct consequences of Theorem 3.1,we have the following corollary.

4 ∂-reducible 3-submanifolds in S3

In the following,we consider a∂-reducible 3-submanifoldMofS3,which has one boundary component.

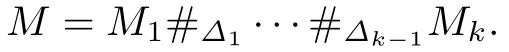
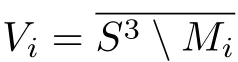
Corollary 4.1Let M be a3-submanifold of S3with one boundary component F of genuswhich is compressible in M.Suppose that M has a standard boundary connected sumdecompositionThen M can be re-embedded into S3,such thatthe complementis a handlebody,and for eachbounds a diskin V.Moreover,each Miis an exterior of a nontrivial knot inand M admits a CSS.

Since eachcan be re-embedded intosuch that the complement ofinS3is a solid torus,andis incompressible insois an exterior of a nontrivial knotnfor eachLebe a Seifert surface inMiforThenis a CSS forM.

Corollary 4.2Let M be a3-submanifold of S3with one boundary component F of genuswhich is compressible in M.Suppose that M has a standard boundary connected sum decomposition.Then M1is an exterior of a nontrivial knot in S3,and M admits a CSSwhere S is a Seifert surface in M1.

Proof.It follows directly from Theorem 4.2 and Corollary 4.1.

[1]Lei F C.Complete systems of surfaces in 3-manifolds.Math.Proc.Cambridge Philos.Soc.,1997,122(1):185–191.

[2]Hempel J.3-manifolds.New Jersey:Princeton University Press,1976:14–65.

[3]Jaco W.Lectures on Three Manifold Topology.Providence,R.I.:American Mathematical Society,1980:18–50.

[4]Waldhausen F.Heegaard-Zerlegungen der 3-sph¨are.Topology,1968,7(2):195–203.

[5]Casson A,McA Gordon C.Reducing Heegaard splittings.Topology Appl.,1987,27(3):275–283.

[6]Schultens J.The classi fication of Heegaard splittings for(compact orientable surfaces)×S1.Proc. London Math.Soc.,1993,67(2):425–448.

[7]Fox R H.On the imbeddings of polyhedra in 3-space.Ann.of Math.(2),1948,49(2):462–470.

tion:57M25,55Q20

A

1674-5647(2017)03-0215-08

10.13447/j.1674-5647.2017.03.03

date:Feb.4,2016.

The NSF(11329101,11431009,11329101,11471151 and 11401069)of China and the Fundamental Research Funds(DUT16LK40)for the Central Universities.

E-mail address:zhaoyan jinzh@126.com(Zhao Y).