C2Continuous Quartic Hermite Spline Curves with Shape Parameters

Li Jun-cheng and Liu Cheng-zhi

(College of Mathematics and Finance,Hunan University of Humanities,Science and Technology, Loudi,Hunan,417000)

C2Continuous Quartic Hermite Spline Curves with Shape Parameters

Li Jun-cheng and Liu Cheng-zhi

(College of Mathematics and Finance,Hunan University of Humanities,Science and Technology, Loudi,Hunan,417000)

Communicated by Ma Fu-ming

In order to relieve the de ficiency of the usual cubic Hermite spline curves, the quartic Hermite spline curves with shape parameters is further studied in this work.The interpolation error and estimator of the quartic Hermite spline curves are given.And the characteristics of the quartic Hermite spline curves are discussed. The quartic Hermite spline curves not only have the same interpolation and continuity properties of the usual cubic Hermite spline curves,but also can achieve local or global shape adjustment andC2continuity by the shape parameters when the interpolation conditions are fixed.

Hermite spline curve,interpolation curve,shape adjustment,C2continuous

1 Introduction

With the development of geometric design industry,the shapes of curves often need to be changed freely.Hence,the curves with shape parameters have been paid more and more attention by many researchers in geometric modeling.Such as the B´ezier curves with shape parameters(see[1]–[3]),the B-spline curves with shape parameters(see[4]–[6]),the trigonometric spline curves with shape parameters(see[7]–[9]),and so on.Those curves with shape parameters not only inherit the similar or same properties of the corresponding usual curves,but also have better performance ability because of the shape parameters.

As a class of interpolation curves,the cubic Hermite spline curves have been widelyused in many fields.However,when the interpolation conditions are fixed,the usual cubic Hermite spline curves can only beC1continuous and theirs shape cannot be changed. Hence,the de ficiency of the usual cubic Hermite spline curves limits their applications in practical engineering.For relieving the de ficiency of the usual cubic Hermite spline curves, construction of the Hermite spline curves with shape parameters would be an e ff ective way. Liet al.[10]presented a class of quartic Hermite spline curves with parameters,which could achieve shape adjustment andC2continuity by the parameters.When using the Hermite spline presented by Liet al.[10]to constructC2curves,the initial value of the parameter should be set in advance and the other parameters are calculated by the recursion formula. Although this method is simple and convenient,its disadvantages lie in that the initial value of the parameter need to be given arti ficially.When the initial value of the parameter is not appropriate,the curves would be not ideal.In addition,Liet al.[10]did not give the interpolation error and its estimator of the quartic Hermite spline curves.For these reasons, the main purpose of this work is to further discuss the quartic Hermite spline curves with shape parameters presented by Liet al.[10].The relationship between the initial parameter and the other parameters is derived,and then the minimum approximation error is used to determine the value of initial parameter,so that selection of the parameters has stronger maneuverability.Besides,the interpolation error and estimator of the quartic Hermite spline curves are given.

The rest of this paper is organized as follows.In Section 2,the usual cubic Hermite spline curves are discussed.In Section 3,the quartic Hermite basis functions with shape parameters are de fined,and the properties of the basis functions are given.In Section 4, de finition and properties of the quartic Hermite spline curves with shape parameters are given.In Section 5,characteristics of the quartic Hermite spline curves are studied.A short conclusion is given in Section 6.

2 The Usual Cubic Hermite Spline Curves

Hermite spline curves can be expressed as follows(see[11]):

whereandare the usual cubic Hermite basis functions de fined as follows:

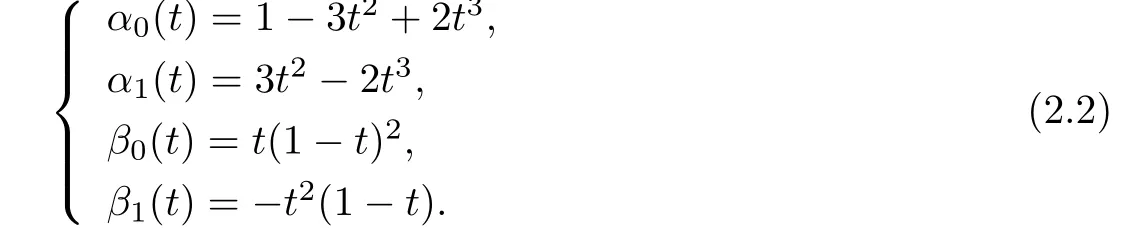
By a simple deduction,the usual cubic Hermite basis functions expressed as(2.2)satisfythat

and

It is known that the usual cubic Hermite spline curves expressed as(2.1)have the properties as follows:

(a)Interpolation:The usual cubic Hermite spline curves interpolate all the data points

(b)Continuity:The usual cubic Hermite spline curves areC1continuous,viz.,

Because of the interpolation and continuity,the usual cubic Hermite spline curves have been widely used in di ff erent areas.However,the usual cubic Hermite spline curves have the following de ficiency whenare fixed.

(a)The shape of the usual cubic Hermite spline curves cannot be changed.

(b)The usual cubic Hermite spline curves can only beC1continuous.

In order to relieve the de ficiency of the usual cubic Hermite spline curves,the quartic Hermite spline curves with shape parameters will be proposed in the following work.

3 The Quartic Hermite Basis Functions

Firstly,the de finition of the quartic Hermite basis functions of[10]is given as follows.

De finition 3.1Thefollowingfour functions oft are called quartic Hermite basis functions:

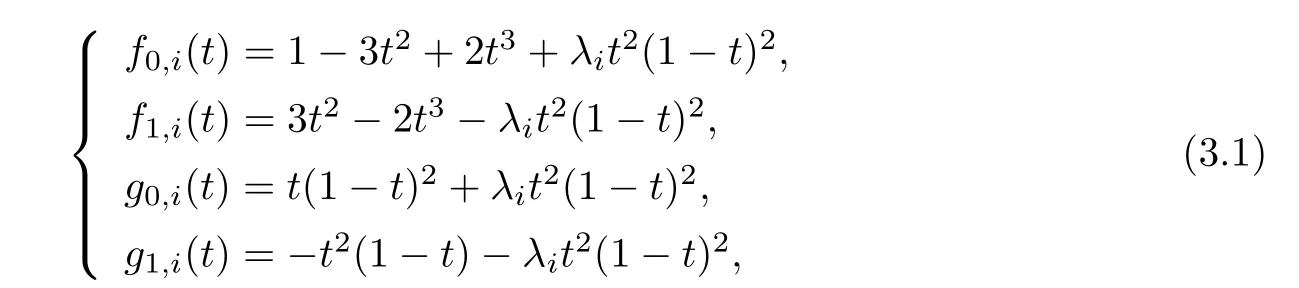
Remark 3.1From(2.2)and(3.1),the quartic basis Hermite functions would degenerate into the usual cubic Hermite basis functions whenλi=0.

Theorem 3.1The quartic Hermite basis functions de fined as(3.1)have the properties as follows:

(a)On the endpoints,the quartic Hermite basis functions satisfy that

(b)For any t∈[0,1],one has

(c)1,i(t)and g1,i(t)are monotone decreasing about λi.

Proof.(a)(3.1)can be rewritten as follows:

By(3.4),we have

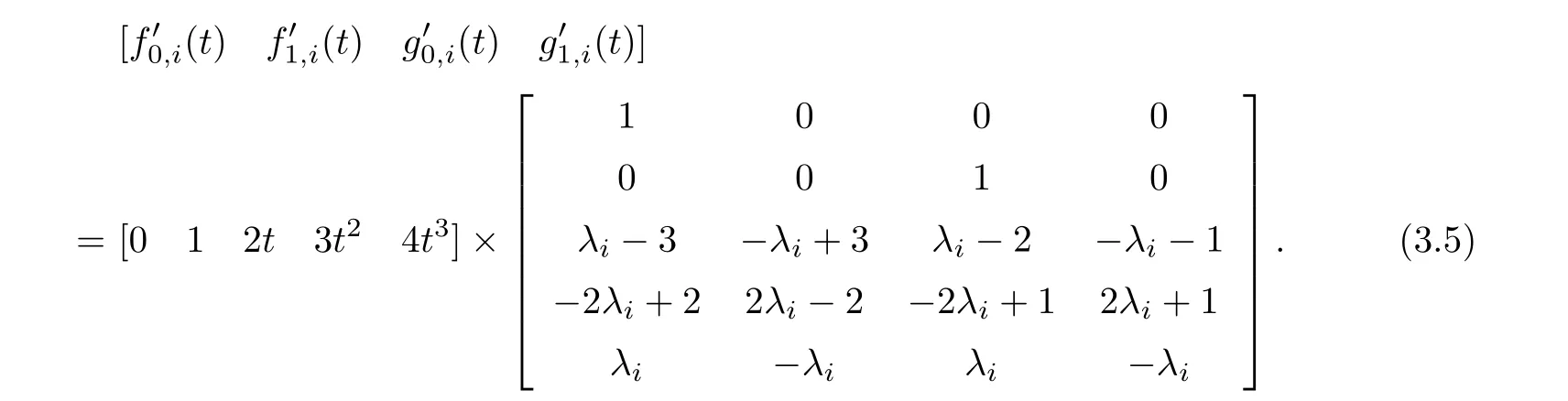
Then(3.2)can be easily obtained by puttingt=0 andt=1 into(3.4)and(3.5).

(b)By a simple deduction,(3.3)follows obviously.

(c)For a fixed,we have

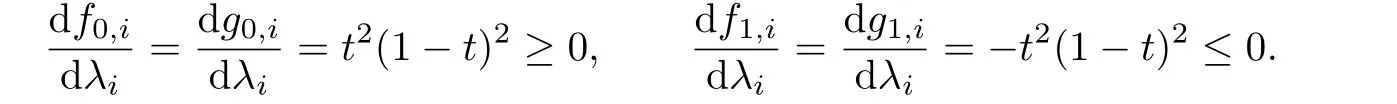
Then,f0,i(t)andg0,i(t)are monotone increasing aboutλiwhilef1,i(t)andg1,i(t)are monotone decreasing aboutλi.

Remark 3.2Theorem 3.1 shows that the quartic Hermite basis functions have the same properties of the usual cubic Hermite basis functions.Shapes of curves of the usual cubic Hermite basis functions cannot be changed while various shapes of curves of the quartic Hermite basis functions can be gotten by setting di ff erent values of the shape parameterλi.

Fig.3.1 shows curves of the quartic Hermite basis functions for di ff erent values ofλi, whereλiis set forandrespectively.

Fig.3.1 Curves of the proposed basis functions for di ff erent shape parameters

4 The Quartic Hermite Spline Curves with Shape Parameters

On base of the quartic Hermite basis functions,the quartic Hermite spline curves of[10]can be de fined as follows.

De finition 4.1[a,b]the corresponding quartic Hermite spline curves can be de fined as follows:

(3.1).

Remark 4.1The quartic Hermite spline curves de fined as(4.1)are composed bynsegments of curves.

Remark 4.2From Remark 3.1,the quartic Hermite spline curves de fined as(4.1)would degenerate into the usual cubic Hermite spline curves when

The quartic Hermite spline curves de fined as(4.1)have the properties as follows.

Theorem 4.1Given(i=0,1,2,···,n),the quartic Hermite spline curves de fined as(4.1)interpolate all the data points(xi,yi)(i=0,1,2,···,n)and can be C1continuous.

Proof.By(3.1)and(4.1),we have

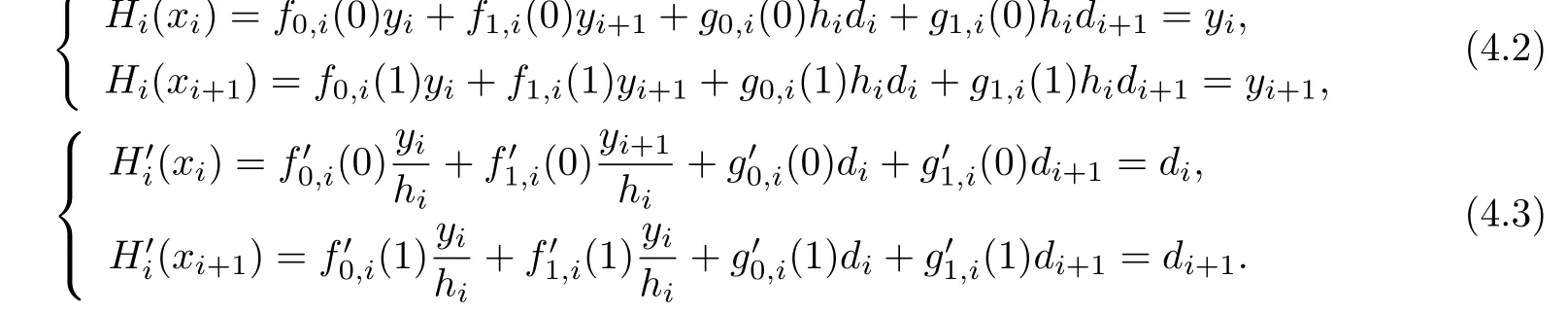
(4.2)shows that the quartic Hermite spline curves interpolate all the data points(xi,yi) (i=0,1,2,···,n).

From(4.2)and(4.3),we have

(4.4)shows that the quartic Hermite spline curves areC1continuous.

Remark 4.3Theorem 4.1 shows that the quartic Hermite spline curves have the same interpolation and continuity properties of the usual cubic Hermite spline curves.

Given a functionthe corresponding quartic Hermite spline curves have the interpolation remainder as follows.

Theorem 4.2Suppose that the given functionhas4-order derivative,is a division of

and the error estimate is

Proof.From Theorem 4.1 we have

(4.7)shows that the interpolation remainder of the corresponding quartic Hermite spline curves de fined in[xi,xi+1]can be set as follows:

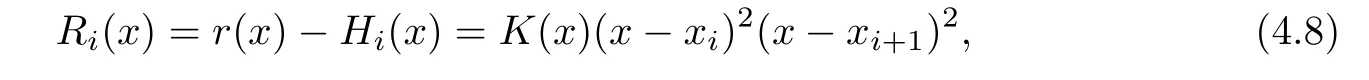
whereK(x)is an undetermined function.

Suppose

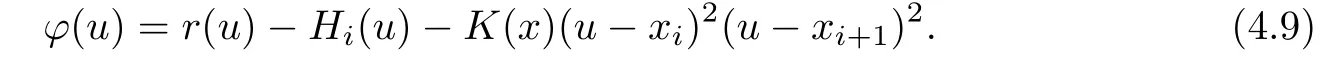
By a simple deduction,we can get

(4.10)shows thatφ(u)has five zero pointsx,xi(twofold)and(twofold).Then,has four zero points,has three zero points,has two zero points,andhas one zero pointBy(4.9),we have

From(4.1),we have

By(4.11)and(4.12),we have

Taking(4.13)into(4.8),we get

From(4.5),one has

SetIt is not difficult to obtain that

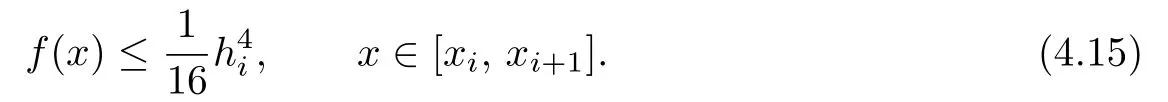
From(4.14)and(4.15),we have

Remark 4.4From(4.6),one haswhenwhich shows that the quartic Hermite spline curves are convergent.

5 Characteristics of the Quartic Hermite Spline Curves

5.1 Shape Adjustability

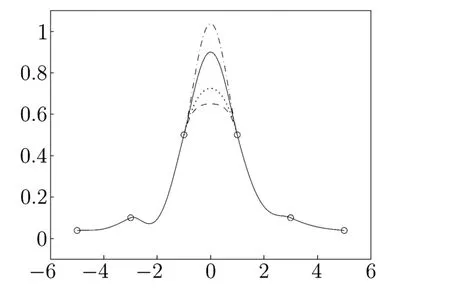
Fig.5.1 Local adjustment of the quartic Hermite spline curves

Example 5.2Given a function,letThen the corresponding quartic Hermite spline curves are composed by three segments of curves.Fig.5.2 shows the global adjustment of the quartic Hermite spline curves by settingwhere the dashed lines,dotted lines, solid lines and dash-dotted lines are set forandrespectively.

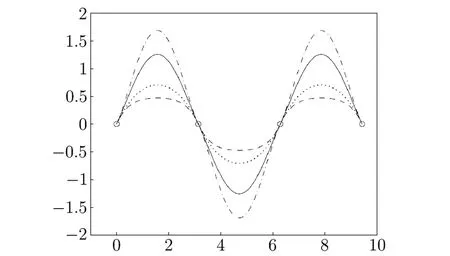
Fig.5.2 Global adjustment of the quartic Hermite spline curves

5.2C2Continuity

It is known that,the usual cubic Hermite spline curves can only beC1continuous whenare fixed,while the quartic Hermite spline curves can beC2continuous by the shape parametersas follows.

Theorem 5.1Given(i=0,1,2,···,n),the quartic Hermite spline curves de fined as(4.1)can be C2continuous when the shape parameters λi(i=0,1,2,···,n−1)meet the conditions as follows:

where

Proof.In order to make the quartic Hermite spline curves beC2continuous,then for

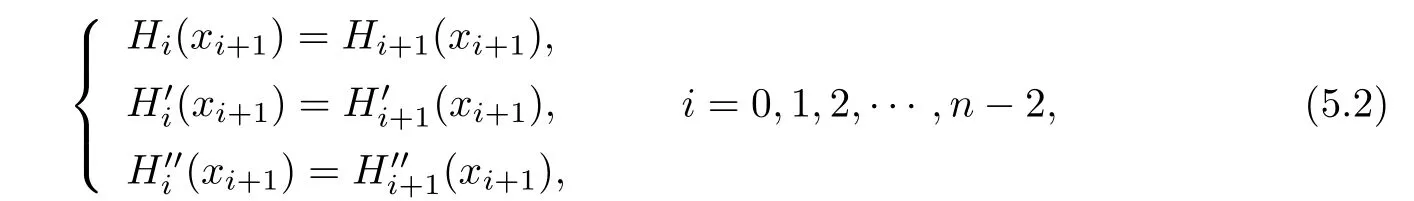
from(4.4),only

in(5.2)are needed to be satis fied.

By(4.1),we have

From(3.5),we have

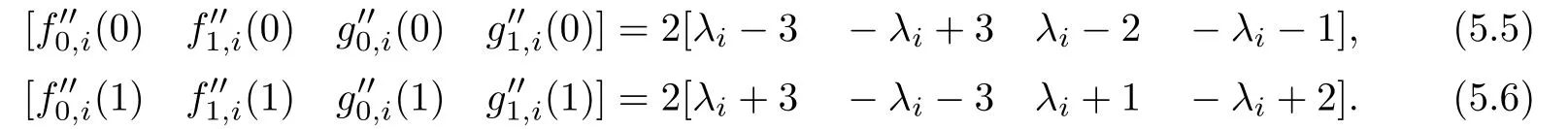
By taking(5.5)and(5.6)into(5.4),we have

Then,it is not difficult to get(5.1)by substituting(5.7)into(5.3).

Remark 5.1Theorem 5.1 shows that the shape parameterscan be got from(5.1)after the first shape parameterλ0is determined,and then theC2continuous quartic Hermite spline curves can be naturally obtained.

Example 5.3Given a functionletIf the first shape parameterλ0is speci fied asthen the shape parameterscan be got from(5.1)as follows:

The correspondingC2continuous quartic Hermite spline curves for specifying di ff erent values of the first shape parameterλ0are shown in Fig.5.3,where the solid lines and dotted lines are the quartic Hermite spline curves for specifyingandrespectively.

Fig.5.3 Di ff erent shapes of theC2continuous quartic Hermite spline curves

Remark 5.2It is not difficult to know that the shape of the correspondingC2continuous quartic Hermite spline curves is complete determined by the first shape parameterλ0whenare fixed.Hence,how to determine a proper value of the first shape parameterλ0is the key when constructing theC2continuous quartic Hermite spline curves.

A method for determining the value of the first shape parameterλ0is presented as follows.

By(5.1),we have

where

Let

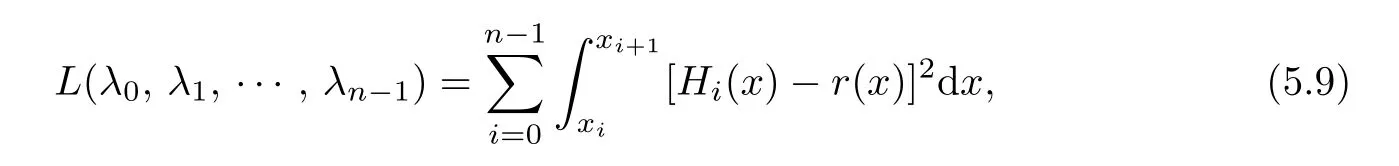
whereis a given function,is the corresponding quartic Hermite spline curve de fined in the interval

Taking(5.8)into(5.9),then(5.9)can be simpli fied as follows:

In order to obtain the minimum interpolation error,then

It is clear thatL(λ0)expressed as(5.10)is a quadratic function aboutλ0.Therefore,(5.11) has only one solution,and the solution is the optimum parameter ofAfter the optimum shape parameter ofis determined,the other shape parametersof(i=1,2,3,···,n−1)can be got from(5.8).Then,the correspondingC2continuous quartic Hermite spline curves are naturally obtained from(4.1).

Example 5.4Given a function,the selectedand the calculated shape parametersλiof the correspondingC2continuous quartic Hermite spline curvesHi(x)are shown in Table 5.1,where the first shape parameterλ0is got from(5.10) and(5.11),the other shape parametersλiare obtained from(5.8).

Table 5.1The given interpolation conditions and calculated shape parameters

Fig.5.4 shows the curve ofr(x)and the correspondingC2continuous quartic Hermite spline curvesHi(x),where the dotted lines and solid lines are the function curve and spline curve,respectively.

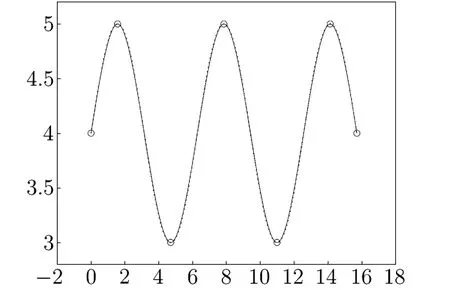
Fig.5.4 The function curve and theC2continuous quartic Hermite spline curves

6 Conclusion

The quartic Hermite spline curves with shape parameters have the same structure as the usual cubic Hermite spline curves.While keeping the same properties of the cubic Hermitespline curves,the quartic Hermite spline curves can be local or global adjusted andC2continuous by the shape parameters when the interpolation conditions are fixed.The examples illustrate the feasibility of this method.Furthermore,the quartic Hermite spline surfaces with shape parameters could be constructed by using tensor product.The surfaces would enjoy the same characteristics with the curves.

[1]Yang L Q,Zeng X M.B´ezier curves and surfaces with shape parameters.Int.J.Comput. Math.,2009,86:1253–1263.

[2]Yan L L,Liang Q F.An extension of the B´ezier model.Appl.Math.Comput.,2011,218: 2863–2879.

[3]Bashir U,Abbsa M,Ali J M.TheG2andC2rational quadratic trigonometric B´ezier curve with two shape parameters with applications.Appl.Math.Comput.,2013,219:10183–10197.

[4]Liu X M,Xu W X,Guan Y,Shang Y Y.Hyperbolic polynomial uniform B-spline curves and surfaces with shape parameter.Graphical Models,2010,72:1–6.

[5]Juh´asz I,Ho ff mann M.On the quartic curve of Han.J.Comput.Appl.Math.,2009,223: 124–132.

[6]Yan L L,Liang J F.A class of algebraic-trigonometric blended splines.J.Comput.Appl. Math.,2011,235:1713–1729.

[7]Wang G Z,Fang M E.Uni fied and extended form of three types of splines.J.Comput.Appl. Math.,2008,216:498–508.

[8]Juh´asz I,R´oth´A.Closed rational trigonometric curves and surfaces.J.Comput.Appl.Math., 2010,234:2390–2404.

[9]Han X L,Zhu Y P.Curve construction based on five trigonometric blending functions.BIT Numer.Math.,2012,52:953–979.

[10]Li J C,Liu C Y,Yang L.The quartic Hermite interpolating splines with parameters(in Chinese).J.Comput.Appl.,2012,32:1868–1870.

[11]Farin,G.Curves and Surfaces for Computer-Aided Geometric Design(4th ed).Maryland: Elsevier Science&Technology Books,1997.

tion:65D07,65D05

A

1674-5647(2017)03-0193-12

10.13447/j.1674-5647.2017.03.01

date:Dec.31,2015.

Hunan Provincial Natural Science Foundation(2017JJ3124)of China,and the Scienti fic Research Fund(14B099)of Hunan Provincial Education Department of China.

E-mail address:lijuncheng82@126.com(Li J C).