The New Structure Theorem of Right-e Wlpp Semigroups

Wang Chun-ru,Ren Xue-mingand Ma Si-yao

(1.Huaqing College,Xi’an University of Architecture and Technology,Xi’an,710043)

(2.Department of Mathematics,Xi’an University of Architecture and Technology, Xi’an,710055)

The New Structure Theorem of Right-e Wlpp Semigroups

Wang Chun-ru1,Ren Xue-ming2and Ma Si-yao2

(1.Huaqing College,Xi’an University of Architecture and Technology,Xi’an,710043)

(2.Department of Mathematics,Xi’an University of Architecture and Technology, Xi’an,710055)

Communicated by Du Xian-kun

Wlpp semigroups are generalizations of lpp semigroups and regular semigroups.In this paper,we consider some kinds of wlpp semigroups,namely right-ewlpp semigroups.It is proved that such a semigroupS,if and only ifSis the strong semilattice ofL-right cancellative planks;also if and only ifSis a spined product of a right-ewlpp semigroup and a left normal band.

wlpp semigroup,right-ewlpp semigroup,spined product

1 Introduction

According to Tang[1],a new generalized Green relationR∗∗on a semigroupSis de fined as follows:for anya,b∈S,

whereLis the usual Green relation.It is easy to verify thatR∗∗is a left congruence on any semigroup andA semigroupSis said to a wlpp semigroup if each classR∗∗ofScontains an idempotent ofSandfor anya∈Sandwhereis theR∗∗-class ofScontaining the elementa.It is easy to check that a regular semigroupSis a wlpp semigroup and a wlpp semigroup is a generalization of a regular semigroup.In this paper,we consider the following semigroups:

De finition 1.1[2]A wlpp semigroup S is called a right-e wlpp semigroup if xey=xye holds for anyand any x,with

We first have the following result for right-ewlpp semigroups which will be frequently used in the sequel.

Lemma 1.1If S is a right-e wlpp semigroup,then every R∗∗-class of S contains a unique idempotent.

Proof.Suppose thatSis a right-ewlpp semigroup anda∈S.Then there exists an idempotentsuch thata=ea.Hence,

Now ifthen

We denote the unique idempotent inofSbySinceSis a right-ewlpp semigroup, it follows that

Lemma 1.2If S is a right-e wlpp semigroup,then R∗∗is a congruence on S.

Proof.It is easy to see that the relationis an equivalence.To show thatR∗∗is compatible,letforThenby Lemma 1.1.Suppose thatfor anyx,y∈S1and anyc∈S.Since(c,c+)∈R∗∗,it follows thatButand henceL.Froma+=b+andwe haveandAgain,fromwe have

Suppose that(xca,yca)∈L.Sincewe obtain that(xcb,ycb)∈Land soR∗∗is a left congruence onS.Thus,we have proved thatR∗∗is a congruence onS.

Lemma 1.3Suppose that S is a right-e wlpp semigroup.Thenfor all a,b∈S.

Proof.LetSbe a right-ewlpp semigroup.we haveandThen,by Lemma 1.2,for allsinceR∗∗is a congruence onS. Thusby Lemma 1.1.

LetSbe a right-ewlpp semigroup.For alla,b∈S,we de fine a relationρbyaρbif and only ifa=fbfor some,whereis a rectangular band containing idempotentb+.

Lemma 1.4Let S be a right-e wlpp semigroup and ρ be the above relation de fined on S. Then ρ is a congruence on S.

Proof.We now claim thatρis an equivalent relation.Clearly,ρis re fl exive and symmetric. To show thatρis transitive,we first prove that ifaρb,thenE(a+)=E(b+)for anya,b∈S.

To prove our claim,letaρb.Thena=fbfor someby de finition ofρ.It is clear thatfa=a.By Lemma 1.3,we have

This implies thatwhich gives

Sincea=fbfor someandis a left zero band,it follows that

and so

by Lemma 1.3,which implies

Thus,

holds.

Now we prove thatρis transitive.Letaρbandbρc.Then we have

By the de finition ofandfor someIt follows that

sinceE(b+)is a left zero band.Consequently,aρcand henceρis an equivalent relation onS.

Finally,we prove thatρis compatible with the semigroup multiplication.

We first show thatρis right compatible.Suppose thataρbfora,b∈S.Thena=fbfor someClearly,

Sincefor anywe have

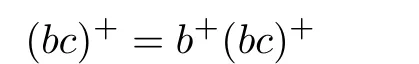
by Lemma 1.3.This shows

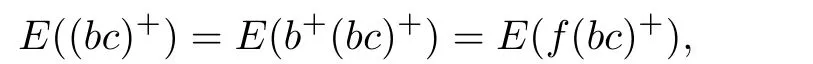
and soHence,acρbc.

It is clear thatρis also left compatible with semigroup multiplication,since every idempotent ofSis right central.Thus,ρis a congruence onS.

Lemma 1.5Let S be a right-e wlpp semigroup.If ab for a,b∈S,then aρbρ.

Proof.We first show that ifaR∗∗b,thenimplies thatfor anyand

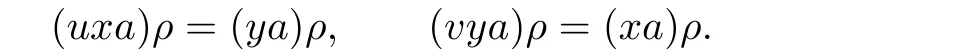
Then,by the de finition ofρ,we have

and

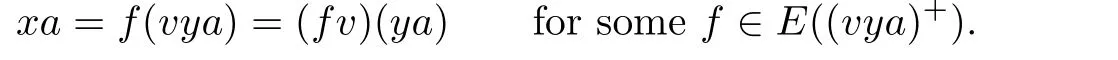
Lemma 1.6If S is a right-e wlpp semigroup,then

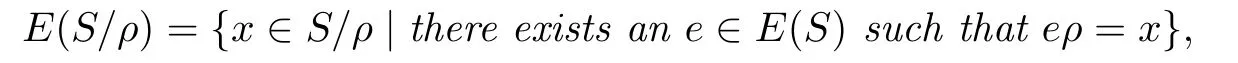
where ρ is the congruence considered in Lemma1.4on S.

Proof.Let

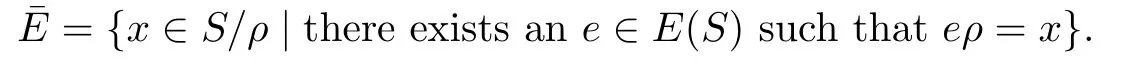
Then,by de finition ofρ,we have

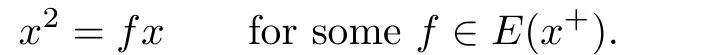
This implies

Henceand so

De finition 1.2[3]A semigroup S is said to be a C-wlpp semigroup if each R∗∗-class of S contains an idempotent and all idempotents of S are central in S.

Theorem 1.1If S is right-e wlpp semigroup,then S/ρ is the maximum homomorphism image of S such that S/ρ is a C-wlpp semigroup.

Proof.Suppose thatSis right-ewlpp semigroup.ThenS/ρis clearly a wlpp semigroup by Lemma 1.5.To prove thatS/ρis aC-wlpp semigroup,we need to show that every idempotent ofS/ρlies in the center ofS/ρ.TakeandThen,there exists ansuch that.Thus,we have

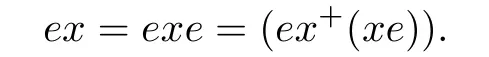
On the other hand,it is clearly that

This implies

Consequently,by the de finition ofthat is,

This proves thatS/ρis aC-wlpp semigroup.

Finally,we show thatρis the smallestC-wlpp congruence onS.Suppose thatτis a congruence onSsuch thatS/τis aC-wlpp semigroup,and letThen

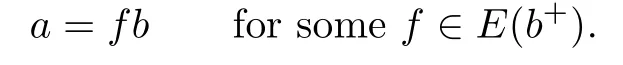
SinceS/ρis aC-wlpp semigroup whose idempotents are central andE(b+)is a left zero band,it follows that

and hence

2 Main Result

In this section,we give a structure theorem of right-ewlpp semigroups.

We first give a new concept.A semigroupSis said to beL-right cancellative,ifthen

Theorem 2.1The following conditions on a semigroup S are equivalent:

(1)S is a right-e wlpp semigroup;

(2)S is a spined product of a C-wlpp semigroup and a left normal band with respect to a semilattice Y;

(3)S is a strong semilattice of L-right cancellative planks.

Proof.(1)⇒(2).LetSbe a right-ewlpp semigroup.Then,by Theorem 1.1,is aC-wlpp semigroup whose idempotents are central inS/ρ.According to Tang[1],can be expressed as a strong semilattiveofL-right cancellative monoidswhereMαareR∗∗-class ofClearly,andSinceE(S)is a left normal band,andEαare left zero bands.Hence,we have a spined product ofandE(S)with respect to the semilatticeY(see[4]),denoted bywhere the multiplication onTis de fined bymnandijare the semigroup products ofm,ninS/ρandi,jinE(S),respectively.To show thatwe consider a mappinggiven by

Firstly we show thatθis surjection.

To show thatθis injective,letforIt is clear thatandHence there exists ansuch thats=ftby the de finition ofρ.Sinceis a left zero band,it follows that

Henceθis an injective mapping.

Finally,we claim thatθis a homomorphism fromStoT.By Lemma 1.3,we have

This prove thatθis an isomorphism.Thus,Sis isomorphic to a spined product of aC-wlpp semigroup and a left normal band.

(2)⇒(3).Suppose thatis a spined product of aC-wlpp semigroupand a left normal bandwith respect to a semilatticeY.Then,for allwithα≥βand,de fine a mappingfromby

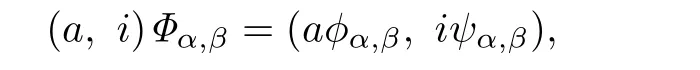
whereϕα,βandψα,βare structure homomorphism forMandE,respectively.

We now show thatΦα,βis a homomorphism.Ifthen

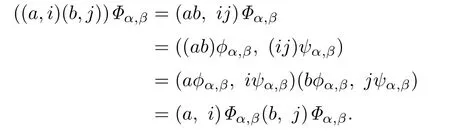
Clearly,Φα,αis an identity mapping onandfor allα,β,γinYwith

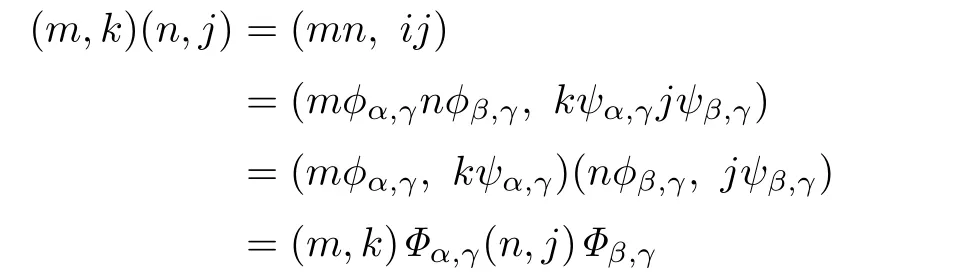
Thus,Sis isomorphic to a strong semilattice ofL-right cancellative planks

(3)⇒(1).Suppose thatis a strong semilative ofL-right cancellative plankswith the structure morphismΦα,β,where we write

We first show that

This prove that

Clearly,

Hence,

Then we claim thatSis a wlpp semigroup.Let.Thenand hence

Finally,we prove that every idempotent ofSis right central.LetandThen there existsuch thatandwe writeThen,andHence,we have

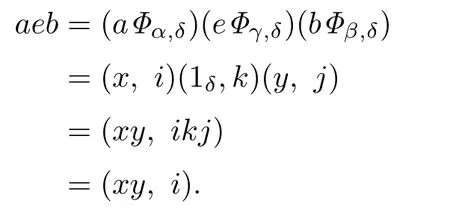
Similarly,we have

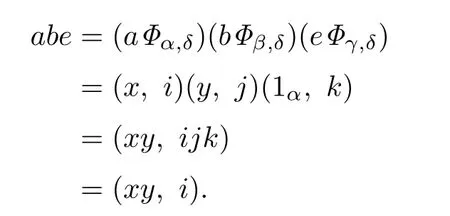
[1]Tang X D.On a theorem ofC-wrpp semigroups.Comm.Algebra,1997,25(5):1499–1504.

[2]Howie J M.Fundamentals of Semigroup Theory,New York:Oxford University Press,1995.

[3]Fountain J B.Abundant semigroups.Proc.London Math.Soc.(3),1982,44(3):103–129.

[4]Howie J M.An Introduction to Semigroup Theory.New York:Academic Press,1976.

tion:08A05

A

1674-5647(2017)03-0274-07

10.13447/j.1674-5647.2017.03.07

date:April 22,2016.

The NSF(11471255)of China,the Scienti fic Research Project(15JK1411)of Education Department of Shaanxi Provincial Government,and the Scienti fic Research Project(17KY02)of College.

E-mail address:chunru123@163.com(Wang C R).